江苏省2024年普通高中学业水平合格性考试数学仿真模拟试卷03(含解析)
文档属性
| 名称 | 江苏省2024年普通高中学业水平合格性考试数学仿真模拟试卷03(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 777.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 19:38:38 | ||
图片预览




文档简介
江苏省2024年普通高中学业水平合格性考试
数学仿真模拟试卷03
选择题(本大题共28题,每小题3分,共计84分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,则( )
A. B. C. D.
2.下列不等式中,解集为的是( )
A. B. C. D.
3.若复数z的共轭复数为,且,则z的虚部为( )
A. B. C. D.2
4.样本101,98,102,100,99的平均数为
A.101 B.100 C.99 D.
5.关于命题,下列说法正确的是( )
A.,且命题是假命题
B.,且命题是真命题
C.,且命题是假命题
D.,且命题是真命题
6.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则( )
A. B. C. D.
7.函数 的定义域是( )
A. B.
C. D.
8.已知函数的最小正周期为,若,把的图象向左平移个单位长度,得到奇函数的图象,则( )
A. B.2 C. D.
9.移动支付技术的进步给人们的生活带来了巨大的便利,很多人出门已经习惯了不带现金,达到“一机在手,天下我有”的境界.某超市某日采用手机支付的老 中 青三个年龄段的顾客共1250人,其比例如图所示,则估计该超市该日采用手机支付的青年人的人数约为( )
A.375 B.680 C.688 D.698
10.从分别写有1,2,3,4,5的5张卡片中任意抽取2张,则抽到的2张卡片上的数字之和是偶数的概率为( )
A. B. C. D.
11.设,,,则( )
A. B. C. D.
12.已知是直线,是两个不同平面,下列命题中的真命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
13.下列函数为奇函数的是( )
A. B. C. D.
14.已知,,则( )
A. B. C. D.
15.下列各角中,与角终边相同的角为( )
A. B. C. D.
16.已知函数在区间上是单调函数,则的取值范围是( )
A. B. C. D.
17.函数在上的最小值为( )
A. B. C. D.
18.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图的面积为( )
A.π B.π C.3π D.4π
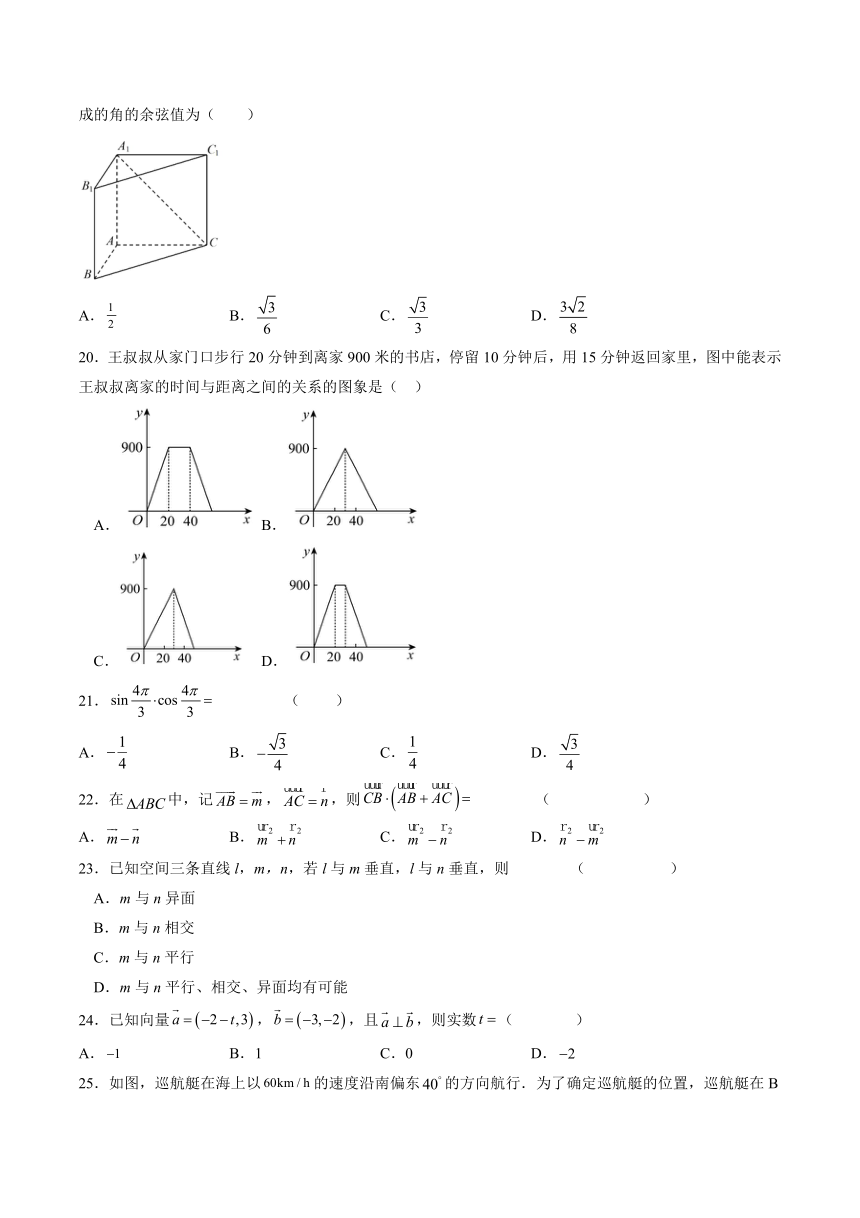
19.如图,在直三棱柱中,若,,,则异面直线与所成的角的余弦值为( )
A. B. C. D.
20.王叔叔从家门口步行20分钟到离家900米的书店,停留10分钟后,用15分钟返回家里,图中能表示王叔叔离家的时间与距离之间的关系的图象是( )
A. B.
C. D.
21. ( )
A. B. C. D.
22.在中,记,,则 ( )
A. B. C. D.
23.已知空间三条直线l,m,n,若l与m垂直,l与n垂直,则 ( )
A.m与n异面
B.m与n相交
C.m与n平行
D.m与n平行、相交、异面均有可能
24.已知向量,,且,则实数( )
A. B.1 C.0 D.
25.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是( )
A. B. C. D.
26.当生物死亡后,它机体内原有的碳14会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.经过9个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前的( )
A. B. C. D.
27.已知一个圆柱的轴截面为正方形,且它的侧面积为,则该圆柱的体积为( )
A. B. C. D.
28.在△ABC中,若A=60°,C=45°,c=,则a等于 ( )
A.1 B. C. D.2
二 解答题:本大题共2小题,共计16分.解答应写出文字说明 证明过程或演算步骤.
29.(本小题满分8分)
如图,在四棱锥中,底面为正方形,平面平面,,,为的中点.
(1)求证:平面;
(2)求四棱锥的体积.
30.(本小题满分8分)
已知函数.
(1)求在上的单调递增区间;
(2)求函数在上的所有零点之和.
选择题(本大题共28题,每小题3分,共计84分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,则( )
A. B. C. D.
1.【答案】B
【解析】,,.故选B.
2.下列不等式中,解集为的是( )
A. B. C. D.
2.【答案】B
【解析】对于A,,故A不符合;对于B,,且开口向上,所以对任意的,都有,故B符合;对于C,得,故C不符合;对于D,由得,故D不符合.故选B.
3.若复数z的共轭复数为,且,则z的虚部为( )
A. B. C. D.2
3.【答案】D
【解析】设复数,a,,则,
即,解得,则,故z的虚部为2.故选D.
4.样本101,98,102,100,99的平均数为
A.101 B.100 C.99 D.
4.【答案】B
【解析】根据平均数的计算公式,直接计算,即可得出结果.【解析】.故选B.
5.关于命题,下列说法正确的是( )
A.,且命题是假命题
B.,且命题是真命题
C.,且命题是假命题
D.,且命题是真命题
5.【答案】A
【解析】由题意得,对于命题,当时,,即命题是真命题,所以命题是假命题.故选A.
6.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则( )
A. B. C. D.
6.【答案】D
【解析】由三角函数的定义得,,,
所以,.故选D.
7.函数 的定义域是( )
A. B.
C. D.
7.【答案】C
【解析】由得.故选C.
8.已知函数的最小正周期为,若,把的图象向左平移个单位长度,得到奇函数的图象,则( )
A. B.2 C. D.
8.【答案】A
【解析】,∵为奇函数,∴,即,∴.又,∴,∵,∴,∴,∴,∴.故选A.
9.移动支付技术的进步给人们的生活带来了巨大的便利,很多人出门已经习惯了不带现金,达到“一机在手,天下我有”的境界.某超市某日采用手机支付的老 中 青三个年龄段的顾客共1250人,其比例如图所示,则估计该超市该日采用手机支付的青年人的人数约为( )
A.375 B.680 C.688 D.698
9.【答案】C
【解析】由扇形统计图可知采用手机支付的青年人所占的比例为,因为采用手机支付的老 中 青三个年龄段的顾客共1250人,所以该日采用手机支付的青年人的人数约为人.故选C.
10.从分别写有1,2,3,4,5的5张卡片中任意抽取2张,则抽到的2张卡片上的数字之和是偶数的概率为( )
A. B. C. D.
10.【答案】B
【解析】1,2,3,4,5的5张卡片中任意抽取2张,有10种情况:
,其中抽到的2张卡片的数字之和是偶数的共4种情况:,所以概率为.故选B.
11.设,,,则( )
A. B. C. D.
11.【答案】A
【解析】,,,所以.故选A.
12.已知是直线,是两个不同平面,下列命题中的真命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.【答案】C
【解析】若,则有,故A错误.若,则或,故B错误.若,则存在直线与平行,所以,故C正确.若,则或,故D错误.故选C.
13.下列函数为奇函数的是( )
A. B. C. D.
13.【答案】A
【解析】对于A:定义域为,且,A正确;对于B:定义域为,且,为偶函数,B错误;对于C:定义域为,且,为偶函数,C错误;对于D:定义域为,且,为偶函数,D错误.故选A.
14.已知,,则( )
A. B. C. D.
14.【答案】C
【解析】由题意,,则.故选C.
15.下列各角中,与角终边相同的角为( )
A. B. C. D.
15.【答案】B
【解析】与角终边相同的角为,,对于A:取,不是整数解,A错误;对于B:取,,B正确;对于C:取,不是整数解,C错误;对于D:取,不是整数解,D错误.故选B.
16.已知函数在区间上是单调函数,则的取值范围是( )
A. B. C. D.
16.【答案】D
【解析】的图象的对称轴为,因为函数在区间上时单调函数,所以或,得或,即的取值范围是.
故选D.
17.函数在上的最小值为( )
A. B. C. D.
17.【答案】B
【解析】函数在上单调递减,其向左平移3个单位可得到,则其在上单调递减,所以函数在上单调递减,即有时取得最小值,且为.故选B.
18.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图的面积为( )
A.π B.π C.3π D.4π
18.【答案】A
【解析】圆锥的侧面展开图是半径为,弧长为2π的扇形,其面积S=l·r=×2π×=π,所以圆锥的侧面展开图的面积为π.
19.如图,在直三棱柱中,若,,,则异面直线与所成的角的余弦值为( )
A. B. C. D.
19.【答案】C
【解析】连接,则,,,因为∥,所以或其补角为异面直线与所成的角,,则异面直线与所成的角的余弦值为.故选C.
20.王叔叔从家门口步行20分钟到离家900米的书店,停留10分钟后,用15分钟返回家里,图中能表示王叔叔离家的时间与距离之间的关系的图象是( )
A. B.
C. D.
20.【答案】D
【解析】由题意0-20分钟,步行到离家900米的书店,离家路程增加到900米,
20-30分钟停留,离家路程不变,30-45分钟返回家,离家路程减少为0米.故选D.
21. ( )
A. B. C. D.
21.【答案】D
【解析】.故选D.
22.在中,记,,则 ( )
A. B. C. D.
22.【答案】C
【解析】.故选C.
23.已知空间三条直线l,m,n,若l与m垂直,l与n垂直,则 ( )
A.m与n异面
B.m与n相交
C.m与n平行
D.m与n平行、相交、异面均有可能
23.D【解析】因为m⊥l,n⊥l,结合长方体模型可知m与n可以相交,也可以异面,还可以平行.故选D.
24.已知向量,,且,则实数( )
A. B.1 C.0 D.
24.C【解析】由题意得:,解得:.故选C.
25.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是( )
A. B. C. D.
25.D【解析】在中,,,
,则,由正弦定理可得,,可得.故选D.
26.当生物死亡后,它机体内原有的碳14会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.经过9个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前的( )
A. B. C. D.
26.C【解析】设生物组织死亡前碳14的含量为1,经过1个半衰期后,死亡生物组织内的碳14的剩余量为,经过n个半衰期后,死亡生物组织内的碳14的剩余为,当时,.故选C.
27.已知一个圆柱的轴截面为正方形,且它的侧面积为,则该圆柱的体积为( )
A. B. C. D.
27.D【解析】设圆柱底面半径为R,高为h,设,解得,∴圆柱的体积为.故选D.
28.在△ABC中,若A=60°,C=45°,c=,则a等于 ( )
A.1 B. C. D.2
28.B【解析】由正弦定理得,a==.故选B.
二 解答题:本大题共2小题,共计16分.解答应写出文字说明 证明过程或演算步骤.
29.(本小题满分8分)
如图,在四棱锥中,底面为正方形,平面平面,,,为的中点.
(1)求证:平面;
(2)求四棱锥的体积.
29.【解析】(1),为的中点,
故,(2分)
又平面平面,
平面平面,
平面,
故平面.(4分)
(2),,
故,.(6分)
故.(8分)
30.(本小题满分8分)
已知函数.
(1)求在上的单调递增区间;
(2)求函数在上的所有零点之和.
30.【解析】(1)
.(2分)
的单调增区间是 ,
又 ,
令 有 ,即 ,
令 有 ,即 ,
所以 在 上的增区间为 和 .(4分)
(2)由题意: ,即 .
或者 ,
又 , ,(6分)
k可取-2,-1,0,1,
对应的零点分别为:, 其和为 .
综上, 在 上的单调增区间为 和 ,
在 的所有零点之和为 .(8分)
数学仿真模拟试卷03
选择题(本大题共28题,每小题3分,共计84分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,则( )
A. B. C. D.
2.下列不等式中,解集为的是( )
A. B. C. D.
3.若复数z的共轭复数为,且,则z的虚部为( )
A. B. C. D.2
4.样本101,98,102,100,99的平均数为
A.101 B.100 C.99 D.
5.关于命题,下列说法正确的是( )
A.,且命题是假命题
B.,且命题是真命题
C.,且命题是假命题
D.,且命题是真命题
6.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则( )
A. B. C. D.
7.函数 的定义域是( )
A. B.
C. D.
8.已知函数的最小正周期为,若,把的图象向左平移个单位长度,得到奇函数的图象,则( )
A. B.2 C. D.
9.移动支付技术的进步给人们的生活带来了巨大的便利,很多人出门已经习惯了不带现金,达到“一机在手,天下我有”的境界.某超市某日采用手机支付的老 中 青三个年龄段的顾客共1250人,其比例如图所示,则估计该超市该日采用手机支付的青年人的人数约为( )
A.375 B.680 C.688 D.698
10.从分别写有1,2,3,4,5的5张卡片中任意抽取2张,则抽到的2张卡片上的数字之和是偶数的概率为( )
A. B. C. D.
11.设,,,则( )
A. B. C. D.
12.已知是直线,是两个不同平面,下列命题中的真命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
13.下列函数为奇函数的是( )
A. B. C. D.
14.已知,,则( )
A. B. C. D.
15.下列各角中,与角终边相同的角为( )
A. B. C. D.
16.已知函数在区间上是单调函数,则的取值范围是( )
A. B. C. D.
17.函数在上的最小值为( )
A. B. C. D.
18.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图的面积为( )
A.π B.π C.3π D.4π
19.如图,在直三棱柱中,若,,,则异面直线与所成的角的余弦值为( )
A. B. C. D.
20.王叔叔从家门口步行20分钟到离家900米的书店,停留10分钟后,用15分钟返回家里,图中能表示王叔叔离家的时间与距离之间的关系的图象是( )
A. B.
C. D.
21. ( )
A. B. C. D.
22.在中,记,,则 ( )
A. B. C. D.
23.已知空间三条直线l,m,n,若l与m垂直,l与n垂直,则 ( )
A.m与n异面
B.m与n相交
C.m与n平行
D.m与n平行、相交、异面均有可能
24.已知向量,,且,则实数( )
A. B.1 C.0 D.
25.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是( )
A. B. C. D.
26.当生物死亡后,它机体内原有的碳14会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.经过9个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前的( )
A. B. C. D.
27.已知一个圆柱的轴截面为正方形,且它的侧面积为,则该圆柱的体积为( )
A. B. C. D.
28.在△ABC中,若A=60°,C=45°,c=,则a等于 ( )
A.1 B. C. D.2
二 解答题:本大题共2小题,共计16分.解答应写出文字说明 证明过程或演算步骤.
29.(本小题满分8分)
如图,在四棱锥中,底面为正方形,平面平面,,,为的中点.
(1)求证:平面;
(2)求四棱锥的体积.
30.(本小题满分8分)
已知函数.
(1)求在上的单调递增区间;
(2)求函数在上的所有零点之和.
选择题(本大题共28题,每小题3分,共计84分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,则( )
A. B. C. D.
1.【答案】B
【解析】,,.故选B.
2.下列不等式中,解集为的是( )
A. B. C. D.
2.【答案】B
【解析】对于A,,故A不符合;对于B,,且开口向上,所以对任意的,都有,故B符合;对于C,得,故C不符合;对于D,由得,故D不符合.故选B.
3.若复数z的共轭复数为,且,则z的虚部为( )
A. B. C. D.2
3.【答案】D
【解析】设复数,a,,则,
即,解得,则,故z的虚部为2.故选D.
4.样本101,98,102,100,99的平均数为
A.101 B.100 C.99 D.
4.【答案】B
【解析】根据平均数的计算公式,直接计算,即可得出结果.【解析】.故选B.
5.关于命题,下列说法正确的是( )
A.,且命题是假命题
B.,且命题是真命题
C.,且命题是假命题
D.,且命题是真命题
5.【答案】A
【解析】由题意得,对于命题,当时,,即命题是真命题,所以命题是假命题.故选A.
6.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则( )
A. B. C. D.
6.【答案】D
【解析】由三角函数的定义得,,,
所以,.故选D.
7.函数 的定义域是( )
A. B.
C. D.
7.【答案】C
【解析】由得.故选C.
8.已知函数的最小正周期为,若,把的图象向左平移个单位长度,得到奇函数的图象,则( )
A. B.2 C. D.
8.【答案】A
【解析】,∵为奇函数,∴,即,∴.又,∴,∵,∴,∴,∴,∴.故选A.
9.移动支付技术的进步给人们的生活带来了巨大的便利,很多人出门已经习惯了不带现金,达到“一机在手,天下我有”的境界.某超市某日采用手机支付的老 中 青三个年龄段的顾客共1250人,其比例如图所示,则估计该超市该日采用手机支付的青年人的人数约为( )
A.375 B.680 C.688 D.698
9.【答案】C
【解析】由扇形统计图可知采用手机支付的青年人所占的比例为,因为采用手机支付的老 中 青三个年龄段的顾客共1250人,所以该日采用手机支付的青年人的人数约为人.故选C.
10.从分别写有1,2,3,4,5的5张卡片中任意抽取2张,则抽到的2张卡片上的数字之和是偶数的概率为( )
A. B. C. D.
10.【答案】B
【解析】1,2,3,4,5的5张卡片中任意抽取2张,有10种情况:
,其中抽到的2张卡片的数字之和是偶数的共4种情况:,所以概率为.故选B.
11.设,,,则( )
A. B. C. D.
11.【答案】A
【解析】,,,所以.故选A.
12.已知是直线,是两个不同平面,下列命题中的真命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.【答案】C
【解析】若,则有,故A错误.若,则或,故B错误.若,则存在直线与平行,所以,故C正确.若,则或,故D错误.故选C.
13.下列函数为奇函数的是( )
A. B. C. D.
13.【答案】A
【解析】对于A:定义域为,且,A正确;对于B:定义域为,且,为偶函数,B错误;对于C:定义域为,且,为偶函数,C错误;对于D:定义域为,且,为偶函数,D错误.故选A.
14.已知,,则( )
A. B. C. D.
14.【答案】C
【解析】由题意,,则.故选C.
15.下列各角中,与角终边相同的角为( )
A. B. C. D.
15.【答案】B
【解析】与角终边相同的角为,,对于A:取,不是整数解,A错误;对于B:取,,B正确;对于C:取,不是整数解,C错误;对于D:取,不是整数解,D错误.故选B.
16.已知函数在区间上是单调函数,则的取值范围是( )
A. B. C. D.
16.【答案】D
【解析】的图象的对称轴为,因为函数在区间上时单调函数,所以或,得或,即的取值范围是.
故选D.
17.函数在上的最小值为( )
A. B. C. D.
17.【答案】B
【解析】函数在上单调递减,其向左平移3个单位可得到,则其在上单调递减,所以函数在上单调递减,即有时取得最小值,且为.故选B.
18.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图的面积为( )
A.π B.π C.3π D.4π
18.【答案】A
【解析】圆锥的侧面展开图是半径为,弧长为2π的扇形,其面积S=l·r=×2π×=π,所以圆锥的侧面展开图的面积为π.
19.如图,在直三棱柱中,若,,,则异面直线与所成的角的余弦值为( )
A. B. C. D.
19.【答案】C
【解析】连接,则,,,因为∥,所以或其补角为异面直线与所成的角,,则异面直线与所成的角的余弦值为.故选C.
20.王叔叔从家门口步行20分钟到离家900米的书店,停留10分钟后,用15分钟返回家里,图中能表示王叔叔离家的时间与距离之间的关系的图象是( )
A. B.
C. D.
20.【答案】D
【解析】由题意0-20分钟,步行到离家900米的书店,离家路程增加到900米,
20-30分钟停留,离家路程不变,30-45分钟返回家,离家路程减少为0米.故选D.
21. ( )
A. B. C. D.
21.【答案】D
【解析】.故选D.
22.在中,记,,则 ( )
A. B. C. D.
22.【答案】C
【解析】.故选C.
23.已知空间三条直线l,m,n,若l与m垂直,l与n垂直,则 ( )
A.m与n异面
B.m与n相交
C.m与n平行
D.m与n平行、相交、异面均有可能
23.D【解析】因为m⊥l,n⊥l,结合长方体模型可知m与n可以相交,也可以异面,还可以平行.故选D.
24.已知向量,,且,则实数( )
A. B.1 C.0 D.
24.C【解析】由题意得:,解得:.故选C.
25.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是( )
A. B. C. D.
25.D【解析】在中,,,
,则,由正弦定理可得,,可得.故选D.
26.当生物死亡后,它机体内原有的碳14会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.经过9个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前的( )
A. B. C. D.
26.C【解析】设生物组织死亡前碳14的含量为1,经过1个半衰期后,死亡生物组织内的碳14的剩余量为,经过n个半衰期后,死亡生物组织内的碳14的剩余为,当时,.故选C.
27.已知一个圆柱的轴截面为正方形,且它的侧面积为,则该圆柱的体积为( )
A. B. C. D.
27.D【解析】设圆柱底面半径为R,高为h,设,解得,∴圆柱的体积为.故选D.
28.在△ABC中,若A=60°,C=45°,c=,则a等于 ( )
A.1 B. C. D.2
28.B【解析】由正弦定理得,a==.故选B.
二 解答题:本大题共2小题,共计16分.解答应写出文字说明 证明过程或演算步骤.
29.(本小题满分8分)
如图,在四棱锥中,底面为正方形,平面平面,,,为的中点.
(1)求证:平面;
(2)求四棱锥的体积.
29.【解析】(1),为的中点,
故,(2分)
又平面平面,
平面平面,
平面,
故平面.(4分)
(2),,
故,.(6分)
故.(8分)
30.(本小题满分8分)
已知函数.
(1)求在上的单调递增区间;
(2)求函数在上的所有零点之和.
30.【解析】(1)
.(2分)
的单调增区间是 ,
又 ,
令 有 ,即 ,
令 有 ,即 ,
所以 在 上的增区间为 和 .(4分)
(2)由题意: ,即 .
或者 ,
又 , ,(6分)
k可取-2,-1,0,1,
对应的零点分别为:, 其和为 .
综上, 在 上的单调增区间为 和 ,
在 的所有零点之和为 .(8分)
同课章节目录
