数学人教A版(2019)选择性必修第二册5.1.2导数的几何意义 课件(共41张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.1.2导数的几何意义 课件(共41张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 20:37:41 | ||
图片预览









文档简介
(共41张PPT)
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
5.1 导数的概念及其意义
5.1.2 导数的概念及其几何意义
教学目标
1.根据导数的几何意义,会求曲线上某点处的切线方程
2.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
3.培养学生数学抽象及直观想象的核心素养,提升数学运算核心素养.
01
复习导入
复习导入
导数的概念
如果当时,平均变化率无限趋近于一个确定的值,即有极限,则称在处可导,并把这个确定的值叫做在处的导数(也称为瞬时变化率),记作或,
即
导数是平均变化率的极限,是瞬时变化率的数学表达.
复习导入
(1)求增量
(2)求平均变化率
(3)求极限
求某点处导数值的步骤
一差、二比、三极限
02
导数的几何意义
新知探究
我们知道,导数表示函数在处的瞬时变化率,反映了函数在附近的变化情况.
探究:导数的几何意义是什么?
新知探究
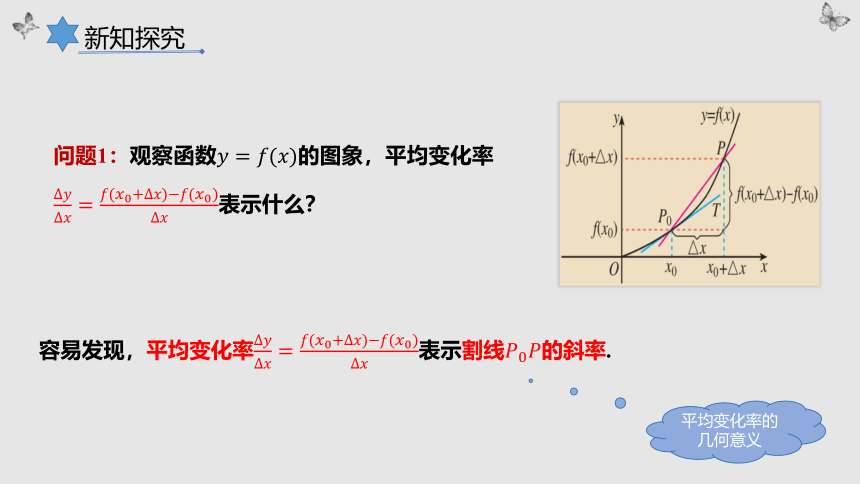
问题1:观察函数的图象,平均变化率表示什么?
容易发现,平均变化率表示割线的斜率.
平均变化率的几何意义
新知探究
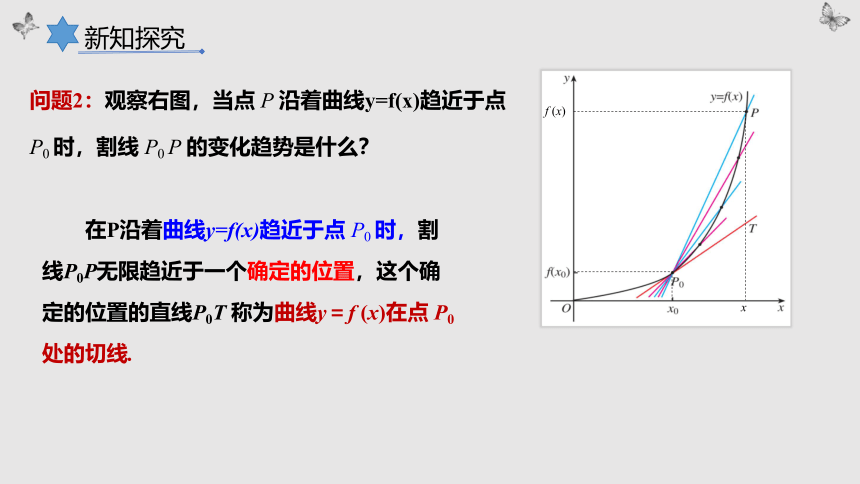
问题2:观察右图,当点 P 沿着曲线y=f(x)趋近于点 P0 时,割线 P0 P 的变化趋势是什么?
x
f (x)
在P沿着曲线y=f(x)趋近于点 P0 时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
新知探究
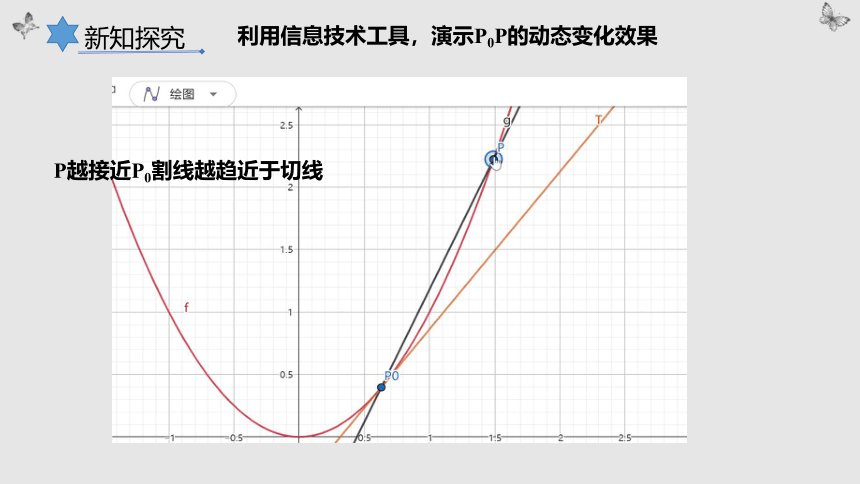
利用信息技术工具,演示P0P的动态变化效果
P越接近P0割线越趋近于切线
新知探究
问题3:瞬时变化率表示什么?
割线的斜率.记,当点沿着曲线无限趋近于点时,即当时,无限趋近于函数在处的导数.
因此,函数在处的导数就是切线的斜率,即
. 这就是导数的几何意义.
新知探究
新知探究
新知探究
新知探究
方法总结
求曲线上一点处的切线方程可按以下步骤进行:(1)求出该点的坐标.(2)求出函数在该点处的导数,即曲线在该点处的切线的斜率.(3)利用点斜式写出切线方程.
新知探究
练习:求曲线在点处的切线方程.
解:由导数的几何意义,曲线在点处的切线的斜率就等于函数在点处的导数.
而,
故曲线在点处的切线方程为,整理得.
新知探究
A
新知探究
新知探究
方法总结
新知探究
新知探究
例3.已知直线和曲线相切,求的值和切点的坐标.
解:设直线与曲线相切于点,则
.
由题意可知,直线的斜率,即,解得或,
∴切点的坐标为或.
新知探究
求切点坐标的4个步骤
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
新知探究
l
练习:直线和曲线相切,则的值为_________,切点坐标为___________.
则解得或.
解:设直线与曲线的切点为,
∵
当时,,
又在直线上,
将,代入得,与已知条件矛盾,舍去.
新知探究
l
03
函数的单调性与导数的关系
新知探究
l
分析:我们用曲线在处的切线斜率,刻画曲线在上述三个时刻附近的变化情况.
探究:右图是高台跳水运动中运动员的重心相对于水面的高度随时间变化的函数的图象.根据图象,回答下列问题.
l
问题1:比较曲线在t=t0附近的变化情况.
(1)当时,曲线在处的切线平行于轴,.这时,在附近曲线比较平坦,几乎没有升降.
新知探究
l
(2)当时,曲线在处的切线的斜率.这时,在附近曲线下降,即函数在附近单调递减.
问题2:比较曲线在t=t1附近的变化情况.
问题3:比较曲线在t=t2附近的变化情况.
(3)当时,曲线在处的切线平行于轴,.这时,在附近曲线下降,即函数在附近也单调递减.
新知探究
l
函数的单调性与导数的关系(1)若f′(x0)=0,则函数在x=x0处切线的斜率k=____;(2)若f′(x0)>0,则函数在x=x0处切线的斜率k____0,且函数在x=x0附近________________,f′(x0)越大,说明函数图象变化得越快;
0
>
单调递增
(3)若f′(x0)<0,则函数在x=x0处切线的斜率k____0,且函数在x=x0附近_________,|f′(x0)|越大,说明函数图象变化得越快.
<
单调递减
新知探究
l
A
新知探究
l
新知探究
l
新知探究
l
A
D
新知探究
l
04
导函数
新知探究
l
导函数从求函数y=f(x)在x=x0处导数的过程可以看出,当x=x0时,f′(x0)是一个唯一确定的数.
这样,当x变化时,y=f′(x)就是x的函数,我们称它为y=f(x)的________ (简称导数).y=f(x)的导函数记作______或_____,即f′(x)=y′ =____________________________
导函数
f′(x)
y′
f′(x)=y′=
新知探究
l
(3)函数在点 x0 处的导数 f ′(x0)就是导函数 f ′(x) 在 x = x0 处的函数值,这也是 求函数在点 x0 处的导数的方法之一。
问题:函数在点x =x0处的导数f ′(x0)、导函数 y = f ′(x)、导数之间有什么区别与联系呢?
(1)函数在一点x0处的导数 f ′(x0) ,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
(2)函数的导数,是指某一区间内任意点x而言的, 就是函数 f (x)的导函数 f ′(x),它是一个变量。
新知探究
l
新知探究
l
新知探究
l
方法总结
05
课堂小结
课堂小结
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
5.1 导数的概念及其意义
5.1.2 导数的概念及其几何意义
教学目标
1.根据导数的几何意义,会求曲线上某点处的切线方程
2.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
3.培养学生数学抽象及直观想象的核心素养,提升数学运算核心素养.
01
复习导入
复习导入
导数的概念
如果当时,平均变化率无限趋近于一个确定的值,即有极限,则称在处可导,并把这个确定的值叫做在处的导数(也称为瞬时变化率),记作或,
即
导数是平均变化率的极限,是瞬时变化率的数学表达.
复习导入
(1)求增量
(2)求平均变化率
(3)求极限
求某点处导数值的步骤
一差、二比、三极限
02
导数的几何意义
新知探究
我们知道,导数表示函数在处的瞬时变化率,反映了函数在附近的变化情况.
探究:导数的几何意义是什么?
新知探究
问题1:观察函数的图象,平均变化率表示什么?
容易发现,平均变化率表示割线的斜率.
平均变化率的几何意义
新知探究
问题2:观察右图,当点 P 沿着曲线y=f(x)趋近于点 P0 时,割线 P0 P 的变化趋势是什么?
x
f (x)
在P沿着曲线y=f(x)趋近于点 P0 时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
新知探究
利用信息技术工具,演示P0P的动态变化效果
P越接近P0割线越趋近于切线
新知探究
问题3:瞬时变化率表示什么?
割线的斜率.记,当点沿着曲线无限趋近于点时,即当时,无限趋近于函数在处的导数.
因此,函数在处的导数就是切线的斜率,即
. 这就是导数的几何意义.
新知探究
新知探究
新知探究
新知探究
方法总结
求曲线上一点处的切线方程可按以下步骤进行:(1)求出该点的坐标.(2)求出函数在该点处的导数,即曲线在该点处的切线的斜率.(3)利用点斜式写出切线方程.
新知探究
练习:求曲线在点处的切线方程.
解:由导数的几何意义,曲线在点处的切线的斜率就等于函数在点处的导数.
而,
故曲线在点处的切线方程为,整理得.
新知探究
A
新知探究
新知探究
方法总结
新知探究
新知探究
例3.已知直线和曲线相切,求的值和切点的坐标.
解:设直线与曲线相切于点,则
.
由题意可知,直线的斜率,即,解得或,
∴切点的坐标为或.
新知探究
求切点坐标的4个步骤
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
新知探究
l
练习:直线和曲线相切,则的值为_________,切点坐标为___________.
则解得或.
解:设直线与曲线的切点为,
∵
当时,,
又在直线上,
将,代入得,与已知条件矛盾,舍去.
新知探究
l
03
函数的单调性与导数的关系
新知探究
l
分析:我们用曲线在处的切线斜率,刻画曲线在上述三个时刻附近的变化情况.
探究:右图是高台跳水运动中运动员的重心相对于水面的高度随时间变化的函数的图象.根据图象,回答下列问题.
l
问题1:比较曲线在t=t0附近的变化情况.
(1)当时,曲线在处的切线平行于轴,.这时,在附近曲线比较平坦,几乎没有升降.
新知探究
l
(2)当时,曲线在处的切线的斜率.这时,在附近曲线下降,即函数在附近单调递减.
问题2:比较曲线在t=t1附近的变化情况.
问题3:比较曲线在t=t2附近的变化情况.
(3)当时,曲线在处的切线平行于轴,.这时,在附近曲线下降,即函数在附近也单调递减.
新知探究
l
函数的单调性与导数的关系(1)若f′(x0)=0,则函数在x=x0处切线的斜率k=____;(2)若f′(x0)>0,则函数在x=x0处切线的斜率k____0,且函数在x=x0附近________________,f′(x0)越大,说明函数图象变化得越快;
0
>
单调递增
(3)若f′(x0)<0,则函数在x=x0处切线的斜率k____0,且函数在x=x0附近_________,|f′(x0)|越大,说明函数图象变化得越快.
<
单调递减
新知探究
l
A
新知探究
l
新知探究
l
新知探究
l
A
D
新知探究
l
04
导函数
新知探究
l
导函数从求函数y=f(x)在x=x0处导数的过程可以看出,当x=x0时,f′(x0)是一个唯一确定的数.
这样,当x变化时,y=f′(x)就是x的函数,我们称它为y=f(x)的________ (简称导数).y=f(x)的导函数记作______或_____,即f′(x)=y′ =____________________________
导函数
f′(x)
y′
f′(x)=y′=
新知探究
l
(3)函数在点 x0 处的导数 f ′(x0)就是导函数 f ′(x) 在 x = x0 处的函数值,这也是 求函数在点 x0 处的导数的方法之一。
问题:函数在点x =x0处的导数f ′(x0)、导函数 y = f ′(x)、导数之间有什么区别与联系呢?
(1)函数在一点x0处的导数 f ′(x0) ,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
(2)函数的导数,是指某一区间内任意点x而言的, 就是函数 f (x)的导函数 f ′(x),它是一个变量。
新知探究
l
新知探究
l
新知探究
l
方法总结
05
课堂小结
课堂小结
