物理人教版(2019)选择性必修第一册1.3动量守恒定律(共20张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.3动量守恒定律(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-22 18:27:39 | ||
图片预览






文档简介
(共20张PPT)
复习
一、动量P
1.定义式:
2.性质:
P = mv
矢量。其方向与即时速度的方向相同
二、冲量I
1.定义式:
2.性质:
矢量。恒力冲量的方向与力的方向相同
I=Ft --恒力冲量的计算
三、动量定理:
动量守恒定律
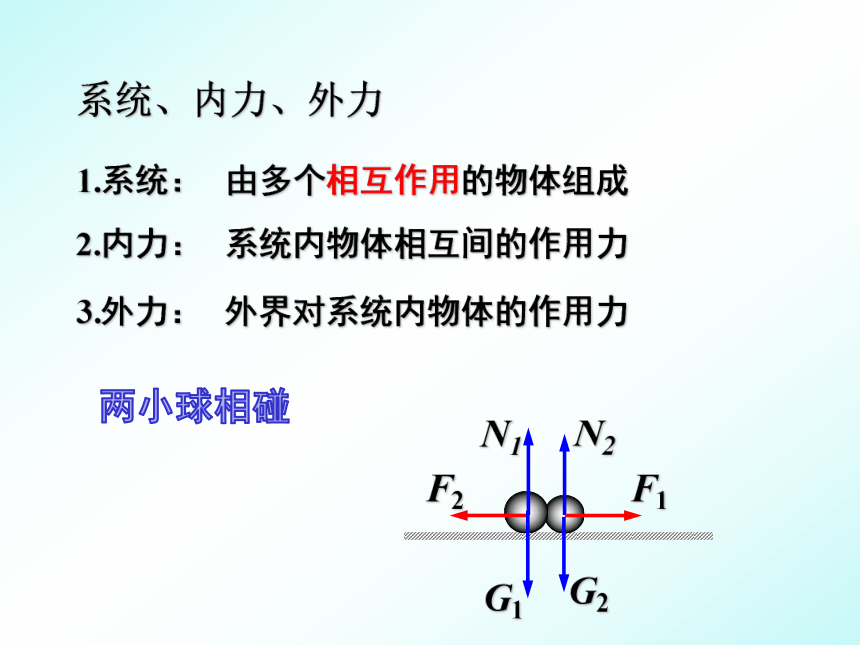
系统、内力、外力
2.内力:
1.系统:
3.外力:
由多个相互作用的物体组成
系统内物体相互间的作用力
外界对系统内物体的作用力
F1
F2
N1
N2
G1
G2
两小球相碰
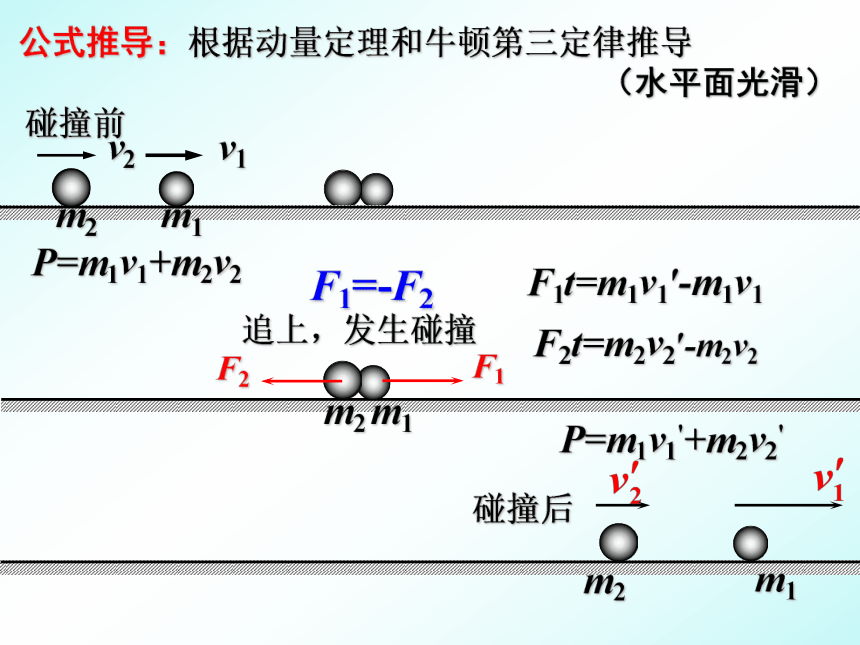
根据动量定理和牛顿第三定律推导
m1
m2
v2
v1
m1
m2
追上,发生碰撞
碰撞前
m1
m2
碰撞后
F1
F2
F1=-F2
公式推导:
F1t=m1v1′-m1v1
F2t=m2v2′-m2v2
(水平面光滑)
P=m1v1+m2v2
P=m1v1'+m2v2'
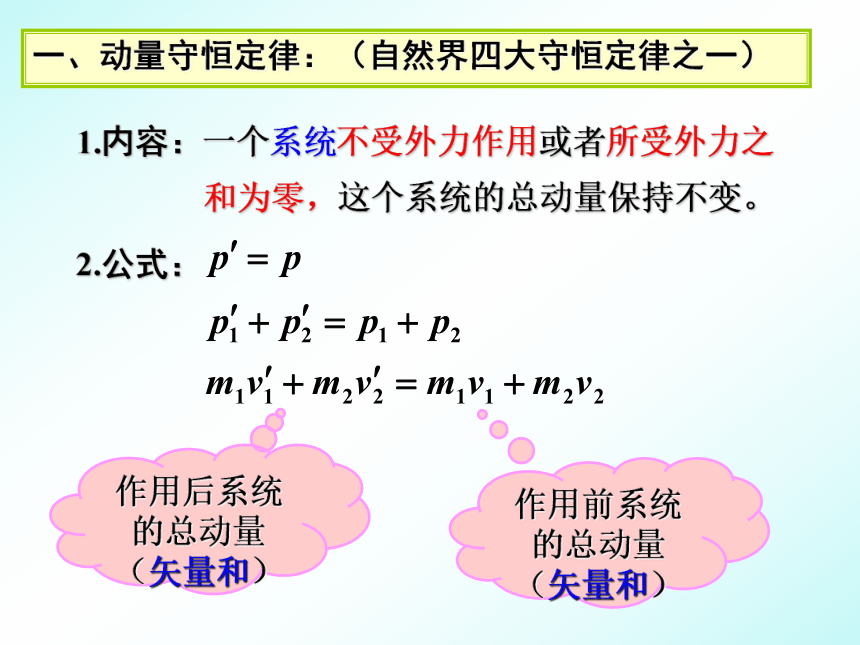
一、动量守恒定律:(自然界四大守恒定律之一)
2.公式:
1.内容:一个系统不受外力作用或者所受外力之
和为零,这个系统的总动量保持不变。
作用后系统的总动量(矢量和)
作用前系统的总动量(矢量和)
①系统不受外力作用
②系统受外力作用,但外力之和为0
③系统受外力作用,但F外 F内,
例如:碰撞、反冲、爆炸等
④在某个方向上的外力之和为0
①两个物体或n个物体组成的系统; ②正碰、斜碰; ③宏观(大至天体)、微观(小至微观粒子); ④恒力作用、变力作用; ⑤短过程、长过程; ⑥任何性质的力 。(了解的力、不了解的力)
3.守恒条件:
4.动量守恒定律的适用范围:
质量m1=10g小球在光滑水平面上以v1=30cm/s速率向右运动,恰遇上质量m2=50g的小球以v2=10cm/s的速率向左运动,碰撞后小球m2恰好静止,那么碰撞后小球m1的速度大小是多大?方向如何?
m1
m2
v2
v1
例题:
解题思路
①选择研究系统,确定研究过程
②分析受力情况,判断动量是否守恒
③选取正方向
④确定始、末状态的动量(用带正负号的数表示)
⑤列具体的动量守恒方程
⑥求解
只讨论一条直线上的情况
练习:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
v1
m1
m2
碰前系统的总动量:
碰后系统的总动量:
说明:本题只有一个方向,所以不用选取正方向了。
质量m1=2kg ,m2=5kg的两静止小车压缩一条轻质弹簧后放在光滑的水平面,放手后让小车弹开今测得m2受到的冲量是10N·s。则
①两小车及弹簧组成的系统动量是否守恒?
②此过程中,m1的动量变化为多少
③弹开后,两小车的总动量为多少?
④弹开后,两车的速度大小之比?
m2
m1
练习:
练习:一枚在空中飞行的火箭,质量为m,在某点的速度为v,方向水平,燃料即将耗尽。火箭在该点突然爆炸成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
以向右为正方向
爆炸前:
爆炸后:
P =mv
P = -m1v1+(m-m1)v2
m1
m-m1
v1
v2
练习:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
v1
m1
m2
碰前系统的总动量:
碰后系统的总动量:
说明:本题只有一个方向,所以不用选取正方向了。
质量m1=2kg ,m2=5kg的两静止小车压缩一条轻质弹簧后放在光滑的水平面,放手后让小车弹开今测得m2受到的冲量是10N·s。则
①两小车及弹簧组成的系统动量是否守恒?
②此过程中,m1的动量变化为多少
③弹开后,两小车的总动量为多少?
④弹开后,两车的速度大小之比?
m2
m1
1.讨论动量守恒的基本条件
若水平地面不光滑,与两车的动摩擦因数μ相同,讨论m1=m2和m1≠m2两种情况下系统的动量是否守恒。
(1)m1=m2时,系统动量是多少?
(2)m1≠m2时,两车运动情况可能是怎样的?
一枚在空中飞行的火箭,质量为m,在某点的速度为v,方向水平,燃料即将耗尽。火箭在该点突然爆炸成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
以向右为正方向
爆炸前:
爆炸后:
P =mv
P = -m1v1+(m-m1)v2
m1
m-m1
v1
v2
2.学习设置正方向,变一维矢量运算为代数运算
v0
①子弹入射过程时间极短,
认为原地发生,悬线无摆动
摆长:沙袋重心到悬点距离
mv0=(m+m1)v
动量守恒:
②系统共速后,由于绳的作用
做圆弧运动
机械能守恒:
?
h=l(1-cosθ)
3.明确研究对象系统,研究过程
受到的外力有:重力支持力
(此时弹簧没来得及形变,弹力为零)
重力和支持力的合力等于零,
所以系统的动量守恒:
机械能守恒吗?产生的热量:
A
B
m
M
子弹入射木块的过程中,子弹和木块组成的系统动量守恒吗?机械能守恒吗?
水平面光滑
思考题:
子弹、木块和弹簧组成系统入射过程时间极短
mv=(M+m)v共
vt=0
思考题:压缩过程:子弹、木块以及弹簧组成的系统,动量守恒吗?机械能守恒吗?能否求出弹簧储存的最大弹性势能?
v
思考题:光滑的水平地面上停着一辆质量为M,长为L小车,质量为m的滑块以速度v滑上小车,最后停在小车上,小车与滑块组成的系统,动量守恒吗?机械能守恒吗?
4.动量守恒定律是对同一个惯性参照系成立的
同步P7/4
mv=(M+m)v共
练习:如图所示,物体A静止在光滑的水平面上,A的左边固定有轻质弹簧,与A质量相等的物体B 以速度v向A运动并与弹簧发生碰撞,A、B始终沿同一直线运动,则A、B组成的系统动能损失最大的时刻是
A.A开始运动时 B.A的速度等于v时
C.B的速度等于零时
D.A和B的速度相等
D.A和B的速度相等
A
B
v
即弹簧储存的弹性势能最大
复习
一、动量P
1.定义式:
2.性质:
P = mv
矢量。其方向与即时速度的方向相同
二、冲量I
1.定义式:
2.性质:
矢量。恒力冲量的方向与力的方向相同
I=Ft --恒力冲量的计算
三、动量定理:
动量守恒定律
系统、内力、外力
2.内力:
1.系统:
3.外力:
由多个相互作用的物体组成
系统内物体相互间的作用力
外界对系统内物体的作用力
F1
F2
N1
N2
G1
G2
两小球相碰
根据动量定理和牛顿第三定律推导
m1
m2
v2
v1
m1
m2
追上,发生碰撞
碰撞前
m1
m2
碰撞后
F1
F2
F1=-F2
公式推导:
F1t=m1v1′-m1v1
F2t=m2v2′-m2v2
(水平面光滑)
P=m1v1+m2v2
P=m1v1'+m2v2'
一、动量守恒定律:(自然界四大守恒定律之一)
2.公式:
1.内容:一个系统不受外力作用或者所受外力之
和为零,这个系统的总动量保持不变。
作用后系统的总动量(矢量和)
作用前系统的总动量(矢量和)
①系统不受外力作用
②系统受外力作用,但外力之和为0
③系统受外力作用,但F外 F内,
例如:碰撞、反冲、爆炸等
④在某个方向上的外力之和为0
①两个物体或n个物体组成的系统; ②正碰、斜碰; ③宏观(大至天体)、微观(小至微观粒子); ④恒力作用、变力作用; ⑤短过程、长过程; ⑥任何性质的力 。(了解的力、不了解的力)
3.守恒条件:
4.动量守恒定律的适用范围:
质量m1=10g小球在光滑水平面上以v1=30cm/s速率向右运动,恰遇上质量m2=50g的小球以v2=10cm/s的速率向左运动,碰撞后小球m2恰好静止,那么碰撞后小球m1的速度大小是多大?方向如何?
m1
m2
v2
v1
例题:
解题思路
①选择研究系统,确定研究过程
②分析受力情况,判断动量是否守恒
③选取正方向
④确定始、末状态的动量(用带正负号的数表示)
⑤列具体的动量守恒方程
⑥求解
只讨论一条直线上的情况
练习:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
v1
m1
m2
碰前系统的总动量:
碰后系统的总动量:
说明:本题只有一个方向,所以不用选取正方向了。
质量m1=2kg ,m2=5kg的两静止小车压缩一条轻质弹簧后放在光滑的水平面,放手后让小车弹开今测得m2受到的冲量是10N·s。则
①两小车及弹簧组成的系统动量是否守恒?
②此过程中,m1的动量变化为多少
③弹开后,两小车的总动量为多少?
④弹开后,两车的速度大小之比?
m2
m1
练习:
练习:一枚在空中飞行的火箭,质量为m,在某点的速度为v,方向水平,燃料即将耗尽。火箭在该点突然爆炸成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
以向右为正方向
爆炸前:
爆炸后:
P =mv
P = -m1v1+(m-m1)v2
m1
m-m1
v1
v2
练习:在列车编组站里,一辆m1=1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
v1
m1
m2
碰前系统的总动量:
碰后系统的总动量:
说明:本题只有一个方向,所以不用选取正方向了。
质量m1=2kg ,m2=5kg的两静止小车压缩一条轻质弹簧后放在光滑的水平面,放手后让小车弹开今测得m2受到的冲量是10N·s。则
①两小车及弹簧组成的系统动量是否守恒?
②此过程中,m1的动量变化为多少
③弹开后,两小车的总动量为多少?
④弹开后,两车的速度大小之比?
m2
m1
1.讨论动量守恒的基本条件
若水平地面不光滑,与两车的动摩擦因数μ相同,讨论m1=m2和m1≠m2两种情况下系统的动量是否守恒。
(1)m1=m2时,系统动量是多少?
(2)m1≠m2时,两车运动情况可能是怎样的?
一枚在空中飞行的火箭,质量为m,在某点的速度为v,方向水平,燃料即将耗尽。火箭在该点突然爆炸成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
以向右为正方向
爆炸前:
爆炸后:
P =mv
P = -m1v1+(m-m1)v2
m1
m-m1
v1
v2
2.学习设置正方向,变一维矢量运算为代数运算
v0
①子弹入射过程时间极短,
认为原地发生,悬线无摆动
摆长:沙袋重心到悬点距离
mv0=(m+m1)v
动量守恒:
②系统共速后,由于绳的作用
做圆弧运动
机械能守恒:
?
h=l(1-cosθ)
3.明确研究对象系统,研究过程
受到的外力有:重力支持力
(此时弹簧没来得及形变,弹力为零)
重力和支持力的合力等于零,
所以系统的动量守恒:
机械能守恒吗?产生的热量:
A
B
m
M
子弹入射木块的过程中,子弹和木块组成的系统动量守恒吗?机械能守恒吗?
水平面光滑
思考题:
子弹、木块和弹簧组成系统入射过程时间极短
mv=(M+m)v共
vt=0
思考题:压缩过程:子弹、木块以及弹簧组成的系统,动量守恒吗?机械能守恒吗?能否求出弹簧储存的最大弹性势能?
v
思考题:光滑的水平地面上停着一辆质量为M,长为L小车,质量为m的滑块以速度v滑上小车,最后停在小车上,小车与滑块组成的系统,动量守恒吗?机械能守恒吗?
4.动量守恒定律是对同一个惯性参照系成立的
同步P7/4
mv=(M+m)v共
练习:如图所示,物体A静止在光滑的水平面上,A的左边固定有轻质弹簧,与A质量相等的物体B 以速度v向A运动并与弹簧发生碰撞,A、B始终沿同一直线运动,则A、B组成的系统动能损失最大的时刻是
A.A开始运动时 B.A的速度等于v时
C.B的速度等于零时
D.A和B的速度相等
D.A和B的速度相等
A
B
v
即弹簧储存的弹性势能最大
