1.2.3 绝对值课件 (共18张PPT)湘教版七年级数学上册
文档属性
| 名称 | 1.2.3 绝对值课件 (共18张PPT)湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 160.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第一章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
1.知道绝对值的概念,用数轴体会绝对值的实际意义.
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
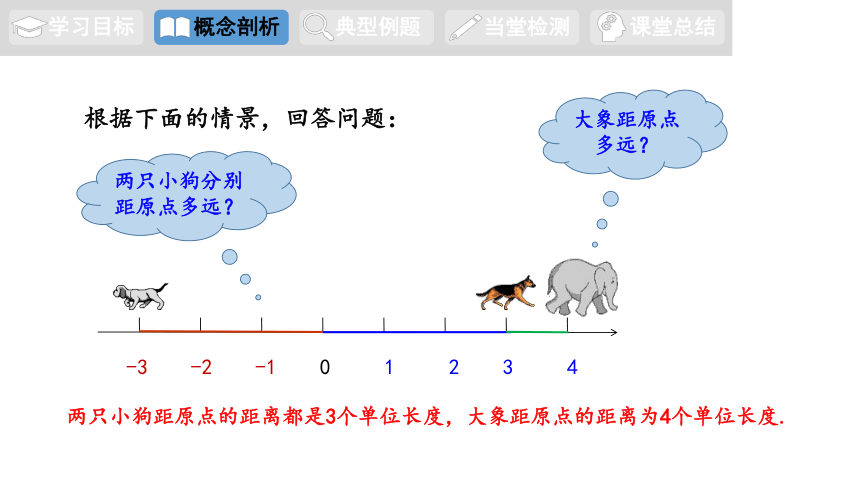
根据下面的情景,回答问题:
-3 -2 -1 0 1 2 3 4
大象距原点多远?
两只小狗分别距原点多远?
两只小狗距原点的距离都是3个单位长度,大象距原点的距离为4个单位长度.
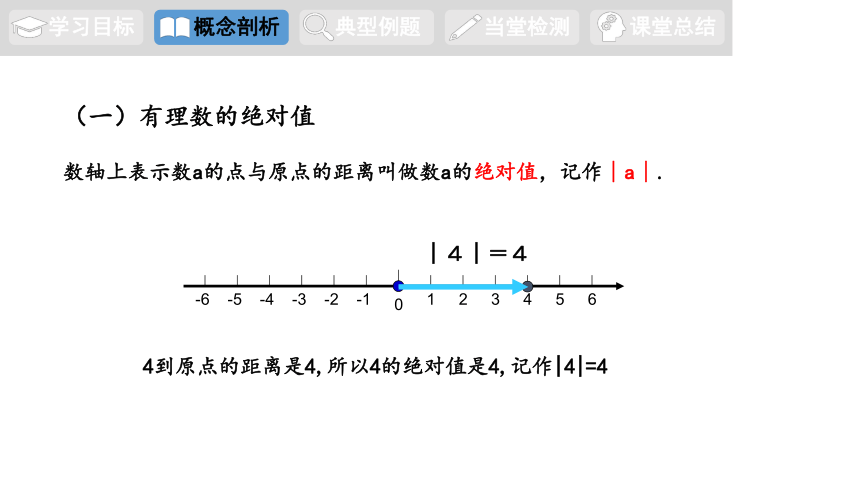
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│4│=4
(一)有理数的绝对值
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作∣a∣.
(一)有理数的绝对值
-5到原点的距离是5,所以-5的绝对值是5,记作∣-5∣=5
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
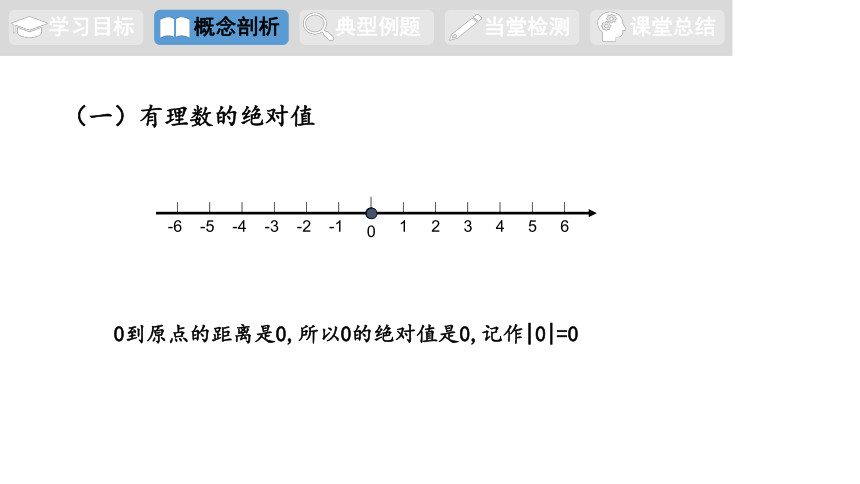
(一)有理数的绝对值
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
一个正数的绝对值是它本身;
(二)绝对值的性质
0的绝对值是0.
一个负数的绝对值是它的相反数;
(二)绝对值的性质
(1)当a是正数时,∣a∣= ;
(2)当a是负数时,∣a∣= ;
(3)当a=0时,∣a∣= .
a
- a
0
如果用字母a表示一个数,
例1.求下列各数的绝对值.
解:
|-0.1|=0.1;
;
|+1|=1;
|4.5|=4.5;
当a是负数时,|a|=-a
当a是正数时,|a|=a
总结:
0的绝对值等于0.
一个负数的绝对值等于它的相反数.
一个正数的绝对值等于它本身.
1.求下列各数的绝对值:3,3.14, ,-2.8.
|3.14|=3.14;
|-2.8|=2.8
解:∣3∣=3
2.点A为数轴上表示-2,当点A沿数轴移动4个单位长度到点B时,点B所表示的实数为( )
A.2 B. -6
C.2或-6 D.不同于以上答案
解析:利用数轴,可以直观地看到问题的答案.
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
A
向右移动4个单位,B点为2.
向左移动4个单位,B点为-6.
C
3.如图,数轴上的点A所表示的是有理数a,则点A到原点的距离是 .
解析:由数组可以看出,点A到原点的距离为a,因为a小于0,由绝对值的意义可知,点A到原点的距离为-a.
a
0
A
-a
例2.在数轴上表示出下列各点,并分别指出他们的绝对值.
-4, ,-2,0,4,-0.5,7
4, ,2, 0,4,0.5, 7
解:它们在数轴上表示为:
它们的绝对值分别是:
-4 -2 -0.5 0 4 7
任意数的绝对值都大于或等于0.
总结:
互为相反数的两个数的绝对值相等.
若一个数的绝对值是正数,则这样的数有两个,它们互为相反数.
例3.已知|x|=2,|y|=3,且x解析:由绝对值的定义知x=±2,y=±3,再由x解:因为|x|=2,|y|=3,
所以x=±2,y=±3.
又因为x所以x=2,y=3或x=-2,y=3.
4.填空
(1) |2|=______,|-2|=______.
(2) 若|x|=4,则x=_____.
(3) 若|a|=0,则a=______.
(4) |-6|的相反数是______.
(5) +7.2的相反数的绝对值是______.
±4
2
-6
7.2
2
0
数轴上表示数a的点与原点的距离,记作|a|
性质
绝对值
概念
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
第一章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
1.知道绝对值的概念,用数轴体会绝对值的实际意义.
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
根据下面的情景,回答问题:
-3 -2 -1 0 1 2 3 4
大象距原点多远?
两只小狗分别距原点多远?
两只小狗距原点的距离都是3个单位长度,大象距原点的距离为4个单位长度.
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│4│=4
(一)有理数的绝对值
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作∣a∣.
(一)有理数的绝对值
-5到原点的距离是5,所以-5的绝对值是5,记作∣-5∣=5
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
(一)有理数的绝对值
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
一个正数的绝对值是它本身;
(二)绝对值的性质
0的绝对值是0.
一个负数的绝对值是它的相反数;
(二)绝对值的性质
(1)当a是正数时,∣a∣= ;
(2)当a是负数时,∣a∣= ;
(3)当a=0时,∣a∣= .
a
- a
0
如果用字母a表示一个数,
例1.求下列各数的绝对值.
解:
|-0.1|=0.1;
;
|+1|=1;
|4.5|=4.5;
当a是负数时,|a|=-a
当a是正数时,|a|=a
总结:
0的绝对值等于0.
一个负数的绝对值等于它的相反数.
一个正数的绝对值等于它本身.
1.求下列各数的绝对值:3,3.14, ,-2.8.
|3.14|=3.14;
|-2.8|=2.8
解:∣3∣=3
2.点A为数轴上表示-2,当点A沿数轴移动4个单位长度到点B时,点B所表示的实数为( )
A.2 B. -6
C.2或-6 D.不同于以上答案
解析:利用数轴,可以直观地看到问题的答案.
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
A
向右移动4个单位,B点为2.
向左移动4个单位,B点为-6.
C
3.如图,数轴上的点A所表示的是有理数a,则点A到原点的距离是 .
解析:由数组可以看出,点A到原点的距离为a,因为a小于0,由绝对值的意义可知,点A到原点的距离为-a.
a
0
A
-a
例2.在数轴上表示出下列各点,并分别指出他们的绝对值.
-4, ,-2,0,4,-0.5,7
4, ,2, 0,4,0.5, 7
解:它们在数轴上表示为:
它们的绝对值分别是:
-4 -2 -0.5 0 4 7
任意数的绝对值都大于或等于0.
总结:
互为相反数的两个数的绝对值相等.
若一个数的绝对值是正数,则这样的数有两个,它们互为相反数.
例3.已知|x|=2,|y|=3,且x
所以x=±2,y=±3.
又因为x
4.填空
(1) |2|=______,|-2|=______.
(2) 若|x|=4,则x=_____.
(3) 若|a|=0,则a=______.
(4) |-6|的相反数是______.
(5) +7.2的相反数的绝对值是______.
±4
2
-6
7.2
2
0
数轴上表示数a的点与原点的距离,记作|a|
性质
绝对值
概念
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
同课章节目录
