1.2.2 相反数课件(共17张PPT) 湘教版七年级数学上册
文档属性
| 名称 | 1.2.2 相反数课件(共17张PPT) 湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 19:45:56 | ||
图片预览






文档简介
(共17张PPT)
第一章 有理数
1.2 数轴、相反数与绝对值
1.2.2 相反数
1.明确相反数的定义,会求一个数的相反数
2.用数轴探究相反数的几何意义,知道数轴上的两个
相反数在原点两侧,且距离相等
高和矮相反,上和下相反,亮和暗相反;生活中有许许多多的相反的概念;那么我们的数字有没有它相反的一面呢?一个数字的相反的一面与它又有什么关系呢?
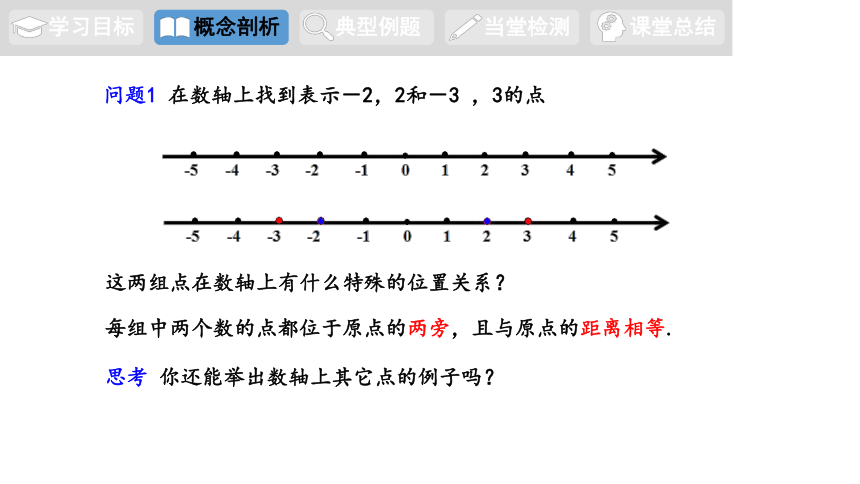
问题1 在数轴上找到表示-2,2和-3 ,3的点
这两组点在数轴上有什么特殊的位置关系?
每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考 你还能举出数轴上其它点的例子吗?
问题2 观察数轴,说出在数轴上与原点的距离是 2的点有几个?
这些点各表示哪些数?设a是一个正数,数轴上与原点的距离
等于a的点有几个?这些点表示的数有什么关系?
数轴上与原点的距离是2的点有两个,表示为-2和2;
如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a.
定义 像-2和2,-3和3这样,只有符号不同的两个数叫做互为相反数.
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等.
一般地,数a的相反数是-a,a可以是正数、负数或0.
规定:0的相反数是0,即- 0=0.
例1 说出下列各式的含义,并进行化简:
(1)-(+5)表示什么?化简的结果是多少?
(2)-(-5)表示什么?化简的结果是多少?
(3)-0表示什么呢?化简的结果是多少?
解:上面的式子分别表示+5、-5与0的相反数;
化简的结果分别是:
(1)-(+5)=-5;
(2)-(-5)=+5;
(3)-0=0.
例2 写出下列各数的相反数
5 ,- 7 ,-3.4 ,0 ,+ 6.82
解:5的相反数是- 5,
+6.82的相反数是-6.82.
-7的相反数是+ 7,
-3.4的相反数是+3.4,
0的相反数是0,
总结:正数的相反数在它前面添一个“ – ”号;负数的相
反数则把前面的“ – ”号改成“ + ”;0 的相反数是 0.
1.下列说法错误的是( )
A.-2的相反数是2 B.任何数的相反数都是负数
C.0的相反数是0 D.互为相反数的两个数相加等于0
B
2.-2019的相反数是( )
A.2019 B.-2019 C.-9102 D.
A
例3 (1)点A在数轴上的位置如图所示,则点A与A的相反数距离是 .
4
分析:由数轴可知,A点表示的数是2,它在原点的右侧,它到原点的距离是2;
它的相反数是-2,在原点的左侧,到原点的距离是2;
故点A与A的相反数的距离是4.
(2)已知-1、3在数轴上的位置如图所示.在数轴上作出它们的相反数;说说每组相反数在数轴上的位置关系特点.
0
3
-1
1
-3
解:-1、3的相反数分别为1、-3,数轴上表示如图;
它们的相反数在原点的另一侧,且与原点的距离相等.
总结:在数轴上表示互为相反数的两个数的点,分别位于原
点的两旁,且与原点的距离相等.
3.一个数在数轴上所对应的点向左移6个单位后,得到它的相反数的点,则这个数是( )
A.3 B.-3 C.6 D.-6
A
4.-(-a)的相反数是 .
-a
5.一个数a的相反数是非负数,那么这个数a与0的大小关系是a 0.
≤
只有符号不同的两个数,我们说其中一个是另一个的相反数.
数轴上的意义
相反数
概念
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等.
第一章 有理数
1.2 数轴、相反数与绝对值
1.2.2 相反数
1.明确相反数的定义,会求一个数的相反数
2.用数轴探究相反数的几何意义,知道数轴上的两个
相反数在原点两侧,且距离相等
高和矮相反,上和下相反,亮和暗相反;生活中有许许多多的相反的概念;那么我们的数字有没有它相反的一面呢?一个数字的相反的一面与它又有什么关系呢?
问题1 在数轴上找到表示-2,2和-3 ,3的点
这两组点在数轴上有什么特殊的位置关系?
每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考 你还能举出数轴上其它点的例子吗?
问题2 观察数轴,说出在数轴上与原点的距离是 2的点有几个?
这些点各表示哪些数?设a是一个正数,数轴上与原点的距离
等于a的点有几个?这些点表示的数有什么关系?
数轴上与原点的距离是2的点有两个,表示为-2和2;
如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a.
定义 像-2和2,-3和3这样,只有符号不同的两个数叫做互为相反数.
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等.
一般地,数a的相反数是-a,a可以是正数、负数或0.
规定:0的相反数是0,即- 0=0.
例1 说出下列各式的含义,并进行化简:
(1)-(+5)表示什么?化简的结果是多少?
(2)-(-5)表示什么?化简的结果是多少?
(3)-0表示什么呢?化简的结果是多少?
解:上面的式子分别表示+5、-5与0的相反数;
化简的结果分别是:
(1)-(+5)=-5;
(2)-(-5)=+5;
(3)-0=0.
例2 写出下列各数的相反数
5 ,- 7 ,-3.4 ,0 ,+ 6.82
解:5的相反数是- 5,
+6.82的相反数是-6.82.
-7的相反数是+ 7,
-3.4的相反数是+3.4,
0的相反数是0,
总结:正数的相反数在它前面添一个“ – ”号;负数的相
反数则把前面的“ – ”号改成“ + ”;0 的相反数是 0.
1.下列说法错误的是( )
A.-2的相反数是2 B.任何数的相反数都是负数
C.0的相反数是0 D.互为相反数的两个数相加等于0
B
2.-2019的相反数是( )
A.2019 B.-2019 C.-9102 D.
A
例3 (1)点A在数轴上的位置如图所示,则点A与A的相反数距离是 .
4
分析:由数轴可知,A点表示的数是2,它在原点的右侧,它到原点的距离是2;
它的相反数是-2,在原点的左侧,到原点的距离是2;
故点A与A的相反数的距离是4.
(2)已知-1、3在数轴上的位置如图所示.在数轴上作出它们的相反数;说说每组相反数在数轴上的位置关系特点.
0
3
-1
1
-3
解:-1、3的相反数分别为1、-3,数轴上表示如图;
它们的相反数在原点的另一侧,且与原点的距离相等.
总结:在数轴上表示互为相反数的两个数的点,分别位于原
点的两旁,且与原点的距离相等.
3.一个数在数轴上所对应的点向左移6个单位后,得到它的相反数的点,则这个数是( )
A.3 B.-3 C.6 D.-6
A
4.-(-a)的相反数是 .
-a
5.一个数a的相反数是非负数,那么这个数a与0的大小关系是a 0.
≤
只有符号不同的两个数,我们说其中一个是另一个的相反数.
数轴上的意义
相反数
概念
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等.
同课章节目录
