1.6.1 有理数的乘方 课件(共15张PPT) 湘教版数学七年级上册
文档属性
| 名称 | 1.6.1 有理数的乘方 课件(共15张PPT) 湘教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第一章 有理数
1.6.1 有理数的乘方
1.知道乘方表示的意义及乘方运算的相关概念
2.能熟练地进行有理数的乘方运算
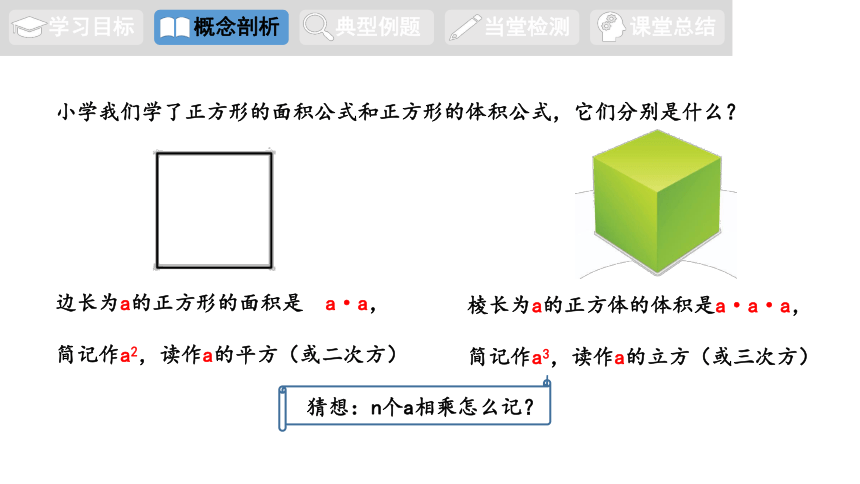
小学我们学了正方形的面积公式和正方形的体积公式,它们分别是什么?
猜想:n个a相乘怎么记?
边长为a的正方形的面积是 a·a,
简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,
简记作a3,读作a的立方(或三次方)
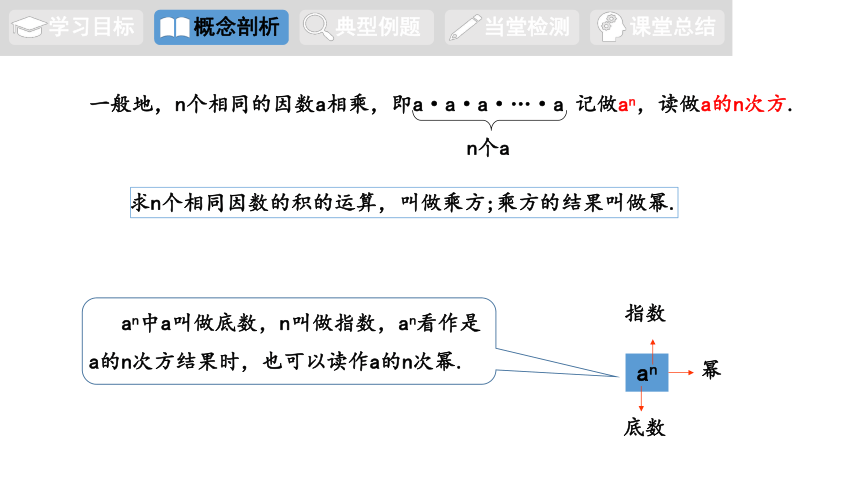
求n个相同因数的积的运算,叫做乘方;乘方的结果叫做幂.
an
底数
幂
指数
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方.
n个a
an中a叫做底数,n叫做指数,an看作是
a的n次方结果时,也可以读作a的n次幂.
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂.
一个数可以看作这个数本身的一次方,例如:5就是51,指数
是1通常省略不写.
想一想:至今我们所学的有理数的运算包括哪些?
有理数的加法、减法、乘法、除法、乘方
注意:我们目前所学过的运算通常分成三级;加与减是第一级运算,乘
与除是第二级运算,乘方是第三级运算.运算时顺序是先进行高级运算
再进行低级运算.
先算乘方,再算乘除
例如在22×3这个式子中,先算2的平方,再算平方与3的乘积.
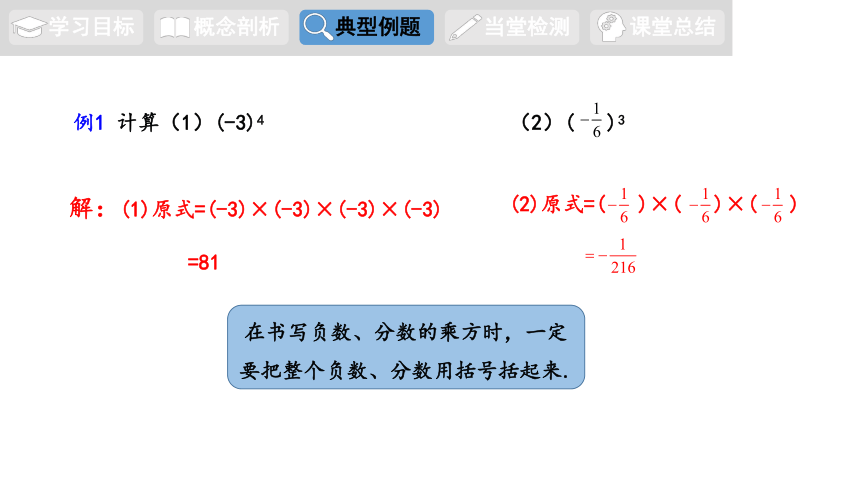
例1 计算(1)(-3)4 (2)( )3
解:(1)原式=(-3)×(-3)×(-3)×(-3)
=81
在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
(2)原式=( )×( )×( )
例2 计算(1)-34 (2)(-3)4 (3)-(-3)4
解:(1)原式=-(3×3×3×3)
=-81
(2)原式=(-3)×(-3)×(-3)×(-3)
=81
(3)原式=-[(-3)×(-3)×(-3)×(-3)]
=-(+81)
=-81
注意这些式子的运算顺序
例3 计算
(1)22, 23,24, 25 (2)(-2)2 ,(-2)3 ,(-2)4 ,(-2)5
解:(1)22=2×2=4
23=2×2×2=8
24=2×2×2×2=16
25=2×2×2×2×2=32
(2)(-2)2=(-2)×(-2)=4
(-2)3=(-2)×(-2)×(-2)=-8
(-2)4=(-2)×(-2)×(-2)×(-2)=16
(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32
观察上面各式的计算结果,你发现了什么规律?
归纳总结
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数.
0的任何次幂都是0.
1.填空
(1)在25中,底数是 ,指数是 ,读做 ,或 .
(2)一个数可以看作这个数本身的 次方.
2
2的5次方
5
2的5次幂
一
2.计算(1)(-0.1)3 (2)( )4
(2)原式
(1)原式 =(-0.1)×(-0.1)×(-0.1)
解:
= 0.01 × (-0.1)
= -0.001
3.判断下列各式结果的符号
(1) -29 (2) (-3)32 (3) 625 (4) -(-8)11 (5) (-7)69
解:(1)的结果是负号;
(2)的结果是正号;
(3)的结果是正号;
(4)的结果是正号;
(5)的结果是负号.
4.设n为正整数,求(-1)2n和(-1)2n+1的值.
分析:先判断指数的奇偶性,再根据“负数的奇次幂是负数,负数的偶次幂是正数”求出结果.
解:因为n为正整数,所以2n为偶数,2n+1为奇数,
所以(-1)2n的结果为正,(-1)2n+1的结果为负;
又因为-1的正整数次方结果只有-1和1;
所以(-1)2n的结果为1,(-1)2n+1的结果为-1.
1.乘方的概念:
n个相同的因数a相乘,即a·a·a·…·a 记做an,
读做a的n次方.
n个a
2.乘方符号的确定:
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数,0的任何次幂都是0.
3.有理数乘方的运算顺序:先算乘方,再算乘除.
第一章 有理数
1.6.1 有理数的乘方
1.知道乘方表示的意义及乘方运算的相关概念
2.能熟练地进行有理数的乘方运算
小学我们学了正方形的面积公式和正方形的体积公式,它们分别是什么?
猜想:n个a相乘怎么记?
边长为a的正方形的面积是 a·a,
简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,
简记作a3,读作a的立方(或三次方)
求n个相同因数的积的运算,叫做乘方;乘方的结果叫做幂.
an
底数
幂
指数
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方.
n个a
an中a叫做底数,n叫做指数,an看作是
a的n次方结果时,也可以读作a的n次幂.
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂.
一个数可以看作这个数本身的一次方,例如:5就是51,指数
是1通常省略不写.
想一想:至今我们所学的有理数的运算包括哪些?
有理数的加法、减法、乘法、除法、乘方
注意:我们目前所学过的运算通常分成三级;加与减是第一级运算,乘
与除是第二级运算,乘方是第三级运算.运算时顺序是先进行高级运算
再进行低级运算.
先算乘方,再算乘除
例如在22×3这个式子中,先算2的平方,再算平方与3的乘积.
例1 计算(1)(-3)4 (2)( )3
解:(1)原式=(-3)×(-3)×(-3)×(-3)
=81
在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
(2)原式=( )×( )×( )
例2 计算(1)-34 (2)(-3)4 (3)-(-3)4
解:(1)原式=-(3×3×3×3)
=-81
(2)原式=(-3)×(-3)×(-3)×(-3)
=81
(3)原式=-[(-3)×(-3)×(-3)×(-3)]
=-(+81)
=-81
注意这些式子的运算顺序
例3 计算
(1)22, 23,24, 25 (2)(-2)2 ,(-2)3 ,(-2)4 ,(-2)5
解:(1)22=2×2=4
23=2×2×2=8
24=2×2×2×2=16
25=2×2×2×2×2=32
(2)(-2)2=(-2)×(-2)=4
(-2)3=(-2)×(-2)×(-2)=-8
(-2)4=(-2)×(-2)×(-2)×(-2)=16
(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32
观察上面各式的计算结果,你发现了什么规律?
归纳总结
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数.
0的任何次幂都是0.
1.填空
(1)在25中,底数是 ,指数是 ,读做 ,或 .
(2)一个数可以看作这个数本身的 次方.
2
2的5次方
5
2的5次幂
一
2.计算(1)(-0.1)3 (2)( )4
(2)原式
(1)原式 =(-0.1)×(-0.1)×(-0.1)
解:
= 0.01 × (-0.1)
= -0.001
3.判断下列各式结果的符号
(1) -29 (2) (-3)32 (3) 625 (4) -(-8)11 (5) (-7)69
解:(1)的结果是负号;
(2)的结果是正号;
(3)的结果是正号;
(4)的结果是正号;
(5)的结果是负号.
4.设n为正整数,求(-1)2n和(-1)2n+1的值.
分析:先判断指数的奇偶性,再根据“负数的奇次幂是负数,负数的偶次幂是正数”求出结果.
解:因为n为正整数,所以2n为偶数,2n+1为奇数,
所以(-1)2n的结果为正,(-1)2n+1的结果为负;
又因为-1的正整数次方结果只有-1和1;
所以(-1)2n的结果为1,(-1)2n+1的结果为-1.
1.乘方的概念:
n个相同的因数a相乘,即a·a·a·…·a 记做an,
读做a的n次方.
n个a
2.乘方符号的确定:
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数,0的任何次幂都是0.
3.有理数乘方的运算顺序:先算乘方,再算乘除.
同课章节目录
