1.5.1 有理数的乘法 第1课时课件 (共18张PPT)湘教版七年级数学上册
文档属性
| 名称 | 1.5.1 有理数的乘法 第1课时课件 (共18张PPT)湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 611.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 20:02:54 | ||
图片预览





文档简介
(共18张PPT)
第1课时
第一章 有理数
1.5.1 有理数的乘法
1.了解有理数乘法的实际意义,理解有理数的乘法法则
2.掌握有理数乘法的运算步骤,能熟练进行有理数乘法运算
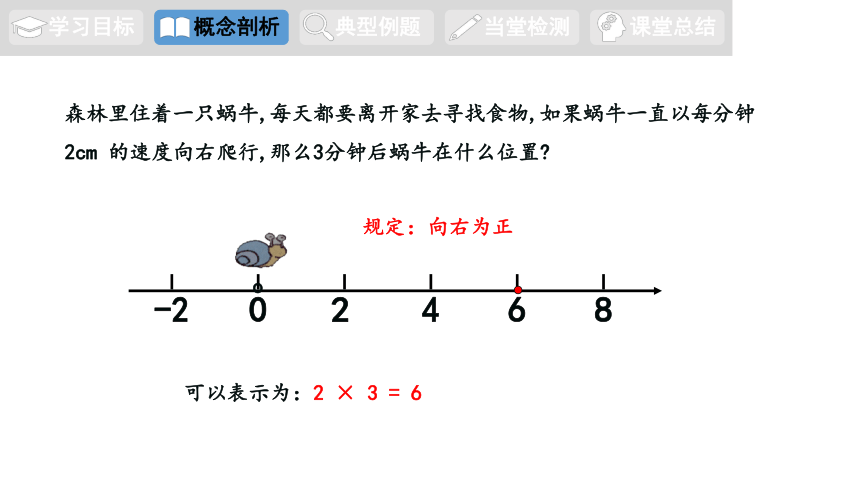
森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置
-2
0
2
4
6
8
o
可以表示为:2 × 3 = 6
规定:向右为正
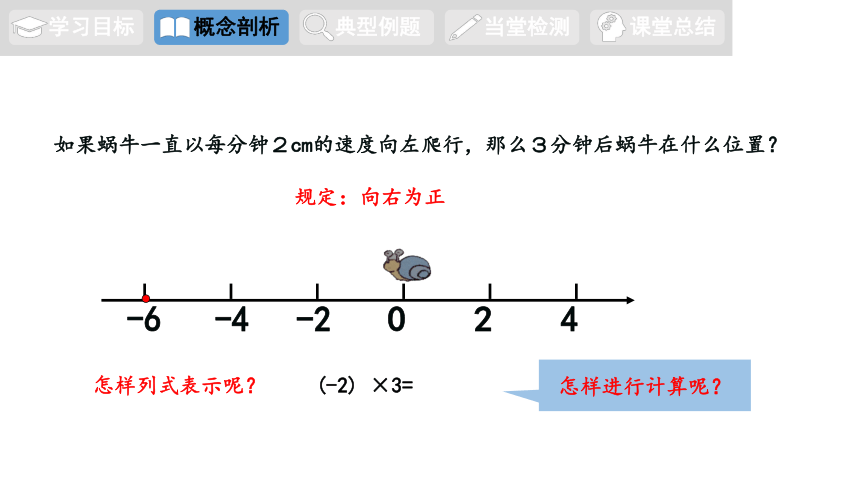
如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?
-6
-4
-2
0
2
4
怎样列式表示呢?
规定:向右为正
(-2) ×3=
怎样进行计算呢?
如图,我们把向东走的路程记为正数.如果小丽从O点出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?
思考
(-5)×3=-(5×3)
小丽从O点向西行走了(5×3)km.
列式为:
我们已经知道(-5)×3=-(5×3),那么3×(-5),(-5)×(-3)又应该怎么计算呢?
非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,也要求它满足分配律,以便把乘法与加法联系起来.
即:3×(-5)+3×5=3×[(-5)+5]=3×0=0
所以可知3×(-5)与3×5互为相反数
即:3×(-5)=-(3×5)
异号两数相乘得负数,并把绝对值相乘.
(-) ×(+) (-)
(+) ×(-) (-)
任何数与0相乘,都得0
归纳总结
类似地,我们有
(-5) ×(-3)+(-5) ×3
=(-5) ×[(-3)+3]
=(-5) ×0
=0
所以(-5) ×(-3)+(-5) ×3互为相反数
即:(-5) ×(-3)=15=5×3
因为(-5) ×3=-15,-15的相反数是15
所以(-5) ×(-3)=15
同号两数相乘得正数,并把绝对值相乘.
(+) ×(+) (+)
(-) ×(-) (+)
归纳总结
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
例1 计算
(1)3.5×(-2) (2)() ×
解:(1)3.5×(-2)
注意:第一个负因数可以不加括号,但后面的负因数必须加括号.
(2)
=-(3.5×2)
=-7
(3)(-3) ×()
有理数相乘,先确定积的符号,再求绝对值的积.
(3)(-3) ×(-) (4)(-0.57) ×0
(4)(-0.57) ×0=0
=3×
(1)6×(-9);
(2)4×5;
(3)(-7)×(-9);
(4)(-12)×3.
确定下列两数积的符号,并计算
负
负
正
正
6×(-9)=-54
4×5=20
(-7)×(-9)=63
(-12)×3=-36
练一练
做一做
(1)3×(-1) (2)(-5) ×(-1) (3)1×(-1) (4)0×(-1)
(5)(-6) ×1 (6)2×1 (7)0×1
你能发现什么?
注意
(1)一个数同+1相乘,得原数
(2)一个数同-1相乘,得原数的相反数.
1.如图所示,数轴上A,B两点所表示的两数的 ( )
A.和为正数 B.和为负数 C.积为正数 D.积为负数
2.一个有理数和它的相反数的积一定是( )
A.正数 B.负数 C.非正数 D.非负数
D
C
3.若|a|=5,b=-2,且ab>0,则a+b= .
-7
>
4.若a<b<0,则ab 0,a﹣b 0.(用“<或>”填空)
<
5.计算
(-6) ×8 (2) (-0.36) ×
(3) (4)
解:(1)(-6) ×8=-48
(2) (-0.36) ×=0.08
(3) =
(4) =0
带分数在进行乘法运算时,必须化为假分数.
有
理
数
的
乘
法
法则
步骤
两个有理数相乘,先确定积的符号,再确定积的绝对值.
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
第1课时
第一章 有理数
1.5.1 有理数的乘法
1.了解有理数乘法的实际意义,理解有理数的乘法法则
2.掌握有理数乘法的运算步骤,能熟练进行有理数乘法运算
森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置
-2
0
2
4
6
8
o
可以表示为:2 × 3 = 6
规定:向右为正
如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?
-6
-4
-2
0
2
4
怎样列式表示呢?
规定:向右为正
(-2) ×3=
怎样进行计算呢?
如图,我们把向东走的路程记为正数.如果小丽从O点出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?
思考
(-5)×3=-(5×3)
小丽从O点向西行走了(5×3)km.
列式为:
我们已经知道(-5)×3=-(5×3),那么3×(-5),(-5)×(-3)又应该怎么计算呢?
非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,也要求它满足分配律,以便把乘法与加法联系起来.
即:3×(-5)+3×5=3×[(-5)+5]=3×0=0
所以可知3×(-5)与3×5互为相反数
即:3×(-5)=-(3×5)
异号两数相乘得负数,并把绝对值相乘.
(-) ×(+) (-)
(+) ×(-) (-)
任何数与0相乘,都得0
归纳总结
类似地,我们有
(-5) ×(-3)+(-5) ×3
=(-5) ×[(-3)+3]
=(-5) ×0
=0
所以(-5) ×(-3)+(-5) ×3互为相反数
即:(-5) ×(-3)=15=5×3
因为(-5) ×3=-15,-15的相反数是15
所以(-5) ×(-3)=15
同号两数相乘得正数,并把绝对值相乘.
(+) ×(+) (+)
(-) ×(-) (+)
归纳总结
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
例1 计算
(1)3.5×(-2) (2)() ×
解:(1)3.5×(-2)
注意:第一个负因数可以不加括号,但后面的负因数必须加括号.
(2)
=-(3.5×2)
=-7
(3)(-3) ×()
有理数相乘,先确定积的符号,再求绝对值的积.
(3)(-3) ×(-) (4)(-0.57) ×0
(4)(-0.57) ×0=0
=3×
(1)6×(-9);
(2)4×5;
(3)(-7)×(-9);
(4)(-12)×3.
确定下列两数积的符号,并计算
负
负
正
正
6×(-9)=-54
4×5=20
(-7)×(-9)=63
(-12)×3=-36
练一练
做一做
(1)3×(-1) (2)(-5) ×(-1) (3)1×(-1) (4)0×(-1)
(5)(-6) ×1 (6)2×1 (7)0×1
你能发现什么?
注意
(1)一个数同+1相乘,得原数
(2)一个数同-1相乘,得原数的相反数.
1.如图所示,数轴上A,B两点所表示的两数的 ( )
A.和为正数 B.和为负数 C.积为正数 D.积为负数
2.一个有理数和它的相反数的积一定是( )
A.正数 B.负数 C.非正数 D.非负数
D
C
3.若|a|=5,b=-2,且ab>0,则a+b= .
-7
>
4.若a<b<0,则ab 0,a﹣b 0.(用“<或>”填空)
<
5.计算
(-6) ×8 (2) (-0.36) ×
(3) (4)
解:(1)(-6) ×8=-48
(2) (-0.36) ×=0.08
(3) =
(4) =0
带分数在进行乘法运算时,必须化为假分数.
有
理
数
的
乘
法
法则
步骤
两个有理数相乘,先确定积的符号,再确定积的绝对值.
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
同课章节目录
