数学人教A版(2019)必修第一册5.1.2弧度制(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 60.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 20:41:15 | ||
图片预览




文档简介
(共17张PPT)
5.1.2 弧度制
人教A版(2019)必修1
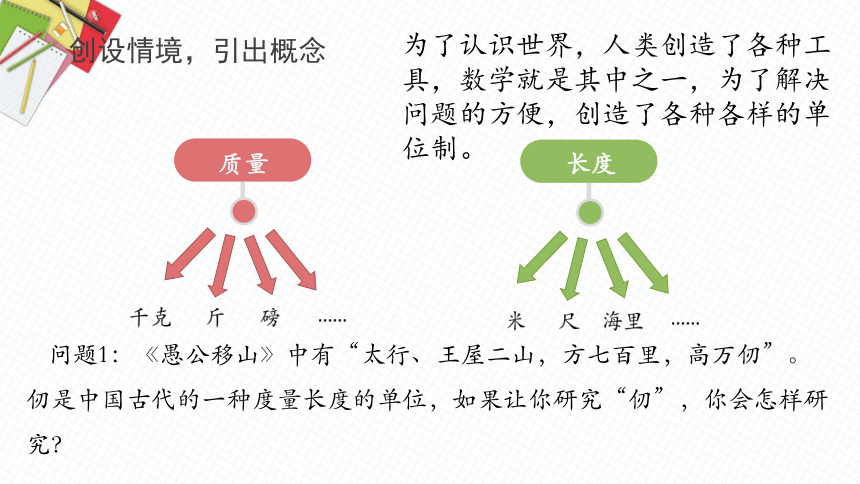
创设情境,引出概念
质量
长度
千克
磅
斤
......
米
海里
尺
......
问题1:《愚公移山》中有“太行、王屋二山,方七百里,高万仞”。仞是中国古代的一种度量长度的单位,如果让你研究“仞”,你会怎样研究?
为了认识世界,人类创造了各种工具,数学就是其中之一,为了解决问题的方便,创造了各种各样的单位制。
创设情境,引出概念
角度制
约在公元前2000年,古巴比伦人创设性地将圆周划分为360度,每度分为60分,每分再划分为60秒
2.这种用度作为单位来度量角的单位制叫做角度制(degree measure)
公元6世纪,印度的数学家阿耶波多在制作正弦函数表的时候,他发现一个问题不好解释。如:sin30°=
1.规定:周角的为一度的角
创设情境,引出概念
角度制
约在公元前2000年,古巴比伦人创设性地将圆周划分为360度,每度分为60分,每分再划分为60秒
1.规定:周角的 叫做1度的角。
2.这种用度作为单位来度量角的单位制叫做角度制(degree measure)
角度能否有其他的度量方法呢?
合作探究,构建概念
某地为宣扬社会主义核心价值观,需要生产一个和图中一样的扇形广告宣传牌,技术人员需要计算以下扇形的面积,用来测算原材料的量。若他手里只有一卷钢卷尺和细线若干,能用现有的工具测出扇形的大致面积吗?
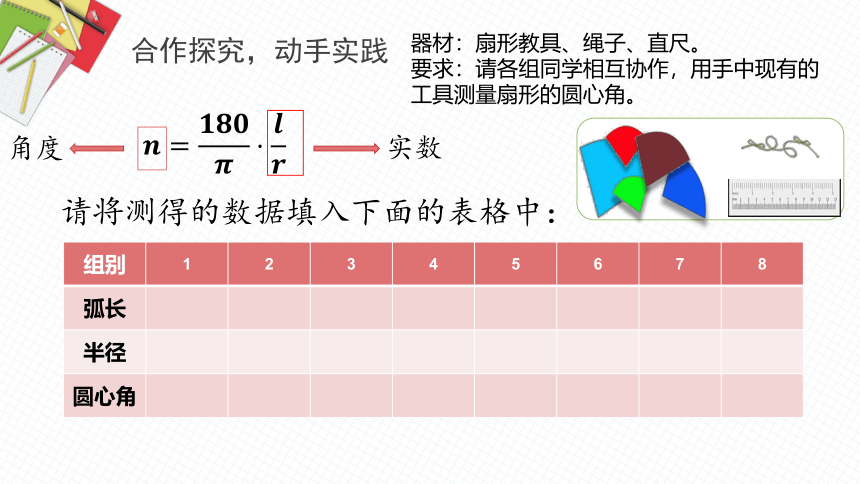
合作探究,动手实践
请将测得的数据填入下面的表格中:
组别 1 2 3 4 5 6 7 8
弧长
半径
圆心角
实数
角度
器材:扇形教具、绳子、直尺。
要求:请各组同学相互协作,用手中现有的工具测量扇形的圆心角。
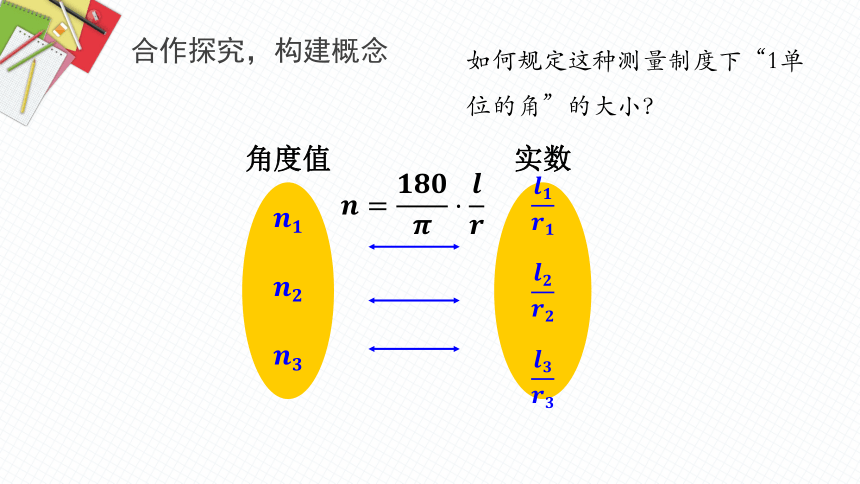
合作探究,构建概念
角度值
实数
如何规定这种测量制度下“1单位的角”的大小?
合作探究,构建概念
规定:把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,弧度单位用符号rad表示,读作弧度. 用弧度作为角的单位来度量角的单位制称为弧度制.
1rad
-1rad
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
思考:圆的半径为r , 弧长分别为2r,3r,2πr的弧所对的的圆心角的弧度数是多少?
360°=2π rad
合作探究,构建概念
早在18世纪,伟大的瑞士数学家欧拉(1707-1783)在他的名著《无穷小分析引论》中倡导用弧度制,即以半径为单位来量弧长,统一了角和长度的单位。
1873年,詹姆斯·汤姆森教授在其编著的考试问题集中创造性地使用了“弧度”一 词。他将 “半径 ”(radius)的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,被人们广泛接受和引用。
弧度制的发展
分析应用,理解概念
例1.按照要求完成下列角的互化.(精确到0.001)
(1)把67°30′化成弧度 (2)把3.14rad化成角度.
角度制、弧度制都是角的度量制,它们之间如何换算呢?
分析应用,理解概念
常见特殊角的角度与弧度对应表:
实数集R
正角
零角
负角
正实数
零
负实数
角的集合
统一了三角函数自变量和函数值的单位
三角函数
实数(弧度制)
自变量
因变量
实数
情境再现,应用概念
请大家用弧度制证明下列关于扇形的公式
弧度制 角度制
弧长公式
扇形面积公式
简化公式
思考:由此你认为引入弧度制有何优势?
情景再现
某地为宣扬社会主义核心价值观,需要生产一个和图中一样的扇形广告宣传牌,技术人员需要计算以下扇形的面积,用来测算原材料的量。若他手里只有一卷钢卷尺和细线若干,能用现有的工具测出扇形的大致面积吗?
小结反思,感知升华
对照以下研究路径,说说你是如何研究弧度制的?
01
背景
定义
换算
应用
度量需要
单位1
角度弧度互化
简化公式
合理性
小结反思,感知升华
背景
定义
换算
应用
度量需要
单位1
角度弧度互化
简化公式
合理性
类比推理
转化化归
数形结合
发现问题
提出问题
解决问题
用数学的眼光观察世界
用数学的思维思考世界
用数学的语言表达世界
必做题
选做题
布置作业,巩固实践
① 课本P175练习题第6题
② 完成平板推送的素养达标小练
① 查阅资料了解弧度制的发展史.
② 查阅资料了解密位制,并结合角度制、弧度制、密位制的定义和应用,撰写小论文谈谈你对单位制的理解.
谢谢
5.1.2 弧度制
人教A版(2019)必修1
创设情境,引出概念
质量
长度
千克
磅
斤
......
米
海里
尺
......
问题1:《愚公移山》中有“太行、王屋二山,方七百里,高万仞”。仞是中国古代的一种度量长度的单位,如果让你研究“仞”,你会怎样研究?
为了认识世界,人类创造了各种工具,数学就是其中之一,为了解决问题的方便,创造了各种各样的单位制。
创设情境,引出概念
角度制
约在公元前2000年,古巴比伦人创设性地将圆周划分为360度,每度分为60分,每分再划分为60秒
2.这种用度作为单位来度量角的单位制叫做角度制(degree measure)
公元6世纪,印度的数学家阿耶波多在制作正弦函数表的时候,他发现一个问题不好解释。如:sin30°=
1.规定:周角的为一度的角
创设情境,引出概念
角度制
约在公元前2000年,古巴比伦人创设性地将圆周划分为360度,每度分为60分,每分再划分为60秒
1.规定:周角的 叫做1度的角。
2.这种用度作为单位来度量角的单位制叫做角度制(degree measure)
角度能否有其他的度量方法呢?
合作探究,构建概念
某地为宣扬社会主义核心价值观,需要生产一个和图中一样的扇形广告宣传牌,技术人员需要计算以下扇形的面积,用来测算原材料的量。若他手里只有一卷钢卷尺和细线若干,能用现有的工具测出扇形的大致面积吗?
合作探究,动手实践
请将测得的数据填入下面的表格中:
组别 1 2 3 4 5 6 7 8
弧长
半径
圆心角
实数
角度
器材:扇形教具、绳子、直尺。
要求:请各组同学相互协作,用手中现有的工具测量扇形的圆心角。
合作探究,构建概念
角度值
实数
如何规定这种测量制度下“1单位的角”的大小?
合作探究,构建概念
规定:把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,弧度单位用符号rad表示,读作弧度. 用弧度作为角的单位来度量角的单位制称为弧度制.
1rad
-1rad
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
思考:圆的半径为r , 弧长分别为2r,3r,2πr的弧所对的的圆心角的弧度数是多少?
360°=2π rad
合作探究,构建概念
早在18世纪,伟大的瑞士数学家欧拉(1707-1783)在他的名著《无穷小分析引论》中倡导用弧度制,即以半径为单位来量弧长,统一了角和长度的单位。
1873年,詹姆斯·汤姆森教授在其编著的考试问题集中创造性地使用了“弧度”一 词。他将 “半径 ”(radius)的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,被人们广泛接受和引用。
弧度制的发展
分析应用,理解概念
例1.按照要求完成下列角的互化.(精确到0.001)
(1)把67°30′化成弧度 (2)把3.14rad化成角度.
角度制、弧度制都是角的度量制,它们之间如何换算呢?
分析应用,理解概念
常见特殊角的角度与弧度对应表:
实数集R
正角
零角
负角
正实数
零
负实数
角的集合
统一了三角函数自变量和函数值的单位
三角函数
实数(弧度制)
自变量
因变量
实数
情境再现,应用概念
请大家用弧度制证明下列关于扇形的公式
弧度制 角度制
弧长公式
扇形面积公式
简化公式
思考:由此你认为引入弧度制有何优势?
情景再现
某地为宣扬社会主义核心价值观,需要生产一个和图中一样的扇形广告宣传牌,技术人员需要计算以下扇形的面积,用来测算原材料的量。若他手里只有一卷钢卷尺和细线若干,能用现有的工具测出扇形的大致面积吗?
小结反思,感知升华
对照以下研究路径,说说你是如何研究弧度制的?
01
背景
定义
换算
应用
度量需要
单位1
角度弧度互化
简化公式
合理性
小结反思,感知升华
背景
定义
换算
应用
度量需要
单位1
角度弧度互化
简化公式
合理性
类比推理
转化化归
数形结合
发现问题
提出问题
解决问题
用数学的眼光观察世界
用数学的思维思考世界
用数学的语言表达世界
必做题
选做题
布置作业,巩固实践
① 课本P175练习题第6题
② 完成平板推送的素养达标小练
① 查阅资料了解弧度制的发展史.
② 查阅资料了解密位制,并结合角度制、弧度制、密位制的定义和应用,撰写小论文谈谈你对单位制的理解.
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
