第25章 解直角三角形教案(福建省漳州市长泰县)
文档属性
| 名称 | 第25章 解直角三角形教案(福建省漳州市长泰县) |
|
|
| 格式 | rar | ||
| 文件大小 | 137.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-06 00:00:00 | ||
图片预览





文档简介
王鹏举 25章解直角三角形教案 第22页
第1课时 测量
教学目标:利用前面学习的相似三角形的有关知识,探索测量距离的几种方法,初步接触直角三角形的边角关系。
教学重点:探索测量距离的几种方法。
教学难点:选择适当的方法测量物体的高度或长度。
教学过程:
一。复习引入:
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许想知道操场旗杆有多高?我们知道可以利用相似三角形的对应边,首先请同学量出太阳下自己的影子长度,旗杆的影子长度,再根据自己的身高,计算出旗杆的高度。如果在阴天,你一个人能测量出旗杆的高度吗?
二。新课探究:
例1. 书.P.98试一试.
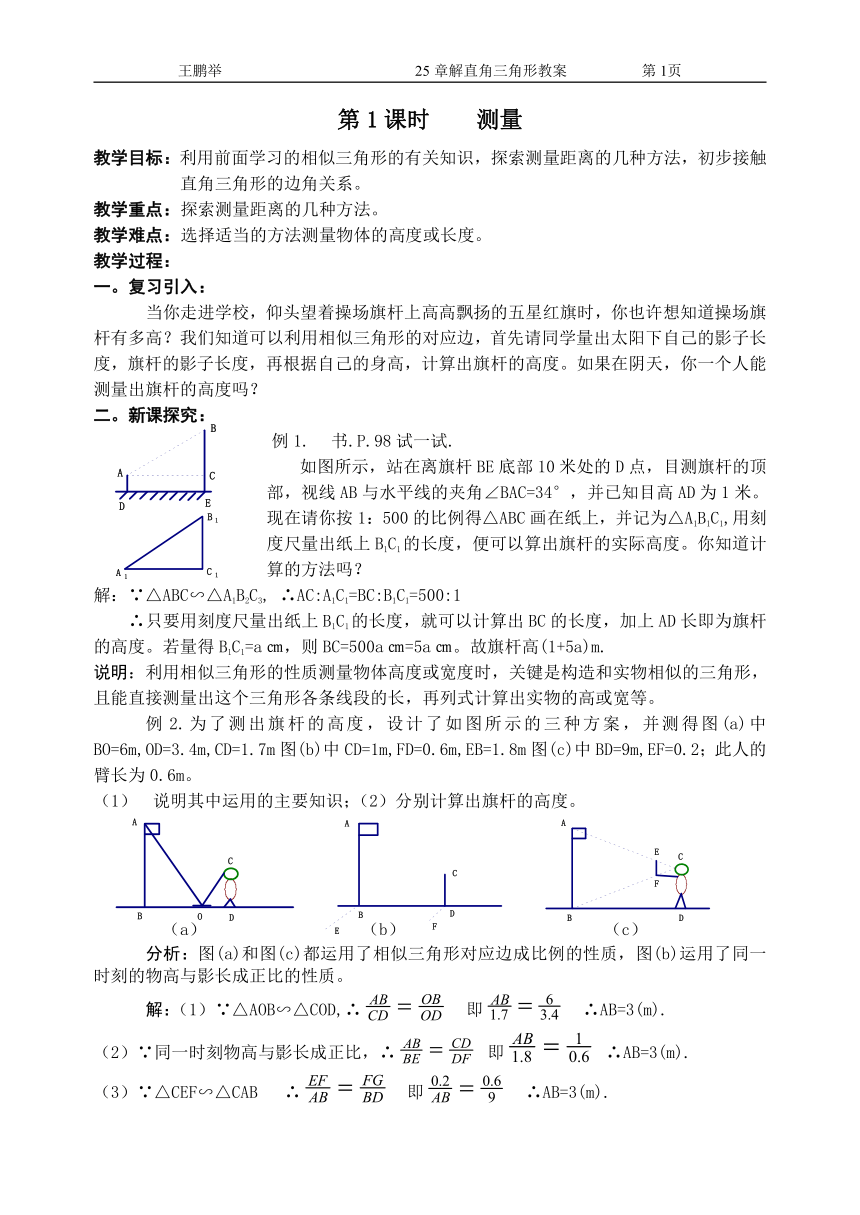
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1米。现在请你按1:500的比例得△ABC画在纸上,并记为△A1B1C1,用刻度尺量出纸上B1C1的长度,便可以算出旗杆的实际高度。你知道计算的方法吗?
解:∵△ABC∽△A1B2C3, ∴AC:A1C1=BC:B1C1=500:1
∴只要用刻度尺量出纸上B1C1的长度,就可以计算出BC的长度,加上AD长即为旗杆的高度。若量得B1C1=a㎝,则BC=500a㎝=5a㎝。故旗杆高(1+5a)m.
说明:利用相似三角形的性质测量物体高度或宽度时,关键是构造和实物相似的三角形,且能直接测量出这个三角形各条线段的长,再列式计算出实物的高或宽等。
例2.为了测出旗杆的高度,设计了如图所示的三种方案,并测得图(a)中BO=6m,OD=3.4m,CD=1.7m图(b)中CD=1m,FD=0.6m,EB=1.8m图(c)中BD=9m,EF=0.2;此人的臂长为0.6m。
(1) 说明其中运用的主要知识;(2)分别计算出旗杆的高度。
(a) (b) (c)
分析:图(a)和图(c)都运用了相似三角形对应边成比例的性质,图(b)运用了同一时刻的物高与影长成正比的性质。
解:(1)∵△AOB∽△COD,∴ 即 ∴AB=3(m).
(2)∵同一时刻物高与影长成正比,∴ 即 ∴AB=3(m).
(3)∵△CEF∽△CAB ∴ 即 ∴AB=3(m).
方法技巧:测量物体的高度可利用自己的身高、臂长等长度结合相似形的性质求出物高,也可以运用同一时刻的物高与影长成正比的性质测量物体的高度。
三、引申提高:
例3。设计一种方案,测量学校科技楼的高度。请写出测量的过程,并简要说明这样做的理由。
分析:测量大楼的高度的方法很多,现采用一种方法,利用人的身高和标杆,依据相似三角形三角对应成比例和平行线的性质,可测出大楼的高度。
解答:测量过程如下:
1、在地面上立一个标杆,使人眼、杆顶、楼顶在一条直线上。
2、测出CF、CH的距离。
大楼 3、算出KE的长度。
4、用标杆长度减去人的身高,即DE的长度。
标杆 5、由DE∥AB得△KDE∽△KAB。又因为相似三角形三边对应成比例,∴。
6、再将刚才测量的数值代入比例式中,计算出AB的长度。
7、用AB加上人的身高即得出大楼的高度。
探究点拔:1.选择测量的方法应是切实可行的。如本题中人眼、杆顶、楼顶在一条直线上(人是站立的)。
2.大楼的高度=AB+人高。
3.测量的过程要清楚,力求每步都有根有据,达到学以至用。
四.巩固练习:
1.如图1,要测量A、B两点间距离,在O点设桩,取OA中点C,OB中点D,测得CD=31.4m 求AB长。 (AB=62.8m)
(1) (2)
2. 如图2, 为了测量河的宽度,可以先在河对岸找到一个具有明显标志的点A,再在所在的一边找到两点B、C,使△ABC构成Rt△。如果测得BC=50米,∠ABC=73°,试设计一种方法求河的宽度AC。 (在地面上另作 Rt△A’B’C’,使B’C’=5米,∠C’=Rt∠,∠B’=73°, 测得 A’C’=16.35米,得 AC=16.35米 ).
五.课时小结:
选择适当的方法测量物体的高度或长度等是新时期素质教育的要求,运用所学相似三角形知识设计测量方案时一定要考虑可行性,力求操作简便,计算简洁,同时注意分析环境、天气等要素。
六.课堂作业:
P.73 习题25.1 1、2、3
第2课时 锐角三角函数(1)
教学目标:1.直角三角形可简记为Rt△ABC
2.理解Rt△中锐角的正弦、余弦、正切、余切的概念。
教学重点:四种锐角三角函数的定义。
教学难点:理解锐角三角函数的定义。
教学过程:
一.复习提问:
1. 什么叫Rt△?它的三边有何关系?
2.Rt△中角、边之间的关系是:①∠A+∠B=90°②
二.新课探究:
1.Rt△ABC中,某个角的对边、邻边的介绍。
2.如图,由Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
得
可见,在Rt△ABC中,对于锐角A的每一
个确定的值,其对边与邻边的比值是惟一确定的。
同样,其对边与斜边,邻边与斜边,邻边与对边的比值也是惟一确定的。
3.四种锐角三角函数。
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
显然,锐角三角函数值都是正实数,并且00,cotA>0.
4.四种三角函数的关系。
三.四种三角函数值
例1.①求出如图所示的Rt△ABC中,∠A的四个三角函数值。
解:Rt△ABC中,AB===17
∴sinA=,cosA=
tanA=,cotA= 8
②若图中AC︰BC=4︰3呢? 15
解:设AC=4,BC=3,则AB=5
∴sinA=,cosA=,tanA=,cotA=
③若图中tanA=呢?(解法同上)
例2.△ABC中,∠B=90°,a=5,b=13,求∠A的四个三角函数值。
解:Rt△ABC中,c===12
∴sinA=,cosA=,tanA=,cotA=
注意:解Rt△,如无图,应根据题意自己画图,寻找线段比值也应根据定义,不能死记公式。
四.巩固练习:
书P76 1-2
五.引申提高:
例3.如图,∠ACB=90°,CD⊥AB于D,若AD=2,BD=8。
求cosB。你还能求什么?
法一:Rt△BCD,
法二:Rt△ABC中,
变式:若AD:BD=9:16, 求∠A的四个三角函数值。 ( )
六.课时小结:
灵活运用四个三角函数求值。
七.课堂作业:
P78 习题25。2 1、2
第3课时 锐角三角函数(2)--------特殊值
教学目标:1、使学生熟记30°、45°、60°的三角函数值
2、在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
教学重点:特殊角的三角函数值。
教学过程:
1、 复习:
1.什么叫锐角A的正弦、余弦、正切、余切?
2.如图,∠C=90°,AC=7,BC=2
(1) 求∠A和∠B的四个三角函数值
(∠A: ∠B:)
(2) 比较求值结果,你发现了什么?
(sinA=cosB, cosA=sinB, tanA=cotB, cotA=tanB)
得出:如果两个锐角互余,则有
sin(90°-A)=cosA, cos(90°-A)=sinA,
tan(90°-A)=cotA, cot(90°-A)=tan A
2、 新授
1.推导特殊角的三角函数值
例1、直角△ABC中,∠A=30°,求sinA、cosA 、tanA、 cotA
由sin30°=得出:
在直角三角形中如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
练习:∠A=45°、∠A=60°呢?
归纳特殊角的三角函数值:
sin cos tan cot
30°
45° 1 1
60°
2.已知特殊角的三角函值求锐角
例2.①已知sinA=,则∠A= 30° ;
②已知tanA=1,则∠A= 45° ;
③已知cosB=,则∠B= 60° ;
④已知sinB=,则∠B= 60° ;
⑤已知则∠= 60° ;
⑥已知则∠ 75° ;
⑦已知,A,B为△ABC的内角,则∠C = 75° ;
⑧已知,则 45°或60° ;
3.计算:
例3.① ( )
② ( )
③ ( 1 )
④ ( )
3、 引申提高:
( )
注意: ①
②0<<1, 0<<1
4、 巩固练习
计算① ( )
② ( 0 )
③ ( )
④ ( 1 )
5、 课时小结
1.特殊角30°45°60°的四种三角函数值,
2.注意30°、60°角的函数值的区别
六、课作
P78 习题25。2 3、4、5
第4课时 锐角三角形函数(3)-----计算器求值
数学目标:利用计算器求出任意一个锐角的四个三角形函值;同时已知一个锐角的三角形函数值可求出这个锐角。
数学重点:利用计算器求三角函数值和锐角。
数学难点:用计数器求锐角三角函数值是要注意按键顺序。
数学过程:
一、复习提问
1、30° 、45°、60° 的三角函数值。
2、计算:1) ( )
2) ( )
3)△ABC中,求△ABC的三个内角。
二、新授
1、求已知锐角的三角函数值。
例1.求sin63°52′41″的值(精确到0.00001)
分析:由于计算器在计算角的三角函数值时,角的单位用的是度,所以我们必须先把角63°52′42″转换为″度″。
解:如下方法将角度单位状态设定为″度″:
显示
再按下列顺序依次按键:
显示结果为0.897859012
∴Sin63°52′41″≈0.8979
例2.求cot70°45 ″的值(精确到0.0001).
分析:因为计数器上无法计算余切值,于是我们根据tanA.cotA=1,
用 来计算。
解:在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:
显示结果为0.349215633.
∴cot70°45′≈0.3492.
巩固练习:
书P.111. 练习.1.
2.由锐角三角函数值求锐角.
例3. 已知tanx=0.7410. 求锐角x.(精确到1′).
解:在角度单位状态为″度″的情况下(屏幕显示出 ) ,按下列顺序依次按键:
显示结果为:36.53844577.
再按键 显示结果为36°32°18.4 .
∴x≈36°32′
注意:由角x的三角函数值求角x,按键的次序有所不同,它与求角x的三角函数值是一个“互递”的过程。
例4:已知cotx=0.7410. 求锐角x.(精确到1′)
分析:根据可以求出tanx的值.然后根据例3的方法可求出锐角x.
解:∵cotx=0.7410,
∴
三、巩固练习:
书P.77. 练习
四、课时小结。
1. 利用计数器求出任意一个锐角的四个三角函数值,同时已知一个锐角函数值可求出这个锐角。
2. 求已知锐角的余切时,应先求出正切值,再根据求出其余切值;结果应注意近似要求.
五、课作:
练习册
第5课时 锐角三角形函数(4)—复习
教学目标:熟练运用三角函数知识解题
教学重点:锐角三角函数
教学难点:锐角三角函数的运用
教学过程:
1、 复习
1. 直角三角形中四个锐角三角函数的求法
2. 特殊三角的三角函数值
2、 新授
例1.如图,菱形ABCD中,对角线AC=16,BD=30,求:①∠ABD的四个三角函数值。②sin∠ABC
解:①在菱形ABCD中,AO=CO=8,BO=DO=15,AC⊥BD,∴AB===17
在Rt△ABO中,sin∠ABD=,cos∠ABD=,tan∠ABD=,cot∠ABD=
②过C作CE⊥AB于E,菱形ABCD中,AB=BC=17,S=
∴×16×30=,∴CE=
Rt△BCE中,sin∠ABC=
例2.在△ABC中,∠C=90°,sinA=,求cosA的值
分析:本题可有两种方法求解
1. 利用∠A的正弦、余弦的定义来解
2. 利用同角三角函数中的平方关系式
解法一:设a=,c=,则b=,∴cosA=
解法二:∵sinA+cosA=1,sinA=,∴cosA=
三。引申提高:
例3.如图,在Rt△ABC中,∠ACB=90°,sinB=,D是BC上一点,
DE⊥AB于E,CD=DE,AC+CD=9,求BE、CE的长。
分析:由sinB= ,可设DE=CD= ,DB=,则BC=8,AC=6,AB=10,再由AC+CD=9,可求出各边长。在Rt△BDE中,由勾股定理求BE长,过C作CF⊥AB,再用勾股定理求解。
解:∵sinB=,∠ACB=90°,DE⊥AB,∴sinB=,设DE=CD=3,则DB=5
又CD=DE=3,∴CB=8,∴AC=6,AB=10,∵AC+CD=9,∴6,∴
∴DE=3,DB=5,∴BE=
过C作CF⊥AB于F,则CF∥DE,∴,求得CF=,BF=
∴EF=,在Rt△CEF中,
四、巩固练习
△ABC中,∠C=90°,a=40,c=41.
求的值。 ( 0 )
2.计算① ( )
② ( 1 )
3.△ABC中,AB=AC=5,BC=8,求cosB 。 ( )
五、课时小结.
1. 熟记锐角三角函数定义及特殊角的三角函数值。
2. 三角函数定义的理解在复杂图形中求某角的三角函数值。
3. 通过作垂线构造Rt△,运用勾股定理列方程求解。
六、课作:
△ABC中,,∠C= 60°
2.△ABC中,∠C=90°,斜边上的中线长为m,且,求最小角的余弦值。 ( )
△ABC中,∠ACB=90°,AC=BC,D是BC上一点,
且DC=2BD,DE⊥AB于E,求sin∠AEC的值。()
△ABC中,∠C=30°,D为AC上一点,DB⊥BC,已
知AD︰DC=1︰2,求tan∠ABD的值。 ()
△ABC中,∠C=90°,D为BC中点,DE⊥AB于E,
tanB=,AE=7,求DE长。()
第6课时 解直角三角形(1)
教学目标:利用直角三角形边角之间的关系,解决与直角三角形有关的实际问题
教学重点:解直角三角形的有关知识
教学难点:运用所学知识解决实际问题
教学过程:
1、 复习提问
1. Rt△中的关系式.(∠C=90°)
1) 角:∠A﹢∠B=90°
2) 边;a ﹢b=c
3) 边角关系:sinA= coA= tanA= cotA=
2. △ABC中,若∠C=90°,∠A=30°,c=10㎝,则a=c=5㎝,b=a=5㎝;
若∠A=40°,c=10㎝,则由sinA=,∴,由cosA=
,∴
由以知的边角关系,求得未知的边与角,叫做解直角三角形。
2、 新授
看书P78例1、例2
得出:1.解Rt△的定义;在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形。
2.解Rt△,只有下面两种情况:1)已知两条边
2)已知一条边和一个锐角
3.在解Rt△的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′。
例3. 某施工人员在离地面高度为5米的C处引拉电线杆,若固定点离电线杆3米,如图所示,则至少需要多长的缆线AC才能拉住电线杆?(结果保留两位小数)
分析:由图可知,AC是Rt△ABC的斜边,利用勾股定理就可求出。
解:在Rt△ABC中,AC===≈5.83(米)
答:至少需要5.83米的缆线AC才能拉住电线杆。
三、引申提高:
例4. 如图,上午8时,小明从电视转播塔C的正北方向B处以15千米/时的速度沿着笔直的公路出发,2小时后到达A处,测得电视转播塔在他的南偏东50°的方向,试求出发前小明与电视转播塔之间的距离,并求出此时距电视转播塔有多远?(精确到1千米)
解:在RtABC中,∠CAB=90°-50°=40°,AB=15×2=30(千米),
∵tan∠CAB=,∴≈25(千米),
∵cos∠CAB=,∴AC=≈39(千米)
答:出发前小明与电视转播塔的距离约25千米,此时距电视塔39千米。
变式: 若已知敌舰与A炮台的距离及∠DAC的读书分,如何求两炮台间的距离?
测量中能应用解直角三角形的知识吗?
四。巩固练习
P79,练习1-2
五.课时小结:
本节的重要内容是解Rt△的有关知识,解Rt△的依据是勾股定理.两锐角互余和边角之间的关系,一般有两种类型:已知两边,已知一边和一锐角,解题时要选择适当的关系式,尽可能使用原题数据和避免做除法运算。
六.课作。
P82 习题25.3 1
第7课时 解直角三角形(2)
教学目标:分清仰角、俯角等概念的意义,准确把握这些概念解决一些实际问题
教学重点:仰角、俯角、等位角等概念
教学难点:解与此有关的问题
教学过程:
1、 仰角、俯角的概念
铅垂线 几个概念 1.铅垂线
2.水平线
仰角 3.视线
俯角 4.仰角:视线在水平线的上方,视线与水平线的夹角。
5.俯角:视线在水平线的下方,视线与水平线的夹角。
练习:1.由A测得B的仰角为36°,由B去测A时的俯角为 。
2.一棵树AC在地面上的影子BC为10米,在树影一端B测得树顶A的俯角为
45°,则树高 米;若仰角为60°,树高 米。(精确到1米)
2、 应用
例1.书P80 例3
例2.如图,线段AB、CD分别表示甲、乙两幢楼,AB⊥CD,CD⊥BD,从甲楼顶A测乙楼顶C的仰角=30°,已知甲楼高15米,两楼水平距离为24米,求乙楼高。
解:Rt△ACE中,CE==8m,∴CD=CE+DE=CE+AB=(8+15)(米)
答:乙楼高为(8+15)米。
三、引申提高:
例3.如图,为了测量顶部不能达到的建筑物AB的高度,现在地平面上取一点C,用测量仪测得A点的仰角为45°,再向前进20米取一点D,使点D在BC延长线上,此时测得A的仰角为30°,已知测量仪的高为1.5米,求建筑物AB的高度。
解:在Rt△AEG中,EG==AG,在Rt△AFG中,
FG==AG∴EF=FE-EG=(-1)AG=20,
∴AG=+11.5(米)
答:建筑物AB的高度为(+11.5)米。
说明:解此类问题的关键是建立实际问题的数学模型,即构建Rt△。必要时可添加适当的辅助线,解题时应选择适当的关系式进行解题,并按照题目中的要求进行近似计算。
变式:若点E在FG的延长线上,且∠AEG=45°,已知FE的长度,其他条件不变,如何求建筑物AB的高度?
例4.如图,在一座山的山顶处用高为1米的测顶器望地面C、D两点,测得俯角分别为
60°和45°,若已知DC长为20㎝,求山高。
分析:已知∠FAD=45°,∠FAC=60°,要求山高,只需求AE。
解;设AE=,在Rt△ADE中,,
在R△ACE中,,DC=DE-CE==20,
∴,∴BE=AE-AB=29+10,
∴山高为(29+10)米。
四.巩固练习。
1. 了解仰角、俯角的概念。
2. 学会几何建模,通过解Rt△求解。
五.课作。
P82 习题25.3 2、3
第8课时 解直角三角形(3)
教学目标:弄清铅垂高度、水平长度、坡高(或坡比)、坡角等概念;
教学重点:理解坡度和坡角的概念
教学难点:利用坡度和坡角等条件,解决有关的实际问题
教学过程:
一、复习提问:
什么叫仰角、俯角?
二、坡度、坡角的概念
几个概念: 1、铅垂高度
2、水平长度
3、坡度(坡比):坡面的铅垂高度和水平长度的比
4、坡角:坡面与水平面的夹角.
显然,坡度越大,坡角就越大,坡面就越陡。
练习:1、沿山坡前进10米,相应升高5米,则山坡坡度,坡角 30°,
2、若一斜坡的坡面的余弦为,则坡度,
3、堤坝横断面是等腰梯形,(如图所示)
1 若AB=10,CD=4,高h=4,则坡度=,AD= 5
②若AB=10,CD=4 ,,则 2 ,
例1、书P81 例4
例2、如图,水库堤坝的横断面成梯形ABCD,DC∥AB,迎水坡AD长为米,上底DC长为2米,背水坡BC长也为2米,又测得∠DAB=30°,∠CBA=60°,求下底AB的长.
解:过D、C分别作DE⊥AB于E,CF⊥AB于F,
在直角△ADE中,∠A=30°,AD=
∴DE=AD sin30°=,AE=AD cos30°=3. 30° 60°
在直角△CBF中,BF=BC cos60°=1
∴AB=AE+EF+BF=3+2+1=6
答:下底的长为6米。
思考:延长两腰或平移一腰能求出下底的长吗?
说明:以上解法体现了“转化”思想,把梯形的有关问题转化为解直角三角形可多角度的分析,添加辅助线,灵活、恰当地构造直角三角形,使解法合理化。
例3.铁道路基的横断面是等腰梯形,其尺寸如图所示,其中=1:1.5是坡度每修1m长的这种路基,需要土石多少立方
解:过A、D分别作AE⊥BC于E,DF⊥BC于F.则AE=DF=1.2m.
∵=1:1.5.ABCD为等腰梯形.
∴BE=CF=1.8m
∴BC=1.8+10+1.8=13.6m
∴SABCD=㎡
∴V=1×14.16=14.16
答:需要土面14.16立方米。
三、引申提高:
例4.沿水库拦水坝的背水坡,将坝顶加宽2m,坡度由原来的1:2改为1:2.5,已知坝高6m,坝长50m,求:
1 加宽部分横断面的面积
2 完成这一工程需要的土方是多少?
分析:加宽部分的横断面AFEB为梯形,故通过
作梯形的高构造直角三角形,利用坡度的变化求解。
解:①设梯形ABCD为原大坝的横截面图,梯形AFEB为加宽部分,
过A、F分别作AG⊥BC于G,FH⊥BC于H,
在直角△ABG中,由AG=6,得BG=12
在直角△EFH中,由FH=6,得EH=15
∴EB=EH-BH=EH-(BG-HG)=15-(12-2)=5
∴SAFEB=㎡
②V=50×SAFEB=21×50=1050
四、巩固练习
P82 练习1
五、课时小结
1、 理解坡度、坡角的概念
2、 在复杂图形中求解时要结合图形,理解题意,运用所学知识通过构造直角三角形求解。
六、作业
P82 习题25.3 4
第9课时 解直角三角形(4)
教学目标:综合运用前面所学的知识,通过添加适当的辅助线来构造Rt△,从而解决较复杂的实际问题。
教学重点难点:利用前面所学知识,解决教复杂的实际问题
教学过程:
一、复习、练习
1.Rt△ABC中,∠C=90°,CD⊥AB于D,若AD=2,CD=4,则tanB=
2.Rt△ABC中,∠A=90°,sinB=,c=2,则b=
3.Rt△ABC中,∠C=90°,斜边上中线CD=3,AC=3.6,tan∠DCB=
二、应用
例1. 如图△ABC中,∠B=45°,∠C=60,AD⊥BC于D,AD=2,
求:(1)BC的长 (2)S
解:(1)∵AD⊥BC,∠B=45°,∠C=60°,AD=2
∴BD=2,CD= ∴BC=2+
(2)∴S=×2×(2+)=2+
例2. 如图,为调整数学格局,充分发挥资源优势,现将地处A、B两地的两所技校合并成职业技术教育中心,为方便A、B两校师生的交往,学校准备在相距5千米的A、B两地修筑一条笔直公路AB,经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为1.8千米的湖泊,问计划修筑的这条公路会不会穿过湖泊?
分析:要想知道公路会不会穿过湖泊,就必须知道点C到AB的距离是否大于1.8千米。
解:过C作CD⊥AB于D
由题意知∠CAD=30°,在Rt△ACD中,AD=,在Rt△BCD中,同理可得CD=DB,∴AB=AD+BD=(+1)CD=5,∴CD≈1.84(千米)>1.8千米
答:计划修筑的这条公路不会穿过湖泊。
例3. 如图,河对岸有一电线杆CD,从A点测得电线杆顶端的仰角为18°,前进30米,到B处测得D点的仰角为36°,求电线杆的高度(精确到0.1米)
解:∵∠ADB=∠DBC-∠A=36°-18°=18°=∠A,∴DB=AB=30,
在Rt△ABC中,CD=≈17.6(米)
答:电线杆的高度约为17.6米。
三、引申提高:
例4. 如图,A城气象部门测得今年第9号台风上午8时在A城南偏东30°的海面生成,并以每小时40海里的速度向正北方向移动,上午10时测得台风中心移到了A城南偏东45°的方向,若台风中心120海里的范围内将受台风影响,问A城是否会受9号台风影响?
分析:A城是否会受台风影响,就是A城到台风移动路线BC的距离是否大于120千米。
解:过A作AE⊥BC于E,设AE=EC=,则BE=,
∵BC=2×40=80,∴BC=BE-CE=(-1)=80,
∴≈109.2<120,
∴A城会受台风影响。
三、巩固练习
P85, 6,7,8
四、课时小结
运用所学知识解决实际问题,学会几何建模,通过解Rt△求解
五、课作
P86, 11,12,13
第10课时. 解直角三角形小结与复习(1)
数学目标:1、正确运用勾股定理
2、掌握三角函数定义,正确运用直角三角形边角关系
3、理解实际问题的相关概念
教学过程:
一、复习
知识结构与学习要点;书P.84
二、练习:
(一).1.Rt△中一直角边为7,三边长都为正整数,则周长为 53
2. Rt△中,斜边上中线为1,周长为, 则面积为
3. Rt△中,两边长为2, 4. 则第三边长为或
(二)1.一Rt△被斜边上的高分得的两个三角形面积之比为4:9,则Rt△中最小角的正切为 ,
2. Rt△ABC中,∠C=90°,sinA=则 4 , 6 ,
3.如图△ABC中,∠B=60°,AD=14,CD=12,S△ADC=,求BD;
解;S△ADC= ∴
Rt△AED中, Rt△ABE中,
∴
4.△ABC中.AD⊥BC,M为BA中点,∠B=30°,cos∠ACD=,求tan∠BCM。
解:设则,
∵为中点 ∴
5.计算或化简:
① ( )
②(45°<<90° ()
(三).1.甲、乙两人与一路灯站在一直线上,从甲处看路灯顶部仰角为 ,从乙处看路灯顶部仰角 ,若路灯高h米,求甲、乙两人相距多少米?
分析:应考虑两种情况:
1) 路灯在线段BC上,BC=h()
2)路灯在线段BC延长线上,BC=h()
2、一登山运动员在山脚C处仰望山顶B,仰角 =45°.他沿坡比为的坡面走了1000m到达D处,此时仰角,则山高多少米?
略解:Rt△CDF中米,米
设,在Rt△BDE中,
∵∠BCA=45°,∴AC=AB ∴ ∴米
三、课作:
P.85. A组1——5.
第11课时 解直角三角形小结与复习(2)
数学目标:熟练运用直角三角形边角关系解决相关问题.
教学过程:
一、复习:
计算:
(1) ( 1 )
(2) ( 1 )
(3) ()
(4) ( )
(5) 求 ( 0 )
二、应用举例:
1、如图∠ACB=90°.CD⊥AB于D.
1)∠A=30°.求 ( )
2)若∠BCD=30°,AC=6. 求DB长 ( )
2.在坡度为1:2的山坡上种树,要求株距(两树间的水平距离)为6m,则相邻两树间的实际距离为多少?( )
3、一长为2.5m的梯子AB下端B与墙角O的距离1.5m,如滑动后停在DE位置,测得BD=0.5m。求梯子下落距离。
解:在Rt△ABO中.AB=2.5m. BO=1.5m. ∴AO=2m.
在Rt△DEO中.DO=2m. ED=2.5m. ∴EO=1.5m
∴AE=AO-EO=2-1.5=0.5.
∴梯子下落0.5m.
4、将截面为等腰梯形的沙河改造,使两坡度由1:0.5变为1:1,已知河道深7m,长90m,求完成这一工程挖土多少方?
解:设ABCD为原截面,EBCF为改造后的截面.
∵ ∴
∵ ∴
S=2S△ABE=2××3.5×7=24.5㎡
5、△ABC中.∠C=90°.D在B、C上 .DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BC=3cm。求;(1)Sin∠DAE. (2)cos∠B(3)S△ABD.
解:设则
由△BDE∽△DAC 得
得 得(舍)
∴sin∠ADE=COS∠B= S△ABD=13
6、如图:平面镜EF的同侧有相距 ㎝的A.B两点,它们与平面镜距离分别为5cm、7cm.现要从A点射出的垂线经平面镜反射出后通过点B,求出光线的投射角。
解:过A作AM⊥BF于M,则
∴
在Rt△AOE中, ,
∴ ∴ 即投射角为30°
三、课作
.P86. B组9—10, B组14—16,
1
DDDD
MODE
MODE
=
0 1 11
41
0 1 11
52
0 1 11
63
Sin
D
=
0 1 11
45
0 1 11
70
tan
÷
1
=
0
1
4
7
.
Tan-1
SHIFT
0
D
0 1 11
SHITFT
第1课时 测量
教学目标:利用前面学习的相似三角形的有关知识,探索测量距离的几种方法,初步接触直角三角形的边角关系。
教学重点:探索测量距离的几种方法。
教学难点:选择适当的方法测量物体的高度或长度。
教学过程:
一。复习引入:
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许想知道操场旗杆有多高?我们知道可以利用相似三角形的对应边,首先请同学量出太阳下自己的影子长度,旗杆的影子长度,再根据自己的身高,计算出旗杆的高度。如果在阴天,你一个人能测量出旗杆的高度吗?
二。新课探究:
例1. 书.P.98试一试.
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1米。现在请你按1:500的比例得△ABC画在纸上,并记为△A1B1C1,用刻度尺量出纸上B1C1的长度,便可以算出旗杆的实际高度。你知道计算的方法吗?
解:∵△ABC∽△A1B2C3, ∴AC:A1C1=BC:B1C1=500:1
∴只要用刻度尺量出纸上B1C1的长度,就可以计算出BC的长度,加上AD长即为旗杆的高度。若量得B1C1=a㎝,则BC=500a㎝=5a㎝。故旗杆高(1+5a)m.
说明:利用相似三角形的性质测量物体高度或宽度时,关键是构造和实物相似的三角形,且能直接测量出这个三角形各条线段的长,再列式计算出实物的高或宽等。
例2.为了测出旗杆的高度,设计了如图所示的三种方案,并测得图(a)中BO=6m,OD=3.4m,CD=1.7m图(b)中CD=1m,FD=0.6m,EB=1.8m图(c)中BD=9m,EF=0.2;此人的臂长为0.6m。
(1) 说明其中运用的主要知识;(2)分别计算出旗杆的高度。
(a) (b) (c)
分析:图(a)和图(c)都运用了相似三角形对应边成比例的性质,图(b)运用了同一时刻的物高与影长成正比的性质。
解:(1)∵△AOB∽△COD,∴ 即 ∴AB=3(m).
(2)∵同一时刻物高与影长成正比,∴ 即 ∴AB=3(m).
(3)∵△CEF∽△CAB ∴ 即 ∴AB=3(m).
方法技巧:测量物体的高度可利用自己的身高、臂长等长度结合相似形的性质求出物高,也可以运用同一时刻的物高与影长成正比的性质测量物体的高度。
三、引申提高:
例3。设计一种方案,测量学校科技楼的高度。请写出测量的过程,并简要说明这样做的理由。
分析:测量大楼的高度的方法很多,现采用一种方法,利用人的身高和标杆,依据相似三角形三角对应成比例和平行线的性质,可测出大楼的高度。
解答:测量过程如下:
1、在地面上立一个标杆,使人眼、杆顶、楼顶在一条直线上。
2、测出CF、CH的距离。
大楼 3、算出KE的长度。
4、用标杆长度减去人的身高,即DE的长度。
标杆 5、由DE∥AB得△KDE∽△KAB。又因为相似三角形三边对应成比例,∴。
6、再将刚才测量的数值代入比例式中,计算出AB的长度。
7、用AB加上人的身高即得出大楼的高度。
探究点拔:1.选择测量的方法应是切实可行的。如本题中人眼、杆顶、楼顶在一条直线上(人是站立的)。
2.大楼的高度=AB+人高。
3.测量的过程要清楚,力求每步都有根有据,达到学以至用。
四.巩固练习:
1.如图1,要测量A、B两点间距离,在O点设桩,取OA中点C,OB中点D,测得CD=31.4m 求AB长。 (AB=62.8m)
(1) (2)
2. 如图2, 为了测量河的宽度,可以先在河对岸找到一个具有明显标志的点A,再在所在的一边找到两点B、C,使△ABC构成Rt△。如果测得BC=50米,∠ABC=73°,试设计一种方法求河的宽度AC。 (在地面上另作 Rt△A’B’C’,使B’C’=5米,∠C’=Rt∠,∠B’=73°, 测得 A’C’=16.35米,得 AC=16.35米 ).
五.课时小结:
选择适当的方法测量物体的高度或长度等是新时期素质教育的要求,运用所学相似三角形知识设计测量方案时一定要考虑可行性,力求操作简便,计算简洁,同时注意分析环境、天气等要素。
六.课堂作业:
P.73 习题25.1 1、2、3
第2课时 锐角三角函数(1)
教学目标:1.直角三角形可简记为Rt△ABC
2.理解Rt△中锐角的正弦、余弦、正切、余切的概念。
教学重点:四种锐角三角函数的定义。
教学难点:理解锐角三角函数的定义。
教学过程:
一.复习提问:
1. 什么叫Rt△?它的三边有何关系?
2.Rt△中角、边之间的关系是:①∠A+∠B=90°②
二.新课探究:
1.Rt△ABC中,某个角的对边、邻边的介绍。
2.如图,由Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
得
可见,在Rt△ABC中,对于锐角A的每一
个确定的值,其对边与邻边的比值是惟一确定的。
同样,其对边与斜边,邻边与斜边,邻边与对边的比值也是惟一确定的。
3.四种锐角三角函数。
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
显然,锐角三角函数值都是正实数,并且0
4.四种三角函数的关系。
三.四种三角函数值
例1.①求出如图所示的Rt△ABC中,∠A的四个三角函数值。
解:Rt△ABC中,AB===17
∴sinA=,cosA=
tanA=,cotA= 8
②若图中AC︰BC=4︰3呢? 15
解:设AC=4,BC=3,则AB=5
∴sinA=,cosA=,tanA=,cotA=
③若图中tanA=呢?(解法同上)
例2.△ABC中,∠B=90°,a=5,b=13,求∠A的四个三角函数值。
解:Rt△ABC中,c===12
∴sinA=,cosA=,tanA=,cotA=
注意:解Rt△,如无图,应根据题意自己画图,寻找线段比值也应根据定义,不能死记公式。
四.巩固练习:
书P76 1-2
五.引申提高:
例3.如图,∠ACB=90°,CD⊥AB于D,若AD=2,BD=8。
求cosB。你还能求什么?
法一:Rt△BCD,
法二:Rt△ABC中,
变式:若AD:BD=9:16, 求∠A的四个三角函数值。 ( )
六.课时小结:
灵活运用四个三角函数求值。
七.课堂作业:
P78 习题25。2 1、2
第3课时 锐角三角函数(2)--------特殊值
教学目标:1、使学生熟记30°、45°、60°的三角函数值
2、在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
教学重点:特殊角的三角函数值。
教学过程:
1、 复习:
1.什么叫锐角A的正弦、余弦、正切、余切?
2.如图,∠C=90°,AC=7,BC=2
(1) 求∠A和∠B的四个三角函数值
(∠A: ∠B:)
(2) 比较求值结果,你发现了什么?
(sinA=cosB, cosA=sinB, tanA=cotB, cotA=tanB)
得出:如果两个锐角互余,则有
sin(90°-A)=cosA, cos(90°-A)=sinA,
tan(90°-A)=cotA, cot(90°-A)=tan A
2、 新授
1.推导特殊角的三角函数值
例1、直角△ABC中,∠A=30°,求sinA、cosA 、tanA、 cotA
由sin30°=得出:
在直角三角形中如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
练习:∠A=45°、∠A=60°呢?
归纳特殊角的三角函数值:
sin cos tan cot
30°
45° 1 1
60°
2.已知特殊角的三角函值求锐角
例2.①已知sinA=,则∠A= 30° ;
②已知tanA=1,则∠A= 45° ;
③已知cosB=,则∠B= 60° ;
④已知sinB=,则∠B= 60° ;
⑤已知则∠= 60° ;
⑥已知则∠ 75° ;
⑦已知,A,B为△ABC的内角,则∠C = 75° ;
⑧已知,则 45°或60° ;
3.计算:
例3.① ( )
② ( )
③ ( 1 )
④ ( )
3、 引申提高:
( )
注意: ①
②0<<1, 0<<1
4、 巩固练习
计算① ( )
② ( 0 )
③ ( )
④ ( 1 )
5、 课时小结
1.特殊角30°45°60°的四种三角函数值,
2.注意30°、60°角的函数值的区别
六、课作
P78 习题25。2 3、4、5
第4课时 锐角三角形函数(3)-----计算器求值
数学目标:利用计算器求出任意一个锐角的四个三角形函值;同时已知一个锐角的三角形函数值可求出这个锐角。
数学重点:利用计算器求三角函数值和锐角。
数学难点:用计数器求锐角三角函数值是要注意按键顺序。
数学过程:
一、复习提问
1、30° 、45°、60° 的三角函数值。
2、计算:1) ( )
2) ( )
3)△ABC中,求△ABC的三个内角。
二、新授
1、求已知锐角的三角函数值。
例1.求sin63°52′41″的值(精确到0.00001)
分析:由于计算器在计算角的三角函数值时,角的单位用的是度,所以我们必须先把角63°52′42″转换为″度″。
解:如下方法将角度单位状态设定为″度″:
显示
再按下列顺序依次按键:
显示结果为0.897859012
∴Sin63°52′41″≈0.8979
例2.求cot70°45 ″的值(精确到0.0001).
分析:因为计数器上无法计算余切值,于是我们根据tanA.cotA=1,
用 来计算。
解:在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:
显示结果为0.349215633.
∴cot70°45′≈0.3492.
巩固练习:
书P.111. 练习.1.
2.由锐角三角函数值求锐角.
例3. 已知tanx=0.7410. 求锐角x.(精确到1′).
解:在角度单位状态为″度″的情况下(屏幕显示出 ) ,按下列顺序依次按键:
显示结果为:36.53844577.
再按键 显示结果为36°32°18.4 .
∴x≈36°32′
注意:由角x的三角函数值求角x,按键的次序有所不同,它与求角x的三角函数值是一个“互递”的过程。
例4:已知cotx=0.7410. 求锐角x.(精确到1′)
分析:根据可以求出tanx的值.然后根据例3的方法可求出锐角x.
解:∵cotx=0.7410,
∴
三、巩固练习:
书P.77. 练习
四、课时小结。
1. 利用计数器求出任意一个锐角的四个三角函数值,同时已知一个锐角函数值可求出这个锐角。
2. 求已知锐角的余切时,应先求出正切值,再根据求出其余切值;结果应注意近似要求.
五、课作:
练习册
第5课时 锐角三角形函数(4)—复习
教学目标:熟练运用三角函数知识解题
教学重点:锐角三角函数
教学难点:锐角三角函数的运用
教学过程:
1、 复习
1. 直角三角形中四个锐角三角函数的求法
2. 特殊三角的三角函数值
2、 新授
例1.如图,菱形ABCD中,对角线AC=16,BD=30,求:①∠ABD的四个三角函数值。②sin∠ABC
解:①在菱形ABCD中,AO=CO=8,BO=DO=15,AC⊥BD,∴AB===17
在Rt△ABO中,sin∠ABD=,cos∠ABD=,tan∠ABD=,cot∠ABD=
②过C作CE⊥AB于E,菱形ABCD中,AB=BC=17,S=
∴×16×30=,∴CE=
Rt△BCE中,sin∠ABC=
例2.在△ABC中,∠C=90°,sinA=,求cosA的值
分析:本题可有两种方法求解
1. 利用∠A的正弦、余弦的定义来解
2. 利用同角三角函数中的平方关系式
解法一:设a=,c=,则b=,∴cosA=
解法二:∵sinA+cosA=1,sinA=,∴cosA=
三。引申提高:
例3.如图,在Rt△ABC中,∠ACB=90°,sinB=,D是BC上一点,
DE⊥AB于E,CD=DE,AC+CD=9,求BE、CE的长。
分析:由sinB= ,可设DE=CD= ,DB=,则BC=8,AC=6,AB=10,再由AC+CD=9,可求出各边长。在Rt△BDE中,由勾股定理求BE长,过C作CF⊥AB,再用勾股定理求解。
解:∵sinB=,∠ACB=90°,DE⊥AB,∴sinB=,设DE=CD=3,则DB=5
又CD=DE=3,∴CB=8,∴AC=6,AB=10,∵AC+CD=9,∴6,∴
∴DE=3,DB=5,∴BE=
过C作CF⊥AB于F,则CF∥DE,∴,求得CF=,BF=
∴EF=,在Rt△CEF中,
四、巩固练习
△ABC中,∠C=90°,a=40,c=41.
求的值。 ( 0 )
2.计算① ( )
② ( 1 )
3.△ABC中,AB=AC=5,BC=8,求cosB 。 ( )
五、课时小结.
1. 熟记锐角三角函数定义及特殊角的三角函数值。
2. 三角函数定义的理解在复杂图形中求某角的三角函数值。
3. 通过作垂线构造Rt△,运用勾股定理列方程求解。
六、课作:
△ABC中,,∠C= 60°
2.△ABC中,∠C=90°,斜边上的中线长为m,且,求最小角的余弦值。 ( )
△ABC中,∠ACB=90°,AC=BC,D是BC上一点,
且DC=2BD,DE⊥AB于E,求sin∠AEC的值。()
△ABC中,∠C=30°,D为AC上一点,DB⊥BC,已
知AD︰DC=1︰2,求tan∠ABD的值。 ()
△ABC中,∠C=90°,D为BC中点,DE⊥AB于E,
tanB=,AE=7,求DE长。()
第6课时 解直角三角形(1)
教学目标:利用直角三角形边角之间的关系,解决与直角三角形有关的实际问题
教学重点:解直角三角形的有关知识
教学难点:运用所学知识解决实际问题
教学过程:
1、 复习提问
1. Rt△中的关系式.(∠C=90°)
1) 角:∠A﹢∠B=90°
2) 边;a ﹢b=c
3) 边角关系:sinA= coA= tanA= cotA=
2. △ABC中,若∠C=90°,∠A=30°,c=10㎝,则a=c=5㎝,b=a=5㎝;
若∠A=40°,c=10㎝,则由sinA=,∴,由cosA=
,∴
由以知的边角关系,求得未知的边与角,叫做解直角三角形。
2、 新授
看书P78例1、例2
得出:1.解Rt△的定义;在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形。
2.解Rt△,只有下面两种情况:1)已知两条边
2)已知一条边和一个锐角
3.在解Rt△的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′。
例3. 某施工人员在离地面高度为5米的C处引拉电线杆,若固定点离电线杆3米,如图所示,则至少需要多长的缆线AC才能拉住电线杆?(结果保留两位小数)
分析:由图可知,AC是Rt△ABC的斜边,利用勾股定理就可求出。
解:在Rt△ABC中,AC===≈5.83(米)
答:至少需要5.83米的缆线AC才能拉住电线杆。
三、引申提高:
例4. 如图,上午8时,小明从电视转播塔C的正北方向B处以15千米/时的速度沿着笔直的公路出发,2小时后到达A处,测得电视转播塔在他的南偏东50°的方向,试求出发前小明与电视转播塔之间的距离,并求出此时距电视转播塔有多远?(精确到1千米)
解:在RtABC中,∠CAB=90°-50°=40°,AB=15×2=30(千米),
∵tan∠CAB=,∴≈25(千米),
∵cos∠CAB=,∴AC=≈39(千米)
答:出发前小明与电视转播塔的距离约25千米,此时距电视塔39千米。
变式: 若已知敌舰与A炮台的距离及∠DAC的读书分,如何求两炮台间的距离?
测量中能应用解直角三角形的知识吗?
四。巩固练习
P79,练习1-2
五.课时小结:
本节的重要内容是解Rt△的有关知识,解Rt△的依据是勾股定理.两锐角互余和边角之间的关系,一般有两种类型:已知两边,已知一边和一锐角,解题时要选择适当的关系式,尽可能使用原题数据和避免做除法运算。
六.课作。
P82 习题25.3 1
第7课时 解直角三角形(2)
教学目标:分清仰角、俯角等概念的意义,准确把握这些概念解决一些实际问题
教学重点:仰角、俯角、等位角等概念
教学难点:解与此有关的问题
教学过程:
1、 仰角、俯角的概念
铅垂线 几个概念 1.铅垂线
2.水平线
仰角 3.视线
俯角 4.仰角:视线在水平线的上方,视线与水平线的夹角。
5.俯角:视线在水平线的下方,视线与水平线的夹角。
练习:1.由A测得B的仰角为36°,由B去测A时的俯角为 。
2.一棵树AC在地面上的影子BC为10米,在树影一端B测得树顶A的俯角为
45°,则树高 米;若仰角为60°,树高 米。(精确到1米)
2、 应用
例1.书P80 例3
例2.如图,线段AB、CD分别表示甲、乙两幢楼,AB⊥CD,CD⊥BD,从甲楼顶A测乙楼顶C的仰角=30°,已知甲楼高15米,两楼水平距离为24米,求乙楼高。
解:Rt△ACE中,CE==8m,∴CD=CE+DE=CE+AB=(8+15)(米)
答:乙楼高为(8+15)米。
三、引申提高:
例3.如图,为了测量顶部不能达到的建筑物AB的高度,现在地平面上取一点C,用测量仪测得A点的仰角为45°,再向前进20米取一点D,使点D在BC延长线上,此时测得A的仰角为30°,已知测量仪的高为1.5米,求建筑物AB的高度。
解:在Rt△AEG中,EG==AG,在Rt△AFG中,
FG==AG∴EF=FE-EG=(-1)AG=20,
∴AG=+11.5(米)
答:建筑物AB的高度为(+11.5)米。
说明:解此类问题的关键是建立实际问题的数学模型,即构建Rt△。必要时可添加适当的辅助线,解题时应选择适当的关系式进行解题,并按照题目中的要求进行近似计算。
变式:若点E在FG的延长线上,且∠AEG=45°,已知FE的长度,其他条件不变,如何求建筑物AB的高度?
例4.如图,在一座山的山顶处用高为1米的测顶器望地面C、D两点,测得俯角分别为
60°和45°,若已知DC长为20㎝,求山高。
分析:已知∠FAD=45°,∠FAC=60°,要求山高,只需求AE。
解;设AE=,在Rt△ADE中,,
在R△ACE中,,DC=DE-CE==20,
∴,∴BE=AE-AB=29+10,
∴山高为(29+10)米。
四.巩固练习。
1. 了解仰角、俯角的概念。
2. 学会几何建模,通过解Rt△求解。
五.课作。
P82 习题25.3 2、3
第8课时 解直角三角形(3)
教学目标:弄清铅垂高度、水平长度、坡高(或坡比)、坡角等概念;
教学重点:理解坡度和坡角的概念
教学难点:利用坡度和坡角等条件,解决有关的实际问题
教学过程:
一、复习提问:
什么叫仰角、俯角?
二、坡度、坡角的概念
几个概念: 1、铅垂高度
2、水平长度
3、坡度(坡比):坡面的铅垂高度和水平长度的比
4、坡角:坡面与水平面的夹角.
显然,坡度越大,坡角就越大,坡面就越陡。
练习:1、沿山坡前进10米,相应升高5米,则山坡坡度,坡角 30°,
2、若一斜坡的坡面的余弦为,则坡度,
3、堤坝横断面是等腰梯形,(如图所示)
1 若AB=10,CD=4,高h=4,则坡度=,AD= 5
②若AB=10,CD=4 ,,则 2 ,
例1、书P81 例4
例2、如图,水库堤坝的横断面成梯形ABCD,DC∥AB,迎水坡AD长为米,上底DC长为2米,背水坡BC长也为2米,又测得∠DAB=30°,∠CBA=60°,求下底AB的长.
解:过D、C分别作DE⊥AB于E,CF⊥AB于F,
在直角△ADE中,∠A=30°,AD=
∴DE=AD sin30°=,AE=AD cos30°=3. 30° 60°
在直角△CBF中,BF=BC cos60°=1
∴AB=AE+EF+BF=3+2+1=6
答:下底的长为6米。
思考:延长两腰或平移一腰能求出下底的长吗?
说明:以上解法体现了“转化”思想,把梯形的有关问题转化为解直角三角形可多角度的分析,添加辅助线,灵活、恰当地构造直角三角形,使解法合理化。
例3.铁道路基的横断面是等腰梯形,其尺寸如图所示,其中=1:1.5是坡度每修1m长的这种路基,需要土石多少立方
解:过A、D分别作AE⊥BC于E,DF⊥BC于F.则AE=DF=1.2m.
∵=1:1.5.ABCD为等腰梯形.
∴BE=CF=1.8m
∴BC=1.8+10+1.8=13.6m
∴SABCD=㎡
∴V=1×14.16=14.16
答:需要土面14.16立方米。
三、引申提高:
例4.沿水库拦水坝的背水坡,将坝顶加宽2m,坡度由原来的1:2改为1:2.5,已知坝高6m,坝长50m,求:
1 加宽部分横断面的面积
2 完成这一工程需要的土方是多少?
分析:加宽部分的横断面AFEB为梯形,故通过
作梯形的高构造直角三角形,利用坡度的变化求解。
解:①设梯形ABCD为原大坝的横截面图,梯形AFEB为加宽部分,
过A、F分别作AG⊥BC于G,FH⊥BC于H,
在直角△ABG中,由AG=6,得BG=12
在直角△EFH中,由FH=6,得EH=15
∴EB=EH-BH=EH-(BG-HG)=15-(12-2)=5
∴SAFEB=㎡
②V=50×SAFEB=21×50=1050
四、巩固练习
P82 练习1
五、课时小结
1、 理解坡度、坡角的概念
2、 在复杂图形中求解时要结合图形,理解题意,运用所学知识通过构造直角三角形求解。
六、作业
P82 习题25.3 4
第9课时 解直角三角形(4)
教学目标:综合运用前面所学的知识,通过添加适当的辅助线来构造Rt△,从而解决较复杂的实际问题。
教学重点难点:利用前面所学知识,解决教复杂的实际问题
教学过程:
一、复习、练习
1.Rt△ABC中,∠C=90°,CD⊥AB于D,若AD=2,CD=4,则tanB=
2.Rt△ABC中,∠A=90°,sinB=,c=2,则b=
3.Rt△ABC中,∠C=90°,斜边上中线CD=3,AC=3.6,tan∠DCB=
二、应用
例1. 如图△ABC中,∠B=45°,∠C=60,AD⊥BC于D,AD=2,
求:(1)BC的长 (2)S
解:(1)∵AD⊥BC,∠B=45°,∠C=60°,AD=2
∴BD=2,CD= ∴BC=2+
(2)∴S=×2×(2+)=2+
例2. 如图,为调整数学格局,充分发挥资源优势,现将地处A、B两地的两所技校合并成职业技术教育中心,为方便A、B两校师生的交往,学校准备在相距5千米的A、B两地修筑一条笔直公路AB,经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为1.8千米的湖泊,问计划修筑的这条公路会不会穿过湖泊?
分析:要想知道公路会不会穿过湖泊,就必须知道点C到AB的距离是否大于1.8千米。
解:过C作CD⊥AB于D
由题意知∠CAD=30°,在Rt△ACD中,AD=,在Rt△BCD中,同理可得CD=DB,∴AB=AD+BD=(+1)CD=5,∴CD≈1.84(千米)>1.8千米
答:计划修筑的这条公路不会穿过湖泊。
例3. 如图,河对岸有一电线杆CD,从A点测得电线杆顶端的仰角为18°,前进30米,到B处测得D点的仰角为36°,求电线杆的高度(精确到0.1米)
解:∵∠ADB=∠DBC-∠A=36°-18°=18°=∠A,∴DB=AB=30,
在Rt△ABC中,CD=≈17.6(米)
答:电线杆的高度约为17.6米。
三、引申提高:
例4. 如图,A城气象部门测得今年第9号台风上午8时在A城南偏东30°的海面生成,并以每小时40海里的速度向正北方向移动,上午10时测得台风中心移到了A城南偏东45°的方向,若台风中心120海里的范围内将受台风影响,问A城是否会受9号台风影响?
分析:A城是否会受台风影响,就是A城到台风移动路线BC的距离是否大于120千米。
解:过A作AE⊥BC于E,设AE=EC=,则BE=,
∵BC=2×40=80,∴BC=BE-CE=(-1)=80,
∴≈109.2<120,
∴A城会受台风影响。
三、巩固练习
P85, 6,7,8
四、课时小结
运用所学知识解决实际问题,学会几何建模,通过解Rt△求解
五、课作
P86, 11,12,13
第10课时. 解直角三角形小结与复习(1)
数学目标:1、正确运用勾股定理
2、掌握三角函数定义,正确运用直角三角形边角关系
3、理解实际问题的相关概念
教学过程:
一、复习
知识结构与学习要点;书P.84
二、练习:
(一).1.Rt△中一直角边为7,三边长都为正整数,则周长为 53
2. Rt△中,斜边上中线为1,周长为, 则面积为
3. Rt△中,两边长为2, 4. 则第三边长为或
(二)1.一Rt△被斜边上的高分得的两个三角形面积之比为4:9,则Rt△中最小角的正切为 ,
2. Rt△ABC中,∠C=90°,sinA=则 4 , 6 ,
3.如图△ABC中,∠B=60°,AD=14,CD=12,S△ADC=,求BD;
解;S△ADC= ∴
Rt△AED中, Rt△ABE中,
∴
4.△ABC中.AD⊥BC,M为BA中点,∠B=30°,cos∠ACD=,求tan∠BCM。
解:设则,
∵为中点 ∴
5.计算或化简:
① ( )
②(45°<<90° ()
(三).1.甲、乙两人与一路灯站在一直线上,从甲处看路灯顶部仰角为 ,从乙处看路灯顶部仰角 ,若路灯高h米,求甲、乙两人相距多少米?
分析:应考虑两种情况:
1) 路灯在线段BC上,BC=h()
2)路灯在线段BC延长线上,BC=h()
2、一登山运动员在山脚C处仰望山顶B,仰角 =45°.他沿坡比为的坡面走了1000m到达D处,此时仰角,则山高多少米?
略解:Rt△CDF中米,米
设,在Rt△BDE中,
∵∠BCA=45°,∴AC=AB ∴ ∴米
三、课作:
P.85. A组1——5.
第11课时 解直角三角形小结与复习(2)
数学目标:熟练运用直角三角形边角关系解决相关问题.
教学过程:
一、复习:
计算:
(1) ( 1 )
(2) ( 1 )
(3) ()
(4) ( )
(5) 求 ( 0 )
二、应用举例:
1、如图∠ACB=90°.CD⊥AB于D.
1)∠A=30°.求 ( )
2)若∠BCD=30°,AC=6. 求DB长 ( )
2.在坡度为1:2的山坡上种树,要求株距(两树间的水平距离)为6m,则相邻两树间的实际距离为多少?( )
3、一长为2.5m的梯子AB下端B与墙角O的距离1.5m,如滑动后停在DE位置,测得BD=0.5m。求梯子下落距离。
解:在Rt△ABO中.AB=2.5m. BO=1.5m. ∴AO=2m.
在Rt△DEO中.DO=2m. ED=2.5m. ∴EO=1.5m
∴AE=AO-EO=2-1.5=0.5.
∴梯子下落0.5m.
4、将截面为等腰梯形的沙河改造,使两坡度由1:0.5变为1:1,已知河道深7m,长90m,求完成这一工程挖土多少方?
解:设ABCD为原截面,EBCF为改造后的截面.
∵ ∴
∵ ∴
S=2S△ABE=2××3.5×7=24.5㎡
5、△ABC中.∠C=90°.D在B、C上 .DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BC=3cm。求;(1)Sin∠DAE. (2)cos∠B(3)S△ABD.
解:设则
由△BDE∽△DAC 得
得 得(舍)
∴sin∠ADE=COS∠B= S△ABD=13
6、如图:平面镜EF的同侧有相距 ㎝的A.B两点,它们与平面镜距离分别为5cm、7cm.现要从A点射出的垂线经平面镜反射出后通过点B,求出光线的投射角。
解:过A作AM⊥BF于M,则
∴
在Rt△AOE中, ,
∴ ∴ 即投射角为30°
三、课作
.P86. B组9—10, B组14—16,
1
DDDD
MODE
MODE
=
0 1 11
41
0 1 11
52
0 1 11
63
Sin
D
=
0 1 11
45
0 1 11
70
tan
÷
1
=
0
1
4
7
.
Tan-1
SHIFT
0
D
0 1 11
SHITFT
