1.3.1 有理数的加法 课件(共25张PPT) 2023--2024学年人教版七年级数学上册
文档属性
| 名称 | 1.3.1 有理数的加法 课件(共25张PPT) 2023--2024学年人教版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 713.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 21:17:32 | ||
图片预览






文档简介
(共25张PPT)
人教版七年级数学上册
1.3.1 有理数的加法
(一)
学习目标
1.掌握有理数加法的运算律.
2. 灵活运用运算律进行有理数的加法运算.
3.会用有理数的加法解决实际问题.
(二)
自学检测
计算:
(1)(–83)+(+26)+(–17)+(–26)+(+15).
(2)
(3)
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为
用字母表示为
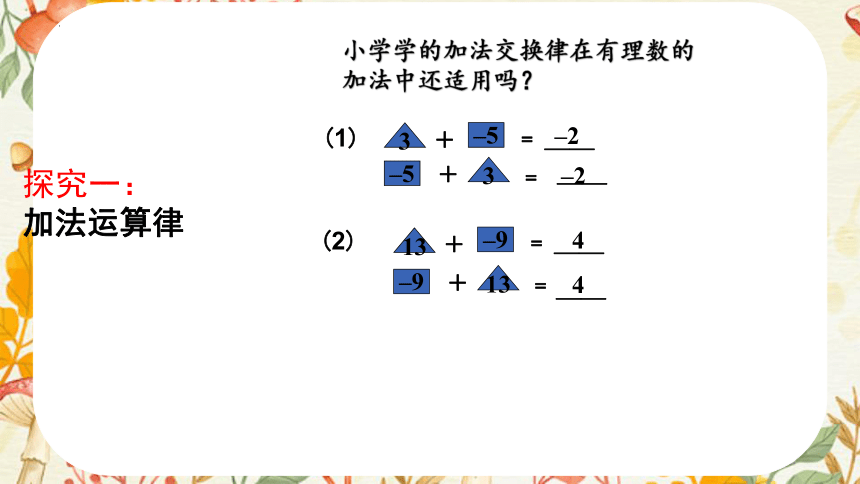
探究一:
加法运算律
3
﹢
–5
﹦
__
–2
–5
3
﹢
﹦
__
–2
13
﹢
–9
﹦
__
4
–9
13
﹢
﹦
__
4
(2)
(1)
小学学的加法交换律在有理数的加法中还适用吗?
5+3=8
①
(-5)+(-3)=-8
②
互动新授
从算式①②中,你发现了什么呢?
算式①②都是同号相加.
那你能概括出运算规律吗?
符号相同的两个数相加,结果的符号不变,绝对值相加.
互动新授
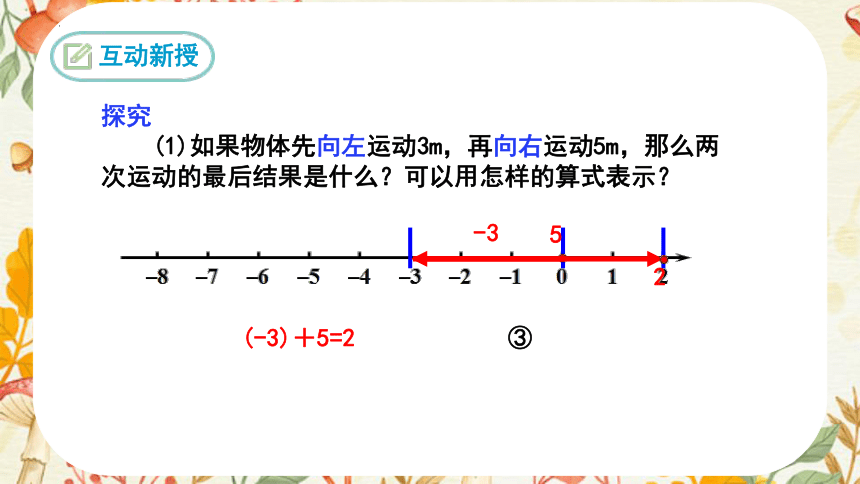
探究
(1)如果物体先向左运动3m,再向右运动5m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
5
2
(-3)+5=2 ③
有
法
的
理
数
加
例 2
已知|a|=2,|b|=3,求a+b的值.
∵|a|=2,|b|=3,∴a=±2,b=±3
∴当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5
解:
互动新授
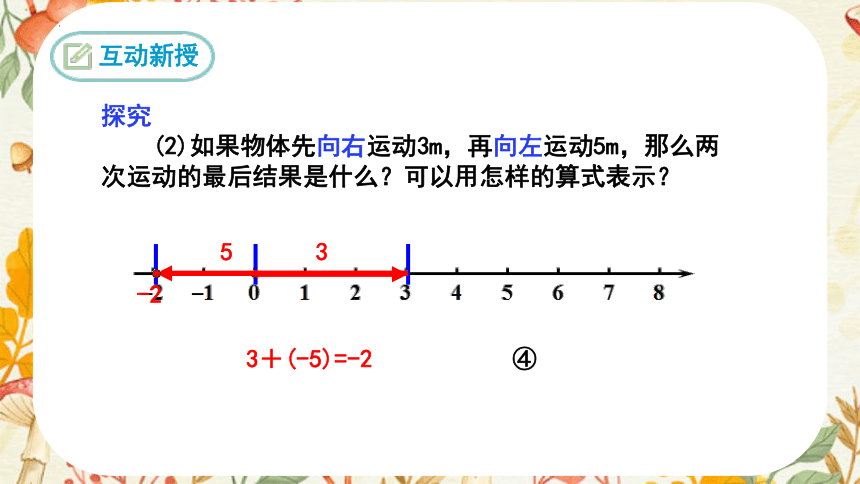
探究
(2)如果物体先向右运动3m,再向左运动5m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
3
5
-2
3+(-5)=-2 ④
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
解:每个队的进球数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球数为
(+2)+(-4)=-(4-2)
=______;
-2
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
解:
互动新授
(-3)+5=2 ③
3+(-5)=-2 ④
从算式③④中,你发现了什么呢?
算式③④都是异号相加.
那你能概括出运算规律吗?
符号相反的两个数相加,结果的符号与绝对值较大的加数的符号相同,并用较大的绝对值减去较小的绝对值.
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
蓝队共进____球,失_____球,净胜球数 _______=________
1
1
1+(-1)
0
解:
例4
已知:如图所示
0
c
b
a
则:
1)a+b 0
2)a+c 0
3)b+c 0
4)利用|a|和|b|表示a+b = 。
5)利用|b|和|c|表示b+c = 。
互动新授
探究
如果物体先向右运动5m,再向左运动5m,那么两次运动的最后结果是如何?可以用怎样的算式表示?
5
5
0
5+(-5)=0 ⑤
例如:
(-4)+(-5 )
(同号两数相加)
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(-2)+6
(绝对值不相等的
异号两数相加)
=+( )
(取绝对值较大的
加数符号)
=+(6-2)
(用较大的绝对值减去
较小的绝对值)
= 4
一 、接力口答:
1、 (+4)+(-7)
2、 (-8)+(-3)
3、 (-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 (-7)+1
8、 0+(-10)
巩固练习
互动新授
5+(-5)=0 ⑤
从算式⑤中,你发现了什么呢?
算式⑤中,两个数互为相反数相加.
那你能概括出运算规律吗?
互为相反数的两个数相加,结果为0.
(1) 0+79
(2) 0+(-12)
(3) 5+0
(4) (-3)+0
练一练
= 5
= 79
= -12
= -3
有理数的加法法则
1.同号两数相加,取相同的符号,并把
绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
巩固练习:
1.如果两个数的和是负数,那么一定是( )
A.这两个数都是负数。
B.两个加数中,一个为负数,一个为零。
C.一个加数为正数,另一个为负数,并
且负数的绝对值大于正数的绝对值。
D.有A.B.C三种可能。
2.如果两个有理数的和为正数,则下列正确的
是( )
A.两个数一定都是正数。
B.两数都不为零。
C.两个数中至少有一个为正数。
D.两个数中至少有一个为负数。
D
C
3、计算:
1、180+(-10)
2、(-10)+(-1)
3、45+(-45)
4、(-23)+0
5、(-25)+0
6、(-13)+5
7、(-1/2)+(+1/3)
8、2/3 +(-3/5)
9、(-0.9)+1.5
10、2.7+(-3.5)
=170
=-11
=0
=-23
=-25
=-8
=-1/6
=1/15
=0.6
=-0.8
4.有理数a、b在数轴上的位置如图所示, 则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
【解析】选A.由有理数a、b在数轴上的位置可知a<0,b>0, ︱a︱<︱b︱,所以a+b>0.
-1
a
0
1
b
记得要多练习呦!
作业设计:p18第2题
人教版七年级数学上册
1.3.1 有理数的加法
(一)
学习目标
1.掌握有理数加法的运算律.
2. 灵活运用运算律进行有理数的加法运算.
3.会用有理数的加法解决实际问题.
(二)
自学检测
计算:
(1)(–83)+(+26)+(–17)+(–26)+(+15).
(2)
(3)
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为
用字母表示为
探究一:
加法运算律
3
﹢
–5
﹦
__
–2
–5
3
﹢
﹦
__
–2
13
﹢
–9
﹦
__
4
–9
13
﹢
﹦
__
4
(2)
(1)
小学学的加法交换律在有理数的加法中还适用吗?
5+3=8
①
(-5)+(-3)=-8
②
互动新授
从算式①②中,你发现了什么呢?
算式①②都是同号相加.
那你能概括出运算规律吗?
符号相同的两个数相加,结果的符号不变,绝对值相加.
互动新授
探究
(1)如果物体先向左运动3m,再向右运动5m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
5
2
(-3)+5=2 ③
有
法
的
理
数
加
例 2
已知|a|=2,|b|=3,求a+b的值.
∵|a|=2,|b|=3,∴a=±2,b=±3
∴当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5
解:
互动新授
探究
(2)如果物体先向右运动3m,再向左运动5m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
3
5
-2
3+(-5)=-2 ④
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
解:每个队的进球数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球数为
(+2)+(-4)=-(4-2)
=______;
-2
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
解:
互动新授
(-3)+5=2 ③
3+(-5)=-2 ④
从算式③④中,你发现了什么呢?
算式③④都是异号相加.
那你能概括出运算规律吗?
符号相反的两个数相加,结果的符号与绝对值较大的加数的符号相同,并用较大的绝对值减去较小的绝对值.
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
蓝队共进____球,失_____球,净胜球数 _______=________
1
1
1+(-1)
0
解:
例4
已知:如图所示
0
c
b
a
则:
1)a+b 0
2)a+c 0
3)b+c 0
4)利用|a|和|b|表示a+b = 。
5)利用|b|和|c|表示b+c = 。
互动新授
探究
如果物体先向右运动5m,再向左运动5m,那么两次运动的最后结果是如何?可以用怎样的算式表示?
5
5
0
5+(-5)=0 ⑤
例如:
(-4)+(-5 )
(同号两数相加)
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(-2)+6
(绝对值不相等的
异号两数相加)
=+( )
(取绝对值较大的
加数符号)
=+(6-2)
(用较大的绝对值减去
较小的绝对值)
= 4
一 、接力口答:
1、 (+4)+(-7)
2、 (-8)+(-3)
3、 (-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 (-7)+1
8、 0+(-10)
巩固练习
互动新授
5+(-5)=0 ⑤
从算式⑤中,你发现了什么呢?
算式⑤中,两个数互为相反数相加.
那你能概括出运算规律吗?
互为相反数的两个数相加,结果为0.
(1) 0+79
(2) 0+(-12)
(3) 5+0
(4) (-3)+0
练一练
= 5
= 79
= -12
= -3
有理数的加法法则
1.同号两数相加,取相同的符号,并把
绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
巩固练习:
1.如果两个数的和是负数,那么一定是( )
A.这两个数都是负数。
B.两个加数中,一个为负数,一个为零。
C.一个加数为正数,另一个为负数,并
且负数的绝对值大于正数的绝对值。
D.有A.B.C三种可能。
2.如果两个有理数的和为正数,则下列正确的
是( )
A.两个数一定都是正数。
B.两数都不为零。
C.两个数中至少有一个为正数。
D.两个数中至少有一个为负数。
D
C
3、计算:
1、180+(-10)
2、(-10)+(-1)
3、45+(-45)
4、(-23)+0
5、(-25)+0
6、(-13)+5
7、(-1/2)+(+1/3)
8、2/3 +(-3/5)
9、(-0.9)+1.5
10、2.7+(-3.5)
=170
=-11
=0
=-23
=-25
=-8
=-1/6
=1/15
=0.6
=-0.8
4.有理数a、b在数轴上的位置如图所示, 则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
【解析】选A.由有理数a、b在数轴上的位置可知a<0,b>0, ︱a︱<︱b︱,所以a+b>0.
-1
a
0
1
b
记得要多练习呦!
作业设计:p18第2题
