1.3 正方形的性质与判定 第1课时 课件(共23张PPT) 北师大版九年级上册数学
文档属性
| 名称 | 1.3 正方形的性质与判定 第1课时 课件(共23张PPT) 北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 831.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 21:21:12 | ||
图片预览








文档简介
(共23张PPT)
第一章 特殊平行四边形
3 正方形的性质与判定 第1课时
1.知道正方形的概念、性质;知道正方形是轴对称图形.
2.知道正方形与平行四边形、菱形、矩形的区别与联系.
3.通过四边形的从属关系渗透集合思想,明晰这几种特殊的平行四边形的从属关系.
◎重点:正方形的性质,正方形与菱形、矩形的关系.
师:从平行四边形出发,添加一个条件就得到了特殊的平行四边形,即矩形或者菱形.你能否模仿这个方法,从学过的图形出发,添加一个或者几个条件,得到正方形?
生:平行四边形添加两个条件,一个角是直角,一组邻边相等,可以得到正方形.
师:请具体说明.
生:起始图形是平行四边形,添加一个角是直角这个条件,由于平行的性质,得到了四个角都是直角;再添加一组邻边相等,由于平行四边形对边相等,就得到了四边相等.四个角是直角,四边相等的图形就是正方形了.
师:说得真好!于是我们得到了正方形的定义,即有一组邻边相等并且有一个角是直角的平行四边形叫做正方形(板书),这个定义是正方形的判定方法之一.今天我们就一起来探究正方形.
正方形
阅读教材本课时相关内容,完成下列问题.
1.正方形的定义:有一组邻边 相等 ,并且有一个角是直角的平行四边形叫做正方形.
相等
2.正方形的性质:正方形的四个角都是 直角 ,四条边都 相等 .正方形的两条对角线 相等并且互相垂直平分 .正方形的对角线 平分 每一组对角.正方形是 轴对称 图形,它有 四 条对称轴.
直角
相等
相等并且互相垂直平分
平分
轴对称
四
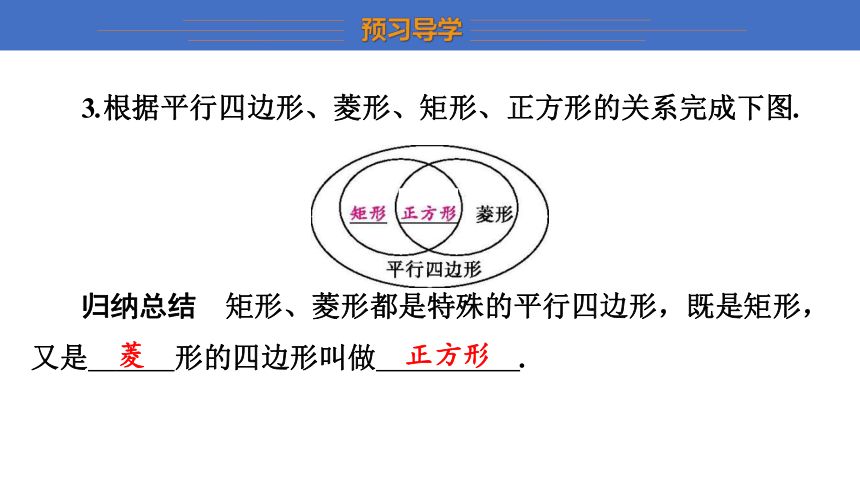
3.根据平行四边形、菱形、矩形、正方形的关系完成下图.
归纳总结 矩形、菱形都是特殊的平行四边形,既是矩形,又是 菱 形的四边形叫做 正方形 .
菱
正方形
利用自制教具或借助几何画板等现代教学手段演示矩形到正方形,菱形到正方形的变化过程,帮助学生理解正方形与菱形、矩形的联系与区别.
·导学建议·
1.正方形具备而菱形不具备的性质是( C )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
C
2.如图,E是正方形ABCD的边AB延长线上一点,且BD=BE,则∠BED的大小为( A )
A.22.5° B.15° C.30° D.45°
3.正方形的一条边长是3,那么它的对角线长是 3 ,面积是 9 .
A
3
9
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有( B )
A.4个 B.3个 C.2个 D.1个
B
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC.
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
解:(1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°.
又∵EC=EC,∴△BEC≌△DEC(SAS).
(2)∵△BEC≌△DEC,∴∠BEC=∠DEC=∠BED. ∵∠BED=120°,∴∠BEC=60°=∠AEF,∴∠EFD=60°+45°=105°.
如图,在正方形ABCD中,AC、BD交于点O,点E在OA上,点G在OB上,且OE=OG,CG的延长线交BE于点F,猜想并证明CG和EB的大小及位置关系.
证明:∵四边形ABCD是正方形,∴OC=OB,∠COG=∠BOE=90°.∵OE=OG,∴△BOE≌△COG(SAS),∴CG=BE,∠CEF=∠CGO,∵∠GCO+∠CGO=90°,∴∠GCO+∠CEF=90°,∴∠CFE=90°,∴CF⊥BE.
解:CG⊥BE,CG=BE.
如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.(1)试探索BE和CF的关系,并说明理由;(2)你能找到哪两个图形可以通过旋转而相互得到?并指出旋转中心和旋转角.
解:(1)BE=CF,BE⊥CF.理由:在正方形ACDE和正方形ABGF中,
∵AF=AB,AC=AE,∠FAB=∠EAC=90°,
∴∠FAC=∠BAE,∴△AFC≌△ABE(SAS),BE=CF,∠AEB=∠ACF.∵∠EHC+∠HED+∠D+∠DCH=360°,∠AED=∠AEB+∠HED=90°,∠D=∠ACD=90°,
∴∠EHC=90°.
(2)△ABE和△AFC可以通过旋转而相互得到,旋转中心是点A,旋转角为90°.
方法归纳交流
两条线段间的关系探索类问题,一般从线段的位置关系和数量关系两个方面去探究.
如图,在正方形ABCD中,AC,BD相交于点O,E,F分别在OA,OD上,∠ABE=∠DCF.
(1)求证:△ABE≌△DCF.
(2)若BC=4,AE=3,求BE的长.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAE=∠CDF=45°.
∵∠ABE=∠DCF,
在△ABE与△DCF中,
∴△ABE≌△DCF(ASA).
(2)∵四边形ABCD是正方形,
∴AB=BC,OA=OB=OC=OD,∠ABC=∠AOB=90°.
∵BC=4,
∴AB=4.
∴AC===8,
∴OA=OB=4.
∵AE=3,
∴OE=OA-AE=4-3=1,
在Rt△BOE中,BE===.
故BE的长为.
第一章 特殊平行四边形
3 正方形的性质与判定 第1课时
1.知道正方形的概念、性质;知道正方形是轴对称图形.
2.知道正方形与平行四边形、菱形、矩形的区别与联系.
3.通过四边形的从属关系渗透集合思想,明晰这几种特殊的平行四边形的从属关系.
◎重点:正方形的性质,正方形与菱形、矩形的关系.
师:从平行四边形出发,添加一个条件就得到了特殊的平行四边形,即矩形或者菱形.你能否模仿这个方法,从学过的图形出发,添加一个或者几个条件,得到正方形?
生:平行四边形添加两个条件,一个角是直角,一组邻边相等,可以得到正方形.
师:请具体说明.
生:起始图形是平行四边形,添加一个角是直角这个条件,由于平行的性质,得到了四个角都是直角;再添加一组邻边相等,由于平行四边形对边相等,就得到了四边相等.四个角是直角,四边相等的图形就是正方形了.
师:说得真好!于是我们得到了正方形的定义,即有一组邻边相等并且有一个角是直角的平行四边形叫做正方形(板书),这个定义是正方形的判定方法之一.今天我们就一起来探究正方形.
正方形
阅读教材本课时相关内容,完成下列问题.
1.正方形的定义:有一组邻边 相等 ,并且有一个角是直角的平行四边形叫做正方形.
相等
2.正方形的性质:正方形的四个角都是 直角 ,四条边都 相等 .正方形的两条对角线 相等并且互相垂直平分 .正方形的对角线 平分 每一组对角.正方形是 轴对称 图形,它有 四 条对称轴.
直角
相等
相等并且互相垂直平分
平分
轴对称
四
3.根据平行四边形、菱形、矩形、正方形的关系完成下图.
归纳总结 矩形、菱形都是特殊的平行四边形,既是矩形,又是 菱 形的四边形叫做 正方形 .
菱
正方形
利用自制教具或借助几何画板等现代教学手段演示矩形到正方形,菱形到正方形的变化过程,帮助学生理解正方形与菱形、矩形的联系与区别.
·导学建议·
1.正方形具备而菱形不具备的性质是( C )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
C
2.如图,E是正方形ABCD的边AB延长线上一点,且BD=BE,则∠BED的大小为( A )
A.22.5° B.15° C.30° D.45°
3.正方形的一条边长是3,那么它的对角线长是 3 ,面积是 9 .
A
3
9
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有( B )
A.4个 B.3个 C.2个 D.1个
B
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC.
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
解:(1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°.
又∵EC=EC,∴△BEC≌△DEC(SAS).
(2)∵△BEC≌△DEC,∴∠BEC=∠DEC=∠BED. ∵∠BED=120°,∴∠BEC=60°=∠AEF,∴∠EFD=60°+45°=105°.
如图,在正方形ABCD中,AC、BD交于点O,点E在OA上,点G在OB上,且OE=OG,CG的延长线交BE于点F,猜想并证明CG和EB的大小及位置关系.
证明:∵四边形ABCD是正方形,∴OC=OB,∠COG=∠BOE=90°.∵OE=OG,∴△BOE≌△COG(SAS),∴CG=BE,∠CEF=∠CGO,∵∠GCO+∠CGO=90°,∴∠GCO+∠CEF=90°,∴∠CFE=90°,∴CF⊥BE.
解:CG⊥BE,CG=BE.
如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.(1)试探索BE和CF的关系,并说明理由;(2)你能找到哪两个图形可以通过旋转而相互得到?并指出旋转中心和旋转角.
解:(1)BE=CF,BE⊥CF.理由:在正方形ACDE和正方形ABGF中,
∵AF=AB,AC=AE,∠FAB=∠EAC=90°,
∴∠FAC=∠BAE,∴△AFC≌△ABE(SAS),BE=CF,∠AEB=∠ACF.∵∠EHC+∠HED+∠D+∠DCH=360°,∠AED=∠AEB+∠HED=90°,∠D=∠ACD=90°,
∴∠EHC=90°.
(2)△ABE和△AFC可以通过旋转而相互得到,旋转中心是点A,旋转角为90°.
方法归纳交流
两条线段间的关系探索类问题,一般从线段的位置关系和数量关系两个方面去探究.
如图,在正方形ABCD中,AC,BD相交于点O,E,F分别在OA,OD上,∠ABE=∠DCF.
(1)求证:△ABE≌△DCF.
(2)若BC=4,AE=3,求BE的长.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAE=∠CDF=45°.
∵∠ABE=∠DCF,
在△ABE与△DCF中,
∴△ABE≌△DCF(ASA).
(2)∵四边形ABCD是正方形,
∴AB=BC,OA=OB=OC=OD,∠ABC=∠AOB=90°.
∵BC=4,
∴AB=4.
∴AC===8,
∴OA=OB=4.
∵AE=3,
∴OE=OA-AE=4-3=1,
在Rt△BOE中,BE===.
故BE的长为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
