1.2 矩形的性质与判定 第2课时课件(共17张PPT) 北师大版九年级上册数学
文档属性
| 名称 | 1.2 矩形的性质与判定 第2课时课件(共17张PPT) 北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 863.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
2 矩形的性质与判定 第2课时
第一章 特殊平行四边形
1.知道矩形的判定条件与方法.
2.能运用矩形的判定定理与方法进行合理推理证明.
◎重点:矩形的判定方法,矩形判定定理的应用.
活动导入
模拟展示工人师傅做铝合金窗框的检测过程.
背景介绍:工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD,EF=GH;
(2)摆放成四边形(如图2);
(3)将直角尺靠紧窗框的一个角(如图3),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格.
你能说明其中的道理吗?
操作活动:学生画矩形.
问题:大家平时是如何画矩形的呢?请利用手中的三尺或圆规在白纸上画出一个矩形.
1.你的矩形是如何画出来的?(学生交流各自画法)
2.你画出的四边形一定是矩形吗?说明理由.
矩形的判定定理
阅读教材本课时相关内容,完成下列问题.
1.对角线 相等 的平行四边形是矩形;
2.有一个角是 直角 的平行四边形是矩形;
3.有三个角是 直角 的四边形是矩形;
4.对角线 对角线相等 的四边形是矩形.
相等
直角
直角
相等且互相平分
·导学建议·
1.本节课的引入也可让学生回忆矩形的性质,然后让学生说出相应的逆命题,再判断逆命题的真假,从而引出判定定理.
2.利用自制教具或借助几何画板等现代教学手段演示平行四边形到矩形的变化过程,加深学生对矩形判别的理解.
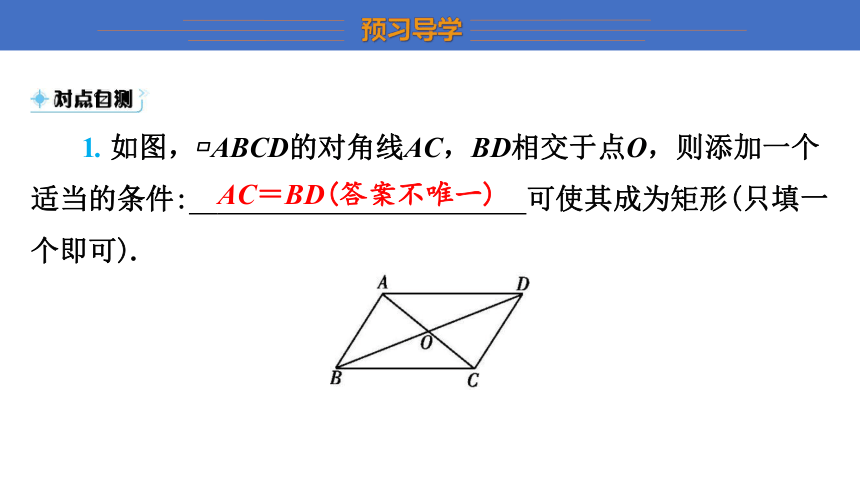
1. 如图, ABCD的对角线AC,BD相交于点O,则添加一个适当的条件: AC=BD(答案不唯一) 可使其成为矩形(只填一个即可).
AC=BD(答案不唯一)
2. 如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为 60 度时,四边形ABFE为矩形.
60
如图,四边形ABCD的对角线AC、BD相等,则下列条件能判定四边形ABCD为矩形的是( B )
A.BA=BC B.AC、BD互相平分
C.AC⊥BD D.AB∥CD
方法归纳交流 对角线互相平分且相等的四边形是矩形.
B
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
证明:(1)∵BE=CF,BF=BE+EF,CE=CF+EF,∴BF=CE.∵四边形ABCD是平行四边形,∴AB=DC.又∵AF=DE,∴△ABF≌△DCE(SSS).
(2)∵△ABF≌△DCE,∴∠B=∠C.∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠C=180°,∴∠B=∠C=90°,∴四边形ABCD是矩形.
如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF.
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
解:(1)证明:由平行四边形ABCD,得到AB∥CD,则∠ABE=∠FCE,又EB=EC,∠AEB=∠FEC,
∴△ABE≌△FCE(ASA),∴AB=CF.
(2)当BC=AF时,四边形ABFC是矩形.由△ABE≌△FCE,得到EA=EF,EB=EC,∴四边形ABFC是平行四边形,又∵BC=AF,∴四边形ABFC是矩形.
方法归纳交流
条件探索类的问题,一般是把结论当作题设,反向推导出与问题相关的结论.
如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数.
(2)求证:四边形FDEC是矩形.
解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°.
(2)证明:∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,∠ACB=90°,
∴四边形DECF是矩形.
2 矩形的性质与判定 第2课时
第一章 特殊平行四边形
1.知道矩形的判定条件与方法.
2.能运用矩形的判定定理与方法进行合理推理证明.
◎重点:矩形的判定方法,矩形判定定理的应用.
活动导入
模拟展示工人师傅做铝合金窗框的检测过程.
背景介绍:工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD,EF=GH;
(2)摆放成四边形(如图2);
(3)将直角尺靠紧窗框的一个角(如图3),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格.
你能说明其中的道理吗?
操作活动:学生画矩形.
问题:大家平时是如何画矩形的呢?请利用手中的三尺或圆规在白纸上画出一个矩形.
1.你的矩形是如何画出来的?(学生交流各自画法)
2.你画出的四边形一定是矩形吗?说明理由.
矩形的判定定理
阅读教材本课时相关内容,完成下列问题.
1.对角线 相等 的平行四边形是矩形;
2.有一个角是 直角 的平行四边形是矩形;
3.有三个角是 直角 的四边形是矩形;
4.对角线 对角线相等 的四边形是矩形.
相等
直角
直角
相等且互相平分
·导学建议·
1.本节课的引入也可让学生回忆矩形的性质,然后让学生说出相应的逆命题,再判断逆命题的真假,从而引出判定定理.
2.利用自制教具或借助几何画板等现代教学手段演示平行四边形到矩形的变化过程,加深学生对矩形判别的理解.
1. 如图, ABCD的对角线AC,BD相交于点O,则添加一个适当的条件: AC=BD(答案不唯一) 可使其成为矩形(只填一个即可).
AC=BD(答案不唯一)
2. 如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为 60 度时,四边形ABFE为矩形.
60
如图,四边形ABCD的对角线AC、BD相等,则下列条件能判定四边形ABCD为矩形的是( B )
A.BA=BC B.AC、BD互相平分
C.AC⊥BD D.AB∥CD
方法归纳交流 对角线互相平分且相等的四边形是矩形.
B
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
证明:(1)∵BE=CF,BF=BE+EF,CE=CF+EF,∴BF=CE.∵四边形ABCD是平行四边形,∴AB=DC.又∵AF=DE,∴△ABF≌△DCE(SSS).
(2)∵△ABF≌△DCE,∴∠B=∠C.∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠C=180°,∴∠B=∠C=90°,∴四边形ABCD是矩形.
如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF.
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
解:(1)证明:由平行四边形ABCD,得到AB∥CD,则∠ABE=∠FCE,又EB=EC,∠AEB=∠FEC,
∴△ABE≌△FCE(ASA),∴AB=CF.
(2)当BC=AF时,四边形ABFC是矩形.由△ABE≌△FCE,得到EA=EF,EB=EC,∴四边形ABFC是平行四边形,又∵BC=AF,∴四边形ABFC是矩形.
方法归纳交流
条件探索类的问题,一般是把结论当作题设,反向推导出与问题相关的结论.
如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数.
(2)求证:四边形FDEC是矩形.
解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°.
(2)证明:∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,∠ACB=90°,
∴四边形DECF是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
