4.3.1 角与角的大小比较 课件(共20张PPT) 湘教版七年级数学上册
文档属性
| 名称 | 4.3.1 角与角的大小比较 课件(共20张PPT) 湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1024.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第四章 图形的认识
4.3.1 角与角的大小比较
1.理解角的概念,能用符号表示一个角
2.知道角平分线的概念
3.掌握比较角大小的方法,并会进行比较
钟面上的时针与分针、圆规的两只脚之间、折扇的扇骨与扇骨之间都给我们以什么样的形象?
将射线OA绕点O旋转到OB位置时,就出现了角的形象,因此,我们把一条射线绕着它的端点从一个位置旋转到另一个位置时,所成的图形叫做角.
射线的端点O叫做角的顶点.
射线原来的位置OA叫做角的始边,旋转后的位置OB叫做角的终边,
O
A
B
始边
终边
角的内部
从始边旋转到终边所扫过的区域,叫做角的内部.
角的始边和终边统称为角的边,
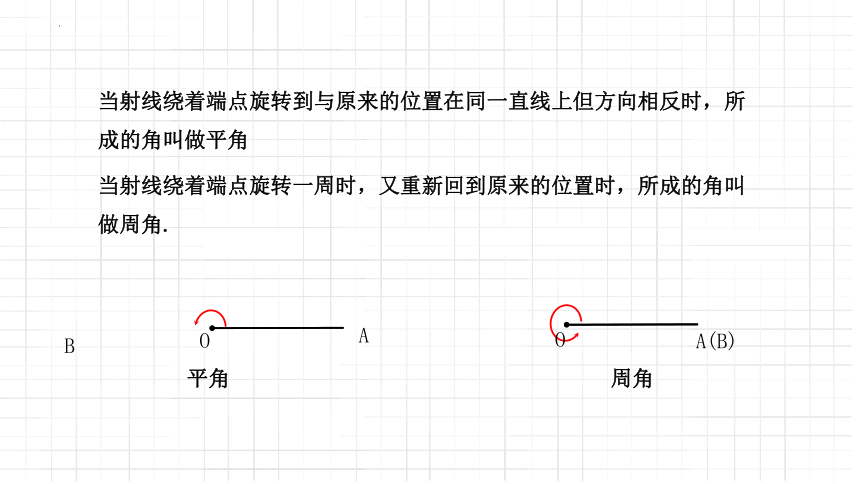
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角
O
A
B
当射线绕着端点旋转一周时,又重新回到原来的位置时,所成的角叫做周角.
A
O
(B)
平角
周角
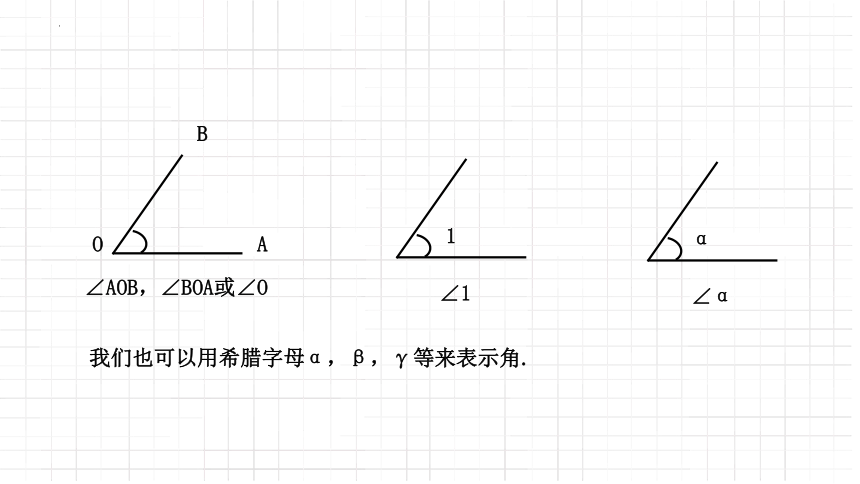
我们也可以用希腊字母α,β,γ等来表示角.
B
O
A
∠AOB,∠BOA或∠O
1
∠1
α
∠α
想一想
类比线段长短的比较方法,怎么比较图中的∠ABC和∠DEF的大小?
A
B
C
D
E
F
1.测量法
∠ABC >∠DEF
B
C
A
F
E
D
70°
30°
量角器量角要注意:①对中;②重合;③读数
B
C
A
E
D
F
2.叠合法
DE边在∠ABC的内部,则∠ABC > ∠DEF
E
D
F
B
A
C
E
D
F
B
A
C
E
D
F
B
A
C
ED与BA重合,那么∠ABC___∠DEF.
ED落在∠ABC内部,∠ABC___∠DEF.
=
>
<
ED落在∠ABC外部,∠ABC___∠DEF.
归纳总结
通常角的大小比较方法有两种:
(1)是把两个角的顶点重合,一条边重合,则在重合边同旁的另一边在外面的角大于在里面的角,这称为叠合法;
(2)是用量角器量出两个角的度数,这称为测量法.
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
几何语言
O
B
A
C
因为0C是∠AOB的角平分线
或∠AOB=2∠B0C=2∠AOC
所以∠A0C=∠B0C= ∠AOB
例1:如右图:
(1)写出能用一个字母表示的角;
解:∠A,∠C;
分析:本题目主要考查角的表示方法,从角的顶点去思考有几个角是解决此题的关键.
(2)写出以B为顶点的角;
解:∠ABE,∠ABC,∠EBC;
(3)图中共有几个小于平角的角
解:共有7个小于平角的角,
分别是:
以A为顶点的是∠A,
以B为顶点的是∠ABE、∠ABC、∠EBC,
以C为顶点的是∠C,
以E为顶点的是∠AEB、∠CEB.
注意:角的表示方法要恰当选取,特别是在同一顶点处不止一个角时,注意正确表示.
1.图中,角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
C
A
B
∠ABC
C
B
A
∠ABC
B
A
直线是平角
O
A
直线是平角
B
当用三个字母表示一个角时,中间的字母必须是角的顶点
2.如图,下列说法正确的是( )
A.∠BAC和∠DAE是不同的两个角
B.∠ABC和∠ACB是同一个角
C.∠ADE就是∠D
D.∠ABC可以用∠B表示
D
用一个大写字母表示一个角时,前提条件是以该点为顶点的角只有一个,否则不能用这种方法表示角
角的两边张开越大,角就越大
例2.如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
O
B
F
D
E
A
C
解:∵OD在∠FOE的内部,
∴∠FOD<∠FOE.
(2)借助量角器比较∠AOE与∠DOF的大小.
∠AOE=20°
∠DOF=40°
∴∠AOE<∠DOF
3. 如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,试比较下列各角的大小.
(1)∠AOB ∠BOD;
(2)∠AOE ∠AOB;
(3)∠BOD ∠FOB;
(4)∠AOB ∠FOB;
(5)∠DOE ∠BOD.
>
>
<
=
>
4.如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A
O
A
B
C
D
A.∠COD = ∠AOC B.∠AOD = ∠AOB
C.∠BOD = ∠AOB D.∠BOC = ∠AOB
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
第四章 图形的认识
4.3.1 角与角的大小比较
1.理解角的概念,能用符号表示一个角
2.知道角平分线的概念
3.掌握比较角大小的方法,并会进行比较
钟面上的时针与分针、圆规的两只脚之间、折扇的扇骨与扇骨之间都给我们以什么样的形象?
将射线OA绕点O旋转到OB位置时,就出现了角的形象,因此,我们把一条射线绕着它的端点从一个位置旋转到另一个位置时,所成的图形叫做角.
射线的端点O叫做角的顶点.
射线原来的位置OA叫做角的始边,旋转后的位置OB叫做角的终边,
O
A
B
始边
终边
角的内部
从始边旋转到终边所扫过的区域,叫做角的内部.
角的始边和终边统称为角的边,
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角
O
A
B
当射线绕着端点旋转一周时,又重新回到原来的位置时,所成的角叫做周角.
A
O
(B)
平角
周角
我们也可以用希腊字母α,β,γ等来表示角.
B
O
A
∠AOB,∠BOA或∠O
1
∠1
α
∠α
想一想
类比线段长短的比较方法,怎么比较图中的∠ABC和∠DEF的大小?
A
B
C
D
E
F
1.测量法
∠ABC >∠DEF
B
C
A
F
E
D
70°
30°
量角器量角要注意:①对中;②重合;③读数
B
C
A
E
D
F
2.叠合法
DE边在∠ABC的内部,则∠ABC > ∠DEF
E
D
F
B
A
C
E
D
F
B
A
C
E
D
F
B
A
C
ED与BA重合,那么∠ABC___∠DEF.
ED落在∠ABC内部,∠ABC___∠DEF.
=
>
<
ED落在∠ABC外部,∠ABC___∠DEF.
归纳总结
通常角的大小比较方法有两种:
(1)是把两个角的顶点重合,一条边重合,则在重合边同旁的另一边在外面的角大于在里面的角,这称为叠合法;
(2)是用量角器量出两个角的度数,这称为测量法.
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
几何语言
O
B
A
C
因为0C是∠AOB的角平分线
或∠AOB=2∠B0C=2∠AOC
所以∠A0C=∠B0C= ∠AOB
例1:如右图:
(1)写出能用一个字母表示的角;
解:∠A,∠C;
分析:本题目主要考查角的表示方法,从角的顶点去思考有几个角是解决此题的关键.
(2)写出以B为顶点的角;
解:∠ABE,∠ABC,∠EBC;
(3)图中共有几个小于平角的角
解:共有7个小于平角的角,
分别是:
以A为顶点的是∠A,
以B为顶点的是∠ABE、∠ABC、∠EBC,
以C为顶点的是∠C,
以E为顶点的是∠AEB、∠CEB.
注意:角的表示方法要恰当选取,特别是在同一顶点处不止一个角时,注意正确表示.
1.图中,角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
C
A
B
∠ABC
C
B
A
∠ABC
B
A
直线是平角
O
A
直线是平角
B
当用三个字母表示一个角时,中间的字母必须是角的顶点
2.如图,下列说法正确的是( )
A.∠BAC和∠DAE是不同的两个角
B.∠ABC和∠ACB是同一个角
C.∠ADE就是∠D
D.∠ABC可以用∠B表示
D
用一个大写字母表示一个角时,前提条件是以该点为顶点的角只有一个,否则不能用这种方法表示角
角的两边张开越大,角就越大
例2.如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
O
B
F
D
E
A
C
解:∵OD在∠FOE的内部,
∴∠FOD<∠FOE.
(2)借助量角器比较∠AOE与∠DOF的大小.
∠AOE=20°
∠DOF=40°
∴∠AOE<∠DOF
3. 如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,试比较下列各角的大小.
(1)∠AOB ∠BOD;
(2)∠AOE ∠AOB;
(3)∠BOD ∠FOB;
(4)∠AOB ∠FOB;
(5)∠DOE ∠BOD.
>
>
<
=
>
4.如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A
O
A
B
C
D
A.∠COD = ∠AOC B.∠AOD = ∠AOB
C.∠BOD = ∠AOB D.∠BOC = ∠AOB
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
同课章节目录
