4.2.2 线段的应用和作图 课件(共19张PPT) 湘教版七年级数学上册
文档属性
| 名称 | 4.2.2 线段的应用和作图 课件(共19张PPT) 湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 562.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第4章 图形的认识
4.2.2 线段的应用和作图
1.掌握比较线段长短的方法.
2.会用直尺和圆规作两条线段的和与差,
3.知道“两点之间的所有连线中,线段最短”的基本事实,
4.理解线段中点的概念,并会用其解决问题.
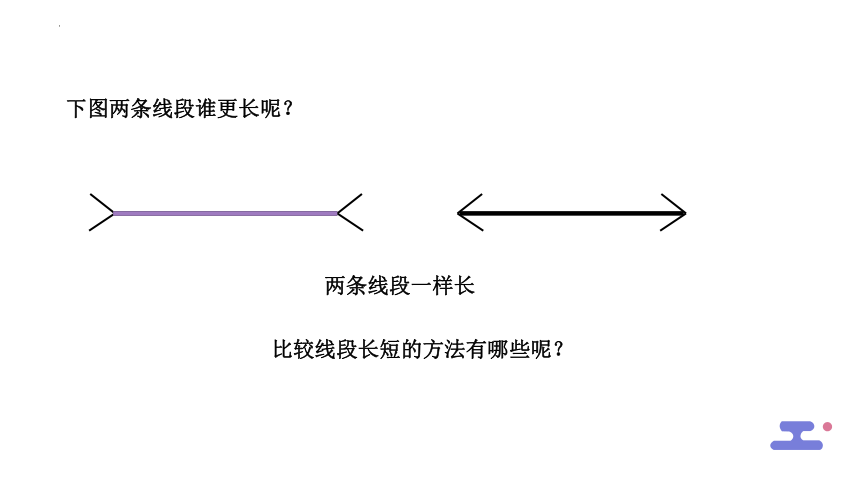
下图两条线段谁更长呢?
两条线段一样长
比较线段长短的方法有哪些呢?
已知线段AB、CD,为了便于表示, 我们把线段 AB的长度记做AB.尝试比较AB、CD的长短.
A
B
C
D
方法一:测量法——借助刻度尺.
用刻度尺分别量出AB、CD的长度,
长度大的线段较长;长度小的线段较短;
当长度相等时,两条线段相等;
方法二:叠合法
将线段AB放到线段CD上,使点A和点C重合,点B和点D在点A(点C)的同侧.
A
B
C
D
(1)如下图,如果点B和点D重合,就说明线段AB与CD相等,记作AB=CD.
A
B
C
D
(2)如下图,如果点B在线段CD上,就说线段AB小于CD,记作ABA
B
C
D
(3)如下图,如果点B在线段CD外,就说线段AB大于CD,记作AB>CD.
A
B
C
D
如图,点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,
线段BC就是b与a的差 ,记做c=b- a .
A
C
B
设AB=a,AC=b, BC=c,则线段AC就是线段a与线段c的和,记做b =a+c ;
邮局
学校
商店
小丽家
我要到学校可以怎么走呀?哪一条路最近呀?
小丽
红色的路线为最短路线.
想一想
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
连接两点的线段的长度,叫做这两点间的距离.
例1. 如图,已知线段a,借助圆规和直尺作一条线段等于已知线段等于2a.
(1)作射线AD;
(2)用圆规在射线AD上顺次截取AB=BC=a.
(3)线段AC为所求作的线段.
A D
B
a
解:作图步骤如下:
这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
C
例2.如图,已知线段a,b(a > b ), 作一条线段使它等于a-b.
b
a
(1)作射线AF;
(2)用圆规在射线AF上截取AC=a.
(4)线段BC为所求作的线段.
A F
C
解:作图步骤如下:
B
(3)在射线AC上截取AB=b.
尺规作图的应用注意事项:
1.先画一条射线;
2.按作图要求用圆规截长 ;
4.不可以使用刻度尺度量 .
5.作出结论(∴线段即为所求) .
3.以射线的端点为圆心,圆规所截长度为半径作弧 ;
归纳总结
D
1.下列说法正确的个数为( )
①线段的长度比较可以由刻度尺测量;
②比较线段长度时,在同一条直线上,把一端点重合,再比较另一端点是否重合;
③线段的长度实质是两点间的距离;
④连结两点间的所有连线中,线段最短.
A.1 B.2 C.3 D.4
2. 如图,已知线段a,b,画一条线段AB,使AB=2a-b.
a
b
A
B
2a-b
2a
b
解:如图所示:
A
B
C
B 是线段 AC 的中点
几何语言: ∵ B 是线段 AC 的中点
∴ AB = BC = AC ( 或 AC = 2 AB = 2 BC )
反之也成立:∵ AB = BC = AC ( 或 AC = 2 AB = 2 BC )
∴ B 是线段 AC 的中点
若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
例3.如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
因为点O是线段AC的中点,
所以OB=OC-BC=3.5-3=0.5 cm.
所以OC= AC=3.5 cm.
所以AC=AB+ BC=7 cm.
4.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
解:(1)因为点M是线段AC的中点,点N是线段BC的中点;
所以2NC=BC=AB-AC=8cm,故NC=4cm.
所以BC=2NC,AC=2AM=12cm,
4.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(2)如果MN=6 cm,求AB的长.
(2)因为点M是线段AC的中点,点N是线段BC的中点;
所以AB=AC+BC=2CM+2CN=2(CM+CN)=2MN=12cm
所以BC=2NC,AC=2CM;
3.基本事实:两点之间的所有连线中,线段最短
4.线段的中点:若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
连接两点的线段的长度,叫做这两点间的距离
1.比较两条线段长短的方法:度量法、叠合法
2.尺规作图:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.
第4章 图形的认识
4.2.2 线段的应用和作图
1.掌握比较线段长短的方法.
2.会用直尺和圆规作两条线段的和与差,
3.知道“两点之间的所有连线中,线段最短”的基本事实,
4.理解线段中点的概念,并会用其解决问题.
下图两条线段谁更长呢?
两条线段一样长
比较线段长短的方法有哪些呢?
已知线段AB、CD,为了便于表示, 我们把线段 AB的长度记做AB.尝试比较AB、CD的长短.
A
B
C
D
方法一:测量法——借助刻度尺.
用刻度尺分别量出AB、CD的长度,
长度大的线段较长;长度小的线段较短;
当长度相等时,两条线段相等;
方法二:叠合法
将线段AB放到线段CD上,使点A和点C重合,点B和点D在点A(点C)的同侧.
A
B
C
D
(1)如下图,如果点B和点D重合,就说明线段AB与CD相等,记作AB=CD.
A
B
C
D
(2)如下图,如果点B在线段CD上,就说线段AB小于CD,记作AB
B
C
D
(3)如下图,如果点B在线段CD外,就说线段AB大于CD,记作AB>CD.
A
B
C
D
如图,点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,
线段BC就是b与a的差 ,记做c=b- a .
A
C
B
设AB=a,AC=b, BC=c,则线段AC就是线段a与线段c的和,记做b =a+c ;
邮局
学校
商店
小丽家
我要到学校可以怎么走呀?哪一条路最近呀?
小丽
红色的路线为最短路线.
想一想
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
连接两点的线段的长度,叫做这两点间的距离.
例1. 如图,已知线段a,借助圆规和直尺作一条线段等于已知线段等于2a.
(1)作射线AD;
(2)用圆规在射线AD上顺次截取AB=BC=a.
(3)线段AC为所求作的线段.
A D
B
a
解:作图步骤如下:
这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
C
例2.如图,已知线段a,b(a > b ), 作一条线段使它等于a-b.
b
a
(1)作射线AF;
(2)用圆规在射线AF上截取AC=a.
(4)线段BC为所求作的线段.
A F
C
解:作图步骤如下:
B
(3)在射线AC上截取AB=b.
尺规作图的应用注意事项:
1.先画一条射线;
2.按作图要求用圆规截长 ;
4.不可以使用刻度尺度量 .
5.作出结论(∴线段即为所求) .
3.以射线的端点为圆心,圆规所截长度为半径作弧 ;
归纳总结
D
1.下列说法正确的个数为( )
①线段的长度比较可以由刻度尺测量;
②比较线段长度时,在同一条直线上,把一端点重合,再比较另一端点是否重合;
③线段的长度实质是两点间的距离;
④连结两点间的所有连线中,线段最短.
A.1 B.2 C.3 D.4
2. 如图,已知线段a,b,画一条线段AB,使AB=2a-b.
a
b
A
B
2a-b
2a
b
解:如图所示:
A
B
C
B 是线段 AC 的中点
几何语言: ∵ B 是线段 AC 的中点
∴ AB = BC = AC ( 或 AC = 2 AB = 2 BC )
反之也成立:∵ AB = BC = AC ( 或 AC = 2 AB = 2 BC )
∴ B 是线段 AC 的中点
若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
例3.如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
因为点O是线段AC的中点,
所以OB=OC-BC=3.5-3=0.5 cm.
所以OC= AC=3.5 cm.
所以AC=AB+ BC=7 cm.
4.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
解:(1)因为点M是线段AC的中点,点N是线段BC的中点;
所以2NC=BC=AB-AC=8cm,故NC=4cm.
所以BC=2NC,AC=2AM=12cm,
4.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(2)如果MN=6 cm,求AB的长.
(2)因为点M是线段AC的中点,点N是线段BC的中点;
所以AB=AC+BC=2CM+2CN=2(CM+CN)=2MN=12cm
所以BC=2NC,AC=2CM;
3.基本事实:两点之间的所有连线中,线段最短
4.线段的中点:若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
连接两点的线段的长度,叫做这两点间的距离
1.比较两条线段长短的方法:度量法、叠合法
2.尺规作图:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.
同课章节目录
