惠州市第一中学2023-2024学年高一上学期10月第一次阶段考试数学试卷(含解析)
文档属性
| 名称 | 惠州市第一中学2023-2024学年高一上学期10月第一次阶段考试数学试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 573.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-22 00:00:00 | ||
图片预览





文档简介
惠州市第一中学2023-2024学年高一上学期10月第一次阶段考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知全集,,则( )
A. B. C. D.
2、设四边形ABCD为矩形,四边形ABCD为平行四边形,p是q的________条件( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、集合,若,则满足条件的集合B的个数为( )
A.4 B.5 C.7 D.8
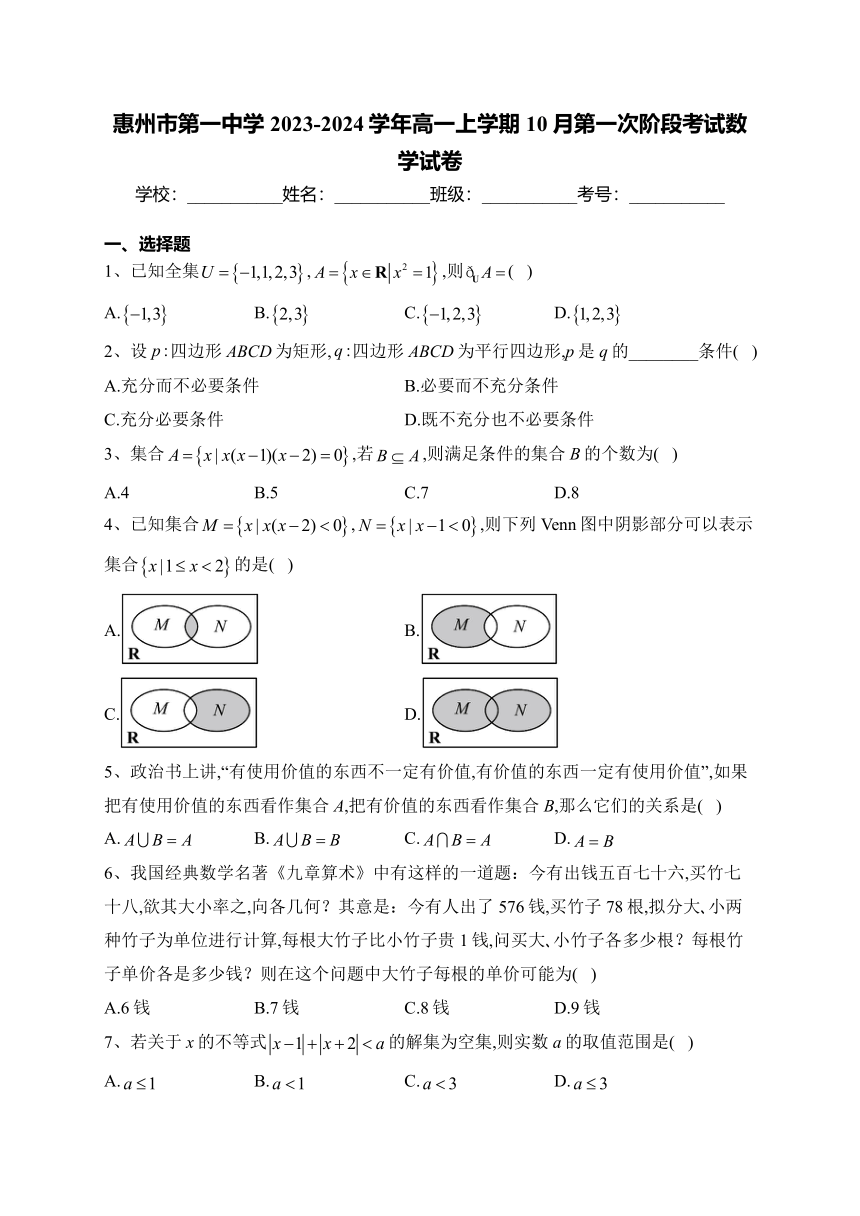
4、已知集合,,则下列Venn图中阴影部分可以表示集合的是( )
A. B.
C. D.
5、政治书上讲,“有使用价值的东西不一定有价值,有价值的东西一定有使用价值”,如果把有使用价值的东西看作集合A,把有价值的东西看作集合B,那么它们的关系是( )
A. B. C. D.
6、我国经典数学名著《九章算术》中有这样的一道题:今有出钱五百七十六,买竹七十八,欲其大小率之,向各几何?其意是:今有人出了576钱,买竹子78根,拟分大 小两种竹子为单位进行计算,每根大竹子比小竹子贵1钱,问买大 小竹子各多少根?每根竹子单价各是多少钱?则在这个问题中大竹子每根的单价可能为( )
A.6钱 B.7钱 C.8钱 D.9钱
7、若关于x的不等式的解集为空集,则实数a的取值范围是( )
A. B. C. D.
8、已知表示不超过x的最大整数,例如,,方程的解集为A,集合,且,则实数k的取值范围是( )
A. B.
C. D.
二、多项选择题
9、下列说法正确的是( )
A.在直角坐标平面内,第一、三象限的点的集合为
B.方程的解集为
C.集合与是同一个集合
D.若,则
10、若,则实数m的可能取值为( )
A.4 B.2 C.1 D.-2
11、已知实数a,b,c,其中,,则下列关系中一定成立的是( )
A. B. C. D.
12、已知关于x的不等式的解集是,其中,则下列结论中正确的是( )
A. B. C. D.
三、填空题
13、已知,则的取值范围为________.
14、中国健儿在东京奥运会上取得傲人佳绩,球类比赛获奖多多,其中乒乓球、羽毛球运动备受学生追捧.某校高一(1)班40名学生在乒乓球、羽毛球两个兴趣小组中,每人至少报名参加一个兴趣小组,报名乒乓球兴趣小组的人数比报名羽毛球兴趣小组的人数3倍少4人,且两兴趣小组都报名的学生有8人,则只报名羽毛球兴趣小组的学生有________________人.
15、对于问题“已知关于x的不等式的解集为,解关于x的不等式的”,给出一种解法:由的解集为,得的解集为.即关于x的不等式的解集为.类比上述解法,若关于x的不等式的解集为,则关于x的不等式的解集为______________.
四、双空题
16、,若表示集合中元素的个数,则_________,则_________.
五、解答题
17、设集合,.
(1)若,求a的值;
(2)若,求实数a组成的集合C.
18、已知集合,.
(1)若,求;
(2)若,求m的取值范围.
19、关于x的不等式,关于x的不等式,
(1)记,求A;
(2)若q是p的必要不充分条件,求实数a的取值范围.
20、设.
(1)若不等式对一切实数x恒成立,求实数a的取值范围;
(2)解关于x的不等式.
21、已知bg糖水中有ag糖,往糖水中加入mg糖,(假设全部溶解)糖水更甜了.
(1)请将这个事实表示为一个不等式,证明这个不等式
(3)利用(1)的结论证明命题:“若在中a,b,c分别为角A,B,C所对的边长,则”
22、已知集合A为非空数集,定义:,.
(1)若集合,直接写出集合S、T;
(2)若集合,且,写出一个满足条件的集合A,并说明理由;
(3)若集合,,记为集合A中元素的个数,求的最大值.
参考答案
1、答案:B
解析:全集,
,
故选:B.
2、答案:A
解析:,反之由q推不出p,
所以p是q的充分不必要条件.
故选:A.
3、答案:D
解析:,
因为,所以满足条件的集合B的个数为.
故选:D.
4、答案:B
解析:,
选项A中Venn图中阴影部分表示, 不符合题意;
选项B中Venn图中阴影部分表示, 符合题意;
选项C中Venn图中阴影部分表示, 不符合题意;
选项D中Venn图中阴影部分表示,不符合题意,
故选:B.
5、答案:A
解析:政治书上讲,“有使用价值的东西不一定有价值,有价值的东西一定有使用价值”,
把有使用价值的东西看作集合A,
把有价值的东西看作集合B,则,,.
故选:A.
6、答案:C
解析:依题意可设买大竹子x,每根单价为m,
购买小竹子,每根单价为,所以,
即,即,
因为,
所以,
根据选项,,所以买大竹子30根,每根8元.
故选:C.
7、答案:D
解析: 的几何意义为数轴上的动点x到两定点-2、1的距离和,
则的最小值为.
而关于x的不等式的解集为空集,.
即实数a的取值范围是 .
故选:D.
8、答案:D
解析:由题意可得,解得或,
所以或,
所以,
,
当时,,
由,则,解得;
当 时,,此时 不咸立, 故不取;
当 时,,
则,解得,
综上所述,实数k的取值范围是.
故选:D.
9、答案:AC
解析:对于A,因为 等价于或,
如果则点在第一象限,如果,则点在第三象限,故A正确;
对于B,由于方程的解集等价于,
解得,故解集为,故B错误.
对于C,集合 表示的函数值的取值范围,是数集,同样地, 表示的函数值的取值范围,也是数集,故集合与是同一个集合;C正确;
对于D,,则, 故D错误;
故选:AC.
10、答案:ABD
解析:三个元素中有且只有一个是 3, 要分三类讨论.
当时,,此时,故符合题意;
当时,,此时(注意检验), 不满足集合中元素的互异性, 故舍去;
当时,,经检验 符合题意.
综上可知,或.
故选:ABD.
11、答案:ABD
解析:对于A,,故 A 正确;
对于B,因为,所以,故 B 正确:
对于C,当,,时,,故C错误;
对于D,因为 ,故D正确.
故选:ABD.
12、答案:ACD
解析:
13、答案:
解析:由题意可得,
又 ,由不等式的同向可加性可得.
故答案为:.
14、答案:5
解析:设报名乒乓球兴趣小组的学
生构成集合A,其元素个数为x,报名羽毛球兴趣小组的学生构成集合B, 元素个数为y,
其关系如下:
由题意可知:,解得,
因此只报名羽毛球兴趣小组的学生有人.
故答案为:5.
15、答案:
解析:若关于x的不等式 的解集为 ,
则关于x的不等式 后成不等式中的x用 代入得来,
则可得,
解得,.
故答案为:.
16、答案:11,682
解析:
17、答案:(1)2
(2)
解析:(1)由,解得或,所以,
因为,所以,则,所以;
(2)因为,则,
当时,;
当时,;
当时,,
综上可得集合.
18、答案:(1)
(2)或
解析:(1)由得,,即,
所以
又因为,所以,
所以.
(2)因为,所以,
(i)若,即,则,满足题意;
(ii)若,即,则,
因为,所以,解得;
综上m的取值范围为或.
19、答案:(1)
(2)
解析:(1),解得,
故,
(2),解得,等价于,解得,
记,故,
因为q是p的必要不充分条件,所以A是B的真子集,
所以,解得,
故实数a的取值范围是.
20、答案:(1)
(2)当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为
解析:(1)由题意,不等式对于一切实数x恒成立,
等价于对于一切实数x恒成立.
所以.
(2)不等式等价于.
当即时,不等式可化为,不等式的解集为;
当即时,不等式可化为,不等式的解集为;
当即时,不等式可化为,此时.
综上所述:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
21、答案:(1)见解析
(2)见解析
解析:证明:(1)由题可得
因为,b>a>0,m>0,
所以a-b<0,b+m>0,从而,即.
(2)证明:因为
,
故,所以
22、答案:(1),
(2)
(3)1347
解析:(1)根据题意,由,则,;
(2)由于集合,,且,
所以T中也只包含四个元素,
即,
剩下的,
所以;
(3)设满足题意,其中,
则,
,
,
,
,,
中最小的元素为0,最大的元素为,
,
,
,
实际上当时满足题意,
证明如下:
设,,
则,,
依题意有,即,
故m的最小值为674,于是当时,A中元素最多,
即时满足题意,
综上所述,集合A中元素的个数的最大值是1347.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知全集,,则( )
A. B. C. D.
2、设四边形ABCD为矩形,四边形ABCD为平行四边形,p是q的________条件( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、集合,若,则满足条件的集合B的个数为( )
A.4 B.5 C.7 D.8
4、已知集合,,则下列Venn图中阴影部分可以表示集合的是( )
A. B.
C. D.
5、政治书上讲,“有使用价值的东西不一定有价值,有价值的东西一定有使用价值”,如果把有使用价值的东西看作集合A,把有价值的东西看作集合B,那么它们的关系是( )
A. B. C. D.
6、我国经典数学名著《九章算术》中有这样的一道题:今有出钱五百七十六,买竹七十八,欲其大小率之,向各几何?其意是:今有人出了576钱,买竹子78根,拟分大 小两种竹子为单位进行计算,每根大竹子比小竹子贵1钱,问买大 小竹子各多少根?每根竹子单价各是多少钱?则在这个问题中大竹子每根的单价可能为( )
A.6钱 B.7钱 C.8钱 D.9钱
7、若关于x的不等式的解集为空集,则实数a的取值范围是( )
A. B. C. D.
8、已知表示不超过x的最大整数,例如,,方程的解集为A,集合,且,则实数k的取值范围是( )
A. B.
C. D.
二、多项选择题
9、下列说法正确的是( )
A.在直角坐标平面内,第一、三象限的点的集合为
B.方程的解集为
C.集合与是同一个集合
D.若,则
10、若,则实数m的可能取值为( )
A.4 B.2 C.1 D.-2
11、已知实数a,b,c,其中,,则下列关系中一定成立的是( )
A. B. C. D.
12、已知关于x的不等式的解集是,其中,则下列结论中正确的是( )
A. B. C. D.
三、填空题
13、已知,则的取值范围为________.
14、中国健儿在东京奥运会上取得傲人佳绩,球类比赛获奖多多,其中乒乓球、羽毛球运动备受学生追捧.某校高一(1)班40名学生在乒乓球、羽毛球两个兴趣小组中,每人至少报名参加一个兴趣小组,报名乒乓球兴趣小组的人数比报名羽毛球兴趣小组的人数3倍少4人,且两兴趣小组都报名的学生有8人,则只报名羽毛球兴趣小组的学生有________________人.
15、对于问题“已知关于x的不等式的解集为,解关于x的不等式的”,给出一种解法:由的解集为,得的解集为.即关于x的不等式的解集为.类比上述解法,若关于x的不等式的解集为,则关于x的不等式的解集为______________.
四、双空题
16、,若表示集合中元素的个数,则_________,则_________.
五、解答题
17、设集合,.
(1)若,求a的值;
(2)若,求实数a组成的集合C.
18、已知集合,.
(1)若,求;
(2)若,求m的取值范围.
19、关于x的不等式,关于x的不等式,
(1)记,求A;
(2)若q是p的必要不充分条件,求实数a的取值范围.
20、设.
(1)若不等式对一切实数x恒成立,求实数a的取值范围;
(2)解关于x的不等式.
21、已知bg糖水中有ag糖,往糖水中加入mg糖,(假设全部溶解)糖水更甜了.
(1)请将这个事实表示为一个不等式,证明这个不等式
(3)利用(1)的结论证明命题:“若在中a,b,c分别为角A,B,C所对的边长,则”
22、已知集合A为非空数集,定义:,.
(1)若集合,直接写出集合S、T;
(2)若集合,且,写出一个满足条件的集合A,并说明理由;
(3)若集合,,记为集合A中元素的个数,求的最大值.
参考答案
1、答案:B
解析:全集,
,
故选:B.
2、答案:A
解析:,反之由q推不出p,
所以p是q的充分不必要条件.
故选:A.
3、答案:D
解析:,
因为,所以满足条件的集合B的个数为.
故选:D.
4、答案:B
解析:,
选项A中Venn图中阴影部分表示, 不符合题意;
选项B中Venn图中阴影部分表示, 符合题意;
选项C中Venn图中阴影部分表示, 不符合题意;
选项D中Venn图中阴影部分表示,不符合题意,
故选:B.
5、答案:A
解析:政治书上讲,“有使用价值的东西不一定有价值,有价值的东西一定有使用价值”,
把有使用价值的东西看作集合A,
把有价值的东西看作集合B,则,,.
故选:A.
6、答案:C
解析:依题意可设买大竹子x,每根单价为m,
购买小竹子,每根单价为,所以,
即,即,
因为,
所以,
根据选项,,所以买大竹子30根,每根8元.
故选:C.
7、答案:D
解析: 的几何意义为数轴上的动点x到两定点-2、1的距离和,
则的最小值为.
而关于x的不等式的解集为空集,.
即实数a的取值范围是 .
故选:D.
8、答案:D
解析:由题意可得,解得或,
所以或,
所以,
,
当时,,
由,则,解得;
当 时,,此时 不咸立, 故不取;
当 时,,
则,解得,
综上所述,实数k的取值范围是.
故选:D.
9、答案:AC
解析:对于A,因为 等价于或,
如果则点在第一象限,如果,则点在第三象限,故A正确;
对于B,由于方程的解集等价于,
解得,故解集为,故B错误.
对于C,集合 表示的函数值的取值范围,是数集,同样地, 表示的函数值的取值范围,也是数集,故集合与是同一个集合;C正确;
对于D,,则, 故D错误;
故选:AC.
10、答案:ABD
解析:三个元素中有且只有一个是 3, 要分三类讨论.
当时,,此时,故符合题意;
当时,,此时(注意检验), 不满足集合中元素的互异性, 故舍去;
当时,,经检验 符合题意.
综上可知,或.
故选:ABD.
11、答案:ABD
解析:对于A,,故 A 正确;
对于B,因为,所以,故 B 正确:
对于C,当,,时,,故C错误;
对于D,因为 ,故D正确.
故选:ABD.
12、答案:ACD
解析:
13、答案:
解析:由题意可得,
又 ,由不等式的同向可加性可得.
故答案为:.
14、答案:5
解析:设报名乒乓球兴趣小组的学
生构成集合A,其元素个数为x,报名羽毛球兴趣小组的学生构成集合B, 元素个数为y,
其关系如下:
由题意可知:,解得,
因此只报名羽毛球兴趣小组的学生有人.
故答案为:5.
15、答案:
解析:若关于x的不等式 的解集为 ,
则关于x的不等式 后成不等式中的x用 代入得来,
则可得,
解得,.
故答案为:.
16、答案:11,682
解析:
17、答案:(1)2
(2)
解析:(1)由,解得或,所以,
因为,所以,则,所以;
(2)因为,则,
当时,;
当时,;
当时,,
综上可得集合.
18、答案:(1)
(2)或
解析:(1)由得,,即,
所以
又因为,所以,
所以.
(2)因为,所以,
(i)若,即,则,满足题意;
(ii)若,即,则,
因为,所以,解得;
综上m的取值范围为或.
19、答案:(1)
(2)
解析:(1),解得,
故,
(2),解得,等价于,解得,
记,故,
因为q是p的必要不充分条件,所以A是B的真子集,
所以,解得,
故实数a的取值范围是.
20、答案:(1)
(2)当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为
解析:(1)由题意,不等式对于一切实数x恒成立,
等价于对于一切实数x恒成立.
所以.
(2)不等式等价于.
当即时,不等式可化为,不等式的解集为;
当即时,不等式可化为,不等式的解集为;
当即时,不等式可化为,此时.
综上所述:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
21、答案:(1)见解析
(2)见解析
解析:证明:(1)由题可得
因为,b>a>0,m>0,
所以a-b<0,b+m>0,从而,即.
(2)证明:因为
,
故,所以
22、答案:(1),
(2)
(3)1347
解析:(1)根据题意,由,则,;
(2)由于集合,,且,
所以T中也只包含四个元素,
即,
剩下的,
所以;
(3)设满足题意,其中,
则,
,
,
,
,,
中最小的元素为0,最大的元素为,
,
,
,
实际上当时满足题意,
证明如下:
设,,
则,,
依题意有,即,
故m的最小值为674,于是当时,A中元素最多,
即时满足题意,
综上所述,集合A中元素的个数的最大值是1347.
同课章节目录
