双曲线的几何性质(湖南省湘潭市岳塘区)
文档属性
| 名称 | 双曲线的几何性质(湖南省湘潭市岳塘区) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-07 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
双曲线的简单几何性质
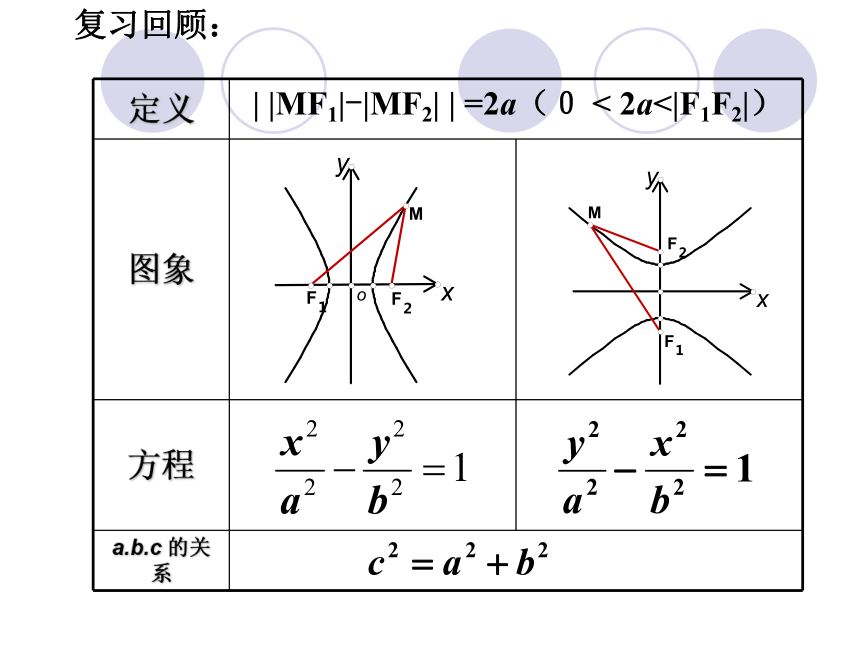
定义
图象
方程
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
复习回顾:
o
Y
X
F1
F2
A1
A2
B2
B1
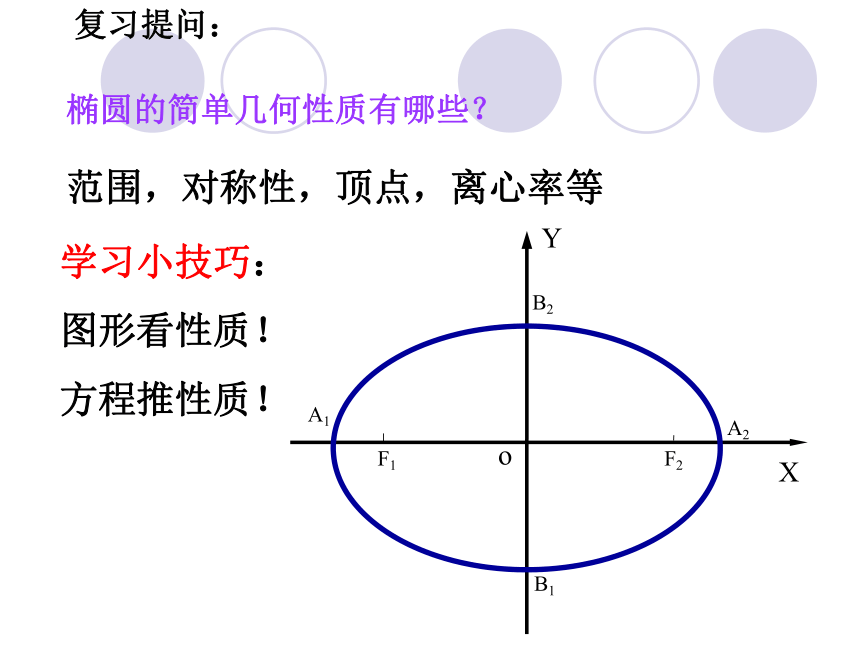
椭圆的简单几何性质有哪些?
复习提问:
范围,对称性,顶点,离心率等
学习小技巧:
图形看性质!
方程推性质!
范围、对称性、顶点、离心率.
渐近线
类比椭圆,探讨双曲线
的几何性质:
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
2、对称性
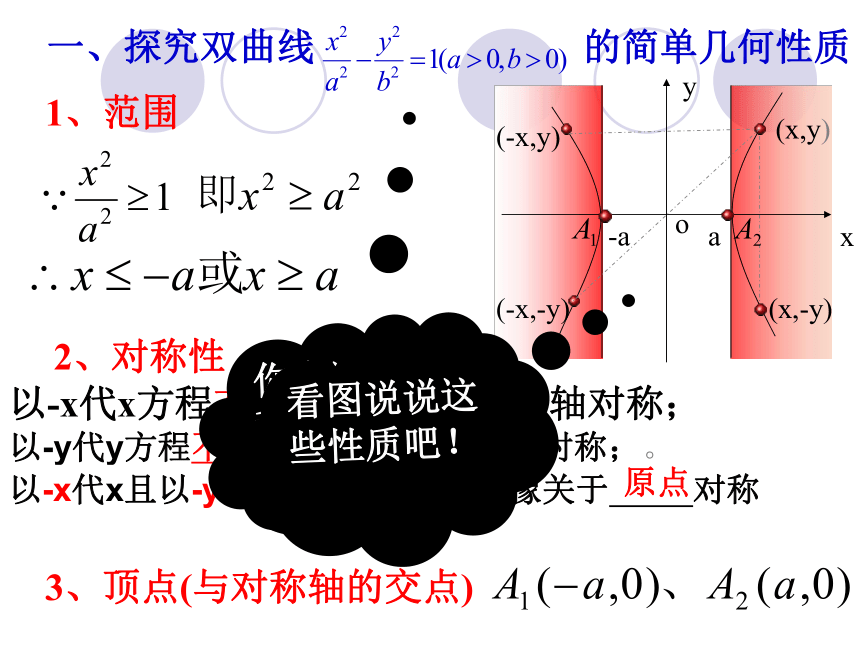
一、探究双曲线 的简单几何性质
1、范围
以-x代x方程不变,故图像关于 轴对称;
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
3、顶点(与对称轴的交点)
以-y代y方程不变,故图像关于 轴对称;。
以-x代x且以-y代y方程不变,故图像关于 对称
y
x
原点
你会通过方程得出这些性质吗?
看图说说这些性质吧!
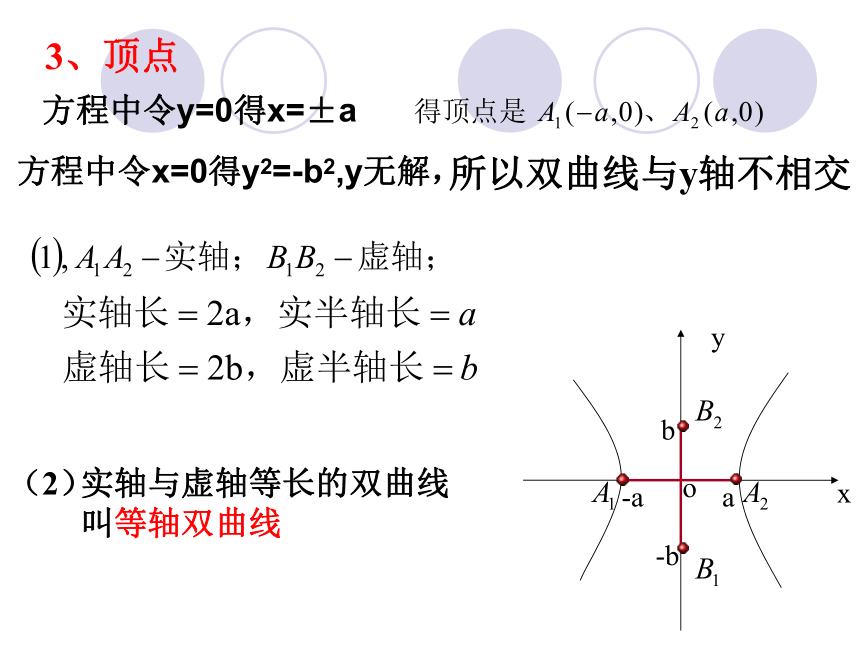
3、顶点
x
y
o
-b
b
-a
a
实轴与虚轴等长的双曲线
叫等轴双曲线
(2)
方程中令y=0得x=±a
方程中令x=0得y2=-b2,y无解,
所以双曲线与y轴不相交
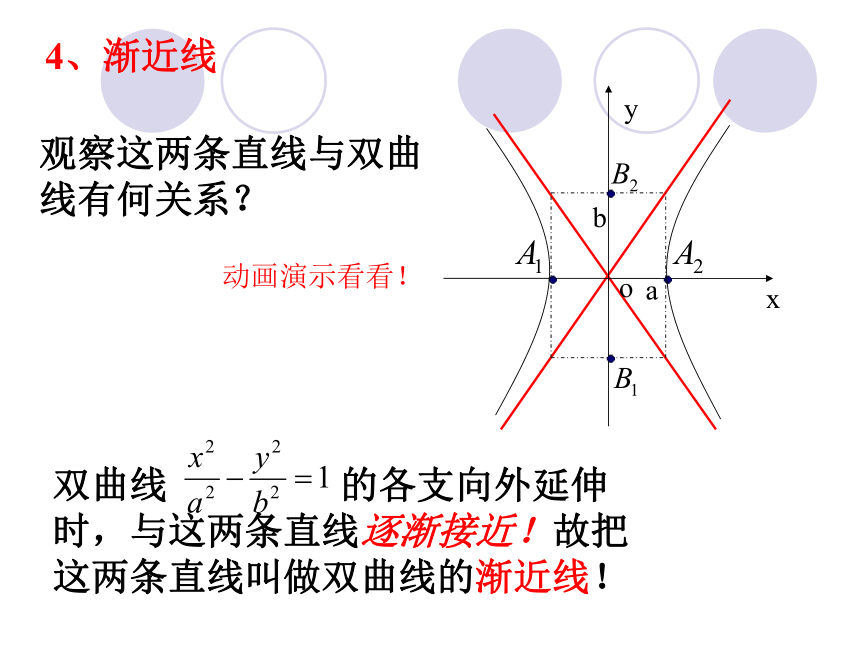
4、渐近线
x
y
o
a
b
动画演示看看!
观察这两条直线与双曲线有何关系?
双曲线 的各支向外延伸时,与这两条直线逐渐接近!故把这两条直线叫做双曲线的渐近线!
4、渐近线
x
y
o
a
b
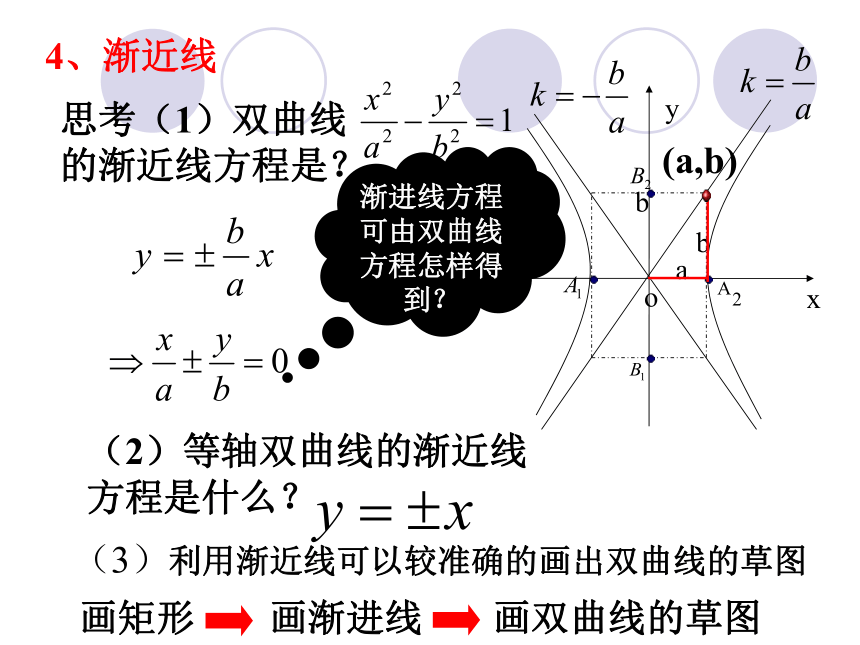
(3)利用渐近线可以较准确的画出双曲线的草图
思考(1)双曲线 的渐近线方程是?
渐进线方程可由双曲线方程怎样得到?
(2)等轴双曲线的渐近线方程是什么?
b
(a,b)
画矩形
画渐进线
画双曲线的草图
5、离心率
离心率。
c>a>0
e >1
(1)定义:
(2)e的范围?
(3)e的含义?
e是表示双曲线开口大小的一个量,e越大开口越大
注意观察演示
为什么?
例1:
1、双曲线 9x2-16y2=144的实半轴长等于 虚半轴长等于 顶点坐
标是 渐近线方是 .
离心率e= 。
4
3
2、离心率e= 是双曲线为等轴双曲线的
条件 。(用“充分条件”“必要条件”“充要条件”填空。)
充要
例2、已知双曲线中心在原点,焦点在x轴上,顶点间的距离是16,离心率 ,求双曲线的标准方程,并求出它的渐近线方程。
一、双曲线 的简单几何性质
学习反思:
二、比较双曲线的几何性质与椭圆的几何性质的异同.
范围,对称性,顶点,离心率,渐进线
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
y
x
O
A2
B2
A1
B1
.
.
F1
F2
y
B2
A1
A2
B1
x
O
.
.
F2
F1
A1(- a,0),A2(a,0)
B1(0,-b),B2(0,b)
F1(-c,0) F2(c,0)
F1(-c,0)
F2(c,0)
关于x轴、y轴、原点对称
A1(- a,0),A2(a,0)
渐进线
无
学习反思:
三、本节课你学到了哪些好的数学学习方法?
“类比学习法,数形结合法”
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。并画出它的草图。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
练一练:
x
y
o
-4
4
3
-3
定义
图象
方程
范围
对称性
顶点
离心率
渐近线
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
一、双曲线的简单几何性质
(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a
关于坐标轴、原点对称(实轴、虚轴、中心)
小结:
作业:P61 A 3,4
x
y
o
思考1:如图,曲线C1,C2是椭圆;曲线C3,C4是双曲线,它们对应的离心率分别为e1,e2,e3,e4.则有( )
B
思考2:求与椭圆
有共同焦点,渐近线方程为
的双曲线方程。
双曲线的简单几何性质
定义
图象
方程
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
复习回顾:
o
Y
X
F1
F2
A1
A2
B2
B1
椭圆的简单几何性质有哪些?
复习提问:
范围,对称性,顶点,离心率等
学习小技巧:
图形看性质!
方程推性质!
范围、对称性、顶点、离心率.
渐近线
类比椭圆,探讨双曲线
的几何性质:
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
2、对称性
一、探究双曲线 的简单几何性质
1、范围
以-x代x方程不变,故图像关于 轴对称;
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
3、顶点(与对称轴的交点)
以-y代y方程不变,故图像关于 轴对称;。
以-x代x且以-y代y方程不变,故图像关于 对称
y
x
原点
你会通过方程得出这些性质吗?
看图说说这些性质吧!
3、顶点
x
y
o
-b
b
-a
a
实轴与虚轴等长的双曲线
叫等轴双曲线
(2)
方程中令y=0得x=±a
方程中令x=0得y2=-b2,y无解,
所以双曲线与y轴不相交
4、渐近线
x
y
o
a
b
动画演示看看!
观察这两条直线与双曲线有何关系?
双曲线 的各支向外延伸时,与这两条直线逐渐接近!故把这两条直线叫做双曲线的渐近线!
4、渐近线
x
y
o
a
b
(3)利用渐近线可以较准确的画出双曲线的草图
思考(1)双曲线 的渐近线方程是?
渐进线方程可由双曲线方程怎样得到?
(2)等轴双曲线的渐近线方程是什么?
b
(a,b)
画矩形
画渐进线
画双曲线的草图
5、离心率
离心率。
c>a>0
e >1
(1)定义:
(2)e的范围?
(3)e的含义?
e是表示双曲线开口大小的一个量,e越大开口越大
注意观察演示
为什么?
例1:
1、双曲线 9x2-16y2=144的实半轴长等于 虚半轴长等于 顶点坐
标是 渐近线方是 .
离心率e= 。
4
3
2、离心率e= 是双曲线为等轴双曲线的
条件 。(用“充分条件”“必要条件”“充要条件”填空。)
充要
例2、已知双曲线中心在原点,焦点在x轴上,顶点间的距离是16,离心率 ,求双曲线的标准方程,并求出它的渐近线方程。
一、双曲线 的简单几何性质
学习反思:
二、比较双曲线的几何性质与椭圆的几何性质的异同.
范围,对称性,顶点,离心率,渐进线
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
y
x
O
A2
B2
A1
B1
.
.
F1
F2
y
B2
A1
A2
B1
x
O
.
.
F2
F1
A1(- a,0),A2(a,0)
B1(0,-b),B2(0,b)
F1(-c,0) F2(c,0)
F1(-c,0)
F2(c,0)
关于x轴、y轴、原点对称
A1(- a,0),A2(a,0)
渐进线
无
学习反思:
三、本节课你学到了哪些好的数学学习方法?
“类比学习法,数形结合法”
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。并画出它的草图。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
练一练:
x
y
o
-4
4
3
-3
定义
图象
方程
范围
对称性
顶点
离心率
渐近线
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
一、双曲线的简单几何性质
(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a
关于坐标轴、原点对称(实轴、虚轴、中心)
小结:
作业:P61 A 3,4
x
y
o
思考1:如图,曲线C1,C2是椭圆;曲线C3,C4是双曲线,它们对应的离心率分别为e1,e2,e3,e4.则有( )
B
思考2:求与椭圆
有共同焦点,渐近线方程为
的双曲线方程。
