圆周角定理

(共17张PPT)
观察
※ 圆周角
顶点在圆上,它的两边分别
与圆还有另一个交点,像这
样的角,叫做圆周角.
判断条件
｛
（1）顶点在圆上；
（2）两边应与圆相交。
议一议
想一想
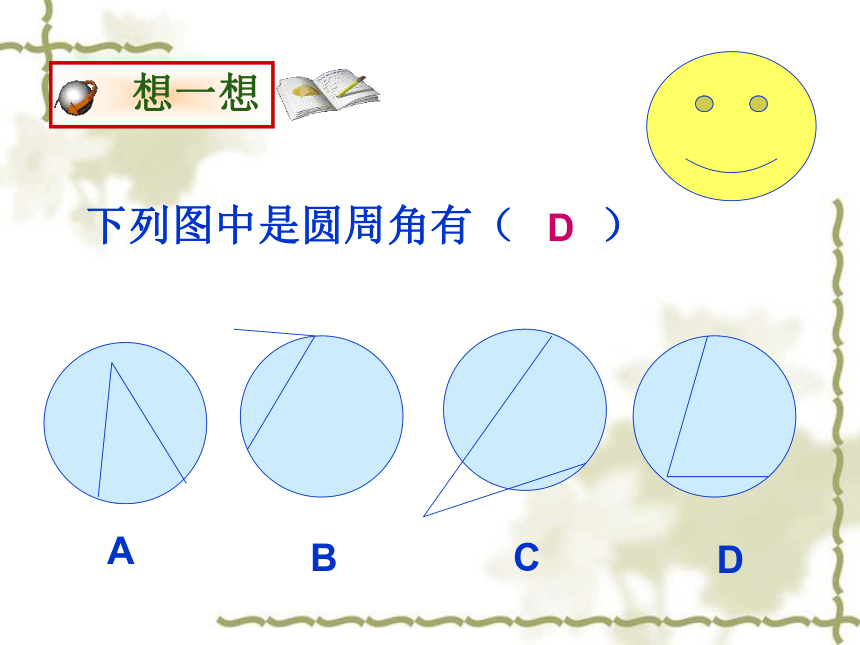
下列图中是圆周角有（ ）
D
C
B
A
D
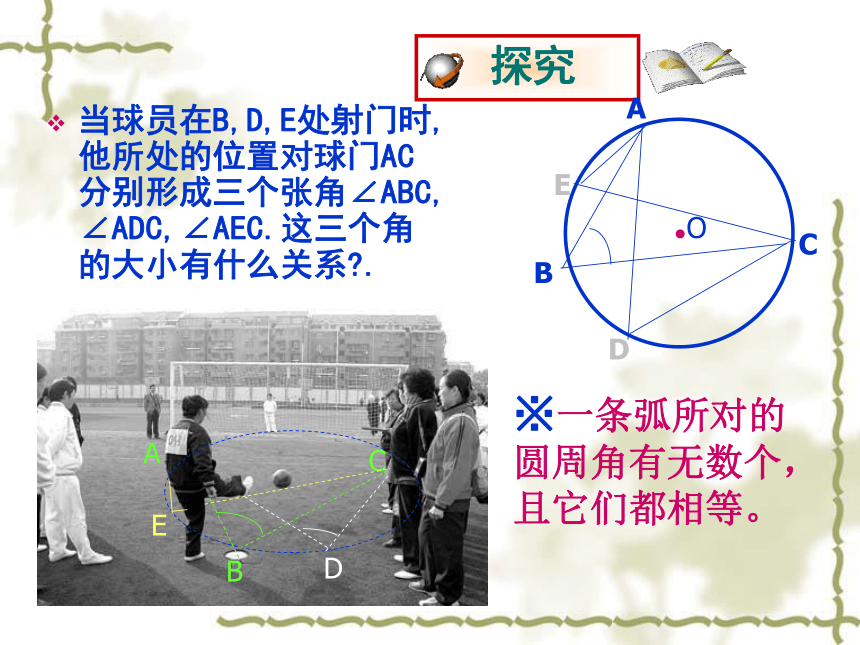
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系 .
探究
●O
B
A
C
B
A
C
D
E
D
E
※一条弧所对的
圆周角有无数个，
且它们都相等。
探究
演示
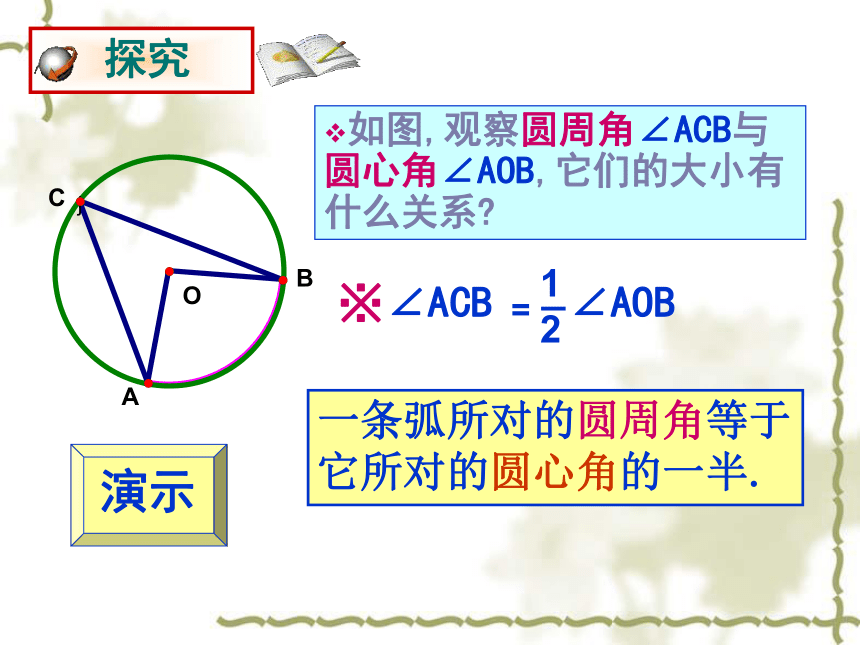
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系
∠AOB
∠ACB
=
1
2
_
※
一条弧所对的圆周角等于
它所对的圆心角的一半.
圆周角和圆心角的关系
议一议
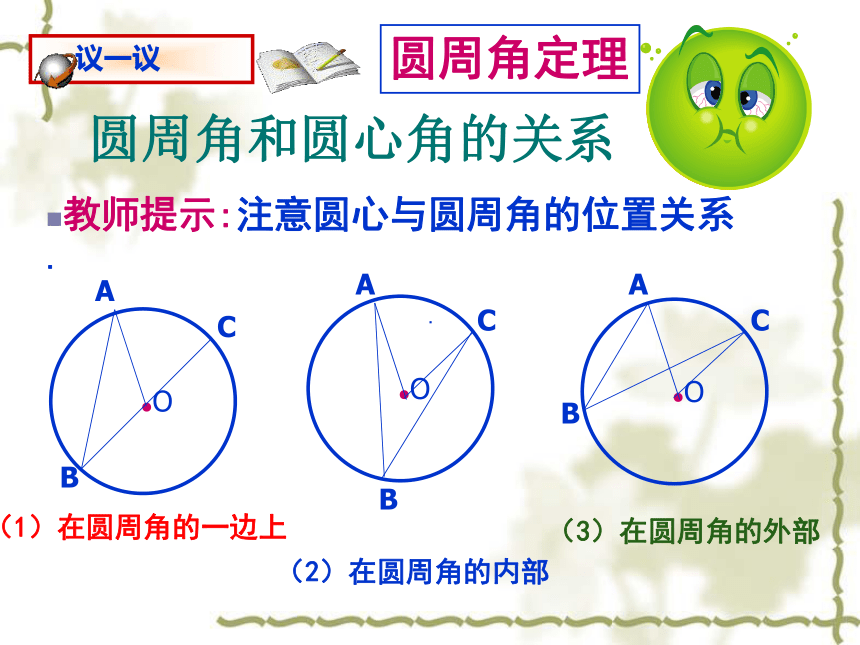
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
·
圆周角定理
（1）在圆周角的一边上
（2）在圆周角的内部
（3）在圆周角的外部
●O
c
A
B
1. 当圆心在圆周角的一边上时。
证明：如图
OA=OC
∠A=∠C
又∠BOC=∠A+∠C
即∠A= ∠BOC
∠BOC=2∠A
一条弧所对的圆周角等于它所对的圆心角的一半.
2.当圆心在圆周角的内部时,
●O
A
B
C
老师提示:能否转化为1的情况
一条弧所对的圆周角等于它所对的圆心角的一半.
∴ ∠ABC = ∠AOC.
∠BAD = ∠BOD,∠CAD = ∠COD
∠BAD+ ∠CAD = (∠BOD + ∠COD)
证明：如图
过点A作直径AD.由1可得:
。
。
D
3.当圆心在圆周角的外部时.留做作业.
随堂练习
在同圆或等圆中，同弧或等弧所对的圆周角都相等，等于它所对的圆心角的一半。
归纳
1.如图,在⊙O中,
∠BOC=50°,求∠A的大小.
●O
B
A
C
※ 1.如图相等的圆周角有那些？
。
A
B
C
D
4
5 6
7 8
1
2
3
解：∠1= ∠4 ， ∠2= ∠8 ，
∠3= ∠6 ， ∠5= ∠7
解: ∠A = ∠BOC = 25°.
探究
观察
※一条弦所对的圆周角有无数个，顶点在劣弧或优弧上的圆周角分别相等。这条弦两侧的圆周角互补。
A
B
C
D
E
如图: ∠D=∠E,
∠D+∠C=180°
∠E+∠C=180°
如图：弦AB所对圆周角有那些？
它们有什么关系？
随堂练习
一条弦长等于圆的半径，求它所对圆周角的度数。
※解：如图
弦长等于圆的半径
OA=OB=AB
∠AOB=60
∠ACB= ∠AOB =30
∠ACB+ ∠ADB=180
∠ADB=180 - ∠ACB=150
°
°
°
°
°
o
A
B
C
D
。
独立作业
★P94 4,11
白水中学
刘和平