2015年高考数学理科押题 精粹
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2015年高考押题 精粹
数学理科
本卷共60题,三种题型:选择题、填空题和解答题。选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)
1. 已知全集, 集合, , 则集合可以表示为( )
A. B. C. D.
2. 集合 ,则集合C中的元素个数为( )
A.3 B.4 C.11 D.12
3. 设集合,,则=( )
A. B. C. D.
4. 若(其中为虚数单位),则等于( )
A.1 B. C. D.
5. 若复数(为虚数单位)是纯虚数,则实数的值为( )
A. B. C. D.
6. 复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7. 已知向量,若,则( )
A. B. C. D.
8. 已知为的边的中点,所在平面内有一个点,满足,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
9.中,,AB=2,AC=1,D是边BC上的一点(包括端点),则 的取值范围是( )
A. [1,2] B.[0,1] C.[0,2] D. [﹣5,2]
10.已知命题:,,命题:,,则下列说法中正确的是( )
A.命题是假命题 B.命题是真命题
C.命题是真命题 D.命题是假命题
11.命题“,”的否定是( )
A., B.,
C., D.,
12.命题:关于的方程有三个实数根;命题:;则命题成立时命题成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
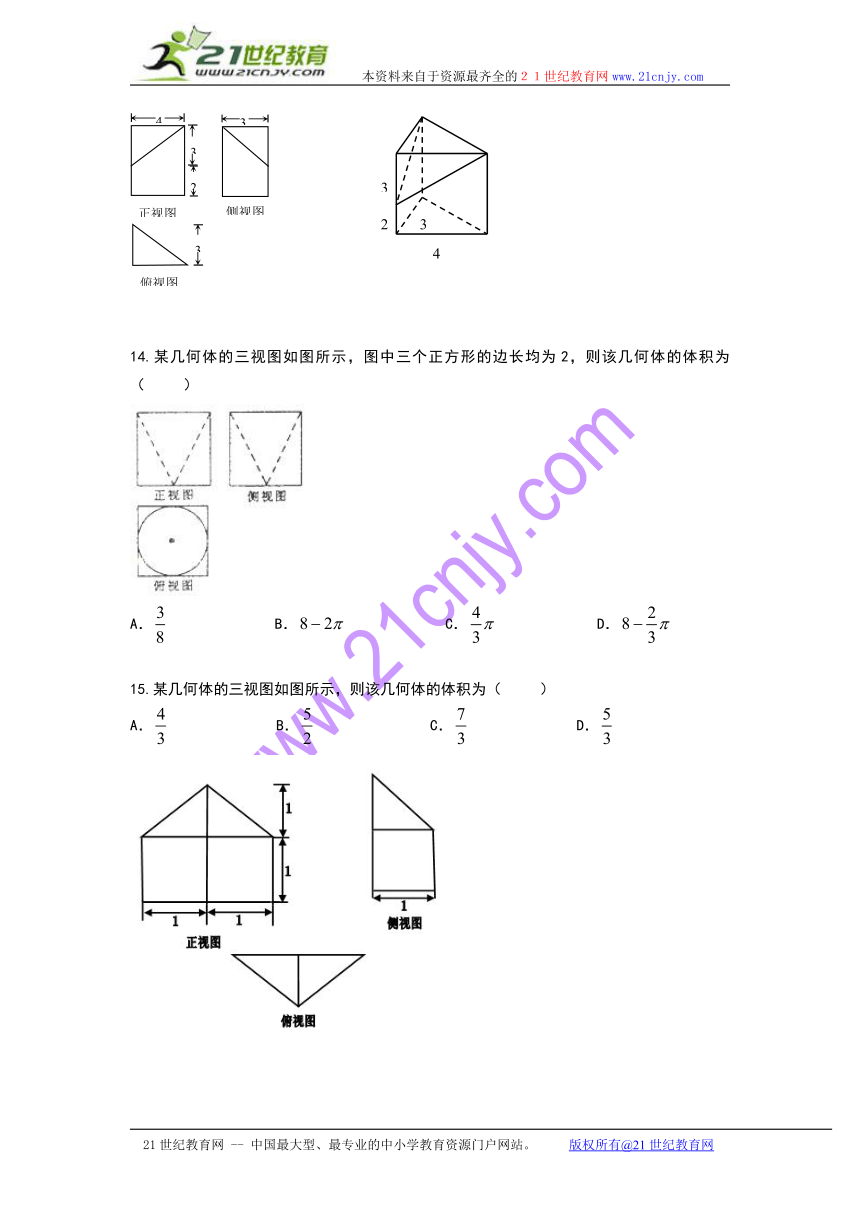
13.若某几何体的三视图如右图所示,则此几何体的体积等于( )
A. B. C. D.
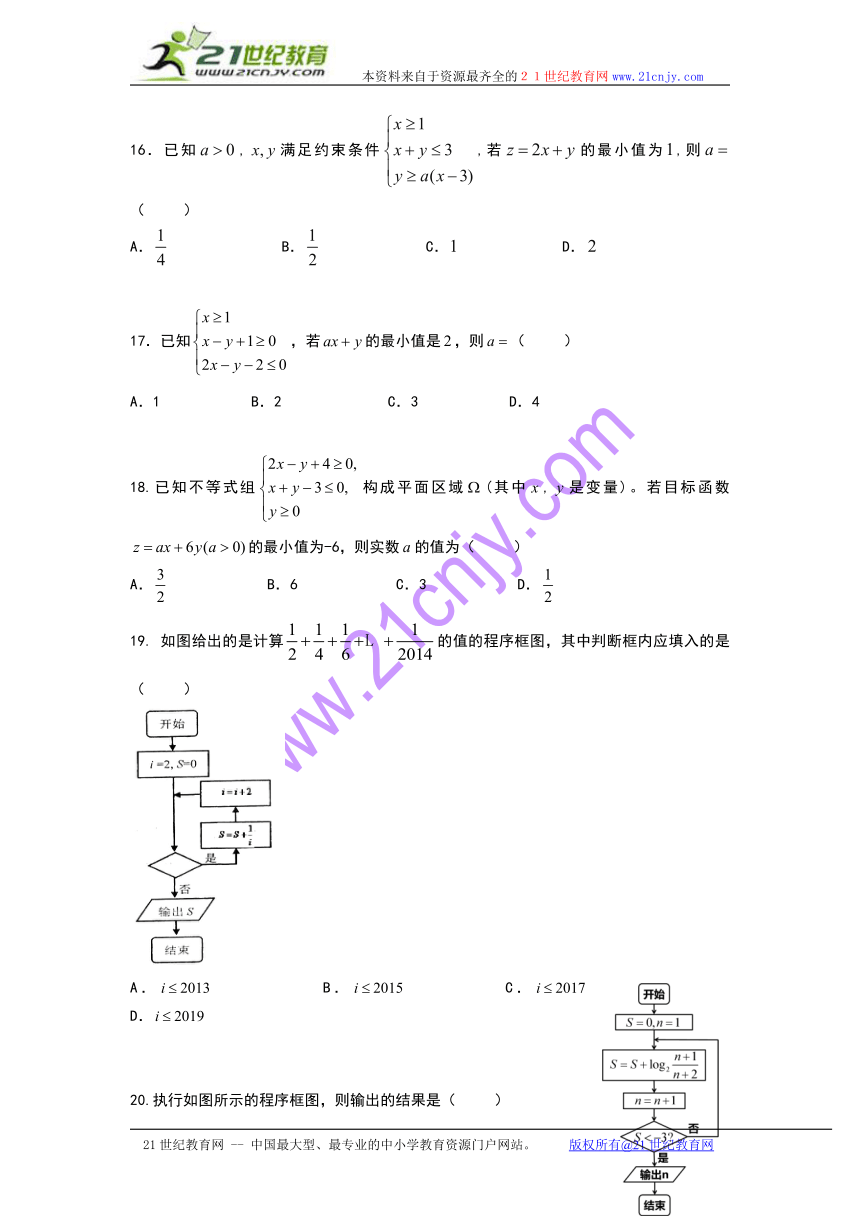
14.某几何体的三视图如图所示,图中三个正方形的边长均为2,则该几何体的体积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
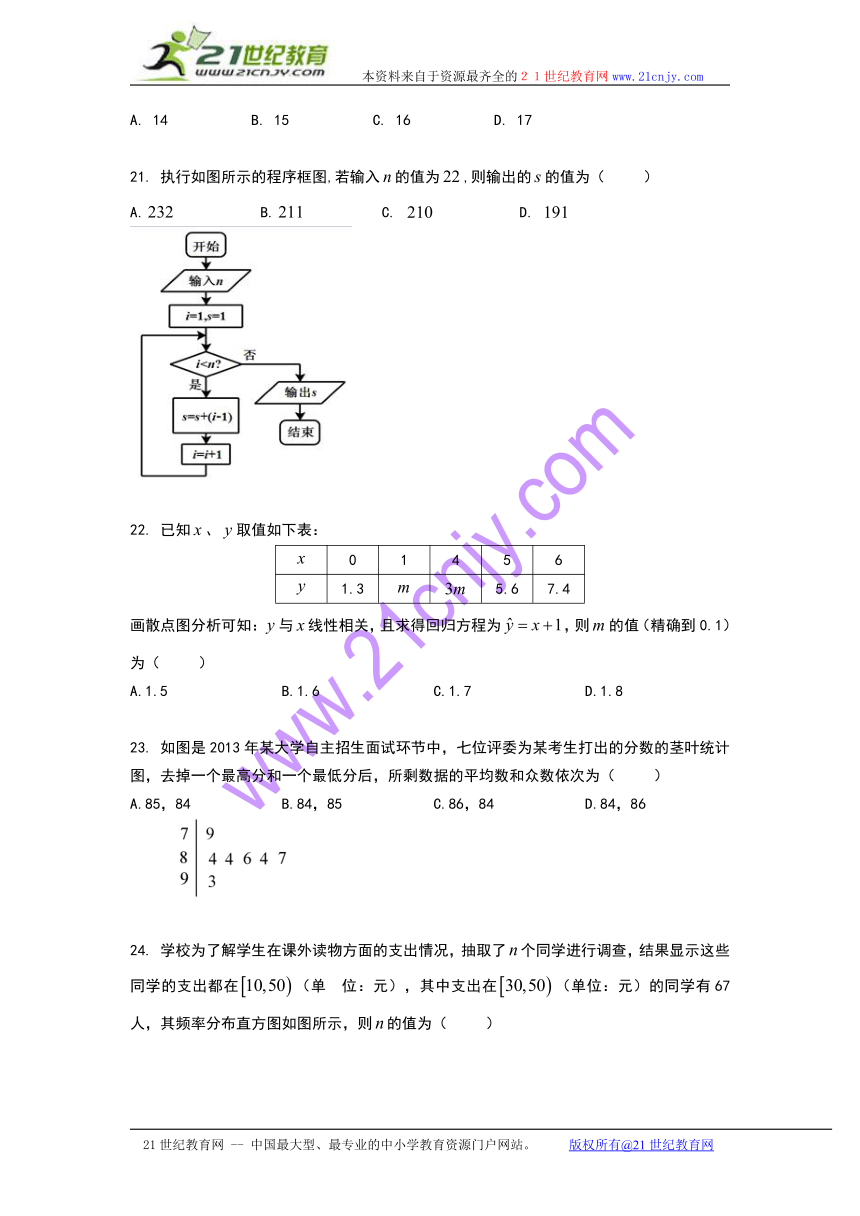
15.某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
( http: / / www.21cnjy.com )
16.已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
17.已知,若的最小值是,则( )
A.1 B.2 C.3 D.4www.21-cn-jy.com
18.已知不等式组构成平面区域(其中,是变量)。若目标函数的最小值为-6,则实数的值为( )【来源:21·世纪·教育·网】
A. B.6 C.3 D.
19. 如图给出的是计算的值的程序框图,其中判断框内应填入的是( )
( http: / / www.21cnjy.com )
A. B. C. D.
20.执行如图所示的程序框图,则输出的结果是( )
A. 14 B. 15 C. 16 D. 17
21. 执行如图所示的程序框图,若输入的值为,则输出的的值为( )
A. B. C. D.
( http: / / www.21cnjy.com )
22. 已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
23. 如图是2013年某大学自主招生面 ( http: / / www.21cnjy.com )试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
A.85,84 B.84,85 C.86,84 D.84,86
( http: / / www.21cnjy.com )
24. 学校为了解学生在课外读物方面的支出情况,抽取了个同学进行调查,结果显示这些同学的支出都在(单 位:元),其中支出在(单位:元)的同学有67人,其频率分布直方图如图所示,则的值为( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.100 B.120 C.130 D.390
25. 若,是第三象限的角,则( )
A. B. C. D.
26. 在中,若的形状一定是( )
A.等边三角形 B.不含的等腰三角形 C.钝角三角形 D.直角三角形
27. 已知,函数在上单调递减,则的取值范围是( )
A. B. C. D.
28. 函数的最小正周期为,为了得到的图象,只需将函数的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
29. 在中,是边上的一点,,的面积为,则的长为( )
A. B. C. D.
30. 已知函数的最小正周期为,最小值为,将函数的图像向左平移(>0)个单位后,得到的函数图形的一条对称轴为,则的值不可能为( )
A. B. C. D.
31. 已知双曲线的离心率为,则的值为( )
A. B. C. D.
32. 如图过拋物线的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )
A. B
C. D.[]
33. 椭圆M: 左右焦点分别为,,P为椭圆M上任一点且 最大值取值范围是,其中,则椭圆离心率e取值范围为 ( )【版权所有:21教育】
A. B. C. D.
34. 已知函数,则函数的大致图像为( ) ( http: / / www.21cnjy.com )
35. 已知函数,则关于的方程的实根个数不可能为( )
A.个 B.个 C.个 D.个
36. 设定义在D上的函数在点处的切线方程为,当时,若在D内恒成立,则称P为函数的“类对称点”,则的“类对称点”的横坐标是( )
A.1 B. C.e D.
二、填空题(12个小题)
37. 二项式的展开式中的常数项是________.
38. 有4名优秀学生,,,全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有 种.
39.设,则二项式展开式中含项的系数是_____
40. 如图,设是图中边长为4的正方形区域,是内函数图象下方的点构成的区域.在内随机取一点,则该点落在中的概率为 。
( http: / / www.21cnjy.com )
41. 随机向边长为5,5,6的三角形中投一点P,则点P到三个顶点的距离都不小于1的概率是 。
42. 一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当有两个数
字的和等于第三个数字时称为“有缘数”(如213,134等),若,且a,
b,c互不相同,则这个三位数为”有缘数”的概率是_________。
43. 是同一球面上的四个点,其中是正三角形, ⊥平面,,则该球的表面积为_________。
44. 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥. 如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该半球的体积为 。
( http: / / www.21cnjy.com )
45. 已知四棱锥中,底面为矩形,且中心为,,,则该四棱锥的外接球的体积为 。
46. 已知等差数列前项和为,且满足,则数列的公差为 。
47.已知为数列的前项和,且满足,,则 。
48. 已知数列的前n项和,若不等式对恒成立,则整数的最大值为 。
三、解答题(18个小题)
49. 在中,内角的对边分别为已知.
(I)求的值; (II)若,,求的面积。
50. 在△ABC中,a,b,c是其三个内角A,B,C的对边,且.
(Ⅰ)求角C的大小;
(Ⅱ)设,求△ABC的面积S的最大值。
51. 已知数列中,,其前项的和为,且满足.
(Ⅰ) 求证:数列是等差数列;(Ⅱ) 证明:当时,.
52. 第117届中国进出品商品交易会(简 ( http: / / www.21cnjy.com )称2015年春季广交会)将于2015年4月15日在广州举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:cm),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”。
( http: / / www.21cnjy.com )
(Ⅰ)计算男志愿者的平均身高和女志愿者身高的中位数(保留一位小数)。
(Ⅱ)若从所有“高个子”中选3名志愿者,用表示所选志愿者中为女志愿者的人数,试写出的分布列,并求的数学期望。【来源:21cnj*y.co*m】
53. 某学校从参加2015年迎新百科知识 ( http: / / www.21cnjy.com )竞赛的同学中,选取40名同学,将他们的成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题。
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)从频率分布直方图中,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
( http: / / www.21cnjy.com )
54. 某市工业部门计划度所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行问卷调查,结果如下表:21教育网
支持 不支持 合计
中型企业 80 40 120
小型企业 240 200 440
合计 320 240 560
(Ⅰ)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?21cnjy.com
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出12家,然后从这12家中选出9家进行奖励,分别奖励中、小企业每家50万元、10万元。记表示所发奖励的钱数,求的分布列和数学期望:
附:
0.050 0.025 0.010
3.841 5.024 6.635
55.如图,四棱锥,侧面是边长为的正三角形,且与底面垂直,底面是的菱形,为棱上的动点,且()。
(Ⅰ) 求证:;(Ⅱ) 试确定的值,使得二面角的平面角余弦值为。
( http: / / www.21cnjy.com )
56. 如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD.
( http: / / www.21cnjy.com )
(I)证明:DC1⊥BC;
(II)求二面角A1-BD-C1的大小.
57. 已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(I)求证:平面;
(II)设为直线与平面所成的角,求的值;
(Ⅲ)设为中点,在边上求一点,使平面,求的值.
58. 椭圆的离心率为,其左焦点到点的距离为.
(I)求椭圆的标准方程;
(II) 若直线与椭圆相交于两点(不是左右顶点),且以为直径的圆过椭圆的右顶点,求证:直线过定点,并求出该定点的坐标.
59. 已知椭圆 的两个焦点,,动点P在椭圆上,且使得的点P恰有两个,动点P到焦点的距离的最大值为。
(I)求椭圆的方程;
(II)如图,以椭圆的长轴为直径作圆,过直线上的动点T作圆的两条切线,设切点分别为A,B,若直线AB与椭圆交于不同的两点C,D,求的取值范围。 ( http: / / www.21cnjy.com )
60. 已知抛物线的焦点到准线的距离为2。
(Ⅰ)求的值;
(Ⅱ)如图所示,直线与抛物线相交于,两点,为抛物线上异于,的一点,且轴,过作的垂线,垂足为,过作直线交直线BM于点,设的斜率分别为,且。
① 线段的长是否为定值 若是定值,请求出定值;若不是定值,请说明理由;
② 求证:四点共圆.
( http: / / www.21cnjy.com )
61. 已知,其中.
(Ⅰ)求的单调递减区间;
(Ⅱ)若在上的最大值是,求的取值范围.
62. 已知函数为自然对数的底数)
(I)求函数的最小值;
(II)若≥0对任意的∈R恒成立,求实数a的值;
(III)在(II)的条件下,证明:
63. 已知函数.
(Ⅰ)当时,求在处的切线方程;
(Ⅱ)设函数,
①若函数有且仅有一个零点时,求的值;
②在①的条件下,若,,求的取值范围。
64. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
A.选修4-1:几何证明选讲
如图所示,为圆的直径,,为
圆的切线,,为切点.
(Ⅰ)求证: ;
(Ⅱ)若圆的半径为2,求的值.
B.选修4-4:坐标系与参数方程
已知在直角坐标系中,圆的参数方程为(为参数).
(Ⅰ)以原点为极点、轴正半轴为极轴建立极坐标系,求圆的极坐标方程;
(Ⅱ)已知,圆上任意一点,求△面积的最大值.
C.选修4-5:不等式选讲
已知函数且的解集为
(Ⅰ)求k的值;
(Ⅱ)若是正实数,且,求证:。
65. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑
A.选修4—1:几何证明选讲
如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
(I)求证:DC是⊙O的切线;
(II)求证:AM·MB=DF·DA.
B.选修4-4:坐标系与参数方程
极坐标系与直角坐标系有相同的长度单位,以原点为极点,以轴正半轴为极轴.已知直线的参数方程为(为参数),曲线的极坐标方程为.
(I)求的直角坐标方程;
(II)设直线与曲线交于两点,求弦长.
C.选修4-5:不等式选讲
已知函数
(I)若,解不等式;
(II)如果,求的取值范围.
66. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑
A. 选修4—1:几何证明选讲
如图,四边形ABCD内接于圆.
求对角线BD、AC的长.
B.选修4—4:坐标系与参数方程
已知曲线的极坐标方程为,以极点为坐标原点,极轴为轴正半轴建立
平面直角坐标系,直线的参数方程为(为参数)
(I)把曲线的极坐标方程化为直角坐标方程,把直线的参数方程化为普通方程;
(II)求直线被曲线截得的线段的长.
C.选修4—5:不等式选讲
已知a,b∈,a+b=1,,∈.
(1)求的最小值;
(2)求证:.
参考答案
一、选择题(36个小题)
1.答案:B
解析:有元素1,2的是,分析选项则只有B符合。
2. 答案:C
解析:,故选C。
3. 答案:C
解析:集合,。
4. 答案:C
解析:化简得,则=,故选C。
5. 答案:A
解析:,所以。
6. 答案:D
解析:根据复数的运算可知,所以复数的坐标为,所以正确选项为D。
7. 答案:B
解析:,
。
8. 答案:C
解析:如图,四边形是平行四边形,D为边BC的中点,所以D为边的中点,的值为1。
9. 答案:D
解析:∵D是边BC上的一点(包括端点),
∴可设
,,,
的取值范围是。
10. 答案:C
解析:命题为真命题.对命题,当时,,故为假命题,为真命题.所以C正确。
11. 答案:C
解析:命题“,” 是特称命题,则它的否定是全称命题,即。
12. 答案:B
解析:由方程,易知函数是上的奇函数,由的图像可知,函数在上的最大值是1,根据图像的对称性知函数在上的最小值为-1,又函数的图像与轴有3个交点,那么原方程有3个实数根的充要条件是,而,所以选择B。21*cnjy*com
13. 答案:C
解析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,
如图,故选。
14. 答案:D
解析:由三视图可知此几何体是:棱长为2 的正方体挖去了一个圆锥而形成的新几何体,其体积为,故选 D。
15. 答案:A
解析:该几何体是下面是一个三棱柱,上面是一个有一个侧面垂直于底面的三棱锥。其体积为。
16. 答案:B
解析:依题意可以画出不等式表示的图形,当过点时取最小值,即2-2=1,=。
17. 答案:B
解析:由已知得线性可行域如图所示,则的最小值为,若,则为最小值最优解,∴,若,则为最小值最优解,不合题意,故选B。
( http: / / www.21cnjy.com )
18. 答案:C
解析:不等式组表示的平面区域如图阴影部分所示,因为,故。可知在C点处取得最小值,联立解得即,故,解得。
( http: / / www.21cnjy.com )
19. 答案:B
解析:由程序知道,都应该满足条件,不满足条件,故应该选择B。
20. 答案:C
解析:由程序框图可知,从到得到,因此将输出
. 故选C。
21. 答案:B
解析:第一次运行时,;第二次运行时,;
第三次运行时,;第四次运行时,;
第五次运行时,;…,以此类推,
直到,程序才刚好不满足,故输出.故选B。
22. 答案:C
解析:将代入回归方程为可得,则,解得,即精确到0.1后的值为. 故选C。
23. 答案:A
解析:去掉一个最高分和一个最低分后,所剩数据为84,84,86,84,87,平均数为,众数为84. 故选A。
24. 答案:A
解析:支出在的同学的频率为,。
25. 答案:B
解析:由题意,因为是第三象限的角,所以,
因此。
26. 答案:D
解析:∵sin(A-B)= ( http: / / www.21cnjy.com )1+2cos(B+C)sin(A+C),∴sin(A-B)=1-2cosAsinB,
∴sinAcosB-cosAsinB=1-2cosAsinB,∴sinAcosB+cosAsinB=1,
∴sin(A+B)=1,∴A+B=90°,∴△ABC是直角三角形。
27. 答案:A
解析:结合特殊值,求解三角函数的递减区间,并验证结果.取,,其减区间为,显然,排除;取,,其减区间为,显然,排除.选。
28. 答案:C
解析:因为函数的最小正周期为,所以,则,则用换x即可得到的图像,所以向左平移个单位长度,则选C。
29. 答案:D
解析:因为,可得,即,所以.在中,由余弦定理,解得,所以,所以,
在中,由正弦定理可知,可得。
30. 答案:B
解析:,依题意,,所以,因为,解得,故,故,所以,即。将函数的图片向左平移(>0)个单位后得到,因为函数的一条对称轴为。故,解得,观察可知,选B。 21*cnjy*com
31. 答案:B
解析:依题意,,。
32. 答案:D
解析:如图分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则由已知得:|BC|=2a,由定义得:|BD|=a,故∠BCD=30°,
在直角三角形ACE中,∵|AF|=3,|AC|=3+3a,∴2|AE|=|AC|
∴3+3a=6,从而得a=1,∵BD∥FG,∴,求得p=,因此抛物线方程为y2=3x。
33. 答案:B
解析:由椭圆定义知,
的最大值为
而最大值取值范围是,所以
于是得到,
故椭圆的离心率的取值范围是,选B。
34. 答案:A
解析:由函数的奇偶性可知函数为非奇非偶函数,所以排除B,C,再令,说明当x为负值时,有小于零的函数值,所以排除D。
35. 答案:A
解析:因为时,=1或=3或=或=-4,则当a=1时或1或3或-4,又因为,则当时只有一个
=-2与之对应其它情况都有两个值与之对应,所以此时所求方程有7个根,当1<a<2时因为函数与y=a有4个交点,每个交点对应两个,则此时所求方程有8个解,当a=2时函数与y=a有3个交点,每个交点对应两个,则此时所求方程有6个解,所以B,C,D都有可能,则选A。
36. 答案:B
解析:由于,则在点P处切线的斜率.
所以切线方程为
,
则,.
当时,在上单调递减,所以当时, 从而有时,;
当时,在上单调递减,所以当时, 从而有时,;
所以在上不存在“类对称点”. 当时,,所以在上是增函数,故
所以是一个类对称点的横坐标. (可以利用二阶导函数为0,求出,则。
二、填空题(12个小题)
37. 答案:45
解析:,则,故常数项为。
38. 答案:36
解析:先从4名优秀学生,,,中选出2名保送到甲,乙,丙3所学校中的某一所,有种方案;然后将剩余的2名优秀学生保送到剩余的2所学校,有种方案;故不同的保送方案共有种。
39. 答案:-192
解析:由于
则含项的系数为。
40. 答案:
解析:由几何概型得,该点落在中的概率为。
41. 答案:
解析:分别以三角形的三个顶点为圆心,1为半径作圆,则在三角形内部且在三圆外部的区域即为与三角形三个顶点距离不小于1的部分,即。
42. 答案:
解析:由1,2,3组成的三位自然数为123,132,213,231,312,321,共6个;
同理由1,2,4组成的三位自然数共6个;
由1,3,4组成的三位自然数也是6个;
由2,3,4组成的三位自然数也是6个.
所以共有6+6+6+6=24个.
由1,2,3组成的三位自然数,共6个”有缘数”.
由1,3,4组成的三位自然数,共6个”有缘数”.
所以三位数为”有缘数”的概率。
43. 答案:32
解析:由题意画出几何体的图形如图,
把A、B、C、D扩展为三棱柱,上下底面中心连线的中点与A的距离为球的半径,
AD=4,AB=2,△ABC是正三角形,所以AE=2,AO=2。
所求球的表面积为:4(2)2=32。
( http: / / www.21cnjy.com )
44. 答案:
解析:设所给半球的半径为,则棱锥的高,底面正方形中有,所以其体积,则,
于是所求半球的体积为。
45. 答案:
解析:因为,故,故;同理,;将四棱锥补成一个长方体,可知该长方体的长宽高分别为,故所求外接球的半径,其体积。
46. 答案:2
解析:∵,∴,∴,又,∴。
47. 答案:2×31007﹣2
解析:由anan+1=3n,得,
∴,
则数列{an}的所有奇数项和偶数项均构成以3为公比的等比数列,
又.
∴。
48. 答案:4
解析:当时,得,;
当时,,两式相减得,得,
所以。
又,所以数列是以2为首项,1为公差的等差数列,,即。
因为,所以不等式,等价于。
记,时,。
所以时,。
所以,所以整数的最大值为4。
三、解答题(18个小题)
49. 解:(Ⅰ)由正弦定理,得
所以
即,
化简得,即因此
(Ⅱ)由的
由及
得,解得,因此
又所以,因此
50. 解:(Ⅰ)∵
,或,
由,知,所以不可能成立,所以,
即,
所以
(Ⅱ)由(Ⅰ),,所以,
即△ABC的面积S的最大值为
51. 解:(Ⅰ)当时,,
,,
从而构成以1为首项,2为公差的等差数列.
(Ⅱ)由(1)可知,,.
当时,.
从而。
52. 解:(1)根据茎叶图可得:
男志愿者的平均身高为
女志愿者身高的中位数为
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,而男志愿者的“高个子”有5人,女志愿者的“高个子”有3人2-1-c-n-j-y
的可能值为0,1,2,3,
故
即的分布列为:
0 1 2 3
P
所以的数学期望
53. 解:(Ⅰ)设分数在内的频率为,根据频率分布直方图,
则有,
可得,所以频率分布直方图如图所示.
( http: / / www.21cnjy.com )
(Ⅱ)平均分:
(Ⅲ)学生成绩在的有人,
在的有人,并且的可能取值是0,1,2。
,;
。
所以的分布列为
0 1 2
21·cn·jy·com
所以。
54. 解:(Ⅰ)K2=≈5.657,因为5.657>5.024,
所以能在犯错概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关.
(Ⅱ)由(Ⅰ)可知“支持”的企业中,中小企业家数之比为1:3,
按分层抽样得到的12家中,中小企业分别为3家和9家.
设9家获得奖励的企业中,中小企业分别为m家和n家,则(m,n)可能为
(0,9),(1,8),(2,7),(3,6).与之对应,
X的可能取值为90,130,170,210.
P(X=90)==, P(X=130)==,
P(X=170)==, P(X=210)==,
分布列如下:
X 90 130 170 210
P
期望E(X)=90×+130×+170×+210×=180。
55. 解: (Ⅰ)取中点,连结,依题意可知△,△均为正三角形,
所以,,又,平面,平面,
所以平面,又平面,所以,
因为,所以。
(Ⅱ)由(Ⅰ)可知,又平面平面,
平面平面,
平面,所以平面.
以为原点,建立空间直角坐标系如图所示,则
,,,,
由可得点的坐标为,
所以,,
设平面的法向量为,则,即
解得,令,得,
显然平面的一个法向量为,
依题意,解得或(舍去),
所以,当时,二面角的余弦值为.
56. 解:(I)证明:由题设知,三棱柱的侧面为矩形.
由于D为AA1的中点,故DC=DC1.
又,可得DC12+DC2=CC12,
所以DC1⊥DC.而DC1⊥BD,DC∩BD=D,所以DC1⊥平面BCD.
BC平面BCD,故DC1⊥BC.
(II)由(I)知BC⊥DC1,且BC⊥CC1,
则BC⊥平面ACC1,所以CA,CB,CC1两两相互垂直.
以C为坐标原点,的方向为x轴的正方向, 为单位长,建立如图所示的空间直角坐标系C-xyz.由题意知A1(1,0,2),B(0,1,0),D(1,0,1),C1(0,0,2).
则,,,
设是平面A1B1BD的法向量,
则,即,可取n=(1,1,0).
同理,设m是平面C1BD的法向量,
可取m=(1,2,1).
.
故二面角A1-BD-C1的大小为30°
57. 解:(I)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,
俯视图为直角梯形,∴两两垂直。
且 ,
以BA,BB1 ,BC分别为轴建立空间直角坐标系,如图
则N(4,4,0),B1(0, 8,0),C1(0,8,4),C(0,0,4)
∵=(4,4,0)·(-4,4,0)=-16+16=0
=(4,4,0)·(0,0,4)=0
∴BN⊥NB1,BN⊥B1C1且NB1与B1C1相交于B1,
∴BN⊥平面C1B1N;
(II)设为平面的一个法向量,
则
则
(Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,
则, ∵MP//平面CNB1,
∴
又,
∴当PB=1时MP//平面CNB1
58. 解:(I)由题: ①
左焦点 (-c,0) 到点 P(2,1) 的距离为:
d = =②
由①②可解得c = 1, a = 2 , b 2 = a 2-c 2 = 3.
∴所求椭圆 C 的方程为 .
(II)设 A(x1,y1)、B(x2,y2),将 y = kx + m代入椭圆方程得
(4k 2 + 3) x 2 + 8kmx + 4m 2-12 = 0.
∴x1 + x2 = -,x1x2 = ,且y1 = kx1 + m,y2 = kx2 + m.
∵AB为直径的圆过椭圆右顶点 A2(2,0) ,所以 = 0.
所以 (x1-2,y1)·(x2-2, ( http: / / www.21cnjy.com )y2) = (x1-2) (x2-2) + y1y2 = (x1-2) (x2-2) + (kx1 + m) (kx2 + m)21世纪教育网版权所有
= (k 2 + 1) x1x2 + (km-2) (x1 + x2) + m 2 + 4
= (k 2 + 1)·-(km-2)·+ m 2 + 4 = 0 .
整理得 7m 2 + 16km + 4k 2 = 0.∴m = -k 或 m = -2k 都满足 △ > 0.
若 m = -2k 时,直线 l 为 y = kx-2k = k (x-2) ,恒过定点 A2(2,0),不合题意舍去;21·世纪*教育网
若 m = -k 时,直线 l 为 y = kx-k = k (x-), 恒过定点 (,0) .
59. 解:(I)由使得的点P恰有两个可得;动点P到焦点的距离的最大值为,可得,即,所以椭圆的方程是 【出处:21教育名师】
(II)圆的方程为,设直线上动点T的坐标为设,,则直线AT的方程为,直线BT的方程为,又在直线AT和BT上,即,故直线AB的方程为 21教育名师原创作品
由原点O到直线AB的距离得,
联立,消去x得,设,。
则, 从而
所以,设,
则,又设,
所以,设,
所以由得:,所以在上单调递增即
60. 解: (Ⅰ)
(Ⅱ)设,则,直线的方程为:
由消元整理可得:
所以 可求得:
直线的方程为: 所以可求得
所以===4.
的中点 ,则的中垂线方程为:
与BC的中垂线轴交点为: 所以的外接圆的方程为:
由上可知
所以四点共圆.
61. 解: (Ⅰ)函数的定义域为,
令 得,
①当时, ,
与的变化情况如下表
0
0 0
减 增 减
所以的单调递减区间是,;
②当时, ,,
故的单调递减区间是 ;
③当时, ,
与的变化情况如下表
0
0 0
减 增 减
所以的单调递增减区间是, .
综上,当时,的单调递增减区间是, ;
当时,的单调递增减区间是, ;
当时,的单调递增减区间是.
(Ⅱ)由(Ⅰ)可知
① 当时,在的最大值是
但,所以不合题意;
② 当时,在上单调递减,
,可得在上的最大值为,符合题意.
在上的最大值为0时,的取值范围是。
62. 解:(I)由题意, 由得.
当时, ;当时,.
∴在单调递减,在单调递增
即在处取得极小值,且为最小值,
其最小值为
(II)对任意的恒成立,即在上,.
由(I),设,所以.
由得.
易知在区间上单调递增,在区间上单调递减,
∴在处取得最大值,而.
因此的解为,∴
(III)由(II)得,即,当且仅当时,等号成立,令则,即,
所以
累加得
63. 解:(Ⅰ)当时,定义域,
,又
在处的切线方程
(Ⅱ)①令,则
即
令, 则
令,,
,在上是减函数
又,所以当时,,当时,,
所以在上单调递增,在上单调递减,
,所以当函数有且今有一个零点时,
(Ⅱ)当,,若只需证明
令得或,又,
函数在上单调递增,在上单调递减,在上单调递增
又g()=-e-3+2,g(e)=2e2-3e
∵g()=-e-3+2<2<2e<2e()=g(e),
∴g()<g(e),∴m≥2e2-3ewww-2-1-cnjy-com
64. A.选修4-1:几何证明选讲
解:(I)连接是圆的两条切线, ,
,又为圆的直径,,
,,即得证,
(II),,△∽△,
。
B.选修4-4:坐标系与参数方程
解:(I)圆的参数方程为(为参数)
所以普通方程为
圆的极坐标方程:
(II)点到直线:的距离为 △的面积
所以△面积的最大值为
C.选修4-5:不等式选讲
解:(Ⅰ)因为,所以等价于
由有解,得,且其解集为
又的解集为,故
(Ⅱ)由(Ⅰ)知
又是正实数,
由均值不等式得
当且仅当时取等号。
也即
65. A.选修4-1:几何证明选讲
解:(I)连结OC,∴∠OAC=∠OCA,又∵CA是∠BAF的角平分线,
∴∠OAC=∠FAC,
∴∠FAC=∠ACO,∴OC∥AD.
∵CD⊥AF,
∴CD⊥OC,即DC是⊙O的切线.
(Ⅱ)连结BC,在Rt△ACB中,
CM⊥AB,∴CM2=AM·MB.
又∵DC是⊙O的切线,∴DC2=DF·DA.
易知△AMC≌△ADC,∴DC=CM,
∴AM·MB=DF·DA
B.选修4-4:坐标系与参数方程
解:(Ⅰ)由,得,即曲线的直角坐标方程为.
(Ⅱ)将直线的方程代入,并整理得,,.
所以.
C.选修4-5:不等式选讲
解:(Ⅰ)当时,
由得
当时,不等式可化为即,其解集为
当时,不等式化为,不可能成立,其解集为;
当时,不等式化为,其解集为
综上所述,的解集为
(Ⅱ),∴要成立,
则,,
即的取值范围是。
66.A. 选修4—1:几何证明选讲
解:如图,延长DC,AB交于点E,
则,解得
EMBED Equation.DSMT4
B.选修4—4:坐标系与参数方程
解:(I) 由得即;
由(为参数),消去参数,得;
曲线的直角坐标方程为;直线的普通方程;
(II) 设直线交曲线于,则
,消去得,,,;
所以,直线被曲线截得的线段的长为.
C.选修4—5:不等式选讲
解:(1)
当且仅当时有最小值
(2)证明:证法一:因为由柯西不等式可得:
当且仅当,即时取得等号。
证法二:因为a,b∈R+,a+b=1,,∈R+ 所以
当且仅当时,取得等号。
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
P
A
B
C
D
M
O
x
y
z
F2
O
x
y
P
A
B
F1
A2
l
O
x
y
P
A
B
F1
F2
A2
l
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2015年高考押题 精粹
数学理科
本卷共60题,三种题型:选择题、填空题和解答题。选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)
1. 已知全集, 集合, , 则集合可以表示为( )
A. B. C. D.
2. 集合 ,则集合C中的元素个数为( )
A.3 B.4 C.11 D.12
3. 设集合,,则=( )
A. B. C. D.
4. 若(其中为虚数单位),则等于( )
A.1 B. C. D.
5. 若复数(为虚数单位)是纯虚数,则实数的值为( )
A. B. C. D.
6. 复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7. 已知向量,若,则( )
A. B. C. D.
8. 已知为的边的中点,所在平面内有一个点,满足,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
9.中,,AB=2,AC=1,D是边BC上的一点(包括端点),则 的取值范围是( )
A. [1,2] B.[0,1] C.[0,2] D. [﹣5,2]
10.已知命题:,,命题:,,则下列说法中正确的是( )
A.命题是假命题 B.命题是真命题
C.命题是真命题 D.命题是假命题
11.命题“,”的否定是( )
A., B.,
C., D.,
12.命题:关于的方程有三个实数根;命题:;则命题成立时命题成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
13.若某几何体的三视图如右图所示,则此几何体的体积等于( )
A. B. C. D.
14.某几何体的三视图如图所示,图中三个正方形的边长均为2,则该几何体的体积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
15.某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
( http: / / www.21cnjy.com )
16.已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
17.已知,若的最小值是,则( )
A.1 B.2 C.3 D.4www.21-cn-jy.com
18.已知不等式组构成平面区域(其中,是变量)。若目标函数的最小值为-6,则实数的值为( )【来源:21·世纪·教育·网】
A. B.6 C.3 D.
19. 如图给出的是计算的值的程序框图,其中判断框内应填入的是( )
( http: / / www.21cnjy.com )
A. B. C. D.
20.执行如图所示的程序框图,则输出的结果是( )
A. 14 B. 15 C. 16 D. 17
21. 执行如图所示的程序框图,若输入的值为,则输出的的值为( )
A. B. C. D.
( http: / / www.21cnjy.com )
22. 已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
23. 如图是2013年某大学自主招生面 ( http: / / www.21cnjy.com )试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
A.85,84 B.84,85 C.86,84 D.84,86
( http: / / www.21cnjy.com )
24. 学校为了解学生在课外读物方面的支出情况,抽取了个同学进行调查,结果显示这些同学的支出都在(单 位:元),其中支出在(单位:元)的同学有67人,其频率分布直方图如图所示,则的值为( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.100 B.120 C.130 D.390
25. 若,是第三象限的角,则( )
A. B. C. D.
26. 在中,若的形状一定是( )
A.等边三角形 B.不含的等腰三角形 C.钝角三角形 D.直角三角形
27. 已知,函数在上单调递减,则的取值范围是( )
A. B. C. D.
28. 函数的最小正周期为,为了得到的图象,只需将函数的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
29. 在中,是边上的一点,,的面积为,则的长为( )
A. B. C. D.
30. 已知函数的最小正周期为,最小值为,将函数的图像向左平移(>0)个单位后,得到的函数图形的一条对称轴为,则的值不可能为( )
A. B. C. D.
31. 已知双曲线的离心率为,则的值为( )
A. B. C. D.
32. 如图过拋物线的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )
A. B
C. D.[]
33. 椭圆M: 左右焦点分别为,,P为椭圆M上任一点且 最大值取值范围是,其中,则椭圆离心率e取值范围为 ( )【版权所有:21教育】
A. B. C. D.
34. 已知函数,则函数的大致图像为( ) ( http: / / www.21cnjy.com )
35. 已知函数,则关于的方程的实根个数不可能为( )
A.个 B.个 C.个 D.个
36. 设定义在D上的函数在点处的切线方程为,当时,若在D内恒成立,则称P为函数的“类对称点”,则的“类对称点”的横坐标是( )
A.1 B. C.e D.
二、填空题(12个小题)
37. 二项式的展开式中的常数项是________.
38. 有4名优秀学生,,,全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有 种.
39.设,则二项式展开式中含项的系数是_____
40. 如图,设是图中边长为4的正方形区域,是内函数图象下方的点构成的区域.在内随机取一点,则该点落在中的概率为 。
( http: / / www.21cnjy.com )
41. 随机向边长为5,5,6的三角形中投一点P,则点P到三个顶点的距离都不小于1的概率是 。
42. 一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当有两个数
字的和等于第三个数字时称为“有缘数”(如213,134等),若,且a,
b,c互不相同,则这个三位数为”有缘数”的概率是_________。
43. 是同一球面上的四个点,其中是正三角形, ⊥平面,,则该球的表面积为_________。
44. 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥. 如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该半球的体积为 。
( http: / / www.21cnjy.com )
45. 已知四棱锥中,底面为矩形,且中心为,,,则该四棱锥的外接球的体积为 。
46. 已知等差数列前项和为,且满足,则数列的公差为 。
47.已知为数列的前项和,且满足,,则 。
48. 已知数列的前n项和,若不等式对恒成立,则整数的最大值为 。
三、解答题(18个小题)
49. 在中,内角的对边分别为已知.
(I)求的值; (II)若,,求的面积。
50. 在△ABC中,a,b,c是其三个内角A,B,C的对边,且.
(Ⅰ)求角C的大小;
(Ⅱ)设,求△ABC的面积S的最大值。
51. 已知数列中,,其前项的和为,且满足.
(Ⅰ) 求证:数列是等差数列;(Ⅱ) 证明:当时,.
52. 第117届中国进出品商品交易会(简 ( http: / / www.21cnjy.com )称2015年春季广交会)将于2015年4月15日在广州举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:cm),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”。
( http: / / www.21cnjy.com )
(Ⅰ)计算男志愿者的平均身高和女志愿者身高的中位数(保留一位小数)。
(Ⅱ)若从所有“高个子”中选3名志愿者,用表示所选志愿者中为女志愿者的人数,试写出的分布列,并求的数学期望。【来源:21cnj*y.co*m】
53. 某学校从参加2015年迎新百科知识 ( http: / / www.21cnjy.com )竞赛的同学中,选取40名同学,将他们的成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题。
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)从频率分布直方图中,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
( http: / / www.21cnjy.com )
54. 某市工业部门计划度所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行问卷调查,结果如下表:21教育网
支持 不支持 合计
中型企业 80 40 120
小型企业 240 200 440
合计 320 240 560
(Ⅰ)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?21cnjy.com
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出12家,然后从这12家中选出9家进行奖励,分别奖励中、小企业每家50万元、10万元。记表示所发奖励的钱数,求的分布列和数学期望:
附:
0.050 0.025 0.010
3.841 5.024 6.635
55.如图,四棱锥,侧面是边长为的正三角形,且与底面垂直,底面是的菱形,为棱上的动点,且()。
(Ⅰ) 求证:;(Ⅱ) 试确定的值,使得二面角的平面角余弦值为。
( http: / / www.21cnjy.com )
56. 如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD.
( http: / / www.21cnjy.com )
(I)证明:DC1⊥BC;
(II)求二面角A1-BD-C1的大小.
57. 已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(I)求证:平面;
(II)设为直线与平面所成的角,求的值;
(Ⅲ)设为中点,在边上求一点,使平面,求的值.
58. 椭圆的离心率为,其左焦点到点的距离为.
(I)求椭圆的标准方程;
(II) 若直线与椭圆相交于两点(不是左右顶点),且以为直径的圆过椭圆的右顶点,求证:直线过定点,并求出该定点的坐标.
59. 已知椭圆 的两个焦点,,动点P在椭圆上,且使得的点P恰有两个,动点P到焦点的距离的最大值为。
(I)求椭圆的方程;
(II)如图,以椭圆的长轴为直径作圆,过直线上的动点T作圆的两条切线,设切点分别为A,B,若直线AB与椭圆交于不同的两点C,D,求的取值范围。 ( http: / / www.21cnjy.com )
60. 已知抛物线的焦点到准线的距离为2。
(Ⅰ)求的值;
(Ⅱ)如图所示,直线与抛物线相交于,两点,为抛物线上异于,的一点,且轴,过作的垂线,垂足为,过作直线交直线BM于点,设的斜率分别为,且。
① 线段的长是否为定值 若是定值,请求出定值;若不是定值,请说明理由;
② 求证:四点共圆.
( http: / / www.21cnjy.com )
61. 已知,其中.
(Ⅰ)求的单调递减区间;
(Ⅱ)若在上的最大值是,求的取值范围.
62. 已知函数为自然对数的底数)
(I)求函数的最小值;
(II)若≥0对任意的∈R恒成立,求实数a的值;
(III)在(II)的条件下,证明:
63. 已知函数.
(Ⅰ)当时,求在处的切线方程;
(Ⅱ)设函数,
①若函数有且仅有一个零点时,求的值;
②在①的条件下,若,,求的取值范围。
64. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
A.选修4-1:几何证明选讲
如图所示,为圆的直径,,为
圆的切线,,为切点.
(Ⅰ)求证: ;
(Ⅱ)若圆的半径为2,求的值.
B.选修4-4:坐标系与参数方程
已知在直角坐标系中,圆的参数方程为(为参数).
(Ⅰ)以原点为极点、轴正半轴为极轴建立极坐标系,求圆的极坐标方程;
(Ⅱ)已知,圆上任意一点,求△面积的最大值.
C.选修4-5:不等式选讲
已知函数且的解集为
(Ⅰ)求k的值;
(Ⅱ)若是正实数,且,求证:。
65. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑
A.选修4—1:几何证明选讲
如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
(I)求证:DC是⊙O的切线;
(II)求证:AM·MB=DF·DA.
B.选修4-4:坐标系与参数方程
极坐标系与直角坐标系有相同的长度单位,以原点为极点,以轴正半轴为极轴.已知直线的参数方程为(为参数),曲线的极坐标方程为.
(I)求的直角坐标方程;
(II)设直线与曲线交于两点,求弦长.
C.选修4-5:不等式选讲
已知函数
(I)若,解不等式;
(II)如果,求的取值范围.
66. 请考生在A,B,C三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑
A. 选修4—1:几何证明选讲
如图,四边形ABCD内接于圆.
求对角线BD、AC的长.
B.选修4—4:坐标系与参数方程
已知曲线的极坐标方程为,以极点为坐标原点,极轴为轴正半轴建立
平面直角坐标系,直线的参数方程为(为参数)
(I)把曲线的极坐标方程化为直角坐标方程,把直线的参数方程化为普通方程;
(II)求直线被曲线截得的线段的长.
C.选修4—5:不等式选讲
已知a,b∈,a+b=1,,∈.
(1)求的最小值;
(2)求证:.
参考答案
一、选择题(36个小题)
1.答案:B
解析:有元素1,2的是,分析选项则只有B符合。
2. 答案:C
解析:,故选C。
3. 答案:C
解析:集合,。
4. 答案:C
解析:化简得,则=,故选C。
5. 答案:A
解析:,所以。
6. 答案:D
解析:根据复数的运算可知,所以复数的坐标为,所以正确选项为D。
7. 答案:B
解析:,
。
8. 答案:C
解析:如图,四边形是平行四边形,D为边BC的中点,所以D为边的中点,的值为1。
9. 答案:D
解析:∵D是边BC上的一点(包括端点),
∴可设
,,,
的取值范围是。
10. 答案:C
解析:命题为真命题.对命题,当时,,故为假命题,为真命题.所以C正确。
11. 答案:C
解析:命题“,” 是特称命题,则它的否定是全称命题,即。
12. 答案:B
解析:由方程,易知函数是上的奇函数,由的图像可知,函数在上的最大值是1,根据图像的对称性知函数在上的最小值为-1,又函数的图像与轴有3个交点,那么原方程有3个实数根的充要条件是,而,所以选择B。21*cnjy*com
13. 答案:C
解析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,
如图,故选。
14. 答案:D
解析:由三视图可知此几何体是:棱长为2 的正方体挖去了一个圆锥而形成的新几何体,其体积为,故选 D。
15. 答案:A
解析:该几何体是下面是一个三棱柱,上面是一个有一个侧面垂直于底面的三棱锥。其体积为。
16. 答案:B
解析:依题意可以画出不等式表示的图形,当过点时取最小值,即2-2=1,=。
17. 答案:B
解析:由已知得线性可行域如图所示,则的最小值为,若,则为最小值最优解,∴,若,则为最小值最优解,不合题意,故选B。
( http: / / www.21cnjy.com )
18. 答案:C
解析:不等式组表示的平面区域如图阴影部分所示,因为,故。可知在C点处取得最小值,联立解得即,故,解得。
( http: / / www.21cnjy.com )
19. 答案:B
解析:由程序知道,都应该满足条件,不满足条件,故应该选择B。
20. 答案:C
解析:由程序框图可知,从到得到,因此将输出
. 故选C。
21. 答案:B
解析:第一次运行时,;第二次运行时,;
第三次运行时,;第四次运行时,;
第五次运行时,;…,以此类推,
直到,程序才刚好不满足,故输出.故选B。
22. 答案:C
解析:将代入回归方程为可得,则,解得,即精确到0.1后的值为. 故选C。
23. 答案:A
解析:去掉一个最高分和一个最低分后,所剩数据为84,84,86,84,87,平均数为,众数为84. 故选A。
24. 答案:A
解析:支出在的同学的频率为,。
25. 答案:B
解析:由题意,因为是第三象限的角,所以,
因此。
26. 答案:D
解析:∵sin(A-B)= ( http: / / www.21cnjy.com )1+2cos(B+C)sin(A+C),∴sin(A-B)=1-2cosAsinB,
∴sinAcosB-cosAsinB=1-2cosAsinB,∴sinAcosB+cosAsinB=1,
∴sin(A+B)=1,∴A+B=90°,∴△ABC是直角三角形。
27. 答案:A
解析:结合特殊值,求解三角函数的递减区间,并验证结果.取,,其减区间为,显然,排除;取,,其减区间为,显然,排除.选。
28. 答案:C
解析:因为函数的最小正周期为,所以,则,则用换x即可得到的图像,所以向左平移个单位长度,则选C。
29. 答案:D
解析:因为,可得,即,所以.在中,由余弦定理,解得,所以,所以,
在中,由正弦定理可知,可得。
30. 答案:B
解析:,依题意,,所以,因为,解得,故,故,所以,即。将函数的图片向左平移(>0)个单位后得到,因为函数的一条对称轴为。故,解得,观察可知,选B。 21*cnjy*com
31. 答案:B
解析:依题意,,。
32. 答案:D
解析:如图分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则由已知得:|BC|=2a,由定义得:|BD|=a,故∠BCD=30°,
在直角三角形ACE中,∵|AF|=3,|AC|=3+3a,∴2|AE|=|AC|
∴3+3a=6,从而得a=1,∵BD∥FG,∴,求得p=,因此抛物线方程为y2=3x。
33. 答案:B
解析:由椭圆定义知,
的最大值为
而最大值取值范围是,所以
于是得到,
故椭圆的离心率的取值范围是,选B。
34. 答案:A
解析:由函数的奇偶性可知函数为非奇非偶函数,所以排除B,C,再令,说明当x为负值时,有小于零的函数值,所以排除D。
35. 答案:A
解析:因为时,=1或=3或=或=-4,则当a=1时或1或3或-4,又因为,则当时只有一个
=-2与之对应其它情况都有两个值与之对应,所以此时所求方程有7个根,当1<a<2时因为函数与y=a有4个交点,每个交点对应两个,则此时所求方程有8个解,当a=2时函数与y=a有3个交点,每个交点对应两个,则此时所求方程有6个解,所以B,C,D都有可能,则选A。
36. 答案:B
解析:由于,则在点P处切线的斜率.
所以切线方程为
,
则,.
当时,在上单调递减,所以当时, 从而有时,;
当时,在上单调递减,所以当时, 从而有时,;
所以在上不存在“类对称点”. 当时,,所以在上是增函数,故
所以是一个类对称点的横坐标. (可以利用二阶导函数为0,求出,则。
二、填空题(12个小题)
37. 答案:45
解析:,则,故常数项为。
38. 答案:36
解析:先从4名优秀学生,,,中选出2名保送到甲,乙,丙3所学校中的某一所,有种方案;然后将剩余的2名优秀学生保送到剩余的2所学校,有种方案;故不同的保送方案共有种。
39. 答案:-192
解析:由于
则含项的系数为。
40. 答案:
解析:由几何概型得,该点落在中的概率为。
41. 答案:
解析:分别以三角形的三个顶点为圆心,1为半径作圆,则在三角形内部且在三圆外部的区域即为与三角形三个顶点距离不小于1的部分,即。
42. 答案:
解析:由1,2,3组成的三位自然数为123,132,213,231,312,321,共6个;
同理由1,2,4组成的三位自然数共6个;
由1,3,4组成的三位自然数也是6个;
由2,3,4组成的三位自然数也是6个.
所以共有6+6+6+6=24个.
由1,2,3组成的三位自然数,共6个”有缘数”.
由1,3,4组成的三位自然数,共6个”有缘数”.
所以三位数为”有缘数”的概率。
43. 答案:32
解析:由题意画出几何体的图形如图,
把A、B、C、D扩展为三棱柱,上下底面中心连线的中点与A的距离为球的半径,
AD=4,AB=2,△ABC是正三角形,所以AE=2,AO=2。
所求球的表面积为:4(2)2=32。
( http: / / www.21cnjy.com )
44. 答案:
解析:设所给半球的半径为,则棱锥的高,底面正方形中有,所以其体积,则,
于是所求半球的体积为。
45. 答案:
解析:因为,故,故;同理,;将四棱锥补成一个长方体,可知该长方体的长宽高分别为,故所求外接球的半径,其体积。
46. 答案:2
解析:∵,∴,∴,又,∴。
47. 答案:2×31007﹣2
解析:由anan+1=3n,得,
∴,
则数列{an}的所有奇数项和偶数项均构成以3为公比的等比数列,
又.
∴。
48. 答案:4
解析:当时,得,;
当时,,两式相减得,得,
所以。
又,所以数列是以2为首项,1为公差的等差数列,,即。
因为,所以不等式,等价于。
记,时,。
所以时,。
所以,所以整数的最大值为4。
三、解答题(18个小题)
49. 解:(Ⅰ)由正弦定理,得
所以
即,
化简得,即因此
(Ⅱ)由的
由及
得,解得,因此
又所以,因此
50. 解:(Ⅰ)∵
,或,
由,知,所以不可能成立,所以,
即,
所以
(Ⅱ)由(Ⅰ),,所以,
即△ABC的面积S的最大值为
51. 解:(Ⅰ)当时,,
,,
从而构成以1为首项,2为公差的等差数列.
(Ⅱ)由(1)可知,,.
当时,.
从而。
52. 解:(1)根据茎叶图可得:
男志愿者的平均身高为
女志愿者身高的中位数为
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,而男志愿者的“高个子”有5人,女志愿者的“高个子”有3人2-1-c-n-j-y
的可能值为0,1,2,3,
故
即的分布列为:
0 1 2 3
P
所以的数学期望
53. 解:(Ⅰ)设分数在内的频率为,根据频率分布直方图,
则有,
可得,所以频率分布直方图如图所示.
( http: / / www.21cnjy.com )
(Ⅱ)平均分:
(Ⅲ)学生成绩在的有人,
在的有人,并且的可能取值是0,1,2。
,;
。
所以的分布列为
0 1 2
21·cn·jy·com
所以。
54. 解:(Ⅰ)K2=≈5.657,因为5.657>5.024,
所以能在犯错概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关.
(Ⅱ)由(Ⅰ)可知“支持”的企业中,中小企业家数之比为1:3,
按分层抽样得到的12家中,中小企业分别为3家和9家.
设9家获得奖励的企业中,中小企业分别为m家和n家,则(m,n)可能为
(0,9),(1,8),(2,7),(3,6).与之对应,
X的可能取值为90,130,170,210.
P(X=90)==, P(X=130)==,
P(X=170)==, P(X=210)==,
分布列如下:
X 90 130 170 210
P
期望E(X)=90×+130×+170×+210×=180。
55. 解: (Ⅰ)取中点,连结,依题意可知△,△均为正三角形,
所以,,又,平面,平面,
所以平面,又平面,所以,
因为,所以。
(Ⅱ)由(Ⅰ)可知,又平面平面,
平面平面,
平面,所以平面.
以为原点,建立空间直角坐标系如图所示,则
,,,,
由可得点的坐标为,
所以,,
设平面的法向量为,则,即
解得,令,得,
显然平面的一个法向量为,
依题意,解得或(舍去),
所以,当时,二面角的余弦值为.
56. 解:(I)证明:由题设知,三棱柱的侧面为矩形.
由于D为AA1的中点,故DC=DC1.
又,可得DC12+DC2=CC12,
所以DC1⊥DC.而DC1⊥BD,DC∩BD=D,所以DC1⊥平面BCD.
BC平面BCD,故DC1⊥BC.
(II)由(I)知BC⊥DC1,且BC⊥CC1,
则BC⊥平面ACC1,所以CA,CB,CC1两两相互垂直.
以C为坐标原点,的方向为x轴的正方向, 为单位长,建立如图所示的空间直角坐标系C-xyz.由题意知A1(1,0,2),B(0,1,0),D(1,0,1),C1(0,0,2).
则,,,
设是平面A1B1BD的法向量,
则,即,可取n=(1,1,0).
同理,设m是平面C1BD的法向量,
可取m=(1,2,1).
.
故二面角A1-BD-C1的大小为30°
57. 解:(I)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,
俯视图为直角梯形,∴两两垂直。
且 ,
以BA,BB1 ,BC分别为轴建立空间直角坐标系,如图
则N(4,4,0),B1(0, 8,0),C1(0,8,4),C(0,0,4)
∵=(4,4,0)·(-4,4,0)=-16+16=0
=(4,4,0)·(0,0,4)=0
∴BN⊥NB1,BN⊥B1C1且NB1与B1C1相交于B1,
∴BN⊥平面C1B1N;
(II)设为平面的一个法向量,
则
则
(Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,
则, ∵MP//平面CNB1,
∴
又,
∴当PB=1时MP//平面CNB1
58. 解:(I)由题: ①
左焦点 (-c,0) 到点 P(2,1) 的距离为:
d = =②
由①②可解得c = 1, a = 2 , b 2 = a 2-c 2 = 3.
∴所求椭圆 C 的方程为 .
(II)设 A(x1,y1)、B(x2,y2),将 y = kx + m代入椭圆方程得
(4k 2 + 3) x 2 + 8kmx + 4m 2-12 = 0.
∴x1 + x2 = -,x1x2 = ,且y1 = kx1 + m,y2 = kx2 + m.
∵AB为直径的圆过椭圆右顶点 A2(2,0) ,所以 = 0.
所以 (x1-2,y1)·(x2-2, ( http: / / www.21cnjy.com )y2) = (x1-2) (x2-2) + y1y2 = (x1-2) (x2-2) + (kx1 + m) (kx2 + m)21世纪教育网版权所有
= (k 2 + 1) x1x2 + (km-2) (x1 + x2) + m 2 + 4
= (k 2 + 1)·-(km-2)·+ m 2 + 4 = 0 .
整理得 7m 2 + 16km + 4k 2 = 0.∴m = -k 或 m = -2k 都满足 △ > 0.
若 m = -2k 时,直线 l 为 y = kx-2k = k (x-2) ,恒过定点 A2(2,0),不合题意舍去;21·世纪*教育网
若 m = -k 时,直线 l 为 y = kx-k = k (x-), 恒过定点 (,0) .
59. 解:(I)由使得的点P恰有两个可得;动点P到焦点的距离的最大值为,可得,即,所以椭圆的方程是 【出处:21教育名师】
(II)圆的方程为,设直线上动点T的坐标为设,,则直线AT的方程为,直线BT的方程为,又在直线AT和BT上,即,故直线AB的方程为 21教育名师原创作品
由原点O到直线AB的距离得,
联立,消去x得,设,。
则, 从而
所以,设,
则,又设,
所以,设,
所以由得:,所以在上单调递增即
60. 解: (Ⅰ)
(Ⅱ)设,则,直线的方程为:
由消元整理可得:
所以 可求得:
直线的方程为: 所以可求得
所以===4.
的中点 ,则的中垂线方程为:
与BC的中垂线轴交点为: 所以的外接圆的方程为:
由上可知
所以四点共圆.
61. 解: (Ⅰ)函数的定义域为,
令 得,
①当时, ,
与的变化情况如下表
0
0 0
减 增 减
所以的单调递减区间是,;
②当时, ,,
故的单调递减区间是 ;
③当时, ,
与的变化情况如下表
0
0 0
减 增 减
所以的单调递增减区间是, .
综上,当时,的单调递增减区间是, ;
当时,的单调递增减区间是, ;
当时,的单调递增减区间是.
(Ⅱ)由(Ⅰ)可知
① 当时,在的最大值是
但,所以不合题意;
② 当时,在上单调递减,
,可得在上的最大值为,符合题意.
在上的最大值为0时,的取值范围是。
62. 解:(I)由题意, 由得.
当时, ;当时,.
∴在单调递减,在单调递增
即在处取得极小值,且为最小值,
其最小值为
(II)对任意的恒成立,即在上,.
由(I),设,所以.
由得.
易知在区间上单调递增,在区间上单调递减,
∴在处取得最大值,而.
因此的解为,∴
(III)由(II)得,即,当且仅当时,等号成立,令则,即,
所以
累加得
63. 解:(Ⅰ)当时,定义域,
,又
在处的切线方程
(Ⅱ)①令,则
即
令, 则
令,,
,在上是减函数
又,所以当时,,当时,,
所以在上单调递增,在上单调递减,
,所以当函数有且今有一个零点时,
(Ⅱ)当,,若只需证明
令得或,又,
函数在上单调递增,在上单调递减,在上单调递增
又g()=-e-3+2,g(e)=2e2-3e
∵g()=-e-3+2<2<2e<2e()=g(e),
∴g()<g(e),∴m≥2e2-3ewww-2-1-cnjy-com
64. A.选修4-1:几何证明选讲
解:(I)连接是圆的两条切线, ,
,又为圆的直径,,
,,即得证,
(II),,△∽△,
。
B.选修4-4:坐标系与参数方程
解:(I)圆的参数方程为(为参数)
所以普通方程为
圆的极坐标方程:
(II)点到直线:的距离为 △的面积
所以△面积的最大值为
C.选修4-5:不等式选讲
解:(Ⅰ)因为,所以等价于
由有解,得,且其解集为
又的解集为,故
(Ⅱ)由(Ⅰ)知
又是正实数,
由均值不等式得
当且仅当时取等号。
也即
65. A.选修4-1:几何证明选讲
解:(I)连结OC,∴∠OAC=∠OCA,又∵CA是∠BAF的角平分线,
∴∠OAC=∠FAC,
∴∠FAC=∠ACO,∴OC∥AD.
∵CD⊥AF,
∴CD⊥OC,即DC是⊙O的切线.
(Ⅱ)连结BC,在Rt△ACB中,
CM⊥AB,∴CM2=AM·MB.
又∵DC是⊙O的切线,∴DC2=DF·DA.
易知△AMC≌△ADC,∴DC=CM,
∴AM·MB=DF·DA
B.选修4-4:坐标系与参数方程
解:(Ⅰ)由,得,即曲线的直角坐标方程为.
(Ⅱ)将直线的方程代入,并整理得,,.
所以.
C.选修4-5:不等式选讲
解:(Ⅰ)当时,
由得
当时,不等式可化为即,其解集为
当时,不等式化为,不可能成立,其解集为;
当时,不等式化为,其解集为
综上所述,的解集为
(Ⅱ),∴要成立,
则,,
即的取值范围是。
66.A. 选修4—1:几何证明选讲
解:如图,延长DC,AB交于点E,
则,解得
EMBED Equation.DSMT4
B.选修4—4:坐标系与参数方程
解:(I) 由得即;
由(为参数),消去参数,得;
曲线的直角坐标方程为;直线的普通方程;
(II) 设直线交曲线于,则
,消去得,,,;
所以,直线被曲线截得的线段的长为.
C.选修4—5:不等式选讲
解:(1)
当且仅当时有最小值
(2)证明:证法一:因为由柯西不等式可得:
当且仅当,即时取得等号。
证法二:因为a,b∈R+,a+b=1,,∈R+ 所以
当且仅当时,取得等号。
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
P
A
B
C
D
M
O
x
y
z
F2
O
x
y
P
A
B
F1
A2
l
O
x
y
P
A
B
F1
F2
A2
l
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
