3.5 探索与表达规律 课件(共33张PPT) 北师大版 数学八年级上学期
文档属性
| 名称 | 3.5 探索与表达规律 课件(共33张PPT) 北师大版 数学八年级上学期 |  | |
| 格式 | pptx | ||
| 文件大小 | 762.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 12:36:14 | ||
图片预览








文档简介
(共33张PPT)
北师版 八上
3. 5 探索与表达规律
数式中的规律
(1)请找出同一横行上三个相邻数、竖列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系: 相差1.
竖列上三个相邻数的关系: 相差7.
(2)请同学们找一找右上左下、左上右下对角线上三个相邻数的关系.
左上右下对角线上三个相邻数的关系:下一行比上一行多8.
左下右上对角线上三个相邻数的关系:下一行比上一行多6.
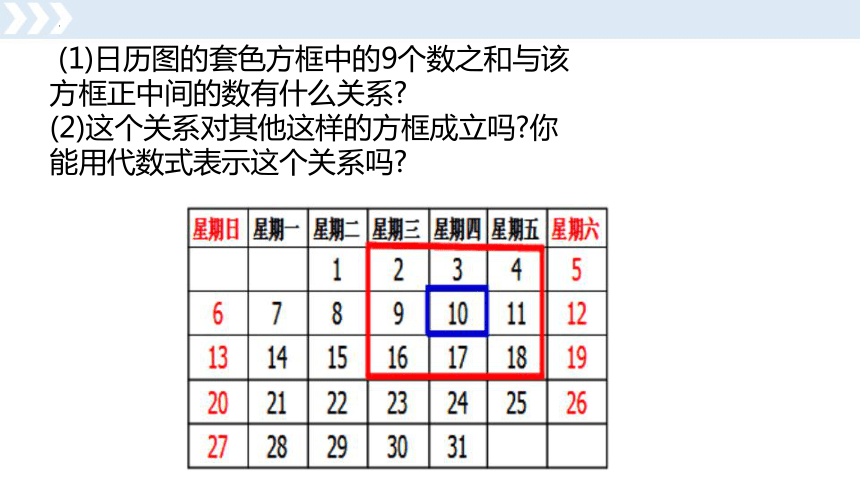
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
(2)这个关系对其他这样的方框成立吗 你能用代数式表示这个关系吗
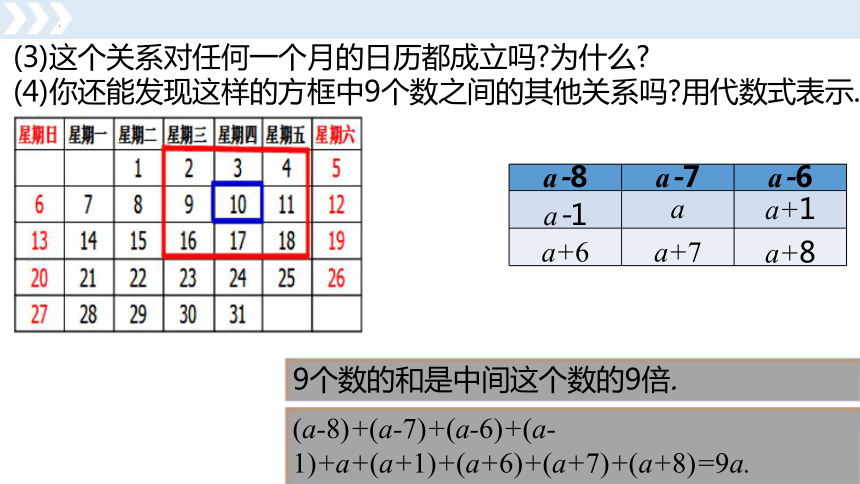
(3)这个关系对任何一个月的日历都成立吗 为什么
(4)你还能发现这样的方框中9个数之间的其他关系吗 用代数式表示.
9个数的和是中间这个数的9倍.
a-8 a-7
a-6
a-1 a
a+1
a+6 a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)=9a.
日历中的其他规律
(1)如果将方框改为十字形框,你能发现哪些规律 如果改为H形框呢
(2)你还能设计其他形状的包含数字规律的数框吗
十字形中的数字有何规律?你是如何验证的?
规律: 十字形中五数之和=5×中间数
规律: “H”形中七数之和=7×中间数
“H”形中的数字有何规律?你是如何验证的?
你还能设计其他形状的包含数字规律的数框吗?
“X”形
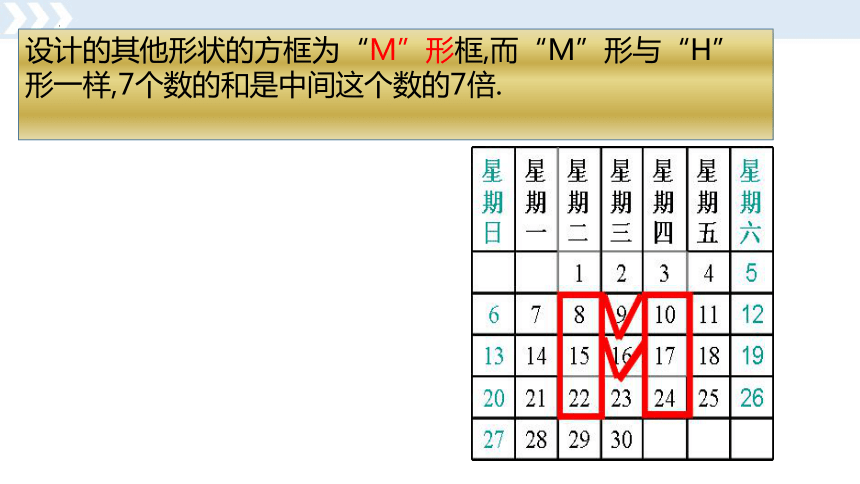
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
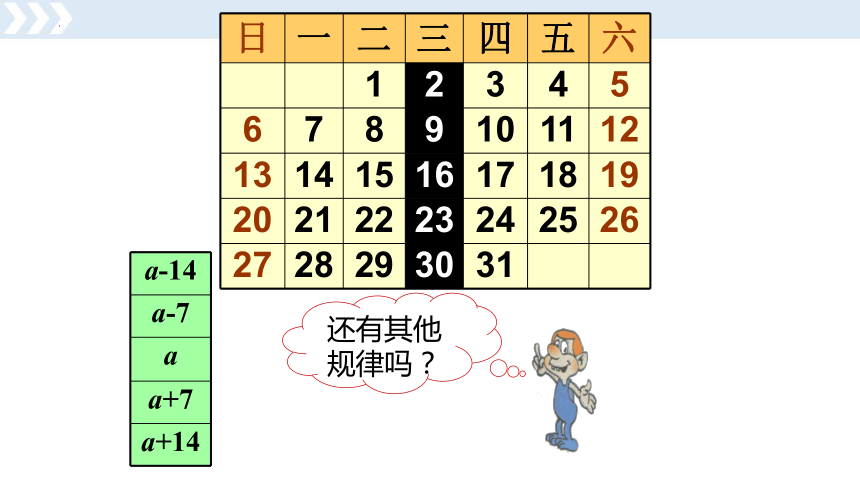
还有其他规律吗?
a-14
a-7
a
a+7
a+14
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+1
a+7 a+8
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+1 a+2 a+3
a+7 a+8 a+9 a+10
a+14 a+15 a+16 a+17
a+21 a+22 a+23 a+24
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+3
a+8 a+9
a+15 a+16
a+21 a+24
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
具 体 问 题
观察、比较
成立
得出结论
不成立
头 回
新 重
索 探
归纳
1.有一串数字 3,6,9,12,15……第n个数字是 .
解析: 3=3×1,
6=3×2,
9=3×3,
12=3×4,
15=3×5……所以第n个数字是3n
3n
4.观察下列等式:
32-12=4×2;
42-22=4×3;
52-32=4×4;
( )2 -( )2=( )×( );
填写第4个等式,第n个等式为_____________________ .
6
4
4
5
议一议
观察下列等式,找出规律填空:
典例精析
方法归纳
用代数式表示数的变化的规律:
(1)数字为整数,相邻两数考虑和、差、积、商、符号、奇、偶、平方等规律;
(2)数字为分数,观察分子、分母的变化及联系;
(3)若是等式(表格),将每个等式对应写好,比较每一行每一列数字之间的关系
C
64x7
(1)按如图方式摆放餐桌和椅子,照这样的方式继续排列餐桌,
摆4张桌子可坐多少人 摆5张桌子呢
摆n张桌子呢
每增加一张桌子多坐2人,
所以4张桌子可以坐12人,
5张桌子可以坐14人,
n张桌子可以坐(2n+4)人.
图形拼接中的规律
二
49
下面是用棋子摆成的“小屋子”
(1)按图示规律填写下表:
图形编号 1 2 3 4 …
n
棋子个数
(2)按这种方式摆下去,摆第n个这样的“小屋子”需要多少枚棋子 你是怎样得到的
6n-1
5,11,17,23……
练一练
观察下列图形,则第n个图形中三角形的个数是( )
A.2n+2 B.4n+4 C.4n-4 D.4n
D
例3 将棱长为1的正方体层层叠放如图所示,
问第(5)个、第(6)个图形各需多少个正方体?
解:
第(5)个图形需1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)=35(个)正方体.
同理,第(6)个图形需56个正方体.
练一练
如图,用灰、白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖有________块.
(3n+2)
第1个图案中白色瓷砖的块数为1+3+1=5,
第2个图案中白色瓷砖的块数为2+4+2=8,
第3个图案中白色瓷砖的块数为3+5+3=11,依此规律可以得到第n个图案中白色瓷砖的块数为5+3(n-1)=3n+2.
2.观察下列球的排列规律(其中●是实心球,○是空心球):
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……
从第1个球起到第2012个球止,共有实心球 个.
解析: 每10个球一循环,
每个循环里有3个实心球,
因:2012÷10=201……2,
所以共有实心球3×201+1=604(个).
604
(2)按如图方式摆放餐桌和椅子,照这样的方式继续排列餐桌,
摆4张桌子可坐多少人
摆5张桌子呢
摆n张桌子呢
序号 1 2 3 4 5 … n
人数 6 10 14 18 22 …
4n+2
3.观察下列图形的排列规律(其中△是三角形,□是正方形,○是圆):
□○△□□○△□○△□□○△□○△□□○△□○△□□……
若第一个图形是正方形,则第2008个图形是 .(填图形名称)
解析:每7个图形一循环,因为2008÷7=286……6,
所以第2008个图形与第6个图形一样
圆
4.用黑白两种颜色的正六边形地砖按
如下所示的规律拼成若干个图案,第(4)
个图案中有黑色地砖4块,那么第(n)个
图案中有白色地砖 块.
……
(4n+2)
解:第1个图案有6块白色瓷砖,
第2个图案有10块白色瓷砖,
每多1块黑色瓷砖则多4块白色瓷砖,
根据此规律可知第n个图案中的白色瓷砖的块数为6+4(n-1),
即4n+2
探索规律的一般步骤
观察特例寻找数量关系
大胆猜想规律
用代数式表示规律
验证规律是否成立
得出结论
成立
不
成
立
课堂小结
数式变化中的规律
图形拼接中的规律
探索与表达规律
探索 猜想 验证
特殊 一般
北师版 八上
3. 5 探索与表达规律
数式中的规律
(1)请找出同一横行上三个相邻数、竖列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系: 相差1.
竖列上三个相邻数的关系: 相差7.
(2)请同学们找一找右上左下、左上右下对角线上三个相邻数的关系.
左上右下对角线上三个相邻数的关系:下一行比上一行多8.
左下右上对角线上三个相邻数的关系:下一行比上一行多6.
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
(2)这个关系对其他这样的方框成立吗 你能用代数式表示这个关系吗
(3)这个关系对任何一个月的日历都成立吗 为什么
(4)你还能发现这样的方框中9个数之间的其他关系吗 用代数式表示.
9个数的和是中间这个数的9倍.
a-8 a-7
a-6
a-1 a
a+1
a+6 a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)=9a.
日历中的其他规律
(1)如果将方框改为十字形框,你能发现哪些规律 如果改为H形框呢
(2)你还能设计其他形状的包含数字规律的数框吗
十字形中的数字有何规律?你是如何验证的?
规律: 十字形中五数之和=5×中间数
规律: “H”形中七数之和=7×中间数
“H”形中的数字有何规律?你是如何验证的?
你还能设计其他形状的包含数字规律的数框吗?
“X”形
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a-14
a-7
a
a+7
a+14
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+1
a+7 a+8
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+1 a+2 a+3
a+7 a+8 a+9 a+10
a+14 a+15 a+16 a+17
a+21 a+22 a+23 a+24
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
还有其他规律吗?
a a+3
a+8 a+9
a+15 a+16
a+21 a+24
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
具 体 问 题
观察、比较
成立
得出结论
不成立
头 回
新 重
索 探
归纳
1.有一串数字 3,6,9,12,15……第n个数字是 .
解析: 3=3×1,
6=3×2,
9=3×3,
12=3×4,
15=3×5……所以第n个数字是3n
3n
4.观察下列等式:
32-12=4×2;
42-22=4×3;
52-32=4×4;
( )2 -( )2=( )×( );
填写第4个等式,第n个等式为_____________________ .
6
4
4
5
议一议
观察下列等式,找出规律填空:
典例精析
方法归纳
用代数式表示数的变化的规律:
(1)数字为整数,相邻两数考虑和、差、积、商、符号、奇、偶、平方等规律;
(2)数字为分数,观察分子、分母的变化及联系;
(3)若是等式(表格),将每个等式对应写好,比较每一行每一列数字之间的关系
C
64x7
(1)按如图方式摆放餐桌和椅子,照这样的方式继续排列餐桌,
摆4张桌子可坐多少人 摆5张桌子呢
摆n张桌子呢
每增加一张桌子多坐2人,
所以4张桌子可以坐12人,
5张桌子可以坐14人,
n张桌子可以坐(2n+4)人.
图形拼接中的规律
二
49
下面是用棋子摆成的“小屋子”
(1)按图示规律填写下表:
图形编号 1 2 3 4 …
n
棋子个数
(2)按这种方式摆下去,摆第n个这样的“小屋子”需要多少枚棋子 你是怎样得到的
6n-1
5,11,17,23……
练一练
观察下列图形,则第n个图形中三角形的个数是( )
A.2n+2 B.4n+4 C.4n-4 D.4n
D
例3 将棱长为1的正方体层层叠放如图所示,
问第(5)个、第(6)个图形各需多少个正方体?
解:
第(5)个图形需1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)=35(个)正方体.
同理,第(6)个图形需56个正方体.
练一练
如图,用灰、白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖有________块.
(3n+2)
第1个图案中白色瓷砖的块数为1+3+1=5,
第2个图案中白色瓷砖的块数为2+4+2=8,
第3个图案中白色瓷砖的块数为3+5+3=11,依此规律可以得到第n个图案中白色瓷砖的块数为5+3(n-1)=3n+2.
2.观察下列球的排列规律(其中●是实心球,○是空心球):
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……
从第1个球起到第2012个球止,共有实心球 个.
解析: 每10个球一循环,
每个循环里有3个实心球,
因:2012÷10=201……2,
所以共有实心球3×201+1=604(个).
604
(2)按如图方式摆放餐桌和椅子,照这样的方式继续排列餐桌,
摆4张桌子可坐多少人
摆5张桌子呢
摆n张桌子呢
序号 1 2 3 4 5 … n
人数 6 10 14 18 22 …
4n+2
3.观察下列图形的排列规律(其中△是三角形,□是正方形,○是圆):
□○△□□○△□○△□□○△□○△□□○△□○△□□……
若第一个图形是正方形,则第2008个图形是 .(填图形名称)
解析:每7个图形一循环,因为2008÷7=286……6,
所以第2008个图形与第6个图形一样
圆
4.用黑白两种颜色的正六边形地砖按
如下所示的规律拼成若干个图案,第(4)
个图案中有黑色地砖4块,那么第(n)个
图案中有白色地砖 块.
……
(4n+2)
解:第1个图案有6块白色瓷砖,
第2个图案有10块白色瓷砖,
每多1块黑色瓷砖则多4块白色瓷砖,
根据此规律可知第n个图案中的白色瓷砖的块数为6+4(n-1),
即4n+2
探索规律的一般步骤
观察特例寻找数量关系
大胆猜想规律
用代数式表示规律
验证规律是否成立
得出结论
成立
不
成
立
课堂小结
数式变化中的规律
图形拼接中的规律
探索与表达规律
探索 猜想 验证
特殊 一般
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
