4.4 平行线的判定 (2)课件 (共16张PPT)湘教版七年级数学下册
文档属性
| 名称 | 4.4 平行线的判定 (2)课件 (共16张PPT)湘教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 12:38:46 | ||
图片预览






文档简介
(共16张PPT)
第4章 相交线与平行线
4.4 平行线的判定
第2课时
1.掌握平行线的判定方法②、③;
2.能用平行线的判定方法进行简单的推导和平行线的判定.
∵∠1=_____;
∴a//b( ).
3
a
b
c
1
2
4
∠2
同位角相等,两直线平行
根据平行线的判定填空.
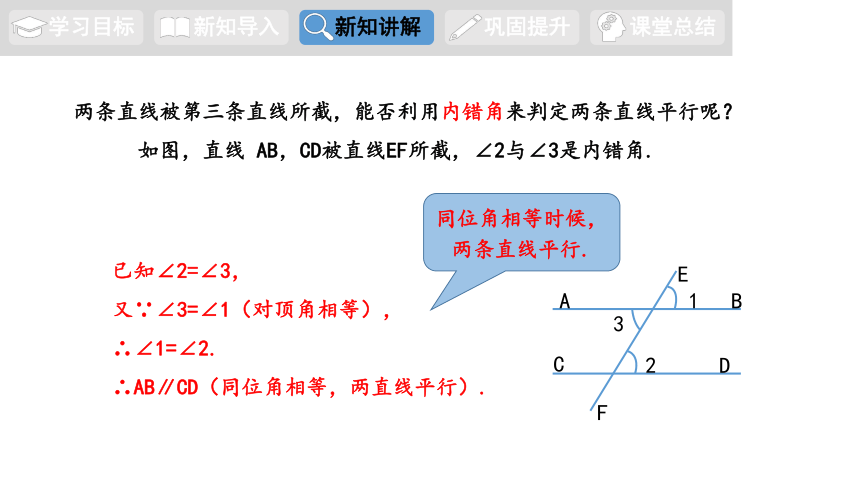
两条直线被第三条直线所截,能否利用内错角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠2与∠3是内错角.
1
3
2
A
B
C
D
E
F
已知∠2=∠3,
又∵∠3=∠1(对顶角相等),
∴∠1=∠2.
∴AB∥CD(同位角相等,两直线平行).
同位角相等时候,两条直线平行.
平行线的判定2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. (内错角相等,两直线平行)
∵∠3=∠2 (已知)
∴a∥b(内错角相等,两直线平行)
书写格式:
b
1
2
a
c
3
例1 如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解:∵AB∥DC,
∴∠1=∠2(两直线平行内错角相等).
又∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2.
即∠3=∠4.
∴ AD∥BC(内错角相等,两直线平行).
两条直线被第三条直线所截,能否利用同旁内角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠1与∠2是同旁内角.
∵∠1+∠2= 180o(已知),
且∠2+∠3= 180o,
∴∠3=∠1.
∴AB∥CD(同位角相等,两直线平行).
1
3
2
A
B
C
D
E
F
同位内角互补时,两条直线平行.
平行线的判定3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.(同旁内角互补,两直线平行)
∵∠4+∠2=180° (已知)
∴a∥b(同旁内角互补,两直线平行)
书写格式:
b
1
2
a
c
4
解:∵AD∥BC,
∴∠1+∠3=180°(两直线平行,同旁内角互补)
∴ AB∥DC(同旁内角互补,两直线平行).
例2 如图,∠1=∠2=50°,AD∥BC,那么 AB∥DC吗?
则∠3=180°-∠1=180°-50°=130°
∴∠2+∠3=50°+130°=180°
平行线的三个判定方法:
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定关系:
小结
1.判断:(打“√”或“×”)
(1)内错角互补,两直线平行.( )
(2)垂直于同一条直线的两条直线互相平行.( )
(3)同旁内角相等,两直线平行.( )
(4)利用直尺和三角板画已知直线的平行线的依据是“同位角相等,两直线平行”.( )
×
×
×
√
2.如图,点A在直线l上,如果∠B= 75°,∠C= 43° ,则
(1)当 ∠1= 时,直线l ∥BC;
(2)当 ∠2= 时,直线l ∥BC.
75°
43°
1
2
l
A
B
C
75°
43°
内错角相等,两条直线平行.
3.如图,∠ADE=∠DEF, ∠EFC+∠C=180°, 试问AD与 BC平行吗?为什么?
A
B
C
D
E
F
解:∵∠ADE=∠DEF,
∴AD∥EF (内错角相等,两直线平行).
∵∠EFC+∠C = 180°,
∴BC∥EF (同旁内角互补,两直线平行).
∴AD∥BC
4.如图,已知∠1=∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
相等 两直线平行 ∵ (已知) ∴a∥b 互补 两直线平行 ∵ (已知) ∴a∥b 平行线的判定方法:
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
第4章 相交线与平行线
4.4 平行线的判定
第2课时
1.掌握平行线的判定方法②、③;
2.能用平行线的判定方法进行简单的推导和平行线的判定.
∵∠1=_____;
∴a//b( ).
3
a
b
c
1
2
4
∠2
同位角相等,两直线平行
根据平行线的判定填空.
两条直线被第三条直线所截,能否利用内错角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠2与∠3是内错角.
1
3
2
A
B
C
D
E
F
已知∠2=∠3,
又∵∠3=∠1(对顶角相等),
∴∠1=∠2.
∴AB∥CD(同位角相等,两直线平行).
同位角相等时候,两条直线平行.
平行线的判定2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. (内错角相等,两直线平行)
∵∠3=∠2 (已知)
∴a∥b(内错角相等,两直线平行)
书写格式:
b
1
2
a
c
3
例1 如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解:∵AB∥DC,
∴∠1=∠2(两直线平行内错角相等).
又∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2.
即∠3=∠4.
∴ AD∥BC(内错角相等,两直线平行).
两条直线被第三条直线所截,能否利用同旁内角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠1与∠2是同旁内角.
∵∠1+∠2= 180o(已知),
且∠2+∠3= 180o,
∴∠3=∠1.
∴AB∥CD(同位角相等,两直线平行).
1
3
2
A
B
C
D
E
F
同位内角互补时,两条直线平行.
平行线的判定3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.(同旁内角互补,两直线平行)
∵∠4+∠2=180° (已知)
∴a∥b(同旁内角互补,两直线平行)
书写格式:
b
1
2
a
c
4
解:∵AD∥BC,
∴∠1+∠3=180°(两直线平行,同旁内角互补)
∴ AB∥DC(同旁内角互补,两直线平行).
例2 如图,∠1=∠2=50°,AD∥BC,那么 AB∥DC吗?
则∠3=180°-∠1=180°-50°=130°
∴∠2+∠3=50°+130°=180°
平行线的三个判定方法:
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定关系:
小结
1.判断:(打“√”或“×”)
(1)内错角互补,两直线平行.( )
(2)垂直于同一条直线的两条直线互相平行.( )
(3)同旁内角相等,两直线平行.( )
(4)利用直尺和三角板画已知直线的平行线的依据是“同位角相等,两直线平行”.( )
×
×
×
√
2.如图,点A在直线l上,如果∠B= 75°,∠C= 43° ,则
(1)当 ∠1= 时,直线l ∥BC;
(2)当 ∠2= 时,直线l ∥BC.
75°
43°
1
2
l
A
B
C
75°
43°
内错角相等,两条直线平行.
3.如图,∠ADE=∠DEF, ∠EFC+∠C=180°, 试问AD与 BC平行吗?为什么?
A
B
C
D
E
F
解:∵∠ADE=∠DEF,
∴AD∥EF (内错角相等,两直线平行).
∵∠EFC+∠C = 180°,
∴BC∥EF (同旁内角互补,两直线平行).
∴AD∥BC
4.如图,已知∠1=∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
相等 两直线平行 ∵ (已知) ∴a∥b 互补 两直线平行 ∵ (已知) ∴a∥b 平行线的判定方法:
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
