5.2 旋转 课件 (共19张PPT)湘教版七年级数学下册
文档属性
| 名称 | 5.2 旋转 课件 (共19张PPT)湘教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 718.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 12:39:50 | ||
图片预览




文档简介
(共19张PPT)
第5章 轴对称与旋转
5.2 旋转
1.理解旋转及相关概念,掌握旋转的性质;
2.能运用旋转的性质解决相关问题,并能画旋转图形.
1.平移:把图形上所有的点都按 移动相同的 ,图形的这种变换叫做平移.
2.性质:
(1)平移前后的两个图形的 和 完全相同,改变的只是图形的 .
(2)平移不改变直线的 .
(3)一个图形和它经过平移所得的图形中,两组对应点的连线 (或在同一条直线上)且 .
同一方向
距离
形状
大小
位置
方向
平行
相等
汽车的雨刮器绕支点旋转
如图 ,观察钟表的指针,电风扇的叶片,汽车的雨刮器在转动的过程中有什么共同的特征呢?
钟表的指针绕中间的固定点旋转
电风扇的叶片绕电机的轴旋转
都会绕一个定点旋转一定的角度.
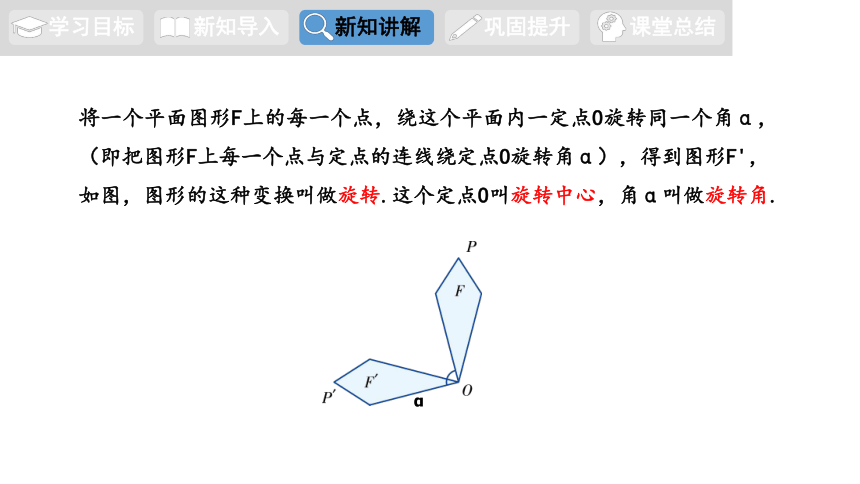
将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',
如图,图形的这种变换叫做旋转.这个定点O叫旋转中心,角α叫做旋转角.
α
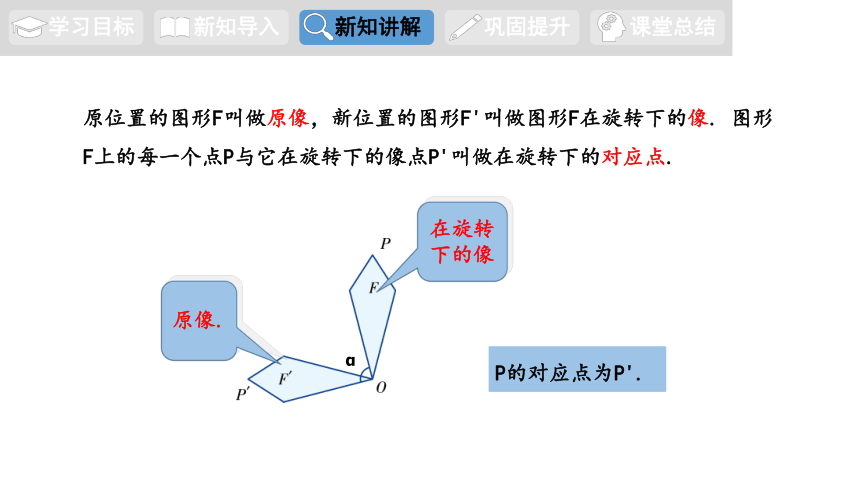
原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像. 图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
原像.
在旋转下的像
P的对应点为P'.
α
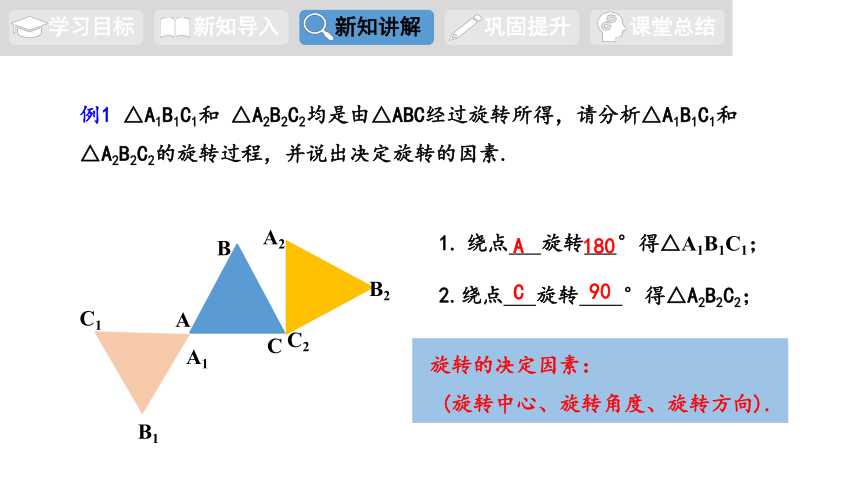
例1 △A1B1C1和 △A2B2C2均是由△ABC经过旋转所得,请分析△A1B1C1和△A2B2C2的旋转过程,并说出决定旋转的因素.
1. 绕点 旋转 °得△A1B1C1;
2.绕点 旋转 °得△A2B2C2;
C
C2
B2
A2
B
A
A1
C1
B1
A
180
C
90
旋转的决定因素:
(旋转中心、旋转角度、旋转方向).
1.如图 ,将三角形ABC按逆时针方向绕点O旋转60 得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?
A'
B'
C'
A
B
C
O
.
.
P '
P
60
由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60 =∠AOA'.
2.当三角形ABC旋转到新的位置,得到三角形A'B'C',它的形状和大小发生变化了吗?
A'
B'
C'
A
B
C
O
.
.
P '
P
60
旋转前后,形状、大小都没有发生变化.
知识探究
1.一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.
旋转的性质:
2.旋转不改变图形的形状和大小. .
B
A
C
O
平移 旋转
相同 1.都是一种运动; 2.运动前后不改变图形的形状和大小. 不同 运动方向 直线 顺时针或逆时针
运动量衡量 移动一定距离 转动一定的角度
平移
旋转
知识总结
例2 如图,将三角形ABC按逆时针方向旋转45 ,得到三角形AB'C'.
(1)图中哪一点是旋转中心?
(2)∠B'CB和∠C'AC有何关系?它们的度数是多少?
(3)AB与AB',AC与AC'有何关系?
解:(1)点A是旋转中心.
∴∠B'AB=∠C'AC=45 .
(两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角 )
(3)∵对应点到旋转中心的距离相等,
(2)∵B与B',C与C'是对应点.
∴AB=AB',AC=AC'.
例3 已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形.
B
A
O
A'
B'
⑴.连接OA
⑵.作∠AOC=100°,
(5).作∠BOD=100°,
(7).连接A'B'线段A'B'就是线段AB绕点O按逆时针方向旋转100°后的对应线段.
C
D
(4).连接OB
(3).在OC上截取OA'=OA
(6).在OD上截取OB'=OB
注:作旋转后的图形可以转化为作旋转后的对应点
1.判断题:对的打“√”,错的打“×”)
(1)图形的旋转是由旋转中心决定的.( )
(2)图形的旋转过程中,旋转中心是保持不动的.( )
(3)旋转中心不同,旋转后图形的形状就不同.( )
(4)正方形旋转90°后能与原来的正方形重合.( )
(5)旋转的原象与象的对应点到旋转中心的距离相等.( )
×
√
×
×
√
2.下列运动属于旋转的是( )
A.滚动过程中的篮球 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折的过程
解析:A选项滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B选项钟表的钟摆的摆动,符合旋转的定义,属于旋转;C选项气球升空的运动不属于旋转;D选项一个图形沿某直线对折的过程是轴对称,不属于旋转.
B
3.如图所示,在正方形网格中,图①经过 变换可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”).
解析:观察可得:图①与图②对应点位置不变,通过平移可以得到;根据旋转中心的确定方法,两组对应点连线的垂直平分线的交点,可确定图②经过旋转变换得到图③的旋转中心是A.
平移
A
4.如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到△AB‘C’,则∠BAC'等于( )
A.60° B.105° C.120° D.135°
解析:因为在等腰直角三角形ABC中,∠B=90°,
将△ABC绕点A逆时针旋转60°后得到△AB'C',
所以∠CAC'=60°,所以∠BAC'=45°+60°=105°.
B
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD、∠BOE
B
A
C
O
D
E
F
5.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
将一个平面图形F上的每一个点,绕这个平面内一定点旋转同一个角,得到图形F',图形的这种变换叫做旋转.这个定点叫旋转中心,角叫做旋转角.
2.旋转的性质:
①一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.
②旋转不改变图形的形状和大小.
1.旋转:
第5章 轴对称与旋转
5.2 旋转
1.理解旋转及相关概念,掌握旋转的性质;
2.能运用旋转的性质解决相关问题,并能画旋转图形.
1.平移:把图形上所有的点都按 移动相同的 ,图形的这种变换叫做平移.
2.性质:
(1)平移前后的两个图形的 和 完全相同,改变的只是图形的 .
(2)平移不改变直线的 .
(3)一个图形和它经过平移所得的图形中,两组对应点的连线 (或在同一条直线上)且 .
同一方向
距离
形状
大小
位置
方向
平行
相等
汽车的雨刮器绕支点旋转
如图 ,观察钟表的指针,电风扇的叶片,汽车的雨刮器在转动的过程中有什么共同的特征呢?
钟表的指针绕中间的固定点旋转
电风扇的叶片绕电机的轴旋转
都会绕一个定点旋转一定的角度.
将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',
如图,图形的这种变换叫做旋转.这个定点O叫旋转中心,角α叫做旋转角.
α
原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像. 图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
原像.
在旋转下的像
P的对应点为P'.
α
例1 △A1B1C1和 △A2B2C2均是由△ABC经过旋转所得,请分析△A1B1C1和△A2B2C2的旋转过程,并说出决定旋转的因素.
1. 绕点 旋转 °得△A1B1C1;
2.绕点 旋转 °得△A2B2C2;
C
C2
B2
A2
B
A
A1
C1
B1
A
180
C
90
旋转的决定因素:
(旋转中心、旋转角度、旋转方向).
1.如图 ,将三角形ABC按逆时针方向绕点O旋转60 得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?
A'
B'
C'
A
B
C
O
.
.
P '
P
60
由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60 =∠AOA'.
2.当三角形ABC旋转到新的位置,得到三角形A'B'C',它的形状和大小发生变化了吗?
A'
B'
C'
A
B
C
O
.
.
P '
P
60
旋转前后,形状、大小都没有发生变化.
知识探究
1.一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.
旋转的性质:
2.旋转不改变图形的形状和大小. .
B
A
C
O
平移 旋转
相同 1.都是一种运动; 2.运动前后不改变图形的形状和大小. 不同 运动方向 直线 顺时针或逆时针
运动量衡量 移动一定距离 转动一定的角度
平移
旋转
知识总结
例2 如图,将三角形ABC按逆时针方向旋转45 ,得到三角形AB'C'.
(1)图中哪一点是旋转中心?
(2)∠B'CB和∠C'AC有何关系?它们的度数是多少?
(3)AB与AB',AC与AC'有何关系?
解:(1)点A是旋转中心.
∴∠B'AB=∠C'AC=45 .
(两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角 )
(3)∵对应点到旋转中心的距离相等,
(2)∵B与B',C与C'是对应点.
∴AB=AB',AC=AC'.
例3 已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形.
B
A
O
A'
B'
⑴.连接OA
⑵.作∠AOC=100°,
(5).作∠BOD=100°,
(7).连接A'B'线段A'B'就是线段AB绕点O按逆时针方向旋转100°后的对应线段.
C
D
(4).连接OB
(3).在OC上截取OA'=OA
(6).在OD上截取OB'=OB
注:作旋转后的图形可以转化为作旋转后的对应点
1.判断题:对的打“√”,错的打“×”)
(1)图形的旋转是由旋转中心决定的.( )
(2)图形的旋转过程中,旋转中心是保持不动的.( )
(3)旋转中心不同,旋转后图形的形状就不同.( )
(4)正方形旋转90°后能与原来的正方形重合.( )
(5)旋转的原象与象的对应点到旋转中心的距离相等.( )
×
√
×
×
√
2.下列运动属于旋转的是( )
A.滚动过程中的篮球 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折的过程
解析:A选项滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B选项钟表的钟摆的摆动,符合旋转的定义,属于旋转;C选项气球升空的运动不属于旋转;D选项一个图形沿某直线对折的过程是轴对称,不属于旋转.
B
3.如图所示,在正方形网格中,图①经过 变换可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”).
解析:观察可得:图①与图②对应点位置不变,通过平移可以得到;根据旋转中心的确定方法,两组对应点连线的垂直平分线的交点,可确定图②经过旋转变换得到图③的旋转中心是A.
平移
A
4.如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到△AB‘C’,则∠BAC'等于( )
A.60° B.105° C.120° D.135°
解析:因为在等腰直角三角形ABC中,∠B=90°,
将△ABC绕点A逆时针旋转60°后得到△AB'C',
所以∠CAC'=60°,所以∠BAC'=45°+60°=105°.
B
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD、∠BOE
B
A
C
O
D
E
F
5.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
将一个平面图形F上的每一个点,绕这个平面内一定点旋转同一个角,得到图形F',图形的这种变换叫做旋转.这个定点叫旋转中心,角叫做旋转角.
2.旋转的性质:
①一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.
②旋转不改变图形的形状和大小.
1.旋转:
