4.4 平行线的判定 (1)课件(共17张PPT) 湘教版七年级数学下册
文档属性
| 名称 | 4.4 平行线的判定 (1)课件(共17张PPT) 湘教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 12:40:19 | ||
图片预览




文档简介
(共17张PPT)
第4章 相交线与平行线
4.4 平行线的判定
第1课时
1.掌握直线平行的基本事实;
2.能利用平行线的判定方法①进行简单的推导和平行线判定.
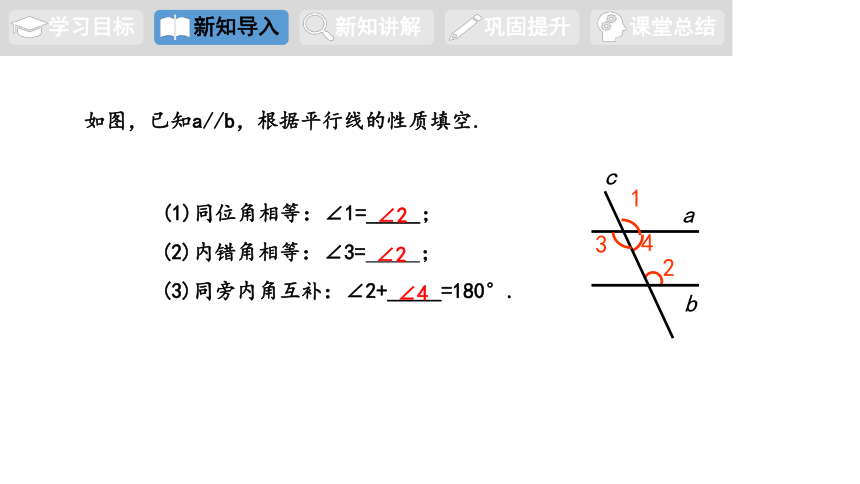
(1)同位角相等:∠1=_____;
(2)内错角相等:∠3= ;
(3)同旁内角互补:∠2+_____=180°.
3
a
b
c
1
2
4
∠2
∠2
∠4
如图,已知a//b,根据平行线的性质填空.
b
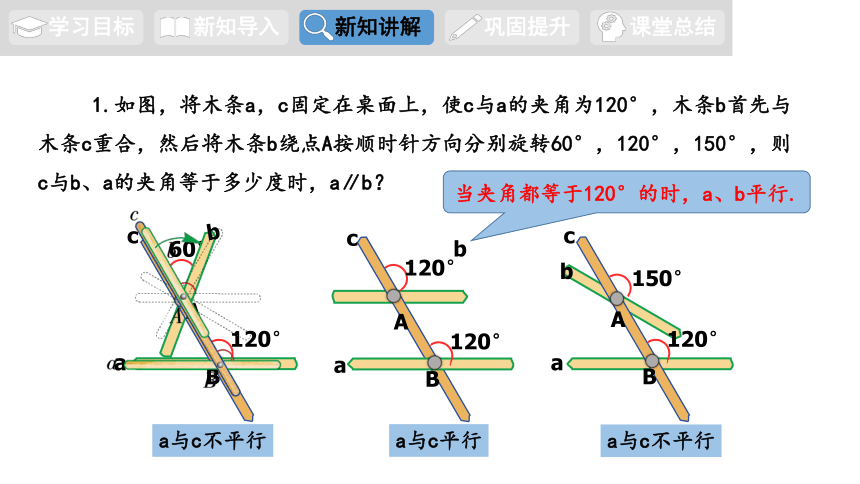
1.如图,将木条a,c固定在桌面上,使c与a的夹角为120°,木条b首先与木条c重合,然后将木条b绕点A按顺时针方向分别旋转60°,120°,150°,则c与b、a的夹角等于多少度时,a∥b?
60°
120°
b
120°
c
a
A
B
120°
c
a
A
B
b
120°
c
a
A
B
150°
a与c不平行
a与c平行
a与c不平行
当夹角都等于120°的时,a、b平行.
2.如图,将木条c与b、a的夹角属于什么角?当其等于多少度时,a∥b?
b
120°
120°
c
a
A
B
c与b、a所成的夹角是同位角,当同位角相等,都等于120°时,a//b.
根据这些操作,你能猜想出什么结论?
我们猜想:如果两条直线被第三条直线所截,若同位角相等,则这两条直 线平行.
这个猜想对吗?
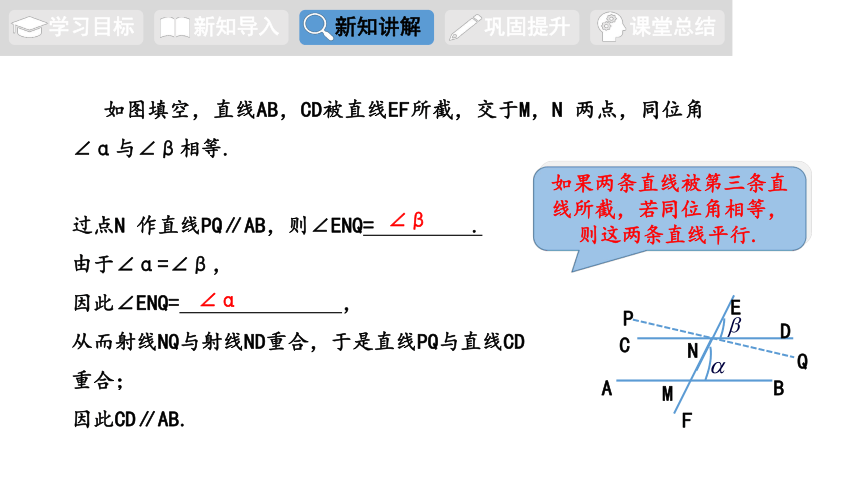
过点N 作直线PQ∥AB,则∠ENQ= .
由于∠α=∠β,
因此∠ENQ= ,
从而射线NQ与射线ND重合,于是直线PQ与直线CD重合;
因此CD∥AB.
如图填空,直线AB,CD被直线EF所截,交于M,N 两点,同位角∠α与∠β相等.
∠β
∠α
A
B
C
D
E
F
M
N
P
Q
如果两条直线被第三条直线所截,若同位角相等,则这两条直线平行.
平行线的判定:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.(同位角相等,两直线平行)
b
1
2
a
c
∵∠1=∠2 (已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
例1 如图,直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗? 为什么?
解:∵∠1+∠2 =180°,
且∠1+∠3=180°
∴∠2=∠3
∴AB∥CD (同位角相等,两直线平行)
我们学习了一种画平行线的方法(如图),你能说明这种画法的理由吗?
C
B
C’
B’
同位角相等,两直线平行
例2 如图,直线a,b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
解:∵∠1=∠2(已知),
∴∠1=∠3(等量代换)
∴a∥b(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等).
且∠2=∠3 (对顶角相等)
1. 如图,木工用角尺的一边紧靠木料边缘,另一边画两条直线a,b.这两条直线平行吗?为什么?
解:a∥b.
因为有一对同位角都是直角.
2. 根据下图,填空:从∠5=∠ ,可以推出AB∥CD,
理由是 .
A
B
C
D
1
2
3
4
5
ABC
同位角相等,两直线平行
3.如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解:∵∠EGB=90° ,∠E=30°,(已知)
∴∠EKG=180°-90°-∠E
=60°(三角形内角和为180°)
∴∠AKF=∠EKG=60°(对顶角相等)
∴∠AKF=∠CHF=60°
∴AB∥CD(同位角相等,两直线平行)
4.如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解:AD∥BC.理由如下:
∵AB∥DC(已知),
∴∠A+∠D=180°(两直线平行,同旁内角互补).
∵∠D=125°(已知),
∴∠A=180°-∠D=180°-125°=55°.
∵∠CBE=55°(已知),
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行).
B
A
D
C
E
5.如图,在△ABC中,D,E分别在AC,BC上,∠C=20°,∠CDE=120°, ∠B=40°,请问DE与AB是否平行?并说明理由.
解:DE∥AB.理由如下:
在△CDE中,∠CDE=120°,∠C=20°,
∵∠CDE+∠C+∠DEC=180°,
∴∠DEC=180°-∠CDE-∠C=180°-120°-20°=40°,
又∵∠B=40°,∴∠DEC=∠B=40°,
∴DE∥AB(同位角相等,两直线平行).
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.(同位角相等,两直线平行)
平行线的判定:
第4章 相交线与平行线
4.4 平行线的判定
第1课时
1.掌握直线平行的基本事实;
2.能利用平行线的判定方法①进行简单的推导和平行线判定.
(1)同位角相等:∠1=_____;
(2)内错角相等:∠3= ;
(3)同旁内角互补:∠2+_____=180°.
3
a
b
c
1
2
4
∠2
∠2
∠4
如图,已知a//b,根据平行线的性质填空.
b
1.如图,将木条a,c固定在桌面上,使c与a的夹角为120°,木条b首先与木条c重合,然后将木条b绕点A按顺时针方向分别旋转60°,120°,150°,则c与b、a的夹角等于多少度时,a∥b?
60°
120°
b
120°
c
a
A
B
120°
c
a
A
B
b
120°
c
a
A
B
150°
a与c不平行
a与c平行
a与c不平行
当夹角都等于120°的时,a、b平行.
2.如图,将木条c与b、a的夹角属于什么角?当其等于多少度时,a∥b?
b
120°
120°
c
a
A
B
c与b、a所成的夹角是同位角,当同位角相等,都等于120°时,a//b.
根据这些操作,你能猜想出什么结论?
我们猜想:如果两条直线被第三条直线所截,若同位角相等,则这两条直 线平行.
这个猜想对吗?
过点N 作直线PQ∥AB,则∠ENQ= .
由于∠α=∠β,
因此∠ENQ= ,
从而射线NQ与射线ND重合,于是直线PQ与直线CD重合;
因此CD∥AB.
如图填空,直线AB,CD被直线EF所截,交于M,N 两点,同位角∠α与∠β相等.
∠β
∠α
A
B
C
D
E
F
M
N
P
Q
如果两条直线被第三条直线所截,若同位角相等,则这两条直线平行.
平行线的判定:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.(同位角相等,两直线平行)
b
1
2
a
c
∵∠1=∠2 (已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
例1 如图,直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗? 为什么?
解:∵∠1+∠2 =180°,
且∠1+∠3=180°
∴∠2=∠3
∴AB∥CD (同位角相等,两直线平行)
我们学习了一种画平行线的方法(如图),你能说明这种画法的理由吗?
C
B
C’
B’
同位角相等,两直线平行
例2 如图,直线a,b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
解:∵∠1=∠2(已知),
∴∠1=∠3(等量代换)
∴a∥b(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等).
且∠2=∠3 (对顶角相等)
1. 如图,木工用角尺的一边紧靠木料边缘,另一边画两条直线a,b.这两条直线平行吗?为什么?
解:a∥b.
因为有一对同位角都是直角.
2. 根据下图,填空:从∠5=∠ ,可以推出AB∥CD,
理由是 .
A
B
C
D
1
2
3
4
5
ABC
同位角相等,两直线平行
3.如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解:∵∠EGB=90° ,∠E=30°,(已知)
∴∠EKG=180°-90°-∠E
=60°(三角形内角和为180°)
∴∠AKF=∠EKG=60°(对顶角相等)
∴∠AKF=∠CHF=60°
∴AB∥CD(同位角相等,两直线平行)
4.如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解:AD∥BC.理由如下:
∵AB∥DC(已知),
∴∠A+∠D=180°(两直线平行,同旁内角互补).
∵∠D=125°(已知),
∴∠A=180°-∠D=180°-125°=55°.
∵∠CBE=55°(已知),
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行).
B
A
D
C
E
5.如图,在△ABC中,D,E分别在AC,BC上,∠C=20°,∠CDE=120°, ∠B=40°,请问DE与AB是否平行?并说明理由.
解:DE∥AB.理由如下:
在△CDE中,∠CDE=120°,∠C=20°,
∵∠CDE+∠C+∠DEC=180°,
∴∠DEC=180°-∠CDE-∠C=180°-120°-20°=40°,
又∵∠B=40°,∴∠DEC=∠B=40°,
∴DE∥AB(同位角相等,两直线平行).
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.(同位角相等,两直线平行)
平行线的判定:
