2015年中考数学易错题赏析:(十)填空题之压轴题
文档属性
| 名称 | 2015年中考数学易错题赏析:(十)填空题之压轴题 |

|
|
| 格式 | zip | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-19 07:33:57 | ||
图片预览




文档简介
(十)填空题之压轴题
题型特点
填空题与选择题相比,没有选项,因此没有错误选项的干扰,但也就缺少了有关信息提示,给解题增加了一定难度,要求学生要有扎实、熟练的基础知识和基本技能.还要灵活运用多种不同的解题方法.21世纪教育网版权所有
解题方法
解答填空题常用的方法有直接求解法、数形结合法、构造法、分类讨论法与转化法等.直接求解法就是从已知出发,逐步计算推出未知的方法,或者说由“因”索“果”的方法.很多题目都需要将题目中的条件与相关图形或图象结合起来考察,这就是数形结合法.有时在分析解题过程中所需要或所缺少的有关条件可通过作辅助线或建立模型等方法来解决问题的方法就是构造法.在题目的相关条件或信息不够明确具体时,则应分情况求解,也就是分类讨论法.把不易解决的问题或难点,通过第三个等价的量,转化为已知的或易于解决的问题来解题的方法就是转化法.2·1·c·n·j·y
易错题赏析
易错题1:在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,…. 21*cnjy*com
(1)若点A1的坐标为(3,1),则点A3的坐标为__________,点A2014的坐标为__________;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴下方,则a,b应满足的条件为___________________________________.【来源:21·世纪·教育·网】
答案:(1)(﹣3,1),(0,4);
(2)﹣1<a<1且0<b<2.
解答:∵点A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),A6(0,4),A7(﹣3,1),A8(0,﹣2),…,
依此类推,每4个点为一个循环组,依次循环.
∵2014÷4=503余2,
∴点A2014的坐标与点A2的坐标相同,为(0,4).
∵点A1的坐标为(a,b),
∴A2(﹣b+1,a+1),A3(﹣a,﹣b+2),A4(b-1,﹣a+1),A5(a,b),A6(﹣b+1,a+1),A7(﹣a,﹣b+2),A8(b-1,﹣a+1),…,
依此类推,每4个点为一个循环组,依次循环.
∵对于任意的正整数n,点An均在x轴上方,
而位于x轴上方的点纵坐标大于0,
∴可得且,
解得﹣1<a<1且0<b<2.
赏析:本题主要采用定义法、列举法、归纳法与模型法.首先根据伴随点的定义依次列举各点(一部分点如8个点即可),再观察归纳得出规律“每4个点为一个循环组依次循环”,并由此规律用2014除以4,根据商和余数可求点A2014的坐标;根据定义列举点A1(a,b)(一部分),再由题目条件建立不等式组模型求解.解题关键是理解伴随点的定义得出规律并建立不等式组模型.【出处:21教育名师】
易错题2:如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则的值为__________________.www.21-cn-jy.com
答案:
解答:已知AD为△ABC的角平分线,则点D到AB、AC的距离相等,设为h.
∵,∴BD=CD.
如下图,延长AC,在AC的延长线时截取AM=AB,则有AC=AM,CM=AC,连接DM,在△ABD和△AMD中,∵,∴△ABD≌△AMD(SAS),∴MD=BD=CD ,过点M作MN∥AD,交EG于点N,交DE于点K.∵MN∥AD,∴,∴CK=CD,∴KD=CD,∴MD=KD,△DMK为等腰三角形,∴∠DMK=∠DKM,由题意得△EDG为等腰三角形,∠1=∠2,∵MN∥AD,∴∠3=∠4=∠1=∠2,又∵∠DKM=∠DMK=∠3,∴∠DMK=∠4,∴DM∥GN,∴四边形DMNG为平行四边形,∴MN=DG=2FD,∵点H为AC的中点,AC=AM,CM=AC,∴,∵MN∥AD,∴,即,∴.
赏析:本题主要采用构造法,构造全等三角形,平行四边形与等腰三角形;还用到了面积法,如用面积法得到BD=CD;还有转化法,将有关线段、比例线段多次转化,最终求得结果.本题是三角形的综合题,每一种方法都是解题关键,特别是有关线段、比例线段的多次转化,极易出错,解题一定要仔细.
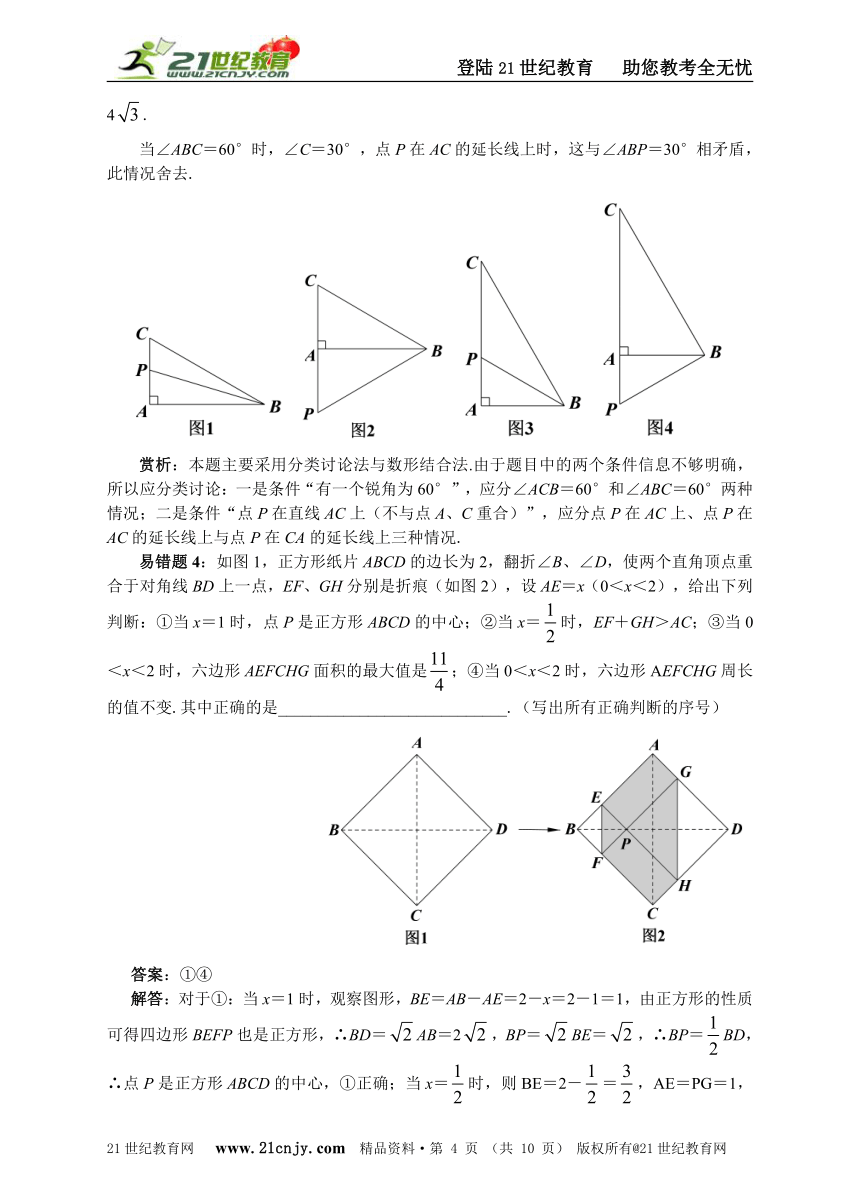
易错题3:在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A、C重合),且∠ABP=30°,则CP的长为____________________.
答案:6或2或4
解答:如图1,当∠C=60°时,∠ABC=30°,点P在AC上或AC的延长线上时,这与∠ABP=30°相矛盾,此情况舍去;
如图2,当∠C=60°时,∠ABC=30°,点P在CA的延长线上时,∵∠ABP=30°,∴△ABC≌△ABP(ASA),∴∠CBP=∠ABC+∠ABP=30°+30°=60°,BC=BP,∴△PBC为等边三角形,∴CP=BC=6;21*cnjy*com
如图3,当∠ABC=60°时,∠C=30°,点P在AC上时,∵∠ABP=30°,∴∠PBC=∠ABC-∠ABP=60°-30°=30°,∴∠PBC=∠C,∴PC=PB,∵BC=6,∴AB=BC=3,∴PC=PB====2;
如图4,当∠ABC=60°时,∠C=30°,点P在CA的延长线上时,∵∠ABP=30°,∴∠PBC=∠ABC+∠ABP=60°+30°=90°,∴在Rt△PBC中,PC===4. 【来源:21cnj*y.co*m】
当∠ABC=60°时,∠C=30°,点P在AC的延长线上时,这与∠ABP=30°相矛盾,此情况舍去.【版权所有:21教育】
赏析:本题主要采用分类讨论法与数形结合法.由于题目中的两个条件信息不够明确,所以应分类讨论:一是条件“有一个锐角为60°”,应分∠ACB=60°和∠ABC=60°两种情况;二是条件“点P在直线AC上(不与点A、C重合)”,应分点P在AC上、点P在AC的延长线上与点P在CA的延长线上三种情况.
易错题4:如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角顶点重合于对角线BD上一点,EF、GH分别是折痕(如图2),设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的是____________________________.(写出所有正确判断的序号)
答案:①④
解答:对于①:当x=1时,观察图形,BE=AB-AE=2-x=2-1=1,由正方形的性质可得四边形BEFP也是正方形,∴BD=AB=2,BP=BE=,∴BP=BD,∴点P是正方形ABCD的中心,①正确;当x=时,则BE=2-=,AE=PG=1,又观察图形得四边形PHDG也是正方形,∴EF=BE=,GH=PG=,∴EF+GH=+=2,又∵AC=AB=2,∴EF+GH=AC,②错误; 对于③:当0<x<2时,设六边形AEFCHG面积为S,∵AB=2,AE=x,∴BE=BF=2-x,DG=DH=x,∴S=S正方形ABCD-S△BEF-S△GDH=2×2―(2-x)2―x2=﹣(x-1)2+3,当x=1时,S最大值=3,∴当x=1时,六边形AEFCHG面积的最大值是3,③错误;④当0<x<2时,设六边形AEFCHG周长为m,观察图形得m=AE+EF+FC+CH+HG+GA=AE+BP+FC+BF+PD+BE=AB+BC+BD=4+2,∴当0<x<2时,六边形AEFCHG周长的值不变,④正确.21教育网
赏析:本题主要采用了函数模型法和数形结合法.对于③④,分别建立二次函数与常数函数模型来求解,而每一结论都要通过观察图形,特别是图形中的正方形,矩形,等腰直角三角形,将一些相等的线段进行等量转换,使问题得以解决.
易错题5:如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在 BC上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是______________________.2-1-c-n-j-y
答案:①③⑤
解答:对于①:如图1,连接CD,∵点E与点D关于AC对称,∴CE=CD,∴∠E=∠CDE,∵DF⊥DE,∴∠EDF=90°,∴∠E+∠F=90°,∠CDE+∠CDF=90°,∴∠F=∠CDF,∴CE=CD=CF,∴①正确;21·世纪*教育网
对于②:如图2,当CD⊥AB时,∵AB是半圆的直径,∴∠ACB=90°,∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=4,∵CD⊥AB,∠CBA=30°,∴CD=BC=2,由“垂线段最短”得点D在AB上运动时,CD的最小值为2,∵CE=CD=CF,∴线段EF的最小值为4,∴②错误;
对于③:如图3,当AD=2时,连接OC,∵OA=OC,∠CAB=60°,∴△OAC是等边三角形,∴CA=CO,∠ACO=60°,∵AO=4,AD=2,∴DO=2,∴AD=DO,∴∠ACD=∠DCO=30°,∵点E与点D关于AC对称,∴∠ECA=∠DCA,∴∠ECA=30°,∴∠ECO=90°,∴OC⊥EF,∵EF经过半径OC外端,且OC⊥EF,∴EF与半圆相切,∴③正确;21cnjy.com
对于④:如图4,当点F恰好落在BC上时,连接FB、AF,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴,∵FC=EF,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∵BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=AB=4,∵DB=4,∴AD=AB-DB=4,∴④错误;
对于⑤:如图5,∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称,∴EF扫过的图形就是图5中的阴影部分,∴S阴影=2S△ABC=2××AC×BC=AC×BC=4×4=16,∴当点D从点A运动到点B时,线段EF扫过的面积是16,∴⑤正确.21教育名师原创作品
赏析:本题主要运用了直接求解法,构造法,运动轨迹法与面积法.这是一道圆的综合题,它综合了直角三角形,等边三角形,相似三角形,圆周角定理,圆的切线的判定,三角形面积的求法,轴对称等内容,轴对称性在本题中起着重要的作用,特别是⑤中轴对称性的运用是解决此问的关键.
易错练
1.如图,B为双曲线y=(x>0)上一点,直线AB∥y轴交直线y=x于点A,若OB2-AB2=12,则k=_______________.
2.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是______________________.
3.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=,DE交AC于点E,且cos=,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或;④0<CE≤6.4.其中正确的结论是___________________________.(填序号)
4.如图,在边长为6的正方形ABCD中,E是BC边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH,若BH=8,则FG=_____________.
5.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是__________________.
参考答案
易错练
1.6 赏析:如下图,延长AB交x轴于点C,设点C的横坐标为a,则点B的纵坐标为,点A的纵坐标为a,∴AB=a-.∵AB∥y轴,∴AC⊥OC.在Rt△BOC中,OB2=OC2+BC2=a2+()2,∵OB2-AB2=12,∴a2+()2-(a-)2=12,解得k=12.
2.﹣2<k< 赏析:由图可知,∠AOB=45°,∴直线OA的解析式为y=x.联立两个解析式得,消去y得x2-2x+2k=0,当△=b2-4ac=(﹣2)2-4×1×2k=0,即k=时,抛物线与OA有一个交点,此交点横坐标为1.∵点B的坐标为(2,0),∴OA=2,如下图,过点A作AC⊥OB于点C,则OC=CA=OAcos45°=2×=,∴点A的坐标为(,),交点在线段OA上;当抛物线经过点B(2,0)时,×22+k=0,解得k=﹣2.∴要使抛物线y=x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k<.21·cn·jy·com
3.①②③④ 赏析:对于①:∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B,∴∠ADE=∠C,∴△ADE∽△ACD,∴①正确;对于②:如下图,过点A作AF⊥BC于点F,∵AB=AC=
△DCE(ASA),∴②正确;对于③:当∠CED=90°时,则∠AED=90°,由①知,△ADE∽△ACD,∴∠ADC=∠AED,∵∠AED=90°,∴∠ADC=90°,即AD⊥BC,∵AB=AC,∴BD=CD,∴∠ADE=∠B=,cos=,AB=10,BD=8.当∠CDE=90°时,易证△CDE∽△BAD,∵∠CDE=90°,∴∠BAD=90°,∵∠B=,cos=,AB=10,∴cos∠B==,AB=10,∴BD=,∴③正确;对于④:易证△CDE∽△BAD,由①可知,BC=6,设BD=y,CE=x,∴,∴,∴y2-16y+64=64-10x,即(y-8)2=64-10x,∴64-10x≥0,解得x≤6.4,∴0<x≤6.4,∴④正确.
4.5 赏析:如图,连接CG,在△CGD与△CEB中,∵,∴△CGD≌△CEB(SAS),∴CG=CE,∠GCD=∠ECB,∴∠GCE=90°,即△GCE是等腰直角三角形.又∵CH⊥GE,∴CH=EH=GH.过点H作HM⊥AB于点M,HN⊥BC于点N,则∠MHN=90°,∴∠1=∠2,∴∠HEM=∠HCN.在△HEM与△HCN中,∵,∴△HEM≌△HCN(ASA),∴HM=HN,∴四边形MBNH是正方形.∵AH=8,∴BN=HN=4,∴CN=BC-BN=6-4=2.在Rt△HCN中,由勾股定理得CH=2,∴GH=CH=2,∵HM∥AG,∴∠1=∠3,∴∠2=∠3,又∵∠HNC=∠GHF=90°,∴Rt△HCN∽Rt△GFH,∴,∴,∴FG=5.www-2-1-cnjy-com
5.2≤AD<3 赏析:以D为圆心,AD长为半径画圆.①如图1,当圆与BC相切时,DE⊥BC.∵∠ABC=30°,∴DE=BD,∵AB=6,AD=DE,∴AD=2;②如图2,当圆与BC相交时,若交点为B或C时,都有AD=AB=3.∴AD的取值范围是2≤AD<3.
题型特点
填空题与选择题相比,没有选项,因此没有错误选项的干扰,但也就缺少了有关信息提示,给解题增加了一定难度,要求学生要有扎实、熟练的基础知识和基本技能.还要灵活运用多种不同的解题方法.21世纪教育网版权所有
解题方法
解答填空题常用的方法有直接求解法、数形结合法、构造法、分类讨论法与转化法等.直接求解法就是从已知出发,逐步计算推出未知的方法,或者说由“因”索“果”的方法.很多题目都需要将题目中的条件与相关图形或图象结合起来考察,这就是数形结合法.有时在分析解题过程中所需要或所缺少的有关条件可通过作辅助线或建立模型等方法来解决问题的方法就是构造法.在题目的相关条件或信息不够明确具体时,则应分情况求解,也就是分类讨论法.把不易解决的问题或难点,通过第三个等价的量,转化为已知的或易于解决的问题来解题的方法就是转化法.2·1·c·n·j·y
易错题赏析
易错题1:在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,…. 21*cnjy*com
(1)若点A1的坐标为(3,1),则点A3的坐标为__________,点A2014的坐标为__________;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴下方,则a,b应满足的条件为___________________________________.【来源:21·世纪·教育·网】
答案:(1)(﹣3,1),(0,4);
(2)﹣1<a<1且0<b<2.
解答:∵点A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),A6(0,4),A7(﹣3,1),A8(0,﹣2),…,
依此类推,每4个点为一个循环组,依次循环.
∵2014÷4=503余2,
∴点A2014的坐标与点A2的坐标相同,为(0,4).
∵点A1的坐标为(a,b),
∴A2(﹣b+1,a+1),A3(﹣a,﹣b+2),A4(b-1,﹣a+1),A5(a,b),A6(﹣b+1,a+1),A7(﹣a,﹣b+2),A8(b-1,﹣a+1),…,
依此类推,每4个点为一个循环组,依次循环.
∵对于任意的正整数n,点An均在x轴上方,
而位于x轴上方的点纵坐标大于0,
∴可得且,
解得﹣1<a<1且0<b<2.
赏析:本题主要采用定义法、列举法、归纳法与模型法.首先根据伴随点的定义依次列举各点(一部分点如8个点即可),再观察归纳得出规律“每4个点为一个循环组依次循环”,并由此规律用2014除以4,根据商和余数可求点A2014的坐标;根据定义列举点A1(a,b)(一部分),再由题目条件建立不等式组模型求解.解题关键是理解伴随点的定义得出规律并建立不等式组模型.【出处:21教育名师】
易错题2:如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则的值为__________________.www.21-cn-jy.com
答案:
解答:已知AD为△ABC的角平分线,则点D到AB、AC的距离相等,设为h.
∵,∴BD=CD.
如下图,延长AC,在AC的延长线时截取AM=AB,则有AC=AM,CM=AC,连接DM,在△ABD和△AMD中,∵,∴△ABD≌△AMD(SAS),∴MD=BD=CD ,过点M作MN∥AD,交EG于点N,交DE于点K.∵MN∥AD,∴,∴CK=CD,∴KD=CD,∴MD=KD,△DMK为等腰三角形,∴∠DMK=∠DKM,由题意得△EDG为等腰三角形,∠1=∠2,∵MN∥AD,∴∠3=∠4=∠1=∠2,又∵∠DKM=∠DMK=∠3,∴∠DMK=∠4,∴DM∥GN,∴四边形DMNG为平行四边形,∴MN=DG=2FD,∵点H为AC的中点,AC=AM,CM=AC,∴,∵MN∥AD,∴,即,∴.
赏析:本题主要采用构造法,构造全等三角形,平行四边形与等腰三角形;还用到了面积法,如用面积法得到BD=CD;还有转化法,将有关线段、比例线段多次转化,最终求得结果.本题是三角形的综合题,每一种方法都是解题关键,特别是有关线段、比例线段的多次转化,极易出错,解题一定要仔细.
易错题3:在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A、C重合),且∠ABP=30°,则CP的长为____________________.
答案:6或2或4
解答:如图1,当∠C=60°时,∠ABC=30°,点P在AC上或AC的延长线上时,这与∠ABP=30°相矛盾,此情况舍去;
如图2,当∠C=60°时,∠ABC=30°,点P在CA的延长线上时,∵∠ABP=30°,∴△ABC≌△ABP(ASA),∴∠CBP=∠ABC+∠ABP=30°+30°=60°,BC=BP,∴△PBC为等边三角形,∴CP=BC=6;21*cnjy*com
如图3,当∠ABC=60°时,∠C=30°,点P在AC上时,∵∠ABP=30°,∴∠PBC=∠ABC-∠ABP=60°-30°=30°,∴∠PBC=∠C,∴PC=PB,∵BC=6,∴AB=BC=3,∴PC=PB====2;
如图4,当∠ABC=60°时,∠C=30°,点P在CA的延长线上时,∵∠ABP=30°,∴∠PBC=∠ABC+∠ABP=60°+30°=90°,∴在Rt△PBC中,PC===4. 【来源:21cnj*y.co*m】
当∠ABC=60°时,∠C=30°,点P在AC的延长线上时,这与∠ABP=30°相矛盾,此情况舍去.【版权所有:21教育】
赏析:本题主要采用分类讨论法与数形结合法.由于题目中的两个条件信息不够明确,所以应分类讨论:一是条件“有一个锐角为60°”,应分∠ACB=60°和∠ABC=60°两种情况;二是条件“点P在直线AC上(不与点A、C重合)”,应分点P在AC上、点P在AC的延长线上与点P在CA的延长线上三种情况.
易错题4:如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角顶点重合于对角线BD上一点,EF、GH分别是折痕(如图2),设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的是____________________________.(写出所有正确判断的序号)
答案:①④
解答:对于①:当x=1时,观察图形,BE=AB-AE=2-x=2-1=1,由正方形的性质可得四边形BEFP也是正方形,∴BD=AB=2,BP=BE=,∴BP=BD,∴点P是正方形ABCD的中心,①正确;当x=时,则BE=2-=,AE=PG=1,又观察图形得四边形PHDG也是正方形,∴EF=BE=,GH=PG=,∴EF+GH=+=2,又∵AC=AB=2,∴EF+GH=AC,②错误; 对于③:当0<x<2时,设六边形AEFCHG面积为S,∵AB=2,AE=x,∴BE=BF=2-x,DG=DH=x,∴S=S正方形ABCD-S△BEF-S△GDH=2×2―(2-x)2―x2=﹣(x-1)2+3,当x=1时,S最大值=3,∴当x=1时,六边形AEFCHG面积的最大值是3,③错误;④当0<x<2时,设六边形AEFCHG周长为m,观察图形得m=AE+EF+FC+CH+HG+GA=AE+BP+FC+BF+PD+BE=AB+BC+BD=4+2,∴当0<x<2时,六边形AEFCHG周长的值不变,④正确.21教育网
赏析:本题主要采用了函数模型法和数形结合法.对于③④,分别建立二次函数与常数函数模型来求解,而每一结论都要通过观察图形,特别是图形中的正方形,矩形,等腰直角三角形,将一些相等的线段进行等量转换,使问题得以解决.
易错题5:如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在 BC上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是______________________.2-1-c-n-j-y
答案:①③⑤
解答:对于①:如图1,连接CD,∵点E与点D关于AC对称,∴CE=CD,∴∠E=∠CDE,∵DF⊥DE,∴∠EDF=90°,∴∠E+∠F=90°,∠CDE+∠CDF=90°,∴∠F=∠CDF,∴CE=CD=CF,∴①正确;21·世纪*教育网
对于②:如图2,当CD⊥AB时,∵AB是半圆的直径,∴∠ACB=90°,∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=4,∵CD⊥AB,∠CBA=30°,∴CD=BC=2,由“垂线段最短”得点D在AB上运动时,CD的最小值为2,∵CE=CD=CF,∴线段EF的最小值为4,∴②错误;
对于③:如图3,当AD=2时,连接OC,∵OA=OC,∠CAB=60°,∴△OAC是等边三角形,∴CA=CO,∠ACO=60°,∵AO=4,AD=2,∴DO=2,∴AD=DO,∴∠ACD=∠DCO=30°,∵点E与点D关于AC对称,∴∠ECA=∠DCA,∴∠ECA=30°,∴∠ECO=90°,∴OC⊥EF,∵EF经过半径OC外端,且OC⊥EF,∴EF与半圆相切,∴③正确;21cnjy.com
对于④:如图4,当点F恰好落在BC上时,连接FB、AF,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴,∵FC=EF,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∵BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=AB=4,∵DB=4,∴AD=AB-DB=4,∴④错误;
对于⑤:如图5,∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称,∴EF扫过的图形就是图5中的阴影部分,∴S阴影=2S△ABC=2××AC×BC=AC×BC=4×4=16,∴当点D从点A运动到点B时,线段EF扫过的面积是16,∴⑤正确.21教育名师原创作品
赏析:本题主要运用了直接求解法,构造法,运动轨迹法与面积法.这是一道圆的综合题,它综合了直角三角形,等边三角形,相似三角形,圆周角定理,圆的切线的判定,三角形面积的求法,轴对称等内容,轴对称性在本题中起着重要的作用,特别是⑤中轴对称性的运用是解决此问的关键.
易错练
1.如图,B为双曲线y=(x>0)上一点,直线AB∥y轴交直线y=x于点A,若OB2-AB2=12,则k=_______________.
2.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是______________________.
3.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=,DE交AC于点E,且cos=,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或;④0<CE≤6.4.其中正确的结论是___________________________.(填序号)
4.如图,在边长为6的正方形ABCD中,E是BC边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH,若BH=8,则FG=_____________.
5.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是__________________.
参考答案
易错练
1.6 赏析:如下图,延长AB交x轴于点C,设点C的横坐标为a,则点B的纵坐标为,点A的纵坐标为a,∴AB=a-.∵AB∥y轴,∴AC⊥OC.在Rt△BOC中,OB2=OC2+BC2=a2+()2,∵OB2-AB2=12,∴a2+()2-(a-)2=12,解得k=12.
2.﹣2<k< 赏析:由图可知,∠AOB=45°,∴直线OA的解析式为y=x.联立两个解析式得,消去y得x2-2x+2k=0,当△=b2-4ac=(﹣2)2-4×1×2k=0,即k=时,抛物线与OA有一个交点,此交点横坐标为1.∵点B的坐标为(2,0),∴OA=2,如下图,过点A作AC⊥OB于点C,则OC=CA=OAcos45°=2×=,∴点A的坐标为(,),交点在线段OA上;当抛物线经过点B(2,0)时,×22+k=0,解得k=﹣2.∴要使抛物线y=x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k<.21·cn·jy·com
3.①②③④ 赏析:对于①:∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B,∴∠ADE=∠C,∴△ADE∽△ACD,∴①正确;对于②:如下图,过点A作AF⊥BC于点F,∵AB=AC=
△DCE(ASA),∴②正确;对于③:当∠CED=90°时,则∠AED=90°,由①知,△ADE∽△ACD,∴∠ADC=∠AED,∵∠AED=90°,∴∠ADC=90°,即AD⊥BC,∵AB=AC,∴BD=CD,∴∠ADE=∠B=,cos=,AB=10,BD=8.当∠CDE=90°时,易证△CDE∽△BAD,∵∠CDE=90°,∴∠BAD=90°,∵∠B=,cos=,AB=10,∴cos∠B==,AB=10,∴BD=,∴③正确;对于④:易证△CDE∽△BAD,由①可知,BC=6,设BD=y,CE=x,∴,∴,∴y2-16y+64=64-10x,即(y-8)2=64-10x,∴64-10x≥0,解得x≤6.4,∴0<x≤6.4,∴④正确.
4.5 赏析:如图,连接CG,在△CGD与△CEB中,∵,∴△CGD≌△CEB(SAS),∴CG=CE,∠GCD=∠ECB,∴∠GCE=90°,即△GCE是等腰直角三角形.又∵CH⊥GE,∴CH=EH=GH.过点H作HM⊥AB于点M,HN⊥BC于点N,则∠MHN=90°,∴∠1=∠2,∴∠HEM=∠HCN.在△HEM与△HCN中,∵,∴△HEM≌△HCN(ASA),∴HM=HN,∴四边形MBNH是正方形.∵AH=8,∴BN=HN=4,∴CN=BC-BN=6-4=2.在Rt△HCN中,由勾股定理得CH=2,∴GH=CH=2,∵HM∥AG,∴∠1=∠3,∴∠2=∠3,又∵∠HNC=∠GHF=90°,∴Rt△HCN∽Rt△GFH,∴,∴,∴FG=5.www-2-1-cnjy-com
5.2≤AD<3 赏析:以D为圆心,AD长为半径画圆.①如图1,当圆与BC相切时,DE⊥BC.∵∠ABC=30°,∴DE=BD,∵AB=6,AD=DE,∴AD=2;②如图2,当圆与BC相交时,若交点为B或C时,都有AD=AB=3.∴AD的取值范围是2≤AD<3.
同课章节目录
