苏科版九年级数学下册试题 6.5相似三角形的性质(含答案)
文档属性
| 名称 | 苏科版九年级数学下册试题 6.5相似三角形的性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 257.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 15:26:36 | ||
图片预览


文档简介
6.5相似三角形的性质
一.选择题
1.如图,在△ABC中,DE∥BC,,记△ADE的面积为S1,四边形DBCE的面积为S2,则的值是( )
A. B. C. D.
2.下列结论正确的个数是( )
(1)一个多边形的内角和是外角和的3倍,则这个多边形是六边形;
(2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5;
(3)若△ABC∽△DEF,相似比为1:4,则S△ABC:S△DEF=1:4;
(4)若等腰三角形一个角为80°,则底角为80°或50°.
A.1 B.2 C.3 D.4
3.如图,在平行四边形中,E、F分别是AD、BC的中点,AC分别交BE、DF于G、H,下列结论:①BE=DF;②AG=GH=HC;③EGDH;④S△ABE=3S△AGE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
4.如图,D、E分别是△ABC的边AB、AC的中点,若△ADE的面积为1,则四边形DECB的面积为( )
A.2 B.3 C.4 D.6
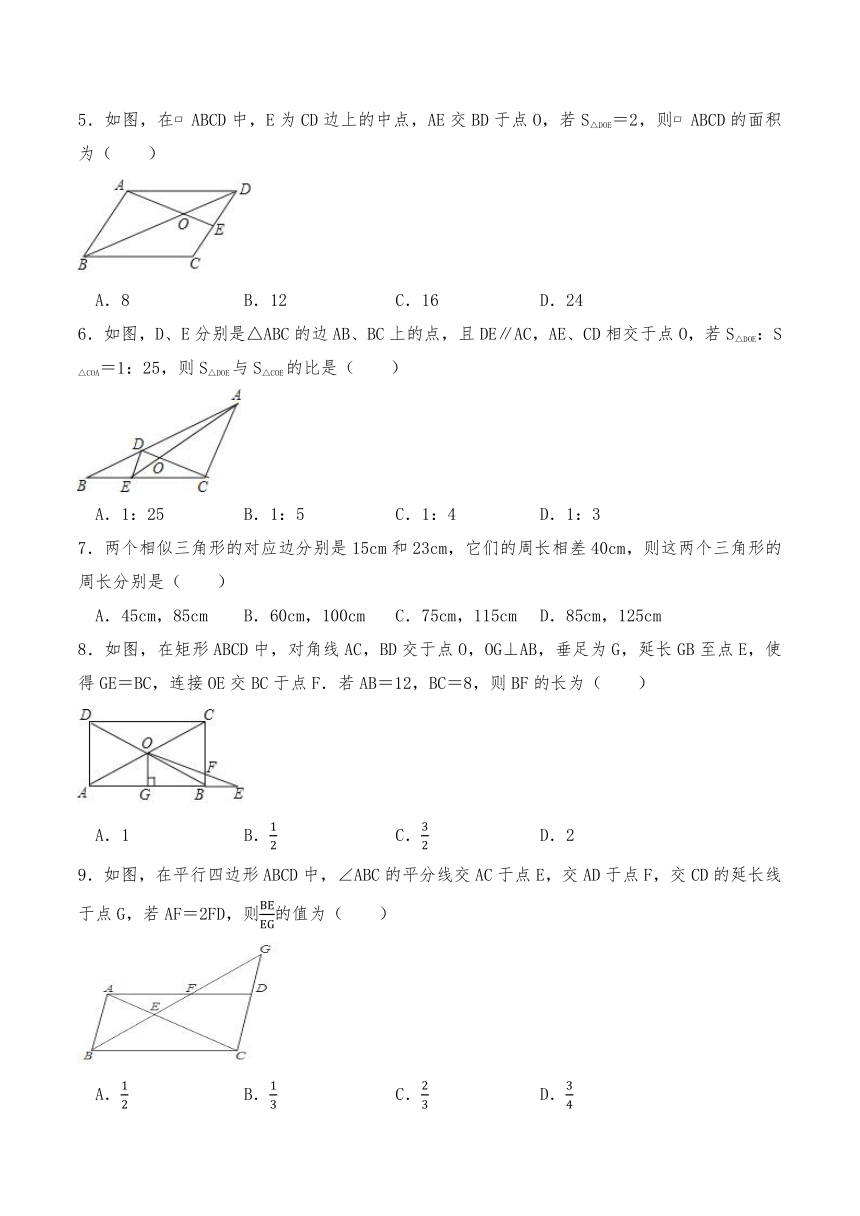
5.如图,在 ABCD中,E为CD边上的中点,AE交BD于点O,若S△DOE=2,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
6.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△DOE与S△COE的比是( )
A.1:25 B.1:5 C.1:4 D.1:3
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm B.60cm,100cm C.75cm,115cm D.85cm,125cm
8.如图,在矩形ABCD中,对角线AC,BD交于点O,OG⊥AB,垂足为G,延长GB至点E,使得GE=BC,连接OE交BC于点F.若AB=12,BC=8,则BF的长为( )
A.1 B. C. D.2
9.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
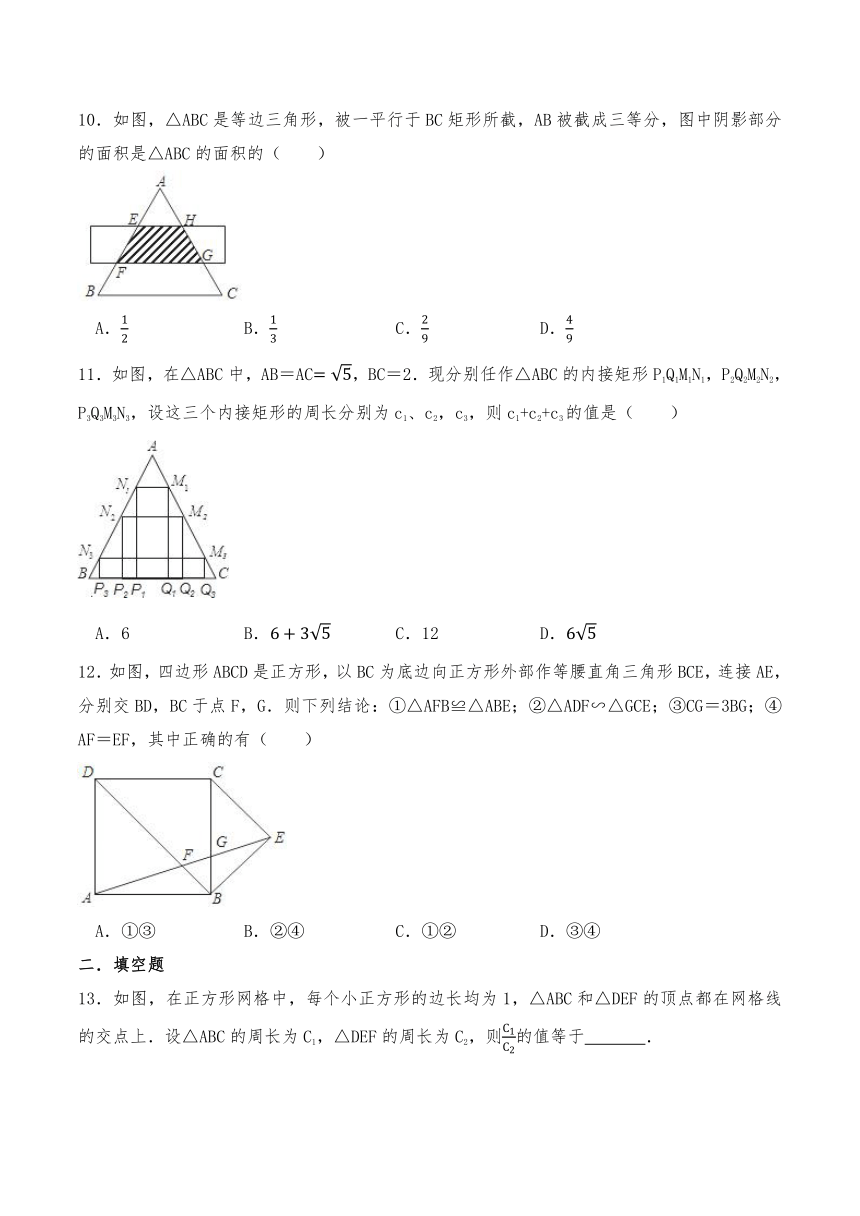
10.如图,△ABC是等边三角形,被一平行于BC矩形所截,AB被截成三等分,图中阴影部分的面积是△ABC的面积的( )
A. B. C. D.
11.如图,在△ABC中,AB=AC,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A.6 B. C.12 D.
12.如图,四边形ABCD是正方形,以BC为底边向正方形外部作等腰直角三角形BCE,连接AE,分别交BD,BC于点F,G.则下列结论:①△AFB≌△ABE;②△ADF∽△GCE;③CG=3BG;④AF=EF,其中正确的有( )
A.①③ B.②④ C.①② D.③④
二.填空题
13.如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .
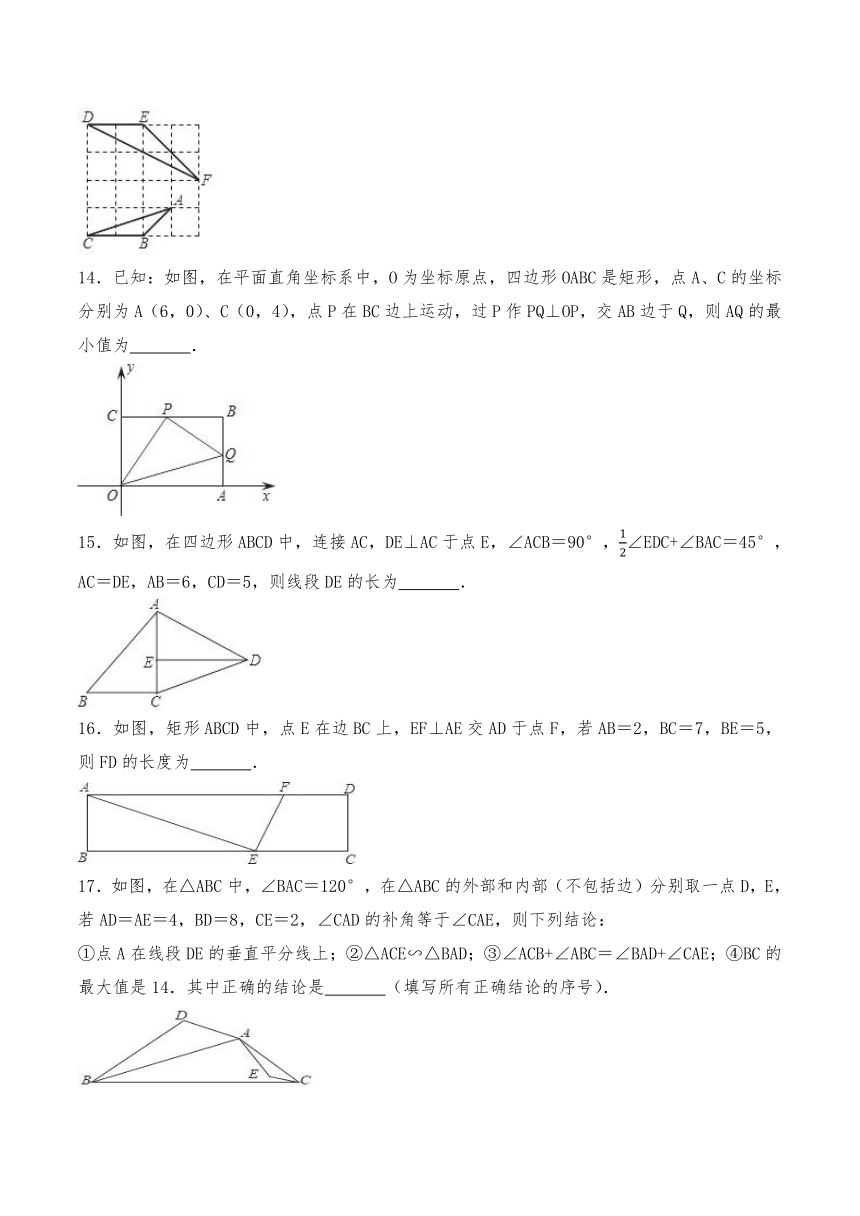
14.已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为 .
15.如图,在四边形ABCD中,连接AC,DE⊥AC于点E,∠ACB=90°,∠EDC+∠BAC=45°,AC=DE,AB=6,CD=5,则线段DE的长为 .
16.如图,矩形ABCD中,点E在边BC上,EF⊥AE交AD于点F,若AB=2,BC=7,BE=5,则FD的长度为 .
17.如图,在△ABC中,∠BAC=120°,在△ABC的外部和内部(不包括边)分别取一点D,E,若AD=AE=4,BD=8,CE=2,∠CAD的补角等于∠CAE,则下列结论:
①点A在线段DE的垂直平分线上;②△ACE∽△BAD;③∠ACB+∠ABC=∠BAD+∠CAE;④BC的最大值是14.其中正确的结论是 (填写所有正确结论的序号).
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=20,点M是AB的中点,点N是AC的中点,连接MN,点P是边BC上一点,PC=17,点Q是线段PC上的一个动点,连接MQ,PN,MQ与PN相交于点R.若△PQR是直角三角形,则MR的长是 .
19.如图,在矩形ABCD中,AB=4,BC=6,点E为对角线BD的中点,点F在CB的延长线上,且BF=1,连接EF,过点E作EG⊥EF交BA的延长线于点G,连接GF并延长交DB的延长线于点H,则 .
20.如图,等边三角形ABC中,AB=3,点D是CB延长线上一点,且BD=1,点E在直线AC上,当∠BAD=∠CDE时,AE的长为 .
21.已知:如图,正方形ABCD的边长为,∠EAF为∠BAD内的一个动角,两边分别交正方形的两个外角平分线于点E、F,且满足∠EAF=45°,连接EF、EC、CF,则BE DF= .
22.如图,在△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△ABM∽△ACN;③;④△PMN为等边三角形;⑤当∠ABC=45°时,BNPC.
其中正确的是 .(请填序号)
三.解答题
23.如图,在矩形ABCD中,已知AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)求证:△AEF∽△DCE.
(2)若AB=3,AE=4,DE=6,求线段BF的长.
24.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,.
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
25.如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
27.阅读与思考:
阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿下面是《阿基米德全集》中记载的一个命题:AB是⊙O的弦,点C在⊙O上,且CD⊥AB于点D,在弦AB上取点E,使AD=DE,点F是上的一点,且,连接BF可得BF=BE.
(1)将上述问题中弦AB改为直径AB,如图1所示,试证明BF=BE;
(2)如图2所示,若直径AB=10,EOOB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
28.如图,BD、CE是△ABC的高.
(1)求证:△ACE∽△ABD;
(2)若BD=8,AD=6,DE=5,求BC的长.
29.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ABE=∠C.
(1)求证:BE2=DE BC;
(2)当BE平分∠ABC时,求证:.
30.如图1,在菱形ABCD中,AC=2,BD=2,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
31.如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
答案
一.选择题
A.B.D.B.D.B.C.A.C.B.C.B.
二.填空题
13..
14..
15..
16..
17.①③.
18.或.
19..
20.2或.
21.3.
22.①②③④⑤.
三.解答题
23.(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠F=90°
∵EF⊥CE,
∴∠CED+∠AEF=180°﹣90°=90°,
∴∠CED=∠F,又∵∠A=∠D=90°,
∴△AFE∽△DEC.
(2)∵△AFE∽△DEC,
∴,
∵AB=CD=3,AE=4,DE=6,
∴,
解得BF=5.
答:线段BF的长为5.
24.证明:(1)∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
∵
∴,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)∵∠B=∠C,
∴AB=AC=3,且CD=2,
∴AD=1,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴
∴AP2=1×3=3
∴AP.
25.(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,
∵∠BEF=90°,
∵∠ABE+∠EBA=∠DEF+∠EBA=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)解:∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3,
∵△ABE∽△DEF,
∴,即,
解得:DE=2,
∵AD∥BC,
∴△EDF∽△GCF,
∴,即,
∴CG=6,
∴BG=BC+CG=4+6=10.
26.解:(1)∵CD⊥AB于D,BE⊥AC于E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE∽△ACD;
(2)∵△ABE∽△ACD,
∴,
在△ADE和△ACB中,
,
∴△ADE∽△ACB,
∴,
∴AD BC=DE AC.
27.解:(1)如图1所示,连接CE、BC,
∵CD⊥AB,AD=DE,
∴AC=CE,
∴∠CAE=∠CEA,
又∵,
∴CA=CF,∠FBC=∠EBC,
∴CE=CF,
又∵∠A+∠F=180°,∠CEA+∠CEB=180°,
∴∠CEB=∠F,
∴△CEB≌△CFB(AAS),
∴BE=BF;
(2)如图2所示,连接AF,
∵AB=10,EO,
∴EB=7.5,
∵AB为⊙O的直径,
∴∠AFB=90°,
∵l与与⊙O相切于点F,
∴∠OFP=90°,
∴∠AFO=∠BFP,
又∵OF=OA,
∴∠OAF=∠OFA,
∴∠OAF=∠BFP,
∵BP⊥l于点P,
∴∠BPF=90°,
∴△AFB∽△FPB,
∴,
即,
∴.
28.解:(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ACE∽△ABD;
(2)在Rt△ABD中,BD=8,AD=6,
根据勾股定理,得
AB10,
∵△ACE∽△ABD,
∴,
∵∠A=∠A,
∴△AED∽△ACB,
∴,
∵DE=5,
∴BC.
29.证明:(1)∵DE∥BC,
∴∠BED=∠CBE,
又∵∠ABE=∠C,
∴△BDE∽△CEB,
∴,
∴BE2=DE BC.
(2)∵DE∥BC,
∴∠AED=∠C.又∠ABE=∠C,
∴∠AED=∠ABE,
又∵∠EAD=∠BAE,
∴△ADE∽△AEB,
∴,
∵DE∥BC,
∴,即,
∴,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵∠ABE=∠C,
∴∠CBE=∠C,
∴BE=CE,
∴.
30.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,
∴△AOB为直角三角形,且OAAC=1,OBBD.
在Rt△AOB中,由勾股定理得:
AB2.
(2)①△AEF是等边三角形.理由如下:
∵由(1)知,菱形边长为2,AC=2,
∴△ABC与△ACD均为等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
又∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
∵,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF是等腰三角形,
又∵∠EAF=60°,
∴△AEF是等边三角形.
②BC=2,E为四等分点,且BE>CE,
∴CE,BE.
由①知△ABE≌△ACF,
∴CF=BE.
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),
∠EGA=∠CGF(对顶角)
∴∠EAC=∠GFC.
在△CAE与△CFG中,
∵,
∴△CAE∽△CFG,
∴,即,
解得:CG.
31.解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE,
∴EF,
∴CF=EF﹣EC1;
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴△EGC∽△GFC,
∴,
∵GC=a,FC=2a,
∴,
∴,
∴ECa,BE=BC﹣EC=2aaa,
∴λ.
一.选择题
1.如图,在△ABC中,DE∥BC,,记△ADE的面积为S1,四边形DBCE的面积为S2,则的值是( )
A. B. C. D.
2.下列结论正确的个数是( )
(1)一个多边形的内角和是外角和的3倍,则这个多边形是六边形;
(2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5;
(3)若△ABC∽△DEF,相似比为1:4,则S△ABC:S△DEF=1:4;
(4)若等腰三角形一个角为80°,则底角为80°或50°.
A.1 B.2 C.3 D.4
3.如图,在平行四边形中,E、F分别是AD、BC的中点,AC分别交BE、DF于G、H,下列结论:①BE=DF;②AG=GH=HC;③EGDH;④S△ABE=3S△AGE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
4.如图,D、E分别是△ABC的边AB、AC的中点,若△ADE的面积为1,则四边形DECB的面积为( )
A.2 B.3 C.4 D.6
5.如图,在 ABCD中,E为CD边上的中点,AE交BD于点O,若S△DOE=2,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
6.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△DOE与S△COE的比是( )
A.1:25 B.1:5 C.1:4 D.1:3
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm B.60cm,100cm C.75cm,115cm D.85cm,125cm
8.如图,在矩形ABCD中,对角线AC,BD交于点O,OG⊥AB,垂足为G,延长GB至点E,使得GE=BC,连接OE交BC于点F.若AB=12,BC=8,则BF的长为( )
A.1 B. C. D.2
9.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
10.如图,△ABC是等边三角形,被一平行于BC矩形所截,AB被截成三等分,图中阴影部分的面积是△ABC的面积的( )
A. B. C. D.
11.如图,在△ABC中,AB=AC,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A.6 B. C.12 D.
12.如图,四边形ABCD是正方形,以BC为底边向正方形外部作等腰直角三角形BCE,连接AE,分别交BD,BC于点F,G.则下列结论:①△AFB≌△ABE;②△ADF∽△GCE;③CG=3BG;④AF=EF,其中正确的有( )
A.①③ B.②④ C.①② D.③④
二.填空题
13.如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .
14.已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为 .
15.如图,在四边形ABCD中,连接AC,DE⊥AC于点E,∠ACB=90°,∠EDC+∠BAC=45°,AC=DE,AB=6,CD=5,则线段DE的长为 .
16.如图,矩形ABCD中,点E在边BC上,EF⊥AE交AD于点F,若AB=2,BC=7,BE=5,则FD的长度为 .
17.如图,在△ABC中,∠BAC=120°,在△ABC的外部和内部(不包括边)分别取一点D,E,若AD=AE=4,BD=8,CE=2,∠CAD的补角等于∠CAE,则下列结论:
①点A在线段DE的垂直平分线上;②△ACE∽△BAD;③∠ACB+∠ABC=∠BAD+∠CAE;④BC的最大值是14.其中正确的结论是 (填写所有正确结论的序号).
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=20,点M是AB的中点,点N是AC的中点,连接MN,点P是边BC上一点,PC=17,点Q是线段PC上的一个动点,连接MQ,PN,MQ与PN相交于点R.若△PQR是直角三角形,则MR的长是 .
19.如图,在矩形ABCD中,AB=4,BC=6,点E为对角线BD的中点,点F在CB的延长线上,且BF=1,连接EF,过点E作EG⊥EF交BA的延长线于点G,连接GF并延长交DB的延长线于点H,则 .
20.如图,等边三角形ABC中,AB=3,点D是CB延长线上一点,且BD=1,点E在直线AC上,当∠BAD=∠CDE时,AE的长为 .
21.已知:如图,正方形ABCD的边长为,∠EAF为∠BAD内的一个动角,两边分别交正方形的两个外角平分线于点E、F,且满足∠EAF=45°,连接EF、EC、CF,则BE DF= .
22.如图,在△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△ABM∽△ACN;③;④△PMN为等边三角形;⑤当∠ABC=45°时,BNPC.
其中正确的是 .(请填序号)
三.解答题
23.如图,在矩形ABCD中,已知AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)求证:△AEF∽△DCE.
(2)若AB=3,AE=4,DE=6,求线段BF的长.
24.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,.
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
25.如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
27.阅读与思考:
阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿下面是《阿基米德全集》中记载的一个命题:AB是⊙O的弦,点C在⊙O上,且CD⊥AB于点D,在弦AB上取点E,使AD=DE,点F是上的一点,且,连接BF可得BF=BE.
(1)将上述问题中弦AB改为直径AB,如图1所示,试证明BF=BE;
(2)如图2所示,若直径AB=10,EOOB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
28.如图,BD、CE是△ABC的高.
(1)求证:△ACE∽△ABD;
(2)若BD=8,AD=6,DE=5,求BC的长.
29.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ABE=∠C.
(1)求证:BE2=DE BC;
(2)当BE平分∠ABC时,求证:.
30.如图1,在菱形ABCD中,AC=2,BD=2,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
31.如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
答案
一.选择题
A.B.D.B.D.B.C.A.C.B.C.B.
二.填空题
13..
14..
15..
16..
17.①③.
18.或.
19..
20.2或.
21.3.
22.①②③④⑤.
三.解答题
23.(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠F=90°
∵EF⊥CE,
∴∠CED+∠AEF=180°﹣90°=90°,
∴∠CED=∠F,又∵∠A=∠D=90°,
∴△AFE∽△DEC.
(2)∵△AFE∽△DEC,
∴,
∵AB=CD=3,AE=4,DE=6,
∴,
解得BF=5.
答:线段BF的长为5.
24.证明:(1)∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
∵
∴,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)∵∠B=∠C,
∴AB=AC=3,且CD=2,
∴AD=1,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴
∴AP2=1×3=3
∴AP.
25.(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,
∵∠BEF=90°,
∵∠ABE+∠EBA=∠DEF+∠EBA=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)解:∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3,
∵△ABE∽△DEF,
∴,即,
解得:DE=2,
∵AD∥BC,
∴△EDF∽△GCF,
∴,即,
∴CG=6,
∴BG=BC+CG=4+6=10.
26.解:(1)∵CD⊥AB于D,BE⊥AC于E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE∽△ACD;
(2)∵△ABE∽△ACD,
∴,
在△ADE和△ACB中,
,
∴△ADE∽△ACB,
∴,
∴AD BC=DE AC.
27.解:(1)如图1所示,连接CE、BC,
∵CD⊥AB,AD=DE,
∴AC=CE,
∴∠CAE=∠CEA,
又∵,
∴CA=CF,∠FBC=∠EBC,
∴CE=CF,
又∵∠A+∠F=180°,∠CEA+∠CEB=180°,
∴∠CEB=∠F,
∴△CEB≌△CFB(AAS),
∴BE=BF;
(2)如图2所示,连接AF,
∵AB=10,EO,
∴EB=7.5,
∵AB为⊙O的直径,
∴∠AFB=90°,
∵l与与⊙O相切于点F,
∴∠OFP=90°,
∴∠AFO=∠BFP,
又∵OF=OA,
∴∠OAF=∠OFA,
∴∠OAF=∠BFP,
∵BP⊥l于点P,
∴∠BPF=90°,
∴△AFB∽△FPB,
∴,
即,
∴.
28.解:(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ACE∽△ABD;
(2)在Rt△ABD中,BD=8,AD=6,
根据勾股定理,得
AB10,
∵△ACE∽△ABD,
∴,
∵∠A=∠A,
∴△AED∽△ACB,
∴,
∵DE=5,
∴BC.
29.证明:(1)∵DE∥BC,
∴∠BED=∠CBE,
又∵∠ABE=∠C,
∴△BDE∽△CEB,
∴,
∴BE2=DE BC.
(2)∵DE∥BC,
∴∠AED=∠C.又∠ABE=∠C,
∴∠AED=∠ABE,
又∵∠EAD=∠BAE,
∴△ADE∽△AEB,
∴,
∵DE∥BC,
∴,即,
∴,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵∠ABE=∠C,
∴∠CBE=∠C,
∴BE=CE,
∴.
30.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,
∴△AOB为直角三角形,且OAAC=1,OBBD.
在Rt△AOB中,由勾股定理得:
AB2.
(2)①△AEF是等边三角形.理由如下:
∵由(1)知,菱形边长为2,AC=2,
∴△ABC与△ACD均为等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
又∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
∵,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF是等腰三角形,
又∵∠EAF=60°,
∴△AEF是等边三角形.
②BC=2,E为四等分点,且BE>CE,
∴CE,BE.
由①知△ABE≌△ACF,
∴CF=BE.
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),
∠EGA=∠CGF(对顶角)
∴∠EAC=∠GFC.
在△CAE与△CFG中,
∵,
∴△CAE∽△CFG,
∴,即,
解得:CG.
31.解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE,
∴EF,
∴CF=EF﹣EC1;
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴△EGC∽△GFC,
∴,
∵GC=a,FC=2a,
∴,
∴,
∴ECa,BE=BC﹣EC=2aaa,
∴λ.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
