苏科版九年级数学下册试题 8.6收取多少保险费才合理(含答案)
文档属性
| 名称 | 苏科版九年级数学下册试题 8.6收取多少保险费才合理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 15:30:55 | ||
图片预览




文档简介
8.6收取多少保险费才合理
一.选择题
1.如图,一个可以自由转动的转盘,被分成了6个相同的扇形,转动转盘,转盘停止时,指针落在白色区域的概率等于( )
A. B. C. D.无法确定
2.在不透明的袋中有5个白球,3个黑球,除颜色外均相同.从中任意摸出一个球,则摸到黑球的概率是( )
A. B. C. D.
3.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
4.某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图所示),并规定:顾客消费200元以上(含200元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分界线上时,则需要重新转动转盘.某顾客正好消费300元,他转动一次转盘,实际付款210元的概率为( )
A. B. C. D.
5.一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为( )
A. B. C. D.
6.如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )
A. B. C. D.
7.在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
8.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格的形状大小质地完全相同,当蚂蚁停下来时,停在地板中阴影部分的概率是( )
A. B. C. D.
9.如图是一个是圆形房间的地板图案,其中大圆的直径恰好等于两个小圆的直径的和(两个小圆的直径相等),若在房间内任意扔一颗小玻璃珠,则小玻璃珠静止后,滚落在阴影部分的概率是( )
A. B. C. D.
10.一个布袋里装有2个红球、3个黄球和5个白球,除颜色外其它都相同.搅匀后任意摸出一个球,是黄球的概率为( )
A. B. C. D.
11.如图,转盘的红、黄、蓝、紫四个扇形区域的圆心角分别记为α,β,γ,θ.自由转动转盘,则下面说法错误的是( )
A.若α>90°,则指针落在红色区域的概率大于0.25
B.若α>β+γ+θ,则指针落在红色区域的概率大于0.5
C.若α﹣β=γ﹣θ,则指针落在红色或黄色区域的概率和为0.5
D.若γ+θ=180°,则指针落在红色或黄色区域的概率和为0.5
12.正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区域的概率是( )
A. B. C. D.
二.填空题
13.有6张卡片,上面分别标有0,1,2,3,4,5这6个数字,将它们背面洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的分式方程2的解为正数,且使关于y的不等式组的解集为y<﹣2,则抽到符合条件的a的概率为 .
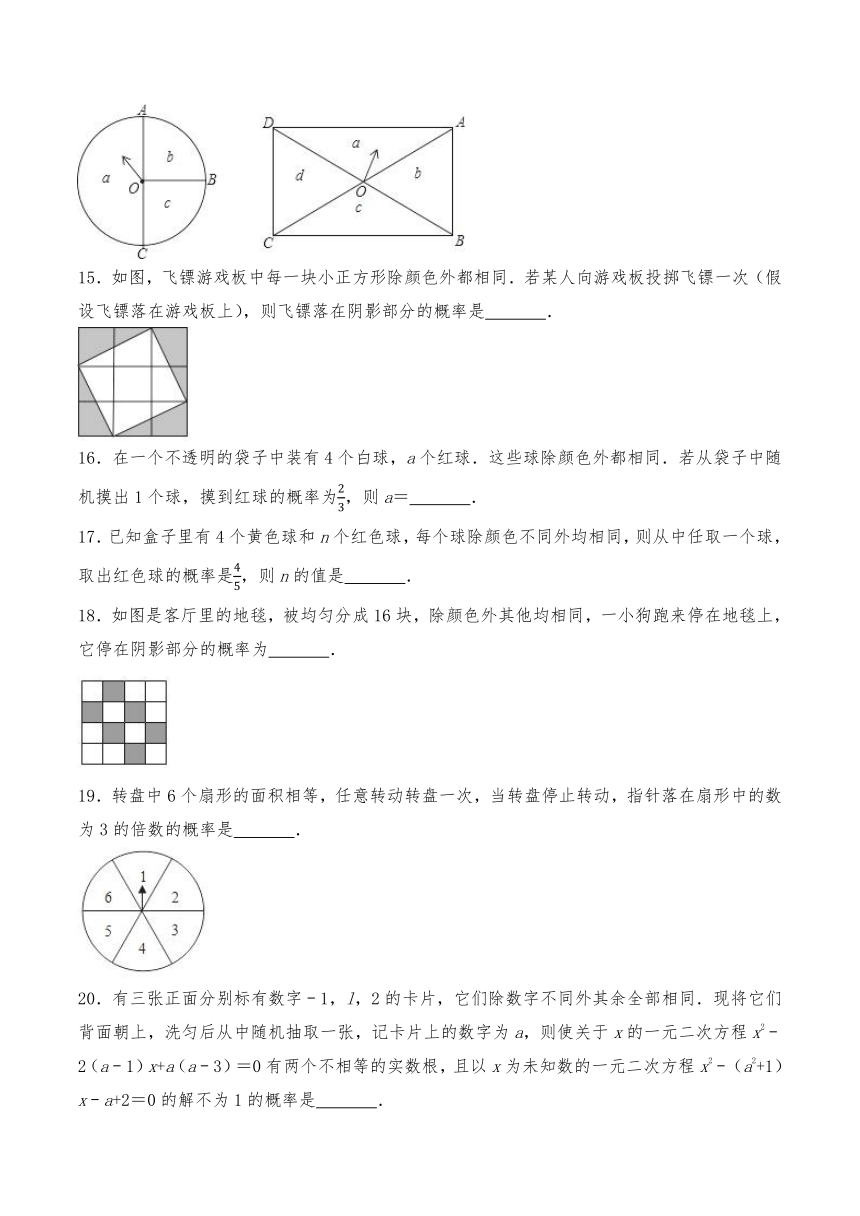
14.如图所示,在圆形转盘中,∠AOB=∠BOC=90°,拨动指针,指针指向区域a的概率为P1,在矩形转盘中,CD=1,BD=2,拨动指针,指针指向a区域的概率为P2,则P1+P2= .
15.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是 .
16.在一个不透明的袋子中装有4个白球,a个红球.这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到红球的概率为,则a= .
17.已知盒子里有4个黄色球和n个红色球,每个球除颜色不同外均相同,则从中任取一个球,取出红色球的概率是,则n的值是 .
18.如图是客厅里的地毯,被均匀分成16块,除颜色外其他均相同,一小狗跑来停在地毯上,它停在阴影部分的概率为 .
19.转盘中6个扇形的面积相等,任意转动转盘一次,当转盘停止转动,指针落在扇形中的数为3的倍数的概率是 .
20.有三张正面分别标有数字﹣1,l,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2﹣(a2+1)x﹣a+2=0的解不为1的概率是 .
21.如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
22.二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是 .
23.已知菱形ABCD中,对角线AC=8cm,BD=6cm,在菱形内部(包括边界)任取一点P,得到△ACP并涂成黑色,使黑色部分的面积大于6cm2的概率为 .
24.有五张正面分别标有数0,1,2,3,4,5的不透明卡片,它们除了数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将卡片上的数记为a,则使关于x的方程2有正整数解的概率为
三.解答题
25.计算下列各题:
如图,是一个圆形转盘,现按1:2:3:4分成四个部分,分别涂上红、黄、蓝、绿四种颜色,自由转动转盘,请计算:
(1)停止后指针落在蓝色区域的概率;
(2)黄色区域扇形的圆心角度数是多少?
26.手机微信中的抢红包游戏有一种玩法为“拼手气红包”:用户设定好总金额以及红包个数之后,可以生成不等金额的红包.现有四个人组成的微信群中,其中一人发了三个“拼手气红包”,其他三人随机抢红包.
(1)若甲的速度最快,求甲抢到最多金额的红包的概率;
(2)若三个人同时点击红包,记金额最多、居中、最少的红包分别为A、B、C,试求出甲抢到红包A的概率P(A).
27.一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)判断摸到什么颜色的球可能性最大?
(2)求摸到黄颜色的球的概率;
(3)要使摸到这三种颜色的球的概率相等,需要在这个口袋里的球做什么调整?
28.一项答题竞猜活动,在6个式样、大小都相同的箱子中有且只有一个箱子里藏有礼物.参与选手将回答5道题目,每答对一道题,主持人就从6个箱子中去掉一个空箱子.而选手一旦答错,即取消后面的答题资格,从剩下的箱子中选取一个箱子.
(1)一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)已知一个选手选中藏有礼物的箱子的概率为,则他答对了几道题?
29.某家庭记录了未使用节水水龙头50天的日用水量数据(单位:m3)和使用了节水水龙头50天的日用水量数据(单位:m3),得到频数直方图如图:
(1)估计该家庭使用节水水龙头后,日用水量小于0.4m3的概率;
(2)为了计算方便,把用水量介于0﹣0.1m3之间的日用水量均近似的看做0.05m3,用水量介于0.1﹣0.2m3之间的日用水量均近似的看做0.15m3,用水量介于0.2﹣0.3m3之间的日用水量均近似的看做0.25m3,…,依此类推.请估计该家庭使用节水水龙头前后的日用水量分别是多少?(结果精确到0.01m3)
(3)如果一年按365天计算,那么利用(2)的结论估计该家庭一年能节省多少水?
30.随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) 0<x≤1 1<x≤2 2<x≤3 3<x≤4 4<x≤5
数量 12 20 24 16 8
(Ⅰ)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(Ⅱ)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(Ⅲ)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元.以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
答案
一.选择题
C.C.A.D.C.A.B.B.A.B.C.B.
二.填空题
13..
14..
15..
16.8.
17.16.
18..
19..
20..
21..
22.
23..
24..
三.解答题
25.解:(1)∵圆被等分成1+2+3+4=10份,其中蓝色部分占3份,
∴停止后指针落在蓝色区域的概率为:;
(2)360°=72°,
答:黄色区域扇形的圆心角度数是72°.
26.解:(1)因甲的速度最快,则甲抢到红包的可能性有三种,
因此甲抢到最多金额的红包的概率为;
(2)甲、乙、丙三人抢到的红包所有可能情况如下:
甲A、乙B、丙C;甲A、乙C、丙B;甲B、乙A、丙C;甲B、乙C、丙A;甲C、乙A、丙B;甲C、乙B、丙A;
共有6种可能,甲抢到红包A的可能性有2种,
所以甲抢到红包A的概率P(A).
27.解:(1)∵不透明的袋子中装有1个白球、2个黄球和3个红球,红球最多,
∴摸到红球的可能性最大;
(2)摸到黄颜色的球的概率是;
(3)要使摸到这三种颜色的球的概率相等,要把袋子里的1个红球变成白球即可.
28.解:(1)∵共6个箱子,答对了4道取走4个箱子,
∴还剩2个箱子,
∴一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)∵一个选手选中藏有礼物的箱子的概率为,
∴他从5个箱子中选择一个箱子,
∴则他答对了1道题;
29.解:(1)根据频数直方图可知:
该家庭使用节水水龙头后,日用水量小于0.4m3的概率约为:
P0.4.
答:该家庭使用节水水龙头后,日用水量小于0.4m3的概率约为0.4;
(2)未使用节水水龙头50天的日用水量为:
(2×0.05+4×0.15+4×0.25+6×0.35+10×0.45+16×0.55+8×0.65)
=0.446≈0.45,
使用节水水龙头50天的日用水量为:
(2×0.05+4×0.15+6×0.25+8×0.35+16×0.45+10×0.55+4×0.65)
=0.406≈0.41.
答:该家庭使用节水水龙头前后的日用水量分别是0.45m3,0.41m3;
(3)由(2)可知:
一年能节省水:365×(0.45﹣0.41)=14.6(m3),
答:该家庭一年能节省14.6m3的水.
30.解:(Ⅰ)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为:.
故答案为;
(Ⅱ)估计利用该平台点外卖用户的平均送餐距离为(12×0.5+20×1.5+24×2.5+16×3.5+8×4.5)=2.35(千米);
(Ⅲ)送一份外卖的平均收入为:359(元),
由15032.6,
所以估计一天至少要送33份外卖.
一.选择题
1.如图,一个可以自由转动的转盘,被分成了6个相同的扇形,转动转盘,转盘停止时,指针落在白色区域的概率等于( )
A. B. C. D.无法确定
2.在不透明的袋中有5个白球,3个黑球,除颜色外均相同.从中任意摸出一个球,则摸到黑球的概率是( )
A. B. C. D.
3.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
4.某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图所示),并规定:顾客消费200元以上(含200元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分界线上时,则需要重新转动转盘.某顾客正好消费300元,他转动一次转盘,实际付款210元的概率为( )
A. B. C. D.
5.一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为( )
A. B. C. D.
6.如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )
A. B. C. D.
7.在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
8.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格的形状大小质地完全相同,当蚂蚁停下来时,停在地板中阴影部分的概率是( )
A. B. C. D.
9.如图是一个是圆形房间的地板图案,其中大圆的直径恰好等于两个小圆的直径的和(两个小圆的直径相等),若在房间内任意扔一颗小玻璃珠,则小玻璃珠静止后,滚落在阴影部分的概率是( )
A. B. C. D.
10.一个布袋里装有2个红球、3个黄球和5个白球,除颜色外其它都相同.搅匀后任意摸出一个球,是黄球的概率为( )
A. B. C. D.
11.如图,转盘的红、黄、蓝、紫四个扇形区域的圆心角分别记为α,β,γ,θ.自由转动转盘,则下面说法错误的是( )
A.若α>90°,则指针落在红色区域的概率大于0.25
B.若α>β+γ+θ,则指针落在红色区域的概率大于0.5
C.若α﹣β=γ﹣θ,则指针落在红色或黄色区域的概率和为0.5
D.若γ+θ=180°,则指针落在红色或黄色区域的概率和为0.5
12.正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区域的概率是( )
A. B. C. D.
二.填空题
13.有6张卡片,上面分别标有0,1,2,3,4,5这6个数字,将它们背面洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的分式方程2的解为正数,且使关于y的不等式组的解集为y<﹣2,则抽到符合条件的a的概率为 .
14.如图所示,在圆形转盘中,∠AOB=∠BOC=90°,拨动指针,指针指向区域a的概率为P1,在矩形转盘中,CD=1,BD=2,拨动指针,指针指向a区域的概率为P2,则P1+P2= .
15.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是 .
16.在一个不透明的袋子中装有4个白球,a个红球.这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到红球的概率为,则a= .
17.已知盒子里有4个黄色球和n个红色球,每个球除颜色不同外均相同,则从中任取一个球,取出红色球的概率是,则n的值是 .
18.如图是客厅里的地毯,被均匀分成16块,除颜色外其他均相同,一小狗跑来停在地毯上,它停在阴影部分的概率为 .
19.转盘中6个扇形的面积相等,任意转动转盘一次,当转盘停止转动,指针落在扇形中的数为3的倍数的概率是 .
20.有三张正面分别标有数字﹣1,l,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2﹣(a2+1)x﹣a+2=0的解不为1的概率是 .
21.如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
22.二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是 .
23.已知菱形ABCD中,对角线AC=8cm,BD=6cm,在菱形内部(包括边界)任取一点P,得到△ACP并涂成黑色,使黑色部分的面积大于6cm2的概率为 .
24.有五张正面分别标有数0,1,2,3,4,5的不透明卡片,它们除了数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将卡片上的数记为a,则使关于x的方程2有正整数解的概率为
三.解答题
25.计算下列各题:
如图,是一个圆形转盘,现按1:2:3:4分成四个部分,分别涂上红、黄、蓝、绿四种颜色,自由转动转盘,请计算:
(1)停止后指针落在蓝色区域的概率;
(2)黄色区域扇形的圆心角度数是多少?
26.手机微信中的抢红包游戏有一种玩法为“拼手气红包”:用户设定好总金额以及红包个数之后,可以生成不等金额的红包.现有四个人组成的微信群中,其中一人发了三个“拼手气红包”,其他三人随机抢红包.
(1)若甲的速度最快,求甲抢到最多金额的红包的概率;
(2)若三个人同时点击红包,记金额最多、居中、最少的红包分别为A、B、C,试求出甲抢到红包A的概率P(A).
27.一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)判断摸到什么颜色的球可能性最大?
(2)求摸到黄颜色的球的概率;
(3)要使摸到这三种颜色的球的概率相等,需要在这个口袋里的球做什么调整?
28.一项答题竞猜活动,在6个式样、大小都相同的箱子中有且只有一个箱子里藏有礼物.参与选手将回答5道题目,每答对一道题,主持人就从6个箱子中去掉一个空箱子.而选手一旦答错,即取消后面的答题资格,从剩下的箱子中选取一个箱子.
(1)一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)已知一个选手选中藏有礼物的箱子的概率为,则他答对了几道题?
29.某家庭记录了未使用节水水龙头50天的日用水量数据(单位:m3)和使用了节水水龙头50天的日用水量数据(单位:m3),得到频数直方图如图:
(1)估计该家庭使用节水水龙头后,日用水量小于0.4m3的概率;
(2)为了计算方便,把用水量介于0﹣0.1m3之间的日用水量均近似的看做0.05m3,用水量介于0.1﹣0.2m3之间的日用水量均近似的看做0.15m3,用水量介于0.2﹣0.3m3之间的日用水量均近似的看做0.25m3,…,依此类推.请估计该家庭使用节水水龙头前后的日用水量分别是多少?(结果精确到0.01m3)
(3)如果一年按365天计算,那么利用(2)的结论估计该家庭一年能节省多少水?
30.随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) 0<x≤1 1<x≤2 2<x≤3 3<x≤4 4<x≤5
数量 12 20 24 16 8
(Ⅰ)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(Ⅱ)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(Ⅲ)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元.以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
答案
一.选择题
C.C.A.D.C.A.B.B.A.B.C.B.
二.填空题
13..
14..
15..
16.8.
17.16.
18..
19..
20..
21..
22.
23..
24..
三.解答题
25.解:(1)∵圆被等分成1+2+3+4=10份,其中蓝色部分占3份,
∴停止后指针落在蓝色区域的概率为:;
(2)360°=72°,
答:黄色区域扇形的圆心角度数是72°.
26.解:(1)因甲的速度最快,则甲抢到红包的可能性有三种,
因此甲抢到最多金额的红包的概率为;
(2)甲、乙、丙三人抢到的红包所有可能情况如下:
甲A、乙B、丙C;甲A、乙C、丙B;甲B、乙A、丙C;甲B、乙C、丙A;甲C、乙A、丙B;甲C、乙B、丙A;
共有6种可能,甲抢到红包A的可能性有2种,
所以甲抢到红包A的概率P(A).
27.解:(1)∵不透明的袋子中装有1个白球、2个黄球和3个红球,红球最多,
∴摸到红球的可能性最大;
(2)摸到黄颜色的球的概率是;
(3)要使摸到这三种颜色的球的概率相等,要把袋子里的1个红球变成白球即可.
28.解:(1)∵共6个箱子,答对了4道取走4个箱子,
∴还剩2个箱子,
∴一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)∵一个选手选中藏有礼物的箱子的概率为,
∴他从5个箱子中选择一个箱子,
∴则他答对了1道题;
29.解:(1)根据频数直方图可知:
该家庭使用节水水龙头后,日用水量小于0.4m3的概率约为:
P0.4.
答:该家庭使用节水水龙头后,日用水量小于0.4m3的概率约为0.4;
(2)未使用节水水龙头50天的日用水量为:
(2×0.05+4×0.15+4×0.25+6×0.35+10×0.45+16×0.55+8×0.65)
=0.446≈0.45,
使用节水水龙头50天的日用水量为:
(2×0.05+4×0.15+6×0.25+8×0.35+16×0.45+10×0.55+4×0.65)
=0.406≈0.41.
答:该家庭使用节水水龙头前后的日用水量分别是0.45m3,0.41m3;
(3)由(2)可知:
一年能节省水:365×(0.45﹣0.41)=14.6(m3),
答:该家庭一年能节省14.6m3的水.
30.解:(Ⅰ)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为:.
故答案为;
(Ⅱ)估计利用该平台点外卖用户的平均送餐距离为(12×0.5+20×1.5+24×2.5+16×3.5+8×4.5)=2.35(千米);
(Ⅲ)送一份外卖的平均收入为:359(元),
由15032.6,
所以估计一天至少要送33份外卖.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
