九年级数学下册试题 8.6收取多少保险费才合理同步练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 8.6收取多少保险费才合理同步练习-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 91.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 15:31:36 | ||
图片预览




文档简介
8.6收取多少保险费才合理
一.选择题
1. 一个不透明的盒子里装有红、黄、白三种颜色的球,个数分别为2、3、4,这些球除颜色外都相同,从盒子中任抽一个球,则抽到红球的概率是( )
A. B. C. D.
2. 在一个不透明的袋子里装有2个黑球3个白球,它们除颜色外都相同,随机从中摸出一个球,是黑球的概率是( )
A. B. C. D.
3. 从一副扑克牌中任意抽出1张牌,抽得下列牌中的概率最大的是( )
A.小王 B.大王 C.10 D.黑桃
4. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏:小明摸到的牌面是5(不放回),小颖从剩余的牌中抽取一张(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关),谁的牌面大谁就获胜.则小明获胜的概率是( )
A. B. C. D.
5. 如图,小亮有一个卡片藏在9块瓷砖中的某一块下面(每块瓷砖除图案外其它均相同),那么卡片藏在瓷砖下的概率为( )
A. B. C. D.
6. 一个小球在如图所示的方砖上自由滚动,并随机地停留在某块方砖上,则最终停在阴影部分上的概率是( )
A. B. C. D.不确定
7. “四时花竞巧,九子粽争新”,端午节吃粽子是我国的传统习俗.小南的妈妈在超市购买了豆沙粽和蛋黄粽共15个,这些粽子除了内部馅料不同外,其他均相同.小南从中任选了一个粽子,若她选到蛋黄粽的概率为,则购买的豆沙粽的个数是( )
A.5个 B.6个 C.8个 D.9个
8. 一儿童行走在如图所示每个格子都是正方形的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
9. 如图,一个游戏盘中,红、黄、蓝 三个扇形的圆心角度数分别为40°,120°,200°,让转盘自由转动,指针停止后在黄色区域的概率是( )
A. B. C. D.
10.抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
11.已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.0.5 D.0.25
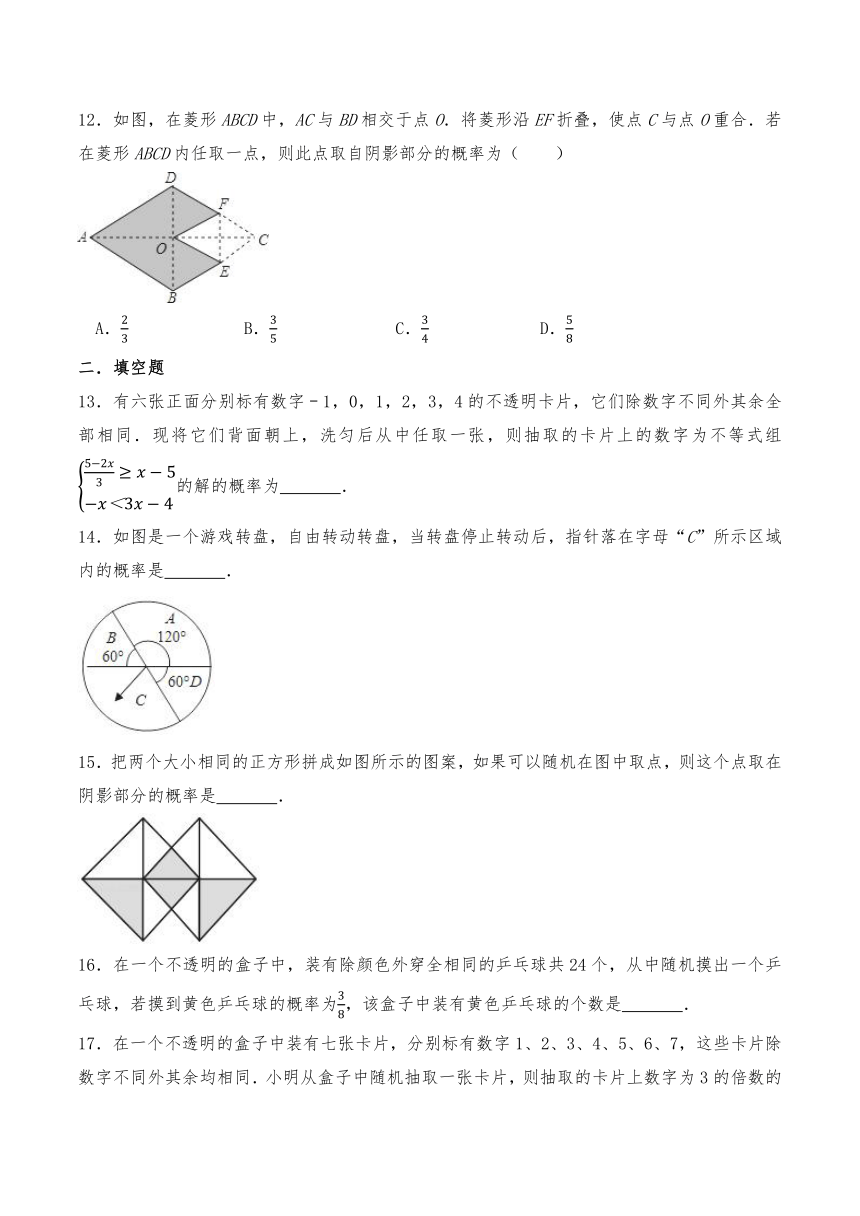
12.如图,在菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若在菱形ABCD内任取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
二.填空题
13.有六张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为 .
14.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在字母“C”所示区域内的概率是 .
15.把两个大小相同的正方形拼成如图所示的图案,如果可以随机在图中取点,则这个点取在阴影部分的概率是 .
16.在一个不透明的盒子中,装有除颜色外穿全相同的乒乓球共24个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为,该盒子中装有黄色乒乓球的个数是 .
17.在一个不透明的盒子中装有七张卡片,分别标有数字1、2、3、4、5、6、7,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片,则抽取的卡片上数字为3的倍数的概率是 .
18.如图,一飞镖游戏板由大小相同的小正方形格子组成,向游戏板内随机投掷一枚飞镖,击中黑色区域的概率是: .
19.掷一枚均匀的硬币,前20次抛掷的结果都是正面朝上,那么第21次抛掷的结果正面朝上的概率为 .
20.从﹣1,0,1,2,3这五个数中,随机取出一个数,记为a,那么使关于x的方程1有解,且使关于x的一元二次方程x2﹣3x+a=0有两个不相等的实数根的概率为 .
21.如图是一个正方形及其内切圆,正方形的边长为a.随机地往正方形内投一粒米,不落在圆内的概率是 .
22.如图,点O为正方形的中心,点E、F分别在正方形的边上,且∠EOF=90°,随机地往图中投一粒米,则米粒落在图中阴影部分的概率是 .
23.为了庆祝“六一儿童节”,育才初一年级同学在班会课进行了趣味活动,小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=4cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为 .
24.有六张正面分别标有数字﹣2,﹣1,0,2,3,4的不透明卡片,它们除数字不同外其余均相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为m,则使关于x的分式方程有正整数解的概率为 .
三.解答题
25.在一个不透明的袋子里装有2个白球,3个黄球,每个球除颜色外均相同,现将同样除颜色外都相同的黄球和白球若干个(白球个数是黄球个数的2倍)放入袋中,搅匀后,若从袋中摸出一个球是白球的概率是,求后放入袋中的黄球的个数.
26.某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买100元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在哪个区域,就根据所转结果付账.求一个顾客转动一次转盘但不打折的概率.
27.某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.
(1)他获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
(3)若要让获得20元购物券的概率变为,则转盘的颜色部分怎样修改?(直接写出修改方案即可).
28.疫情防控期间,随着人们健康意识的不断提升,洗手液需求量剧增.某商场计划引进多个品牌的洗手液进行销售.现邀请生产洗手液的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.两个厂家销售情况如下表:
甲厂家销量(件) 38 39 40 41 42
天数 2 4 2 1 1
乙厂家销量(件) 38 39 40 41 42
天数 1 2 2 4 1
(1)现从乙厂家试销的10天中随机抽取1天,求这1天的返利不超过160元的概率;
(2)商场拟甲、乙两个厂家中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
29.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况(1)从该企业的员工中随机抽取1人,求该员工手机月平均使用流量不超过900M的概率.
(2)据了解,某网络运营商推出两款流量套餮,详情如下
套餐名称 月套餐费(单位:元) 月套餐流量(单位:M)
A 20 700
B 30 1000
流量套餐的规则是:每月1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含200M的流量)需要10元,可以多次购买,如果当月流量有剩余,将会被清零.该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以人均所需费用为决策依据,该企业订购哪一款套餐更经济?
30.由于疫情对中小企业造成巨大的冲击,某市计划对该市的中小企业进行财政补贴.相关行业的主管部门为了解该市中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 ﹣0.60≤y<﹣0.40 ﹣0.40≤y<﹣0.20 ﹣0.20≤y<0 0≤y<0.20 0.20≤y<0.40
企业数 12 56 24 6 2
(同一组中的数据用该组数据的组中值为代表)
(1)分别估计该市的中小企业中产值增长率不低于20%的企业的概率以及产值增长率的平均数;
(2)该市有3000家中小企业,通过市场调研,去年该市的中小企业的第一季度平均产值是20万元,若要使一家中小企业保持良好的经营状态,必须保证其第一季度产值不能低于18万元.若要想让该市的所有中小企业保持良好的经营状态,该市应准备多少万元的补贴资金?
答案
一.选择题
C.A.D.D.C.A.B.B.B.B.A.C.
二.填空题
13..
14..
15..
16.9.
17..
18..
19.0.5.
20..
21.1.
22..
23..
24..
三.解答题
25.设放入袋中的黄球的个数为x个,根据题意得:
2+2x(2+3+x+2x)
解得:x=1,
答:放入袋中的黄球的个数有1个.
26.不打折的概率是:.
27.(1)∵共有20种等可能事件,其中满足条件的有11种,
∴P(中奖);
(2)由题意得:共有20种等可能结果,其中获100元购物券的有2种,获得50元购物券的有4种,获得20元购物券的有5种,
∴P(获得100元);
P(获得50元);
P(获得20元);
(3)直接将3个无色扇形涂为黄色.
28.(1)乙厂家,销售件数不超过40件,其获利就不超过160元,不超过40件的天数由5天,
∴;
(2),
甲每天获利70+39.5×2=149(元),
乙每天的获利162(元),
∵149<162,
∴选择乙厂家.
29.(1)由题意得,样本中月平均使用流量不超过900M的频数为:100﹣2﹣8=90,
则该员工手机月平均使用流量不超过900M的概率是;
(2)A套餐人均所需费用为:28(元),
B套餐人均所需费用为:30.2(元),
∵28<30.2,
∴该企业订购A套餐更经济.
30.(1),
(﹣0.5×12﹣0.3×56﹣0.1×24+0.1×6+0.3×2)=﹣24%,
答:估计该市的中小企业中产值增长率不低于20%的企业的概率为,产值增长率的平均数为﹣24%;
(2)对于﹣0.60≤y<﹣0.40,20(1﹣50%)=10,需补贴18﹣10=8(万);
对于﹣0.40≤y<﹣0.20,20(1﹣30%)=14,需补贴18﹣14=4(万);
对于﹣0.20≤y<0,20(1﹣10%)=18,需补贴18﹣18=0(万);
对于0≤y<0.20,需补贴0万;
对于0.20≤y<0.40,需补贴0万;
所以(12×8+56×4+0×24+0×6+0×2)×3000=9600(万).
答:该市应准备9600万元的补贴资金.
一.选择题
1. 一个不透明的盒子里装有红、黄、白三种颜色的球,个数分别为2、3、4,这些球除颜色外都相同,从盒子中任抽一个球,则抽到红球的概率是( )
A. B. C. D.
2. 在一个不透明的袋子里装有2个黑球3个白球,它们除颜色外都相同,随机从中摸出一个球,是黑球的概率是( )
A. B. C. D.
3. 从一副扑克牌中任意抽出1张牌,抽得下列牌中的概率最大的是( )
A.小王 B.大王 C.10 D.黑桃
4. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏:小明摸到的牌面是5(不放回),小颖从剩余的牌中抽取一张(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关),谁的牌面大谁就获胜.则小明获胜的概率是( )
A. B. C. D.
5. 如图,小亮有一个卡片藏在9块瓷砖中的某一块下面(每块瓷砖除图案外其它均相同),那么卡片藏在瓷砖下的概率为( )
A. B. C. D.
6. 一个小球在如图所示的方砖上自由滚动,并随机地停留在某块方砖上,则最终停在阴影部分上的概率是( )
A. B. C. D.不确定
7. “四时花竞巧,九子粽争新”,端午节吃粽子是我国的传统习俗.小南的妈妈在超市购买了豆沙粽和蛋黄粽共15个,这些粽子除了内部馅料不同外,其他均相同.小南从中任选了一个粽子,若她选到蛋黄粽的概率为,则购买的豆沙粽的个数是( )
A.5个 B.6个 C.8个 D.9个
8. 一儿童行走在如图所示每个格子都是正方形的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
9. 如图,一个游戏盘中,红、黄、蓝 三个扇形的圆心角度数分别为40°,120°,200°,让转盘自由转动,指针停止后在黄色区域的概率是( )
A. B. C. D.
10.抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
11.已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.0.5 D.0.25
12.如图,在菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若在菱形ABCD内任取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
二.填空题
13.有六张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为 .
14.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在字母“C”所示区域内的概率是 .
15.把两个大小相同的正方形拼成如图所示的图案,如果可以随机在图中取点,则这个点取在阴影部分的概率是 .
16.在一个不透明的盒子中,装有除颜色外穿全相同的乒乓球共24个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为,该盒子中装有黄色乒乓球的个数是 .
17.在一个不透明的盒子中装有七张卡片,分别标有数字1、2、3、4、5、6、7,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片,则抽取的卡片上数字为3的倍数的概率是 .
18.如图,一飞镖游戏板由大小相同的小正方形格子组成,向游戏板内随机投掷一枚飞镖,击中黑色区域的概率是: .
19.掷一枚均匀的硬币,前20次抛掷的结果都是正面朝上,那么第21次抛掷的结果正面朝上的概率为 .
20.从﹣1,0,1,2,3这五个数中,随机取出一个数,记为a,那么使关于x的方程1有解,且使关于x的一元二次方程x2﹣3x+a=0有两个不相等的实数根的概率为 .
21.如图是一个正方形及其内切圆,正方形的边长为a.随机地往正方形内投一粒米,不落在圆内的概率是 .
22.如图,点O为正方形的中心,点E、F分别在正方形的边上,且∠EOF=90°,随机地往图中投一粒米,则米粒落在图中阴影部分的概率是 .
23.为了庆祝“六一儿童节”,育才初一年级同学在班会课进行了趣味活动,小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=4cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为 .
24.有六张正面分别标有数字﹣2,﹣1,0,2,3,4的不透明卡片,它们除数字不同外其余均相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为m,则使关于x的分式方程有正整数解的概率为 .
三.解答题
25.在一个不透明的袋子里装有2个白球,3个黄球,每个球除颜色外均相同,现将同样除颜色外都相同的黄球和白球若干个(白球个数是黄球个数的2倍)放入袋中,搅匀后,若从袋中摸出一个球是白球的概率是,求后放入袋中的黄球的个数.
26.某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买100元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在哪个区域,就根据所转结果付账.求一个顾客转动一次转盘但不打折的概率.
27.某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.
(1)他获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
(3)若要让获得20元购物券的概率变为,则转盘的颜色部分怎样修改?(直接写出修改方案即可).
28.疫情防控期间,随着人们健康意识的不断提升,洗手液需求量剧增.某商场计划引进多个品牌的洗手液进行销售.现邀请生产洗手液的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.两个厂家销售情况如下表:
甲厂家销量(件) 38 39 40 41 42
天数 2 4 2 1 1
乙厂家销量(件) 38 39 40 41 42
天数 1 2 2 4 1
(1)现从乙厂家试销的10天中随机抽取1天,求这1天的返利不超过160元的概率;
(2)商场拟甲、乙两个厂家中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
29.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况(1)从该企业的员工中随机抽取1人,求该员工手机月平均使用流量不超过900M的概率.
(2)据了解,某网络运营商推出两款流量套餮,详情如下
套餐名称 月套餐费(单位:元) 月套餐流量(单位:M)
A 20 700
B 30 1000
流量套餐的规则是:每月1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含200M的流量)需要10元,可以多次购买,如果当月流量有剩余,将会被清零.该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以人均所需费用为决策依据,该企业订购哪一款套餐更经济?
30.由于疫情对中小企业造成巨大的冲击,某市计划对该市的中小企业进行财政补贴.相关行业的主管部门为了解该市中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 ﹣0.60≤y<﹣0.40 ﹣0.40≤y<﹣0.20 ﹣0.20≤y<0 0≤y<0.20 0.20≤y<0.40
企业数 12 56 24 6 2
(同一组中的数据用该组数据的组中值为代表)
(1)分别估计该市的中小企业中产值增长率不低于20%的企业的概率以及产值增长率的平均数;
(2)该市有3000家中小企业,通过市场调研,去年该市的中小企业的第一季度平均产值是20万元,若要使一家中小企业保持良好的经营状态,必须保证其第一季度产值不能低于18万元.若要想让该市的所有中小企业保持良好的经营状态,该市应准备多少万元的补贴资金?
答案
一.选择题
C.A.D.D.C.A.B.B.B.B.A.C.
二.填空题
13..
14..
15..
16.9.
17..
18..
19.0.5.
20..
21.1.
22..
23..
24..
三.解答题
25.设放入袋中的黄球的个数为x个,根据题意得:
2+2x(2+3+x+2x)
解得:x=1,
答:放入袋中的黄球的个数有1个.
26.不打折的概率是:.
27.(1)∵共有20种等可能事件,其中满足条件的有11种,
∴P(中奖);
(2)由题意得:共有20种等可能结果,其中获100元购物券的有2种,获得50元购物券的有4种,获得20元购物券的有5种,
∴P(获得100元);
P(获得50元);
P(获得20元);
(3)直接将3个无色扇形涂为黄色.
28.(1)乙厂家,销售件数不超过40件,其获利就不超过160元,不超过40件的天数由5天,
∴;
(2),
甲每天获利70+39.5×2=149(元),
乙每天的获利162(元),
∵149<162,
∴选择乙厂家.
29.(1)由题意得,样本中月平均使用流量不超过900M的频数为:100﹣2﹣8=90,
则该员工手机月平均使用流量不超过900M的概率是;
(2)A套餐人均所需费用为:28(元),
B套餐人均所需费用为:30.2(元),
∵28<30.2,
∴该企业订购A套餐更经济.
30.(1),
(﹣0.5×12﹣0.3×56﹣0.1×24+0.1×6+0.3×2)=﹣24%,
答:估计该市的中小企业中产值增长率不低于20%的企业的概率为,产值增长率的平均数为﹣24%;
(2)对于﹣0.60≤y<﹣0.40,20(1﹣50%)=10,需补贴18﹣10=8(万);
对于﹣0.40≤y<﹣0.20,20(1﹣30%)=14,需补贴18﹣14=4(万);
对于﹣0.20≤y<0,20(1﹣10%)=18,需补贴18﹣18=0(万);
对于0≤y<0.20,需补贴0万;
对于0.20≤y<0.40,需补贴0万;
所以(12×8+56×4+0×24+0×6+0×2)×3000=9600(万).
答:该市应准备9600万元的补贴资金.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
