九年级数学下册试题 第六章《图形的相似》单元复习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 第六章《图形的相似》单元复习-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 204.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 19:11:07 | ||
图片预览


文档简介
第六章《图形的相似》单元复习
一.选择题
1. 已知点E、F分别在△ABC的AB、AC边上,则下列判断正确的是( )
A.若△AEF与△ABC相似,则EF∥BC
B.若AE×BE=AF×FC,则△AEF与△ABC相似
C.若,则△AEF与△ABC相似
D.若AF BE=AE FC,则△AEF与△ABC相似
2. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF,BC=3,则DF=( )
A.4 B.3 C.2 D.
3. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC、BE、DO、DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )
A.①②③ B.①②④ C.①② D.②③④
4. 如图,AB∥CD∥EF,AD=4,BC=DF=3,则BE的长为( )
A. B. C.4 D.6
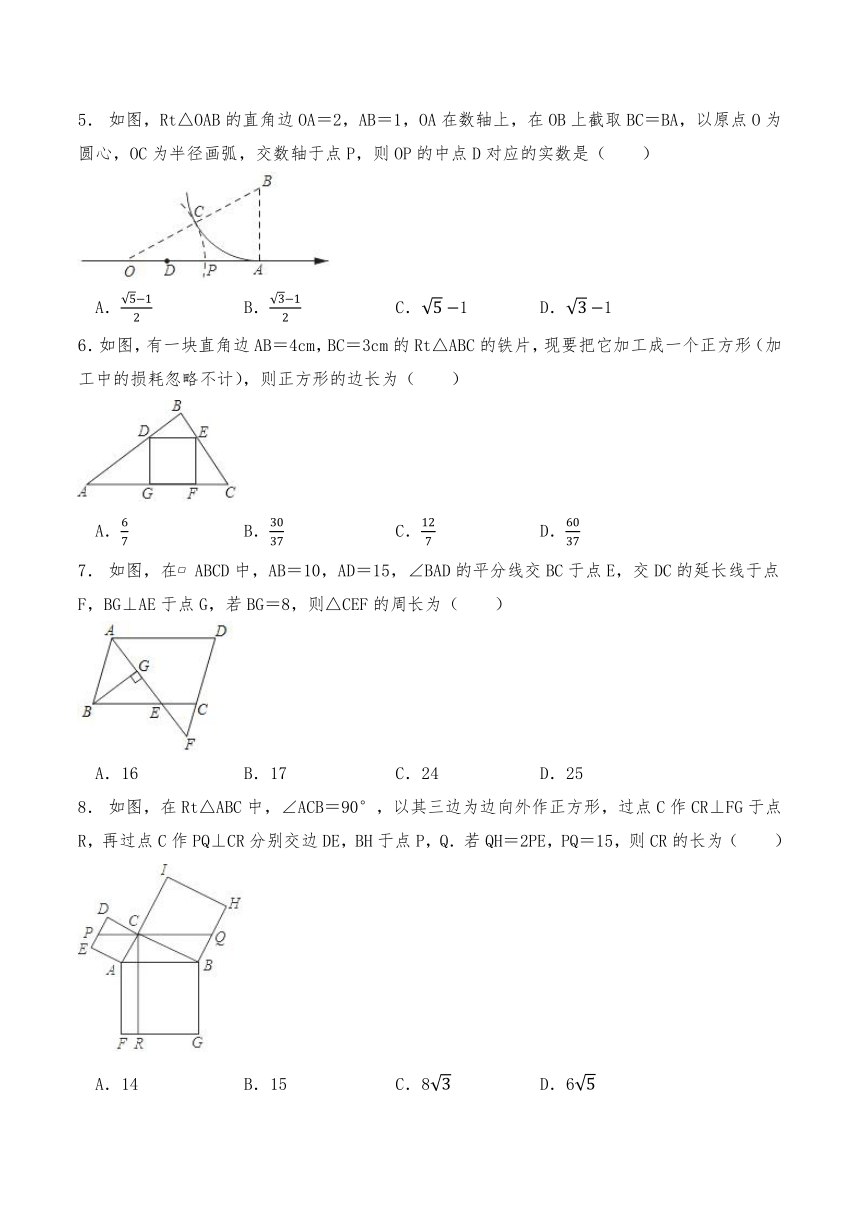
5. 如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A. B. C.1 D.1
6.如图,有一块直角边AB=4cm,BC=3cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
7. 如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
8. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为( )
A.14 B.15 C.8 D.6
9. 如图,△ABC中,AB=8,AC=6,∠A=90°,点D在△ABC内,且DB平分∠ABC,DC平分∠ACB,过点D作直线PQ,分别交AB、AC于点P、Q,若△APQ与△ABC相似,则线段PQ的长为( )
A.5 B. C.5或 D.6
10.如图,在 ABCD中,E、F分别是边BC、CD的中点,AE、AF分别交BD于点G、H,则图中阴影部分图形的面积与 ABCD的面积之比为( )
A.7:12 B.7:24 C.13:36 D.13:72
11.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的大小变化的情况是( )
A.一直减小 B.一直增大
C.先增大后减小 D.先减小后增大
二.填空题
12.如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=24,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为 .
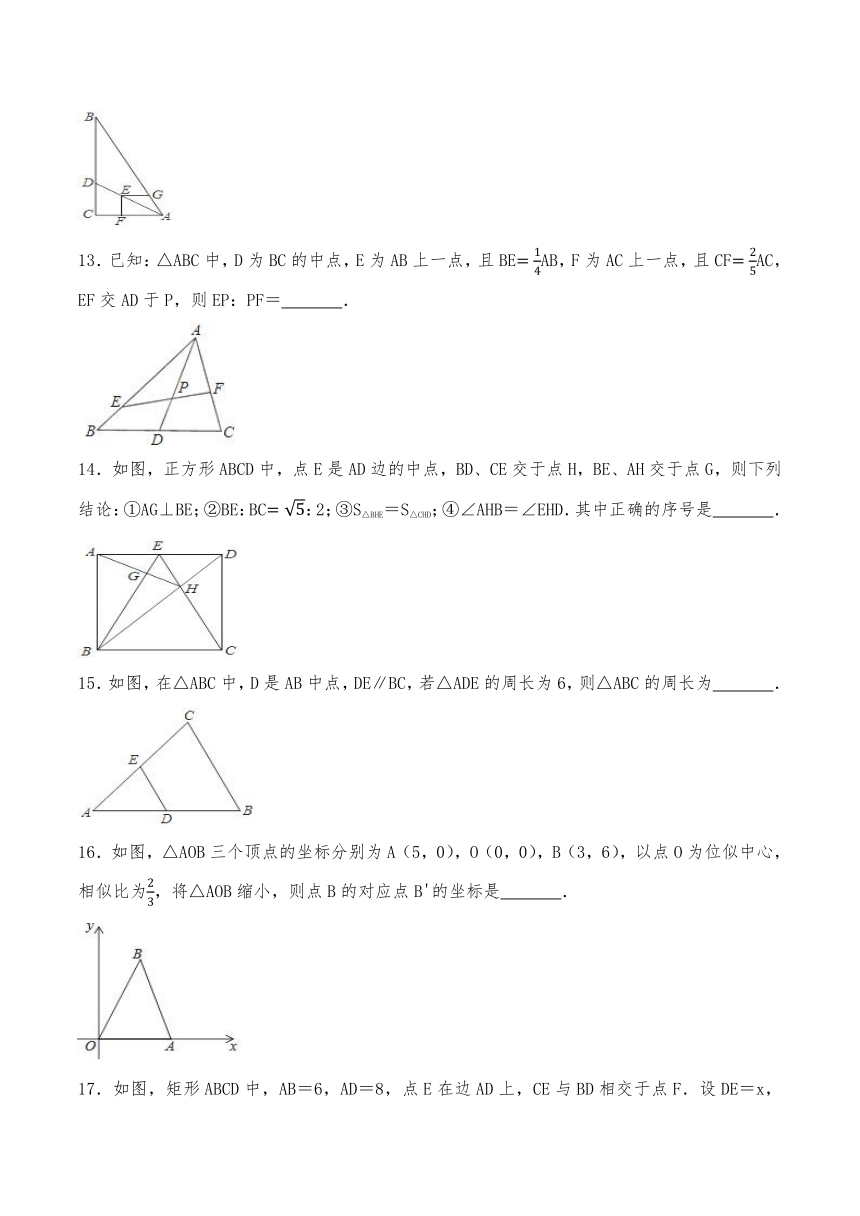
13.已知:△ABC中,D为BC的中点,E为AB上一点,且BEAB,F为AC上一点,且CFAC,EF交AD于P,则EP:PF= .
14.如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BE:BC:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的序号是 .
15.如图,在△ABC中,D是AB中点,DE∥BC,若△ADE的周长为6,则△ABC的周长为 .
16.如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B'的坐标是 .
17.如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,CE与BD相交于点F.设DE=x,BF=y,当0≤x≤8时,y关于x的函数解析式为 .
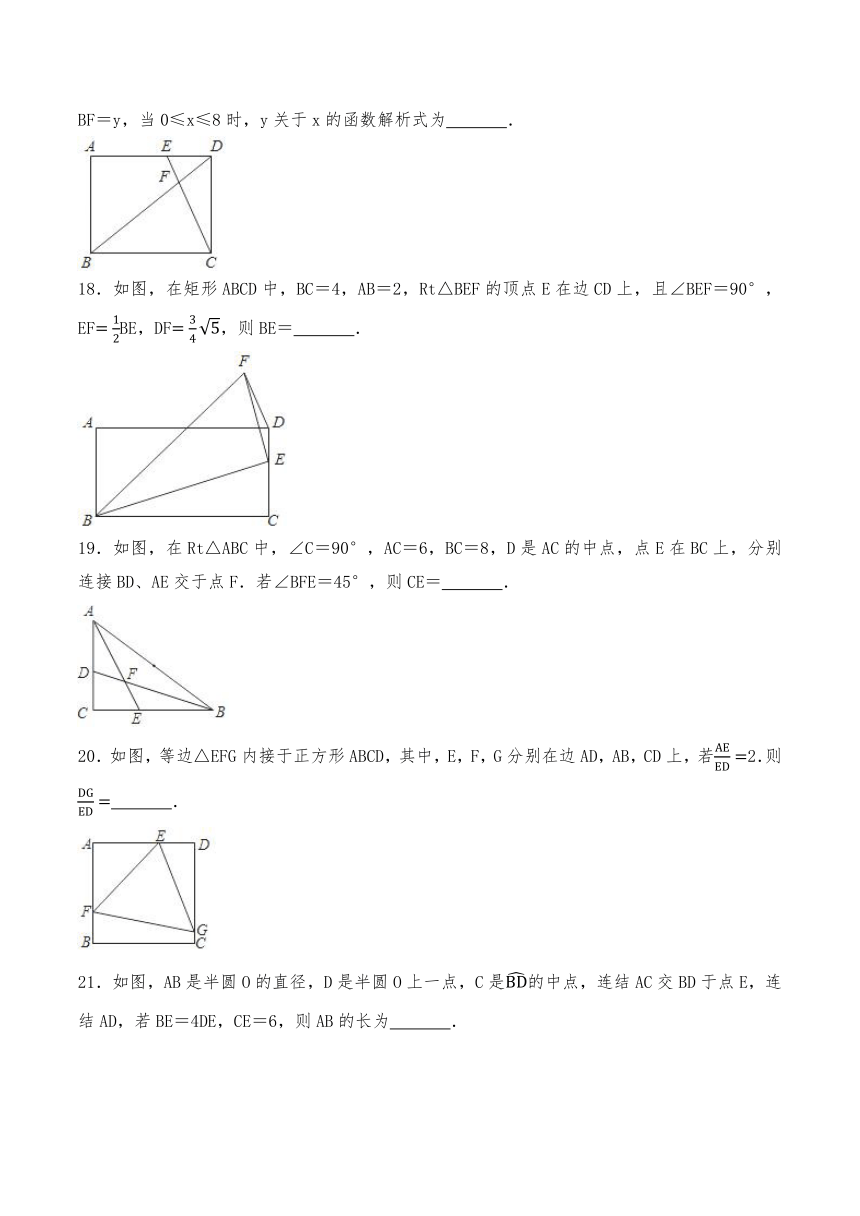
18.如图,在矩形ABCD中,BC=4,AB=2,Rt△BEF的顶点E在边CD上,且∠BEF=90°,EFBE,DF,则BE= .
19.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AC的中点,点E在BC上,分别连接BD、AE交于点F.若∠BFE=45°,则CE= .
20.如图,等边△EFG内接于正方形ABCD,其中,E,F,G分别在边AD,AB,CD上,若2.则 .
21.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连结AC交BD于点E,连结AD,若BE=4DE,CE=6,则AB的长为 .
22.如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,且AB=3,点E是边AB上的动点,当△ADE,△BCE,△CDE两两相似时,则AE= .
23.如图所示,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D、E分别在边AC、BC上,点F、G在AB边上.当四边形DEFG是菱形,且符合条件的菱形只有一个时,则菱形的边长l的取值范围是 .
三.解答题
24.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何?”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,求它的内接正方形CDEF的边长.
25.如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
(1)求BP的长;
(2)△EBM与△EPN相似吗?说明理由;
26.如图,在矩形ABCD中,点P是BC边上任意一点(点P不与B、C重合),连接AP,作PQ⊥AP,交CD于点Q,若AB=6,BC=8.
(1)试证明:△ABP∽△PCQ;
(2)当BP为多少时,CQ最长,最长是多少?
(3)试探究,是否存在一点P,使△APQ是等腰直角三角形?
27.如图,在矩形ABCD中,E是边AD上的一点,将△CDE沿CE折叠得到△CFE,点F恰好落在边AB上.
(1)证明:△AEF∽△BFC.
(2)若AB,BC=1,作线段CE的中垂线,交AB于点P,交CD于点Q,连结PE,PC.
①求线段DQ的长.
②试判断△PCE的形状,并说明理由.
28.如图,已知Rt△ABC,∠ACB=90°,AC=8,BC=6,D为射线AB上一动点,以CD为边画Rt△CDE,使∠DCE=90°,CE:CD=3:4,连接BE.
(1)求证:△CDA∽△CEB;
(2)在点D运动的过程中,求DE的最小值;
29.四边形ABCD中,∠ABC+∠ADC=180°,对角线BD平分∠ABC.
(1)如图1,延长BC,AD交于点M.
求证:①△MCD∽△MAB;
②AD=CD;
(2)如图2,连接AC交BD于点F,将△ABC沿着AC翻折得到△AEC,连接DE,若CE∥BD,BC=6,CD=4,求CF的长.
答案
一.选择题
D.B.B.A.A.D.A.A.B.B.D.
二.填空题
12.8.
13..
14.①②③④.
15.12.
16.(2,4)或(﹣2,﹣4).
17..
18..
19..
20..
21.4.
22.或1.
23.l或l
三.解答题
24.∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴,
∴,
∴x,
∴正方形CDEF的边长为.
25.(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠A=∠ABC=90°,
∵点E是边AD的中点,
∴AE=2,
∴BE2,
∵∠BEP=90°,
∴∠ABE+∠AEB=90°,∠EBP+∠ABE=90°,
∴∠AEB=∠PBE,
∵∠A=∠BEP=90°,
∴△ABE∽△EPB,
∴,即,
解得,PB=10;
(2)结论:△EBM∽△EPN,
理由:设BN交PE于O,
∵FH∥BP,
∴∠EHF=∠EPB=∠ENO,
∵∠EON=∠BOP,
∴△EON∽△BOP,
∴,
∴,又∵∠EOB=∠PON,
∴△EOB∽△NOP,
∴∠EBM=∠EPN,
∵∠BEP=∠MEN=90°,
∴∠BEM=∠PEN,
∴△EBM∽△EPN.
26.(1)∵PQ⊥AP,
∴∠APB+∠QPC=90°,
而∠QPC+∠PQC=90°,
∴∠APB=∠PQC,
∵∠ABP=∠PCQ=90°,
∴△ABP∽△PCQ;
(2)∵△ABP∽△PCQ,
∴,即,
则CQx2x(x﹣4)2,
故当x=4时,CQ的最大值为,
即BP为4时,CQ最长,最长是;
(3)∵△APQ是等腰直角三角形,则PA=PQ,
而△ABP∽△PCQ,
则△ABP≌△PCQ(AAS),
∴AB=PC=6,
则BP=8﹣6=2,
即BP=2时,△APQ是等腰直角三角形.
27.证明:(1)∵将△CDE沿CE折叠得到△CFE,
∴∠D=∠EFC=90°,
∴∠AFE+∠BFC=90°,
又∵∠AFE+∠AEF=90°,
∴∠AEF=∠BFC,
又∵∠A=∠B=90°,
∴△AEF∽△BFC;
(2)①连接EQ,
∵将△CDE沿CE折叠得到△CFE,
∴CD=CF,
∴BF1,
∴BC=BF=1,
∴∠BFC=∠BCF=45°,
∴∠AFE=45°=∠AEF,
∴AE=AF=AB﹣BF1,
∴DE=AD﹣AE=2,
∵PQ是EC的垂直平分线,
∴EQ=CQ,
∵EQ2=DQ2+DE2,
∴(DQ)2=DQ2+(2)2,
∴DQ=2;
②△PEC是等腰直角三角形,
理由如下:∵PQ是EC的垂直平分线,
∴PE=PC,
∵PE2=AE2+AP2,PC2=PB2+BC2,
∴(1)2+(BP)2=PB2+1,
∴BP1,
∴BP=AE,
在Rt△AEP和Rt△BPC中,
,
∴Rt△AEP≌Rt△BPC(HL),
∴∠APE=∠BCP,∠AEP=∠BPC,
∵∠APE+∠AEP=90°,
∴∠APE+∠BPC=90°,
∴∠EPC=90°,
∴△PEC是等腰直角三角形.
28.(1)证明:∵AC=8,BC=6,
∴BC:AC=3:4,
∵CE:CD=3:4,
∴,
∵∠ACB=∠DCE=90°,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
∴∠ACD=∠BCE,
∴△CDA∽△CEB;
(2)在Rt△ABC中,根据勾股定理得,AB=10,
在Rt△DCE中,CE:CD=3:4,
设CE=3x,CD=4x,则DE=5x,
要DE最小,则x最小,即CD最小,
而点D在射线AB上,
即当CD⊥AB时,CD最小,
∵AB CD最小AC BC,
∴CD最小,
∴DE的最小值为5x最小CD最小6;
29.(1)证明:①∵∠ABC+∠ADC=180°,∠MDC+∠ADC=180°,
∴∠MDC=∠ABC,
又∵∠M=∠M,
∴△MCD∽△MAB;
②连接AC,如图1所示:
∵①△MCD∽△MAB,
∴,
∴,
又∵∠M=∠M,
∴△MBD∽△MAC,
∴∠MBD=∠MAC,
∵∠ABC+∠ADC=180°,BD平分∠ABC,
∴2∠MBD+∠ADC=180°,
∵∠ADC+∠MAC+∠DCA=180°,
∴∠DCA=∠MBD,
∴∠DCA=∠MAC,
∴AD=CD;
(2)连接BE交AC于点N,如图2所示:
∵将△ABC沿着AC翻折得到△AEC,
∴点B与点E关于AC对称,EC=BC=6,
∴BN=EN,
∵CE∥BD,
∴∠CEN=∠FBN,
在△CEN和△FBN中,,
∴△CEN≌△FBN(ASA),
∴EC=BF=6,
∵∠ABC+∠ADC=180°,
∴A、B、C、D四点共圆,
∴∠DAC=∠DBC,
∵AD=CD,
∴∠DAC=∠DCA,
∴∠DBC=∠DCA,
又∵∠BDC=∠BDC,
∴△DBC∽△DCF,
∴,
∴DB DF=DC2,
∴DB (DB﹣BF)=DC2,
∴DB2﹣6DB=16,
解得:DB=8,或DB=﹣2(舍去),
∵,即,
解得:CF=3.
一.选择题
1. 已知点E、F分别在△ABC的AB、AC边上,则下列判断正确的是( )
A.若△AEF与△ABC相似,则EF∥BC
B.若AE×BE=AF×FC,则△AEF与△ABC相似
C.若,则△AEF与△ABC相似
D.若AF BE=AE FC,则△AEF与△ABC相似
2. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF,BC=3,则DF=( )
A.4 B.3 C.2 D.
3. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC、BE、DO、DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )
A.①②③ B.①②④ C.①② D.②③④
4. 如图,AB∥CD∥EF,AD=4,BC=DF=3,则BE的长为( )
A. B. C.4 D.6
5. 如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A. B. C.1 D.1
6.如图,有一块直角边AB=4cm,BC=3cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
7. 如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
8. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为( )
A.14 B.15 C.8 D.6
9. 如图,△ABC中,AB=8,AC=6,∠A=90°,点D在△ABC内,且DB平分∠ABC,DC平分∠ACB,过点D作直线PQ,分别交AB、AC于点P、Q,若△APQ与△ABC相似,则线段PQ的长为( )
A.5 B. C.5或 D.6
10.如图,在 ABCD中,E、F分别是边BC、CD的中点,AE、AF分别交BD于点G、H,则图中阴影部分图形的面积与 ABCD的面积之比为( )
A.7:12 B.7:24 C.13:36 D.13:72
11.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的大小变化的情况是( )
A.一直减小 B.一直增大
C.先增大后减小 D.先减小后增大
二.填空题
12.如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=24,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为 .
13.已知:△ABC中,D为BC的中点,E为AB上一点,且BEAB,F为AC上一点,且CFAC,EF交AD于P,则EP:PF= .
14.如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BE:BC:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的序号是 .
15.如图,在△ABC中,D是AB中点,DE∥BC,若△ADE的周长为6,则△ABC的周长为 .
16.如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B'的坐标是 .
17.如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,CE与BD相交于点F.设DE=x,BF=y,当0≤x≤8时,y关于x的函数解析式为 .
18.如图,在矩形ABCD中,BC=4,AB=2,Rt△BEF的顶点E在边CD上,且∠BEF=90°,EFBE,DF,则BE= .
19.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AC的中点,点E在BC上,分别连接BD、AE交于点F.若∠BFE=45°,则CE= .
20.如图,等边△EFG内接于正方形ABCD,其中,E,F,G分别在边AD,AB,CD上,若2.则 .
21.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连结AC交BD于点E,连结AD,若BE=4DE,CE=6,则AB的长为 .
22.如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,且AB=3,点E是边AB上的动点,当△ADE,△BCE,△CDE两两相似时,则AE= .
23.如图所示,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D、E分别在边AC、BC上,点F、G在AB边上.当四边形DEFG是菱形,且符合条件的菱形只有一个时,则菱形的边长l的取值范围是 .
三.解答题
24.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何?”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,求它的内接正方形CDEF的边长.
25.如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
(1)求BP的长;
(2)△EBM与△EPN相似吗?说明理由;
26.如图,在矩形ABCD中,点P是BC边上任意一点(点P不与B、C重合),连接AP,作PQ⊥AP,交CD于点Q,若AB=6,BC=8.
(1)试证明:△ABP∽△PCQ;
(2)当BP为多少时,CQ最长,最长是多少?
(3)试探究,是否存在一点P,使△APQ是等腰直角三角形?
27.如图,在矩形ABCD中,E是边AD上的一点,将△CDE沿CE折叠得到△CFE,点F恰好落在边AB上.
(1)证明:△AEF∽△BFC.
(2)若AB,BC=1,作线段CE的中垂线,交AB于点P,交CD于点Q,连结PE,PC.
①求线段DQ的长.
②试判断△PCE的形状,并说明理由.
28.如图,已知Rt△ABC,∠ACB=90°,AC=8,BC=6,D为射线AB上一动点,以CD为边画Rt△CDE,使∠DCE=90°,CE:CD=3:4,连接BE.
(1)求证:△CDA∽△CEB;
(2)在点D运动的过程中,求DE的最小值;
29.四边形ABCD中,∠ABC+∠ADC=180°,对角线BD平分∠ABC.
(1)如图1,延长BC,AD交于点M.
求证:①△MCD∽△MAB;
②AD=CD;
(2)如图2,连接AC交BD于点F,将△ABC沿着AC翻折得到△AEC,连接DE,若CE∥BD,BC=6,CD=4,求CF的长.
答案
一.选择题
D.B.B.A.A.D.A.A.B.B.D.
二.填空题
12.8.
13..
14.①②③④.
15.12.
16.(2,4)或(﹣2,﹣4).
17..
18..
19..
20..
21.4.
22.或1.
23.l或l
三.解答题
24.∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴,
∴,
∴x,
∴正方形CDEF的边长为.
25.(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠A=∠ABC=90°,
∵点E是边AD的中点,
∴AE=2,
∴BE2,
∵∠BEP=90°,
∴∠ABE+∠AEB=90°,∠EBP+∠ABE=90°,
∴∠AEB=∠PBE,
∵∠A=∠BEP=90°,
∴△ABE∽△EPB,
∴,即,
解得,PB=10;
(2)结论:△EBM∽△EPN,
理由:设BN交PE于O,
∵FH∥BP,
∴∠EHF=∠EPB=∠ENO,
∵∠EON=∠BOP,
∴△EON∽△BOP,
∴,
∴,又∵∠EOB=∠PON,
∴△EOB∽△NOP,
∴∠EBM=∠EPN,
∵∠BEP=∠MEN=90°,
∴∠BEM=∠PEN,
∴△EBM∽△EPN.
26.(1)∵PQ⊥AP,
∴∠APB+∠QPC=90°,
而∠QPC+∠PQC=90°,
∴∠APB=∠PQC,
∵∠ABP=∠PCQ=90°,
∴△ABP∽△PCQ;
(2)∵△ABP∽△PCQ,
∴,即,
则CQx2x(x﹣4)2,
故当x=4时,CQ的最大值为,
即BP为4时,CQ最长,最长是;
(3)∵△APQ是等腰直角三角形,则PA=PQ,
而△ABP∽△PCQ,
则△ABP≌△PCQ(AAS),
∴AB=PC=6,
则BP=8﹣6=2,
即BP=2时,△APQ是等腰直角三角形.
27.证明:(1)∵将△CDE沿CE折叠得到△CFE,
∴∠D=∠EFC=90°,
∴∠AFE+∠BFC=90°,
又∵∠AFE+∠AEF=90°,
∴∠AEF=∠BFC,
又∵∠A=∠B=90°,
∴△AEF∽△BFC;
(2)①连接EQ,
∵将△CDE沿CE折叠得到△CFE,
∴CD=CF,
∴BF1,
∴BC=BF=1,
∴∠BFC=∠BCF=45°,
∴∠AFE=45°=∠AEF,
∴AE=AF=AB﹣BF1,
∴DE=AD﹣AE=2,
∵PQ是EC的垂直平分线,
∴EQ=CQ,
∵EQ2=DQ2+DE2,
∴(DQ)2=DQ2+(2)2,
∴DQ=2;
②△PEC是等腰直角三角形,
理由如下:∵PQ是EC的垂直平分线,
∴PE=PC,
∵PE2=AE2+AP2,PC2=PB2+BC2,
∴(1)2+(BP)2=PB2+1,
∴BP1,
∴BP=AE,
在Rt△AEP和Rt△BPC中,
,
∴Rt△AEP≌Rt△BPC(HL),
∴∠APE=∠BCP,∠AEP=∠BPC,
∵∠APE+∠AEP=90°,
∴∠APE+∠BPC=90°,
∴∠EPC=90°,
∴△PEC是等腰直角三角形.
28.(1)证明:∵AC=8,BC=6,
∴BC:AC=3:4,
∵CE:CD=3:4,
∴,
∵∠ACB=∠DCE=90°,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
∴∠ACD=∠BCE,
∴△CDA∽△CEB;
(2)在Rt△ABC中,根据勾股定理得,AB=10,
在Rt△DCE中,CE:CD=3:4,
设CE=3x,CD=4x,则DE=5x,
要DE最小,则x最小,即CD最小,
而点D在射线AB上,
即当CD⊥AB时,CD最小,
∵AB CD最小AC BC,
∴CD最小,
∴DE的最小值为5x最小CD最小6;
29.(1)证明:①∵∠ABC+∠ADC=180°,∠MDC+∠ADC=180°,
∴∠MDC=∠ABC,
又∵∠M=∠M,
∴△MCD∽△MAB;
②连接AC,如图1所示:
∵①△MCD∽△MAB,
∴,
∴,
又∵∠M=∠M,
∴△MBD∽△MAC,
∴∠MBD=∠MAC,
∵∠ABC+∠ADC=180°,BD平分∠ABC,
∴2∠MBD+∠ADC=180°,
∵∠ADC+∠MAC+∠DCA=180°,
∴∠DCA=∠MBD,
∴∠DCA=∠MAC,
∴AD=CD;
(2)连接BE交AC于点N,如图2所示:
∵将△ABC沿着AC翻折得到△AEC,
∴点B与点E关于AC对称,EC=BC=6,
∴BN=EN,
∵CE∥BD,
∴∠CEN=∠FBN,
在△CEN和△FBN中,,
∴△CEN≌△FBN(ASA),
∴EC=BF=6,
∵∠ABC+∠ADC=180°,
∴A、B、C、D四点共圆,
∴∠DAC=∠DBC,
∵AD=CD,
∴∠DAC=∠DCA,
∴∠DBC=∠DCA,
又∵∠BDC=∠BDC,
∴△DBC∽△DCF,
∴,
∴DB DF=DC2,
∴DB (DB﹣BF)=DC2,
∴DB2﹣6DB=16,
解得:DB=8,或DB=﹣2(舍去),
∵,即,
解得:CF=3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
