九年级数学下册试题 第七章《锐角三角函数》综合练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 第七章《锐角三角函数》综合练习-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 19:12:52 | ||
图片预览




文档简介
第七章《锐角三角函数》综合练习
一.选择题
1. 在Rt△ABC中,∠C=90°,如果sinA,那么下列各式正确的是( )
A.AB=4AC B.AB=4BC C.AC=4BC D.BC=4AC
2. 在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA B.cotA C.sinA D.cosA
3. 如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB( )
A. B. C. D.
4. 在Rt△ABC中,∠A=90°,若∠B=30°,则sinC=( )
A. B. C. D.
5. 在Rt△ABC中,∠C=90°,AC,AB,则下列结论正确的是( )
A.sinB B.cosA C.tanB=2 D.tanA
6. 如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5 m B.10m C.5m D.8 m
7. 如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A. B. C.2 D.
8. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米
9. 某屋顶示意图如图所示,现要在屋顶上开一个天窗,天窗AB在水平位置,屋顶坡面长度PQ=QD=4.8米,则屋顶水平跨度PD的长为( )米
A.cosα B.cosα C.sinα D.sinα
10.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )
A. B. C. D.
11.在Rt△ABC中,∠C=90°,BC=3,AC=2,则sinA的值为( )
A. B. C. D.
12.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
A.15米 B.16米 C.17米 D.18米
二.填空题
13.已知α是锐角,且sin(α+15°),那么tanα= .
14.计算:cos60°tan30°+cot60°= .
15.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA= .
16.如图,在市区A道路上建造一座立交桥,要求桥面的高度h为4.8米,引桥的坡角为14°,则引桥的水平距离l为 米(结果精确到0.1m,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25).
17.已知tan(α+15°),则tanα的值为 .
18.小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度 .(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
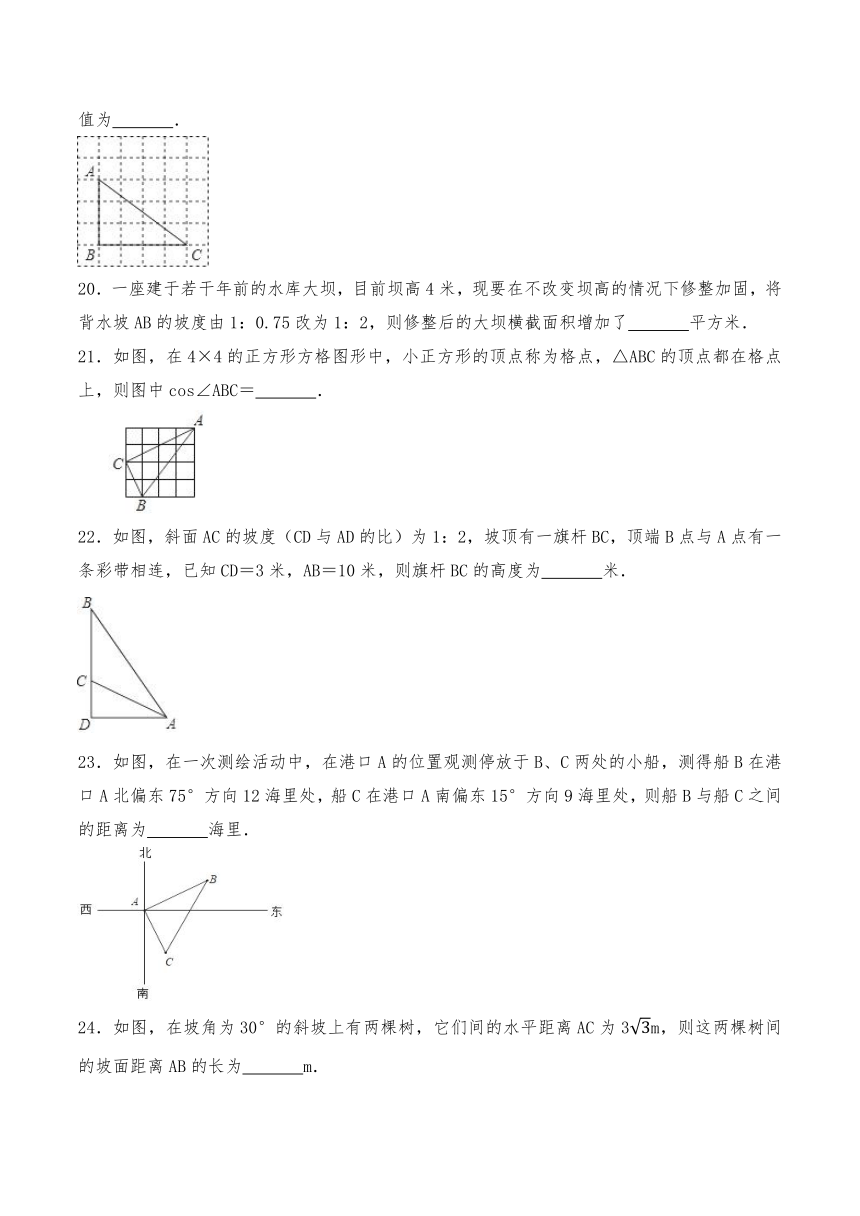
19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA的值为 .
20.一座建于若干年前的水库大坝,目前坝高4米,现要在不改变坝高的情况下修整加固,将背水坡AB的坡度由1:0.75改为1:2,则修整后的大坝横截面积增加了 平方米.
21.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC= .
22.如图,斜面AC的坡度(CD与AD的比)为1:2,坡顶有一旗杆BC,顶端B点与A点有一条彩带相连,已知CD=3米,AB=10米,则旗杆BC的高度为 米.
23.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
24.如图,在坡角为30°的斜坡上有两棵树,它们间的水平距离AC为3m,则这两棵树间的坡面距离AB的长为 m.
三.解答题
25.如图,某野外生态考察小组早晨7点整从A营地出发,准备前往正东方向的B营地,由于一条南北向河流的阻挡(图中阴影部分),他们需要从C处过桥,经过测量得知,A、B之间的距离为13km,∠A和∠B的度数分别是37°和53°,桥CD的长度是0.5km,图中的区域CDFE近似看做一个矩形区域.
(1)求CE的长;
(2)该考察小组希望到达B营地的时间不迟于中午12点,则他们的行进速度至少是多少?(结果保留1位小数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
26.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
27.清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”.是修武作为“千年古县”的标志性古建筑,为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在A处,眼睛E距离地面的高度为1.85m,测得塔顶C的仰角为45°,小红站在距离小明10m的D处,眼睛F距离地面的高度为1.5m,测得塔顶C的仰角为60°,已知A,D,塔底B在同一水平面上,由此即可求出塔高BC.你知道是怎么求的吗?请写出解题过程.(结果精确到1m.参考数据:1.732)
28.如图,在△ABC中,∠B=45°,AC=5,cosC,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
29.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
30.第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会,其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°,此时,两人的水平距离EC为4m,已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.
(参考数据:sin53°,cos53°,tan53°)
答案
一.选择题
B.A.C.D.B.B.A.A.B.B.D.B.
二.填空题
13.1.
14..
15..
16.19.2.
17.1.
18.233米.
19..
20.10.
21..
22.5.
23.15.
24.6.
三.解答题
25.(1)设CE=DF=x,
由题意可知:CD=EF=0.5,
在Rt△ACE中,
∴tan37°,
∴AE
在Rt△DBF中,
tan37°,
∴BF=DF tan37°,
∴0.5+0.75x=13,
解得:x=6,
即CE=6.
(2)由题意可知:行进时间最多5小时,
∵sin37°,cos37°,
∴AC10,BD7.5
AC+CD+BD=10+0.5+7.5=18
∴行进速度至少为18÷5=3.6km/h,
答:他们的行进速度至少是3.6km/h
26.在Rt△CDB中,tan∠BDC,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
27.过E点作EG⊥BC于G,过F点作FH⊥BC于H,
设BC=xm,则CG=(x﹣1.85)m,CH=(x﹣1.5)m,
在Rt△CHF中,FH,
Rt△CGE中,EG(x﹣1.85)m,
∵EG﹣FH=10,
∴(x﹣1.85)10,
解得x≈26.
故塔高BC大约26m高.
28.(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,AC=5,cosC,
∴CD=AC cosC=3,
∴AD4.
(2)∵∠B=45°,∠ADB=90°,
∴∠BAD=90°﹣∠B=45°,
∴∠B=∠BAD,
∴BD=AD=4,
∴S△ABCAD BC4×(4+3)=14.
29.(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DCBC=9,
∴AB3,
∴sinB;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴,
∴EFAD6=4,BFBD9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE5.
30.作DF⊥AB于F,
设AB=xm,
∵FB⊥EB,DE⊥EB,DF⊥AB,
∴四边形FBED为矩形,
∴FB=DE=10,DF=BE,
∴AF=10﹣x,
在Rt△AFD中,∠ADF=45°,
∴DF=AF=x﹣10,
在Rt△ABC中,∠ACB=53°,tan∠ACB,
∴BCx,
由题意得,BE﹣BC=CE,即x﹣10x=4,
解得,x=56,
答:钟楼AB的高度约为56m.
一.选择题
1. 在Rt△ABC中,∠C=90°,如果sinA,那么下列各式正确的是( )
A.AB=4AC B.AB=4BC C.AC=4BC D.BC=4AC
2. 在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA B.cotA C.sinA D.cosA
3. 如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB( )
A. B. C. D.
4. 在Rt△ABC中,∠A=90°,若∠B=30°,则sinC=( )
A. B. C. D.
5. 在Rt△ABC中,∠C=90°,AC,AB,则下列结论正确的是( )
A.sinB B.cosA C.tanB=2 D.tanA
6. 如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5 m B.10m C.5m D.8 m
7. 如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A. B. C.2 D.
8. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米
9. 某屋顶示意图如图所示,现要在屋顶上开一个天窗,天窗AB在水平位置,屋顶坡面长度PQ=QD=4.8米,则屋顶水平跨度PD的长为( )米
A.cosα B.cosα C.sinα D.sinα
10.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )
A. B. C. D.
11.在Rt△ABC中,∠C=90°,BC=3,AC=2,则sinA的值为( )
A. B. C. D.
12.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
A.15米 B.16米 C.17米 D.18米
二.填空题
13.已知α是锐角,且sin(α+15°),那么tanα= .
14.计算:cos60°tan30°+cot60°= .
15.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA= .
16.如图,在市区A道路上建造一座立交桥,要求桥面的高度h为4.8米,引桥的坡角为14°,则引桥的水平距离l为 米(结果精确到0.1m,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25).
17.已知tan(α+15°),则tanα的值为 .
18.小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度 .(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA的值为 .
20.一座建于若干年前的水库大坝,目前坝高4米,现要在不改变坝高的情况下修整加固,将背水坡AB的坡度由1:0.75改为1:2,则修整后的大坝横截面积增加了 平方米.
21.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC= .
22.如图,斜面AC的坡度(CD与AD的比)为1:2,坡顶有一旗杆BC,顶端B点与A点有一条彩带相连,已知CD=3米,AB=10米,则旗杆BC的高度为 米.
23.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
24.如图,在坡角为30°的斜坡上有两棵树,它们间的水平距离AC为3m,则这两棵树间的坡面距离AB的长为 m.
三.解答题
25.如图,某野外生态考察小组早晨7点整从A营地出发,准备前往正东方向的B营地,由于一条南北向河流的阻挡(图中阴影部分),他们需要从C处过桥,经过测量得知,A、B之间的距离为13km,∠A和∠B的度数分别是37°和53°,桥CD的长度是0.5km,图中的区域CDFE近似看做一个矩形区域.
(1)求CE的长;
(2)该考察小组希望到达B营地的时间不迟于中午12点,则他们的行进速度至少是多少?(结果保留1位小数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
26.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
27.清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”.是修武作为“千年古县”的标志性古建筑,为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在A处,眼睛E距离地面的高度为1.85m,测得塔顶C的仰角为45°,小红站在距离小明10m的D处,眼睛F距离地面的高度为1.5m,测得塔顶C的仰角为60°,已知A,D,塔底B在同一水平面上,由此即可求出塔高BC.你知道是怎么求的吗?请写出解题过程.(结果精确到1m.参考数据:1.732)
28.如图,在△ABC中,∠B=45°,AC=5,cosC,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
29.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
30.第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会,其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°,此时,两人的水平距离EC为4m,已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.
(参考数据:sin53°,cos53°,tan53°)
答案
一.选择题
B.A.C.D.B.B.A.A.B.B.D.B.
二.填空题
13.1.
14..
15..
16.19.2.
17.1.
18.233米.
19..
20.10.
21..
22.5.
23.15.
24.6.
三.解答题
25.(1)设CE=DF=x,
由题意可知:CD=EF=0.5,
在Rt△ACE中,
∴tan37°,
∴AE
在Rt△DBF中,
tan37°,
∴BF=DF tan37°,
∴0.5+0.75x=13,
解得:x=6,
即CE=6.
(2)由题意可知:行进时间最多5小时,
∵sin37°,cos37°,
∴AC10,BD7.5
AC+CD+BD=10+0.5+7.5=18
∴行进速度至少为18÷5=3.6km/h,
答:他们的行进速度至少是3.6km/h
26.在Rt△CDB中,tan∠BDC,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
27.过E点作EG⊥BC于G,过F点作FH⊥BC于H,
设BC=xm,则CG=(x﹣1.85)m,CH=(x﹣1.5)m,
在Rt△CHF中,FH,
Rt△CGE中,EG(x﹣1.85)m,
∵EG﹣FH=10,
∴(x﹣1.85)10,
解得x≈26.
故塔高BC大约26m高.
28.(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,AC=5,cosC,
∴CD=AC cosC=3,
∴AD4.
(2)∵∠B=45°,∠ADB=90°,
∴∠BAD=90°﹣∠B=45°,
∴∠B=∠BAD,
∴BD=AD=4,
∴S△ABCAD BC4×(4+3)=14.
29.(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DCBC=9,
∴AB3,
∴sinB;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴,
∴EFAD6=4,BFBD9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE5.
30.作DF⊥AB于F,
设AB=xm,
∵FB⊥EB,DE⊥EB,DF⊥AB,
∴四边形FBED为矩形,
∴FB=DE=10,DF=BE,
∴AF=10﹣x,
在Rt△AFD中,∠ADF=45°,
∴DF=AF=x﹣10,
在Rt△ABC中,∠ACB=53°,tan∠ACB,
∴BCx,
由题意得,BE﹣BC=CE,即x﹣10x=4,
解得,x=56,
答:钟楼AB的高度约为56m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
