湖北省宜昌市长阳土家族自治县重点中学2023-2024学年高一上学期12月月考数学试题(含解析)
文档属性
| 名称 | 湖北省宜昌市长阳土家族自治县重点中学2023-2024学年高一上学期12月月考数学试题(含解析) | 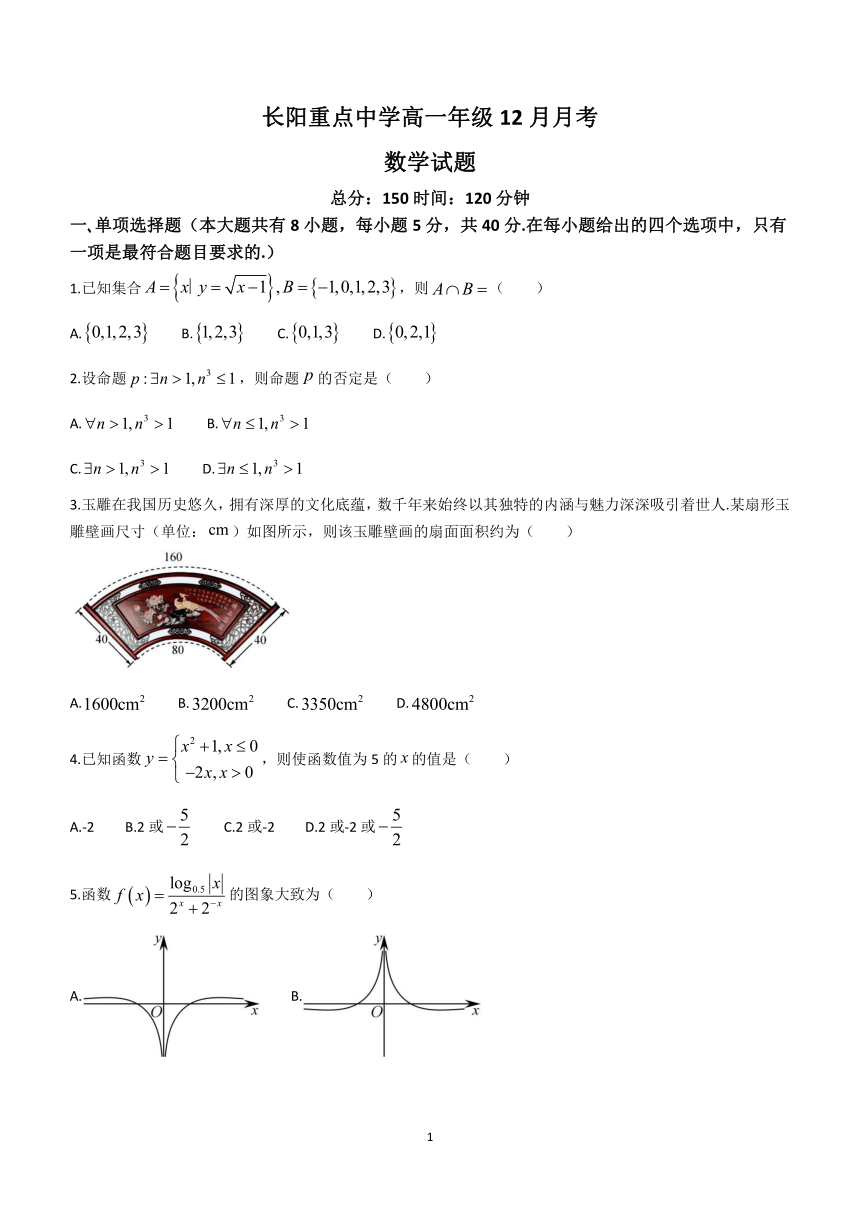 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 13:38:09 | ||
图片预览





文档简介
长阳重点中学高一年级12月月考
数学试题
总分:150时间:120分钟
一 单项选择题(本大题共有8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是最符合题目要求的.)
1.已知集合,则( )
A. B. C. D.
2.设命题,则命题的否定是( )
A. B.
C. D.
3.玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.某扇形玉雕壁画尺寸(单位:)如图所示,则该玉雕壁画的扇面面积约为( )
A. B. C. D.
4.已知函数,则使函数值为5的的值是( )
A.-2 B.2或 C.2或-2 D.2或-2或
5.函数的图象大致为( )
A. B.
C. D.
6.某网红城市鹅城人口模型近似为(单位:万人),其中表示2015年的人口数量,则鹅城人口数量达到60万的年份大约是( )(参考数据:)
A.2037年 B.2047年 C.2057年 D.2067年
7.函数在区间上的值域为( )
A. B. C. D.
8.若定义在上的函数同时满足:①为奇函数;②对任意的,且都有,则称函数具有性质.已知函数具有性质,则不等式的解集为( )
A. B.
C. D.
二 多选题(本大题共有4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合要求,全部选对得5分,部分选对得2分,有选错的得0分.)
9.若函数的图象是连续的,且函数的唯一零点同在区间内,则与符号不同的是( )
A. B. C. D.
10.下列判断正确的是( )
A. B.若,则
C. D.
11.下列说法错误的是( )
A.函数的值域为,则,或
B.若,则函数的最小值为2
C.是的充分不必要条件
D.当时,不等式恒成立,则的取值范围是
12.己知函数是定义在上的奇函数,当时,,若关于的方程恰有4个不相等的实数根,则实数的值可能为( )
A. B.0 C. D.
三 填空题(本大题共有4小题,每小题5分,共20分.)
13.已知,则的最小值为__________.
14.函数的定义域为__________.
15.若是关于的方程的两个根,则__________.
16.定义域为的函数满足,且当时,0恒成立,设,则的大小关系为__________.(从大到小排列)
四 解答题(本大题共有6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.)
17.(10分)(1)计算:;
(2)已知关于的不等式的解集为,求不等式的解集.
18.(12分)已知,
(1)求的值;
(2)求;
19.(12分)已知集合,集合.
(1)若,求实数的取值范围;
(2)命题,命题,若是的充分条件,求实数的取值集合.
20.(12分)杭州亚运会田径比赛10月5日迎来收官,在最后两个竞技项目男女马拉松比赛中,中国选手何杰以2小时13分02秒夺得男子组冠军,这是中国队亚运史上首枚男子马拉松金牌.人类长跑运动一般分为两个阶段,第一阶段为前1小时的稳定阶段,第二阶段为疲劳阶段.现一的复健马拉松运动员进行4小时长跑训练,假设其稳定阶段作速度为的匀速运动,该阶段每千克体重消耗体力表示该阶段所用时间),疲劳阶段由于体力消耗过大变为的减速运动(表示该阶段所用时间).疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力.已知该运动员初始体力为.不考虑其他因素,所用时间为(单位:),请回答下列问题:
(1)请写出该运动员剩余体力关于时间的函数;
(2)该运动员在4小时内何时体力达到最低值,最低值为多少?
21.(12分)已知是定义在上的奇函数,满足,且当时,有.
(1)解不等式:;
(2)若对所有恒成立,求实数的取值范围.
22.(12分)已知函数的单调递减区间为,函数.
(1)求实数的值,并写出函数的单调递增区间(不用写出求解过程);
(2)证明:方程在内有且仅有一个根;
(3)在条件(2)下,证明:.(参考数据)
2023-2024学年高一第一学期12月月考
数学试卷答案
一 单项选择题
1.【答案】B
【详解】集合.
2.【答案】A
【详解】命题的否定是
3.【答案】D
【详解】易知该扇形玉雕壁画可看作由一个大扇形剪去一个小扇形得到,设大 小扇形所在圆的半径分别为,相同的圆心角为,则,得,又因为,所以,该扇形玉雕壁画面积
4.【答案】A
【详解】当时,
.
当时,,不合题意.
故.
5.【答案】B
【详解】函数的定义域为,
所以为偶函数,排除选项,
当时,,
则,排除选项.
故选:B.
6.【答案】C
【详解】,即,
,
7.【答案】D
【详解】函数,易得函数在上单调递减,在上单调递减,当时,;当时,.所以,函数的值域为.
8.【答案】B
【详解】对任意的,且,都有,
即对任意两个不相等的正实数,不妨设,
都有,所以有,
所以函数是上的减函数,
又因为为奇函数,即有,有
所以有,所以为偶函数,
所以在上单调递增.
①当,即时,有,由,
得,所以,解得,此时无解;
②当,即时,由,得,
所以,解得或.
综上所述:不等式的解集为.
故选:B
二 多选题
9.【答案】ABD
【详解】由二分法的步骤可知,
①零点在内,则有,不妨设,取中点2;
②零点在内,则有,则,取中点1;
③零点在内,则有,则,取中点;
④零点在内,则有,则,则取中点;
⑤零点在内,则有,则,
所以与符号不同的是,
10.【答案】AB
【详解】对选项A:,正确;
对选项B:,故,正确;
对选项C:要证,即,即,不成立;
对选项D:,错误;
11.【答案】BD
【详解】对选项A:函数的值域为,则,
解得或,正确;
对选项B:,
当且仅当,即时等号成立,等号成立条件不满足,错误;
对选项C:,即,
函数单调递增,故,即;
取满足,不成立,正确;
对选项D:当时,不等式恒成立,错误;
12.【答案】AC
【详解】由于函数是定义在上的奇函数,所以讨论情况如下:
作图像如下图所示,
关于的方程,
解得或
由于与图像有一个公共点,
则图像与图像有三个公共点,如图所示,,
同理,时,,所以实数的值是.
三 填空题
13.【答案】
【详解】由题得,,且,
所以,
,当且仅当时等号成立.
14.【答案】
【详解】函数的定义域满足:,
解得且.
故答案为:.
15.【答案】
【详解】由题意得,
则或,
又,即,解得或(舍去),
则,
所以
.
故答案为:.
16.【答案】
【解析】因为函数满足,所以函数的图象关于直线成轴对称,
因为当时,,由,则,即,
所以在上单调递增,则在上单调递减,
由,
由,根据函数在上单调递增,则;
由,根据函数在上单调递增,则.
由函数在上单调递减,则,即.
四 解答题
17.【答案】(1);(2)
【详解】(1)
.
(2)由不等式的解集为,得,解答
则,即,解得,即原不等式的解集为.
18.【答案】(1)2;(2).
【详解】(1)由已知,
化简得,整理得故
(2)
.
19.【答案】(1);(2
【详解】(1)由,即,
所以,解得,所以,
因为,
当时,,解得,
当时,或,
解得或,
综上可得实数的取值范围为.
(2)是的充分条件,,
,解得或,
即实数的取值集合为.
20.【答案】(1)
(2)时有最小值,最小值为.
【详解】(1)由题可先写出速度关于时间的函数,
代入与公式可得
解得;
(2)①稳定阶段中单调递减,此过程中最小值;
②疲劳阶段,
则有,
当且仅当,即时,“成立,
所以疲劳阶段中体力最低值为,
由于,因此,在时,运动员体力有最小值.
21.【答案】(1);(2)
解:(1)为奇函数,所以,
则由,得,得,
故函数在上单调递增.
则
解得,故不等式的解集为.
(2)因为,所以.
若对所有恒成立,
则成立,且,
所以对恒成立,即对恒成立.
令,
则即得
解得
故实数的取值范围是.
22.【答案】(1)
(2)证明见解析(3)证明见解析
【解析】
(1)函数的单调递减区间为,故,,
函数定义域满足:,解得或,
在上单调递增,在上单调递增,
故函数的单调递增区间为;
(2),即,即,
设,函数在上单调递增,
,故在上有唯一零点,
即方程在内有且仅有一个根;
(3),要证,即,函数在上单调递增,
故,即,得证.
数学试题
总分:150时间:120分钟
一 单项选择题(本大题共有8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是最符合题目要求的.)
1.已知集合,则( )
A. B. C. D.
2.设命题,则命题的否定是( )
A. B.
C. D.
3.玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.某扇形玉雕壁画尺寸(单位:)如图所示,则该玉雕壁画的扇面面积约为( )
A. B. C. D.
4.已知函数,则使函数值为5的的值是( )
A.-2 B.2或 C.2或-2 D.2或-2或
5.函数的图象大致为( )
A. B.
C. D.
6.某网红城市鹅城人口模型近似为(单位:万人),其中表示2015年的人口数量,则鹅城人口数量达到60万的年份大约是( )(参考数据:)
A.2037年 B.2047年 C.2057年 D.2067年
7.函数在区间上的值域为( )
A. B. C. D.
8.若定义在上的函数同时满足:①为奇函数;②对任意的,且都有,则称函数具有性质.已知函数具有性质,则不等式的解集为( )
A. B.
C. D.
二 多选题(本大题共有4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合要求,全部选对得5分,部分选对得2分,有选错的得0分.)
9.若函数的图象是连续的,且函数的唯一零点同在区间内,则与符号不同的是( )
A. B. C. D.
10.下列判断正确的是( )
A. B.若,则
C. D.
11.下列说法错误的是( )
A.函数的值域为,则,或
B.若,则函数的最小值为2
C.是的充分不必要条件
D.当时,不等式恒成立,则的取值范围是
12.己知函数是定义在上的奇函数,当时,,若关于的方程恰有4个不相等的实数根,则实数的值可能为( )
A. B.0 C. D.
三 填空题(本大题共有4小题,每小题5分,共20分.)
13.已知,则的最小值为__________.
14.函数的定义域为__________.
15.若是关于的方程的两个根,则__________.
16.定义域为的函数满足,且当时,0恒成立,设,则的大小关系为__________.(从大到小排列)
四 解答题(本大题共有6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.)
17.(10分)(1)计算:;
(2)已知关于的不等式的解集为,求不等式的解集.
18.(12分)已知,
(1)求的值;
(2)求;
19.(12分)已知集合,集合.
(1)若,求实数的取值范围;
(2)命题,命题,若是的充分条件,求实数的取值集合.
20.(12分)杭州亚运会田径比赛10月5日迎来收官,在最后两个竞技项目男女马拉松比赛中,中国选手何杰以2小时13分02秒夺得男子组冠军,这是中国队亚运史上首枚男子马拉松金牌.人类长跑运动一般分为两个阶段,第一阶段为前1小时的稳定阶段,第二阶段为疲劳阶段.现一的复健马拉松运动员进行4小时长跑训练,假设其稳定阶段作速度为的匀速运动,该阶段每千克体重消耗体力表示该阶段所用时间),疲劳阶段由于体力消耗过大变为的减速运动(表示该阶段所用时间).疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力.已知该运动员初始体力为.不考虑其他因素,所用时间为(单位:),请回答下列问题:
(1)请写出该运动员剩余体力关于时间的函数;
(2)该运动员在4小时内何时体力达到最低值,最低值为多少?
21.(12分)已知是定义在上的奇函数,满足,且当时,有.
(1)解不等式:;
(2)若对所有恒成立,求实数的取值范围.
22.(12分)已知函数的单调递减区间为,函数.
(1)求实数的值,并写出函数的单调递增区间(不用写出求解过程);
(2)证明:方程在内有且仅有一个根;
(3)在条件(2)下,证明:.(参考数据)
2023-2024学年高一第一学期12月月考
数学试卷答案
一 单项选择题
1.【答案】B
【详解】集合.
2.【答案】A
【详解】命题的否定是
3.【答案】D
【详解】易知该扇形玉雕壁画可看作由一个大扇形剪去一个小扇形得到,设大 小扇形所在圆的半径分别为,相同的圆心角为,则,得,又因为,所以,该扇形玉雕壁画面积
4.【答案】A
【详解】当时,
.
当时,,不合题意.
故.
5.【答案】B
【详解】函数的定义域为,
所以为偶函数,排除选项,
当时,,
则,排除选项.
故选:B.
6.【答案】C
【详解】,即,
,
7.【答案】D
【详解】函数,易得函数在上单调递减,在上单调递减,当时,;当时,.所以,函数的值域为.
8.【答案】B
【详解】对任意的,且,都有,
即对任意两个不相等的正实数,不妨设,
都有,所以有,
所以函数是上的减函数,
又因为为奇函数,即有,有
所以有,所以为偶函数,
所以在上单调递增.
①当,即时,有,由,
得,所以,解得,此时无解;
②当,即时,由,得,
所以,解得或.
综上所述:不等式的解集为.
故选:B
二 多选题
9.【答案】ABD
【详解】由二分法的步骤可知,
①零点在内,则有,不妨设,取中点2;
②零点在内,则有,则,取中点1;
③零点在内,则有,则,取中点;
④零点在内,则有,则,则取中点;
⑤零点在内,则有,则,
所以与符号不同的是,
10.【答案】AB
【详解】对选项A:,正确;
对选项B:,故,正确;
对选项C:要证,即,即,不成立;
对选项D:,错误;
11.【答案】BD
【详解】对选项A:函数的值域为,则,
解得或,正确;
对选项B:,
当且仅当,即时等号成立,等号成立条件不满足,错误;
对选项C:,即,
函数单调递增,故,即;
取满足,不成立,正确;
对选项D:当时,不等式恒成立,错误;
12.【答案】AC
【详解】由于函数是定义在上的奇函数,所以讨论情况如下:
作图像如下图所示,
关于的方程,
解得或
由于与图像有一个公共点,
则图像与图像有三个公共点,如图所示,,
同理,时,,所以实数的值是.
三 填空题
13.【答案】
【详解】由题得,,且,
所以,
,当且仅当时等号成立.
14.【答案】
【详解】函数的定义域满足:,
解得且.
故答案为:.
15.【答案】
【详解】由题意得,
则或,
又,即,解得或(舍去),
则,
所以
.
故答案为:.
16.【答案】
【解析】因为函数满足,所以函数的图象关于直线成轴对称,
因为当时,,由,则,即,
所以在上单调递增,则在上单调递减,
由,
由,根据函数在上单调递增,则;
由,根据函数在上单调递增,则.
由函数在上单调递减,则,即.
四 解答题
17.【答案】(1);(2)
【详解】(1)
.
(2)由不等式的解集为,得,解答
则,即,解得,即原不等式的解集为.
18.【答案】(1)2;(2).
【详解】(1)由已知,
化简得,整理得故
(2)
.
19.【答案】(1);(2
【详解】(1)由,即,
所以,解得,所以,
因为,
当时,,解得,
当时,或,
解得或,
综上可得实数的取值范围为.
(2)是的充分条件,,
,解得或,
即实数的取值集合为.
20.【答案】(1)
(2)时有最小值,最小值为.
【详解】(1)由题可先写出速度关于时间的函数,
代入与公式可得
解得;
(2)①稳定阶段中单调递减,此过程中最小值;
②疲劳阶段,
则有,
当且仅当,即时,“成立,
所以疲劳阶段中体力最低值为,
由于,因此,在时,运动员体力有最小值.
21.【答案】(1);(2)
解:(1)为奇函数,所以,
则由,得,得,
故函数在上单调递增.
则
解得,故不等式的解集为.
(2)因为,所以.
若对所有恒成立,
则成立,且,
所以对恒成立,即对恒成立.
令,
则即得
解得
故实数的取值范围是.
22.【答案】(1)
(2)证明见解析(3)证明见解析
【解析】
(1)函数的单调递减区间为,故,,
函数定义域满足:,解得或,
在上单调递增,在上单调递增,
故函数的单调递增区间为;
(2),即,即,
设,函数在上单调递增,
,故在上有唯一零点,
即方程在内有且仅有一个根;
(3),要证,即,函数在上单调递增,
故,即,得证.
同课章节目录
