等式的性质(浙江省台州市仙居县)
文档属性
| 名称 | 等式的性质(浙江省台州市仙居县) |
|
|
| 格式 | rar | ||
| 文件大小 | 38.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-07 00:00:00 | ||
图片预览






文档简介
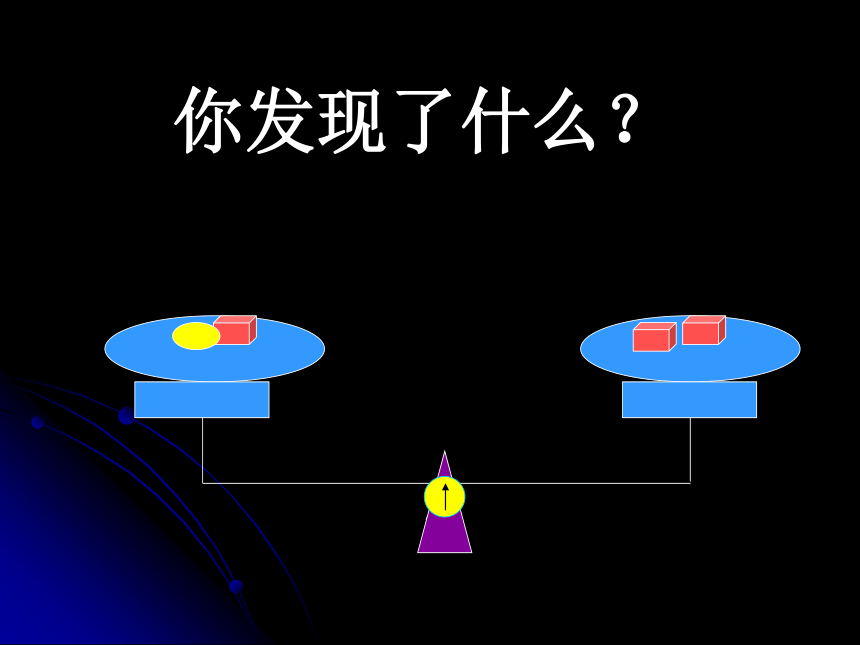
课件22张PPT。2.1.2等式的性质(1)第三章一元一次方程仙居外语学校
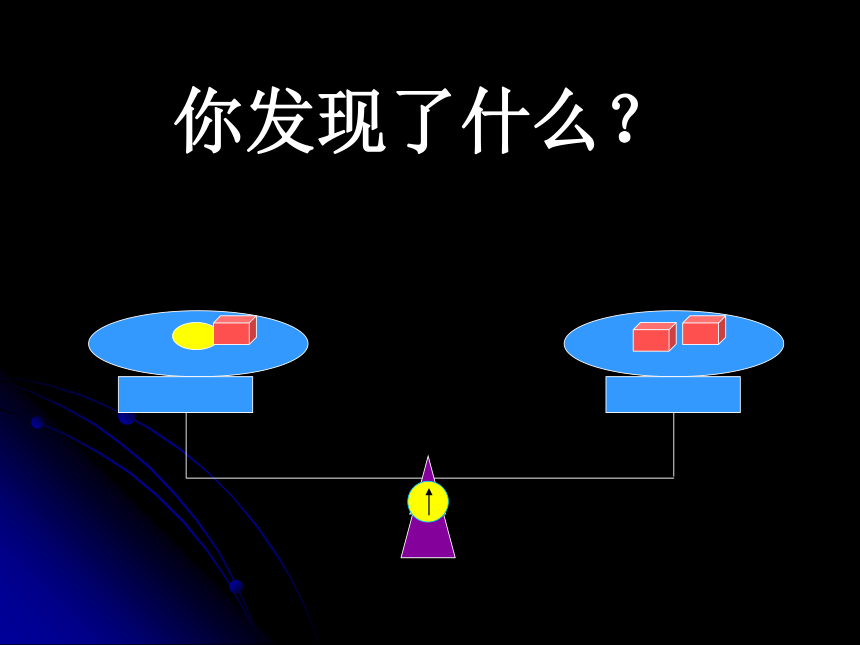
学习目标:1.了解等式的两条性质2.会用等式的性质解简单的一元一次方程(学会检验方程的解) 估计方程的解:你发现了什么?你发现了什么?等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式这里的a,b,c可以是具体的一个数,也可以是一个代数式。例题1:解方程: x–7=5x=?两边同加上7分析:解方程: x–7=5解:方程两边都加上7,得 x–7+7=5+7即:
x=5+7
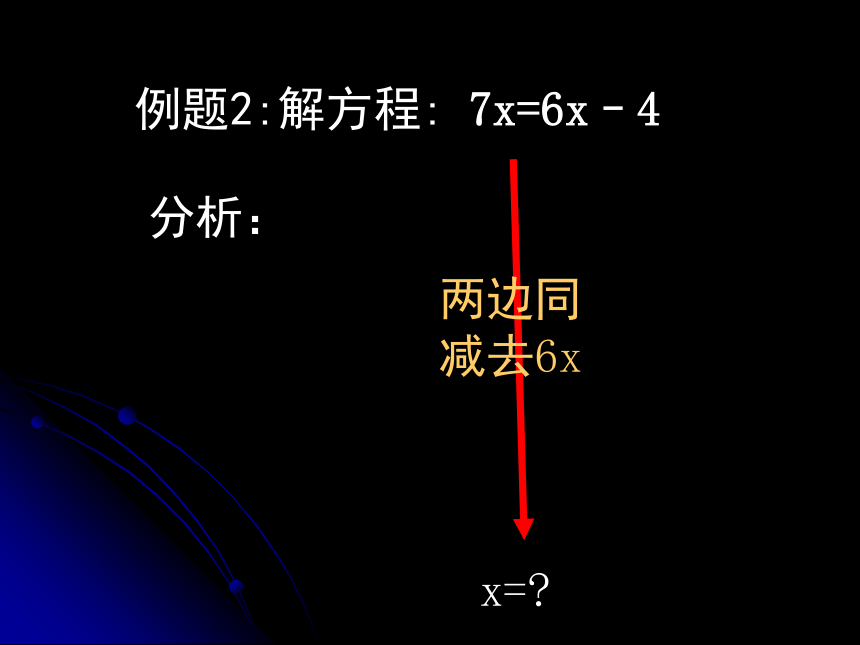
x=12检验:把x=12代入原方程得, 左边=12–7=5,右边=5 左边=右边 ∴x=12是原方程的解。 例题2:解方程: 7x=6x–4x=?两边同减去6x分析:解方程:7x=6x–4 两边同减去6x,得 7x–6x=6x–4-6x合并同类项,得
x =–4 检验:把x=–4代入原方程得, 左边=7x(– 4)=-28,
右边=6x(– 4)– 4= –28
左边=右边
∴ x= – 4是原方程的解解:练习一下:利用等式性质1解下列方程,并写出检验
(1) 3x=2x+5 (2) 7x–3=6x-2探求新知×3÷ 3如:2=2 那么2× 3=2×3
如:6=6 那么6÷2=6÷2
等式性质2 等式两边同时乘一个数,或除以同一个不为0数,结果仍相等.我思考 我进步如果a=b,那么ac=____
如果a= b(c≠0),那么 =____bc这里的a,b,c可以是具体的一个数,也可以是一个代数式。新知运用例 利用等式的性质解下列方程:
(2)3x-5=22
(3)4x+7=6x-3
(4)
知识小结1:请你归纳一下解一元一次方程的依据是什么?
2:解一元一次方程的结果形式是什么?练习:下面的解方程对不对?如果不对,错在哪里?应当怎样改正?
(1)从7+x=13,得到x=13+7 (2)从5x=4x+8,得到5x–4x=8 (3)从3x=8-2x,得3x+2x=-8 χ改:从7+x=13,得到x=13–7? χ 改:从3x=8-2x 得 3x+2x=8巩固练习:练习:小明在解方程x–4=7时,是这样写解的过程的:
x–4=7=x=7+4=x=11
(1)小明这样写对不对?
(2)应该怎样写?×二、选择填空(3)如果 ,那么下列等式中一定成立
的是( ) 快乐练习D1 已知方程a-2x= -4的解为x=4,求式子a3-a2-a的值。提高探究超越自我2 解方程:|2x|=3x-5练习2、解下列方程,并写出检验过程 (1)x+11=38 (2)7+x=5 (3)12x-1=11x (4)9+11x=10x-7巩固练习:本节小结本节课我们学习了什么知识?
解方程的依据是什么?移项应该注意什么?作业:作业本(2)
学习目标:1.了解等式的两条性质2.会用等式的性质解简单的一元一次方程(学会检验方程的解) 估计方程的解:你发现了什么?你发现了什么?等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式这里的a,b,c可以是具体的一个数,也可以是一个代数式。例题1:解方程: x–7=5x=?两边同加上7分析:解方程: x–7=5解:方程两边都加上7,得 x–7+7=5+7即:
x=5+7
x=12检验:把x=12代入原方程得, 左边=12–7=5,右边=5 左边=右边 ∴x=12是原方程的解。 例题2:解方程: 7x=6x–4x=?两边同减去6x分析:解方程:7x=6x–4 两边同减去6x,得 7x–6x=6x–4-6x合并同类项,得
x =–4 检验:把x=–4代入原方程得, 左边=7x(– 4)=-28,
右边=6x(– 4)– 4= –28
左边=右边
∴ x= – 4是原方程的解解:练习一下:利用等式性质1解下列方程,并写出检验
(1) 3x=2x+5 (2) 7x–3=6x-2探求新知×3÷ 3如:2=2 那么2× 3=2×3
如:6=6 那么6÷2=6÷2
等式性质2 等式两边同时乘一个数,或除以同一个不为0数,结果仍相等.我思考 我进步如果a=b,那么ac=____
如果a= b(c≠0),那么 =____bc这里的a,b,c可以是具体的一个数,也可以是一个代数式。新知运用例 利用等式的性质解下列方程:
(2)3x-5=22
(3)4x+7=6x-3
(4)
知识小结1:请你归纳一下解一元一次方程的依据是什么?
2:解一元一次方程的结果形式是什么?练习:下面的解方程对不对?如果不对,错在哪里?应当怎样改正?
(1)从7+x=13,得到x=13+7 (2)从5x=4x+8,得到5x–4x=8 (3)从3x=8-2x,得3x+2x=-8 χ改:从7+x=13,得到x=13–7? χ 改:从3x=8-2x 得 3x+2x=8巩固练习:练习:小明在解方程x–4=7时,是这样写解的过程的:
x–4=7=x=7+4=x=11
(1)小明这样写对不对?
(2)应该怎样写?×二、选择填空(3)如果 ,那么下列等式中一定成立
的是( ) 快乐练习D1 已知方程a-2x= -4的解为x=4,求式子a3-a2-a的值。提高探究超越自我2 解方程:|2x|=3x-5练习2、解下列方程,并写出检验过程 (1)x+11=38 (2)7+x=5 (3)12x-1=11x (4)9+11x=10x-7巩固练习:本节小结本节课我们学习了什么知识?
解方程的依据是什么?移项应该注意什么?作业:作业本(2)
