第23章 解直角三角形 单元检测题 2023-2024学年沪科版九年级数学 上册(含答案)
文档属性
| 名称 | 第23章 解直角三角形 单元检测题 2023-2024学年沪科版九年级数学 上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 588.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 21:28:35 | ||
图片预览


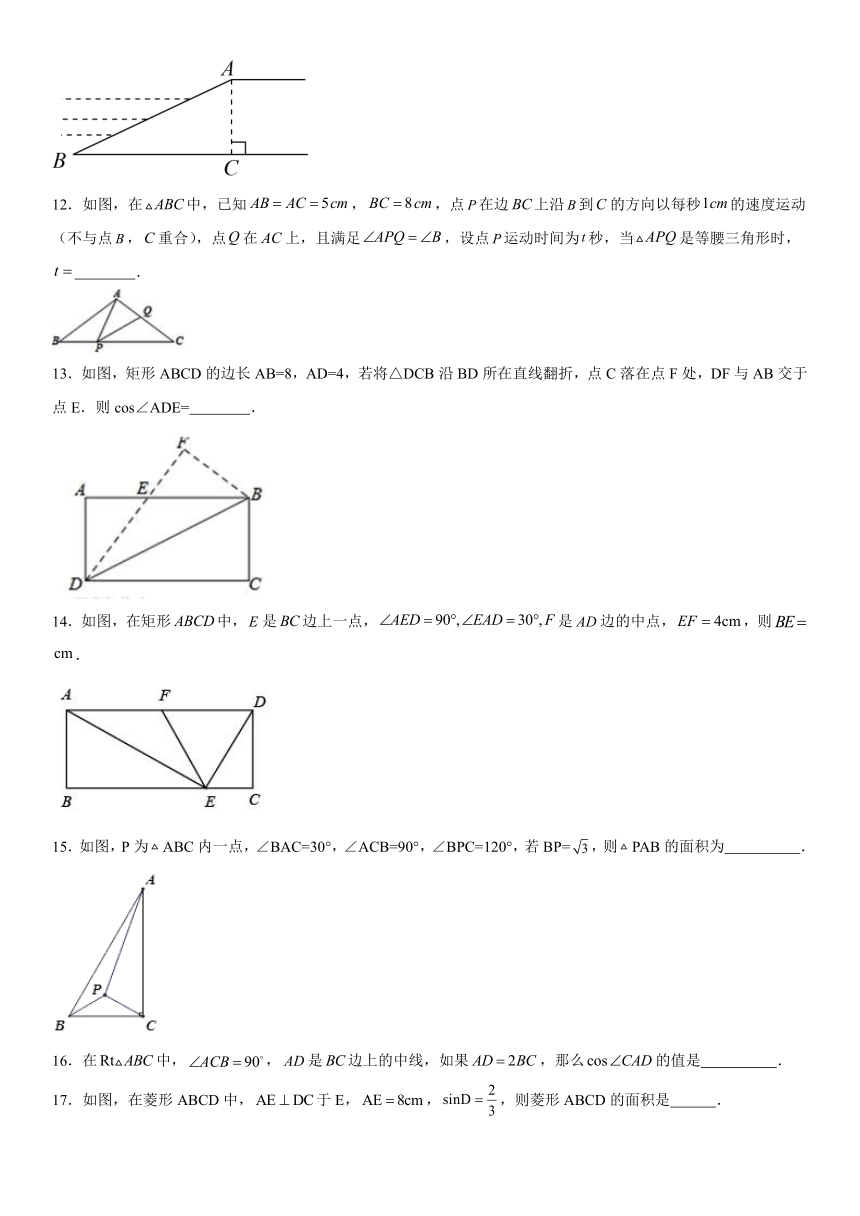
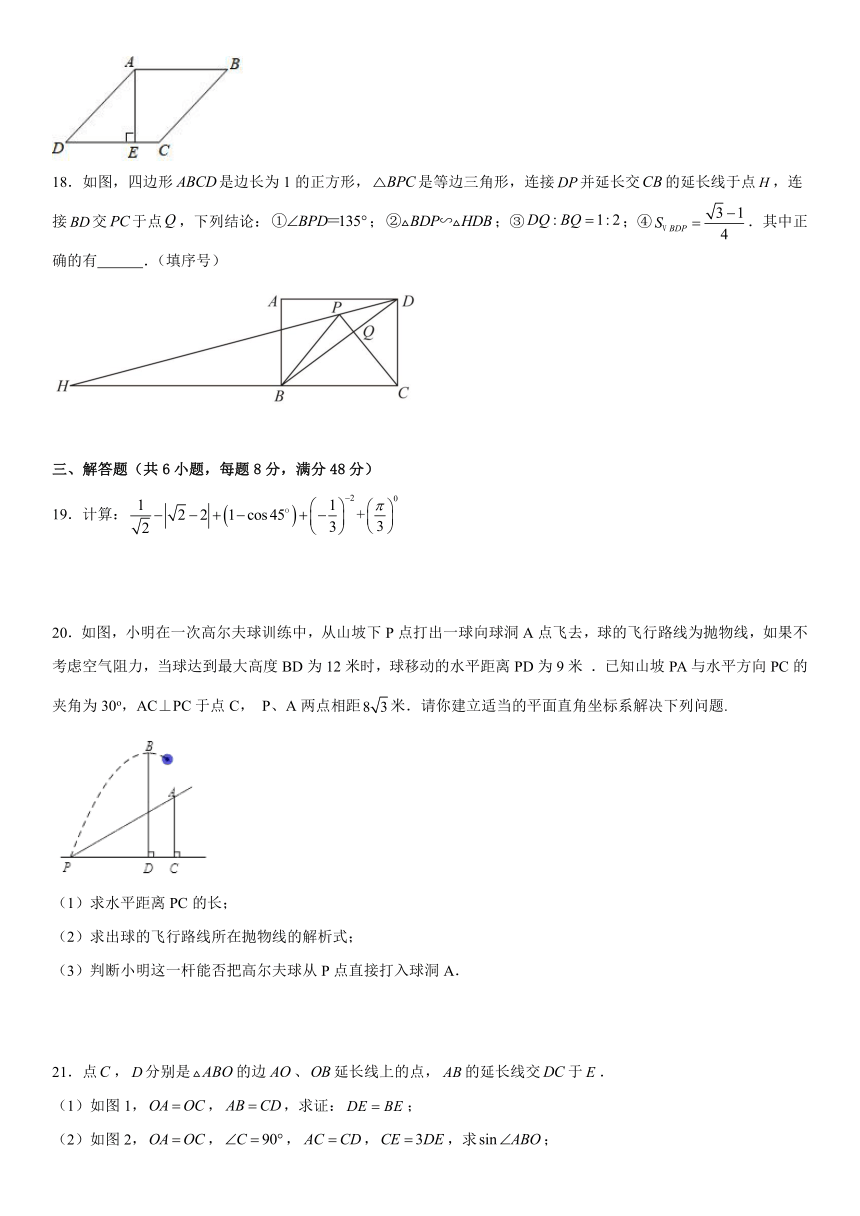
文档简介
第23章《解直角三角形》单元检测题
2023-2024学年九年级上册数学沪科版
一、单选题(共10小题,满分40分)
1.在中,如果各边长度都扩大2倍,则锐角的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
2.如图,某超市自动扶梯的倾斜角为,扶梯长为米,则扶梯高的长为( )
A.米 B. 米 C. 米 D.米
3.在RtABC中,,那么下列结论正确的是( )
A. B. C. D.
4.在中,,,( )
A. B. C. D.
5.如图,在中,,,AB=5,则AC的长为( )
A.3 B.4 C. D.
6.如图,在中,.现分别以、、为边长在边同侧构造正方形,正方形,正方形,点D、E均落在上,交于M.已知阴影部分的面积为48,,则的值为( )
A. B. C. D.
7.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2 ,AB=4,则tan∠BCD的值为( )
A. B. C. D.
8.如图,是斜靠在墙上的长梯,是梯上一点,梯脚与墙脚的距离为(即的长),点与墙的距离为(即的长),长为,则梯子的长为( )
A. B. C. D.
9.已知正ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
A. B. C. D.
10.如图,在平行四边形ABCD中,,,,E、F是BC、CD边上点,且,,AE 、AF分别交BD于点M,N,则MN的长度是( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.某河堤横断面如图所示,提高米,迎水坡AB的坡比是,则AB的长为 .
12.如图,在中,已知,,点在边上沿到的方向以每秒的速度运动(不与点,重合),点在上,且满足,设点运动时间为秒,当是等腰三角形时, .
13.如图,矩形ABCD的边长AB=8,AD=4,若将△DCB沿BD所在直线翻折,点C落在点F处,DF与AB交于点E.则cos∠ADE= .
14.如图,在矩形中,是边上一点,是边的中点,,则 .
15.如图,P为ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°,若BP=,则PAB的面积为 .
16.在中,,是边上的中线,如果,那么的值是 .
17.如图,在菱形ABCD中,于E,,,则菱形ABCD的面积是 .
18.如图,四边形是边长为1的正方形,是等边三角形,连接并延长交的延长线于点,连接交于点,下列结论:;;③;④.其中正确的有 .(填序号)
三、解答题(共6小题,每题8分,满分48分)
19.计算:+
20.如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为12米时,球移动的水平距离PD为9米 .已知山坡PA与水平方向PC的夹角为30o,AC⊥PC于点C, P、A两点相距米.请你建立适当的平面直角坐标系解决下列问题.
(1)求水平距离PC的长;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从P点直接打入球洞A.
21.点,分别是的边、延长线上的点,的延长线交于.
(1)如图1,,,求证:;
(2)如图2,,,,,求;
(3)如图3,若,,,求的长.
22.如图①,直线与轴、轴分别交于两点,将沿轴正方向平移后,点、点的对应点分别为点、点,且四边形为菱形,连接,抛物线经过三点,点为上方抛物线上一动点,作,垂足为
求此抛物线的函数关系式;
求线段长度的最大值;
如图②,延长交轴于点,连接,若为等腰三角形,请直接写出点的坐标.
23.如图,已知,,反比例函数的图象过点,反例函数的图象过点A.
(1)求a和k的值;
(2)过点B作轴,与双曲线交于点C,求的面积.
24.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
①求证:=;
②若CE=1且AE=DE+2CE,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
参考答案:
1.A
2.A
3.B
4.B
5.D
6.B
7.B
8.B
9.D
10.B
11.
12.秒或秒
13.
14.6
15.
16.
17.
18.①②④
19.9+
20.(1)12m;(2);(3)不能
21.(1)略;(2);(3)6
22.(1);(2)最大值为.(3)点P的坐标为或
23.(1)
(2)
24.tanα+tanβ=
2023-2024学年九年级上册数学沪科版
一、单选题(共10小题,满分40分)
1.在中,如果各边长度都扩大2倍,则锐角的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
2.如图,某超市自动扶梯的倾斜角为,扶梯长为米,则扶梯高的长为( )
A.米 B. 米 C. 米 D.米
3.在RtABC中,,那么下列结论正确的是( )
A. B. C. D.
4.在中,,,( )
A. B. C. D.
5.如图,在中,,,AB=5,则AC的长为( )
A.3 B.4 C. D.
6.如图,在中,.现分别以、、为边长在边同侧构造正方形,正方形,正方形,点D、E均落在上,交于M.已知阴影部分的面积为48,,则的值为( )
A. B. C. D.
7.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2 ,AB=4,则tan∠BCD的值为( )
A. B. C. D.
8.如图,是斜靠在墙上的长梯,是梯上一点,梯脚与墙脚的距离为(即的长),点与墙的距离为(即的长),长为,则梯子的长为( )
A. B. C. D.
9.已知正ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
A. B. C. D.
10.如图,在平行四边形ABCD中,,,,E、F是BC、CD边上点,且,,AE 、AF分别交BD于点M,N,则MN的长度是( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.某河堤横断面如图所示,提高米,迎水坡AB的坡比是,则AB的长为 .
12.如图,在中,已知,,点在边上沿到的方向以每秒的速度运动(不与点,重合),点在上,且满足,设点运动时间为秒,当是等腰三角形时, .
13.如图,矩形ABCD的边长AB=8,AD=4,若将△DCB沿BD所在直线翻折,点C落在点F处,DF与AB交于点E.则cos∠ADE= .
14.如图,在矩形中,是边上一点,是边的中点,,则 .
15.如图,P为ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°,若BP=,则PAB的面积为 .
16.在中,,是边上的中线,如果,那么的值是 .
17.如图,在菱形ABCD中,于E,,,则菱形ABCD的面积是 .
18.如图,四边形是边长为1的正方形,是等边三角形,连接并延长交的延长线于点,连接交于点,下列结论:;;③;④.其中正确的有 .(填序号)
三、解答题(共6小题,每题8分,满分48分)
19.计算:+
20.如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为12米时,球移动的水平距离PD为9米 .已知山坡PA与水平方向PC的夹角为30o,AC⊥PC于点C, P、A两点相距米.请你建立适当的平面直角坐标系解决下列问题.
(1)求水平距离PC的长;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从P点直接打入球洞A.
21.点,分别是的边、延长线上的点,的延长线交于.
(1)如图1,,,求证:;
(2)如图2,,,,,求;
(3)如图3,若,,,求的长.
22.如图①,直线与轴、轴分别交于两点,将沿轴正方向平移后,点、点的对应点分别为点、点,且四边形为菱形,连接,抛物线经过三点,点为上方抛物线上一动点,作,垂足为
求此抛物线的函数关系式;
求线段长度的最大值;
如图②,延长交轴于点,连接,若为等腰三角形,请直接写出点的坐标.
23.如图,已知,,反比例函数的图象过点,反例函数的图象过点A.
(1)求a和k的值;
(2)过点B作轴,与双曲线交于点C,求的面积.
24.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
①求证:=;
②若CE=1且AE=DE+2CE,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
参考答案:
1.A
2.A
3.B
4.B
5.D
6.B
7.B
8.B
9.D
10.B
11.
12.秒或秒
13.
14.6
15.
16.
17.
18.①②④
19.9+
20.(1)12m;(2);(3)不能
21.(1)略;(2);(3)6
22.(1);(2)最大值为.(3)点P的坐标为或
23.(1)
(2)
24.tanα+tanβ=
