第四章 图形的相似单元测试题( 2 )(含答案)2023-2024学年北师大版九年级数学上册
文档属性
| 名称 | 第四章 图形的相似单元测试题( 2 )(含答案)2023-2024学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 169.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 08:10:50 | ||
图片预览



文档简介
2023-2024学年北师大版数学九年级上册单元测试题【图形的相似】2(含答案)
选择题(每小题3分,10小题,共30分)
1、如图,在△ABC中.∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A、1对 B、2对 C、3对 D、4对
2、如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是( )
A、 B、 C、 D、
3、如图,身高为1.6米的某同学想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( )
A、6.4米 B、7.0米 C、8.0米 D、9.0米
4、一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,且最短边长为6,则最长边长为( )
A、18 B、12 C、24 D、30
5、线段4cm、16cm的比例中项为( )
A、20cm B、64cm C、±8cm D、8cm
6、如果两个相似三角形的相似比是1:7,则它们的面积比等于( )
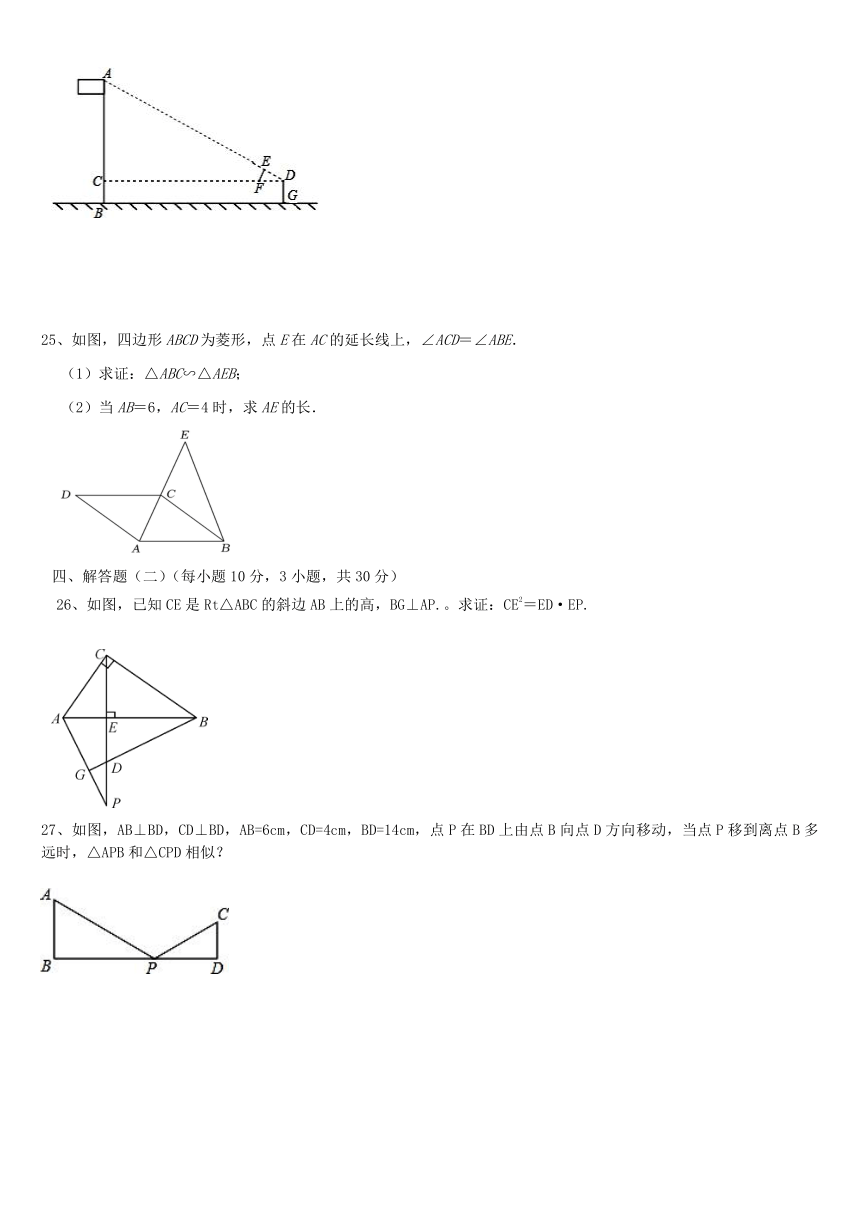
A、1: B、1:7 C、1:3.5 D、1:49
7、比例尺为1:1000的图纸上某区域面积400cm2 , 则实际面积为( )
A、 B、 C、 D、
8、如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
A、 B、 C、 D、
9、如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )
A、2 B、4 C、8 D、1
10、如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
A、△PAB∽△PCA B、△PAB∽△PDA C、△ABC∽△DBA D、△ABC∽△DCA
填空题(每小题3分,10小题,共30分)
11、如图,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是________ 。
12、若 , 则的值等于________。
13、如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为________。
14、两个相似多边形最长的的边分为10cm和25cm,它们的周长之差为60cm,则这两个多边形的周长分别为_______
15、如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于________。
16、在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为________米。
17、如图,已知∠1=∠2,现给出如下条件:①∠D=∠B;②∠E=∠C; ③;④
则其中能说明△ABC∽△ADE的是________(填序号)
18、两个相似三角形面积之比为2:7,较大三角形一边上的高为,则较小三角形的对应边上的高为______。
19、如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=________ 。
20、经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为________ 。
解答题(一)(每小题6分,5小题,共30分)
21、已知a、b、c是△ABC的三边长,且==≠0,求:(1)的值.(2)若△ABC的周长为90,求各边的长.
22、如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;(2)若AB=12,AD=8,CD=15,求DB的长.
23、如图,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.
(1)求∠ACB的度数;(2)求CD的长.
24、如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
25、如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
(2)当AB=6,AC=4时,求AE的长.
解答题(二)(每小题10分,3小题,共30分)
26、如图,已知CE是Rt△ABC的斜边AB上的高,BG⊥AP.。求证:CE2=ED·EP.
27、如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
28、如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP
交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC
2023-2024学年北师大版数学九年级上册单元测试题【图形的相似】2答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D D B C A C
填空题
题号 11 12 13 14 15 16 17 18 19 20
答案 1∶3 2.4 100cm;40cm 90 ①②③ 4.5 113°或92°
解答题(一)
21、解:⑴设
∴
⑵设
∴
∴
∴
22、⑴证明:∵AD∥BC
∴∠ADB=∠DBC
∵∠A=∠BDC.
∴△ABD∽△DCB
⑵、由⑴知△ABD∽△DCB
∴
∵AB=12,AD=8,CD=15,
∴
∴DB=10
23、解:⑴∵△ABC∽△DAC
∴∠BAC=∠D
∵∠D=117°
∴∠BAC=117°
∵∠B=36°
∴∠ACB=180°-∠B-∠BAC
=180°-36°-117°
=27°
⑵∵△ABC∽△DAC
∴
∵AC=4,BC=6
∴
∴
24、解:由题意可得:△DEF∽△DCA,
则,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
答:旗杆的高度为11.5m.
25、⑴∵四边形ABCD为菱形
∴CD∥AB,BC=AB
∴∠ACD=∠BAC,∠ACB=∠BAC
∵∠ACD=∠ABE
∴∠ACB=∠BAC=∠ABE
∴△ABC∽△AEB;
⑵∵△ABC∽△AEB;
∴
∵AB=6,AC=4
∴
∴AE=9
四、解答题(二)
26、证明:∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE.
∴=,
即CE2=AE·BE.
∵CE⊥AB,BG⊥AP,
∴∠EBD+∠EDB=∠P+∠GDP=90°.
∴∠EBD=∠P.
∴△AEP∽△DEB.
∴=,
即AE·EB=ED·EP.
∴CE2=ED·EP.
27、解:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当时,△PAB与△PCD是相似三角形,
∵AB=6cm,CD=4cm,BD=14cm,
∴
解得:BP=2或12或,
即BP=2或12或时,△PAB与△PCD是相似三角形.
28、解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴∠APQ=∠CDQ.
又∵∠AQP=∠CQD,
∴△APQ∽△CDQ.
(2)当t=5时,DP⊥AC.
理由:∵t=5,∴AP=5.
∴=.
又∵=,
∴=.
又∵∠PAD=∠ADC=90°,
∴△PAD∽△ADC.
∴∠ADP=∠DCA.
∵∠ADP+∠CDP=∠ADC=90°,
∴∠DCA+∠CDP=90°.
∴∠DQC=90°,即DP⊥AC.
选择题(每小题3分,10小题,共30分)
1、如图,在△ABC中.∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A、1对 B、2对 C、3对 D、4对
2、如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是( )
A、 B、 C、 D、
3、如图,身高为1.6米的某同学想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( )
A、6.4米 B、7.0米 C、8.0米 D、9.0米
4、一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,且最短边长为6,则最长边长为( )
A、18 B、12 C、24 D、30
5、线段4cm、16cm的比例中项为( )
A、20cm B、64cm C、±8cm D、8cm
6、如果两个相似三角形的相似比是1:7,则它们的面积比等于( )
A、1: B、1:7 C、1:3.5 D、1:49
7、比例尺为1:1000的图纸上某区域面积400cm2 , 则实际面积为( )
A、 B、 C、 D、
8、如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
A、 B、 C、 D、
9、如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )
A、2 B、4 C、8 D、1
10、如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
A、△PAB∽△PCA B、△PAB∽△PDA C、△ABC∽△DBA D、△ABC∽△DCA
填空题(每小题3分,10小题,共30分)
11、如图,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是________ 。
12、若 , 则的值等于________。
13、如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为________。
14、两个相似多边形最长的的边分为10cm和25cm,它们的周长之差为60cm,则这两个多边形的周长分别为_______
15、如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于________。
16、在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为________米。
17、如图,已知∠1=∠2,现给出如下条件:①∠D=∠B;②∠E=∠C; ③;④
则其中能说明△ABC∽△ADE的是________(填序号)
18、两个相似三角形面积之比为2:7,较大三角形一边上的高为,则较小三角形的对应边上的高为______。
19、如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=________ 。
20、经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为________ 。
解答题(一)(每小题6分,5小题,共30分)
21、已知a、b、c是△ABC的三边长,且==≠0,求:(1)的值.(2)若△ABC的周长为90,求各边的长.
22、如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;(2)若AB=12,AD=8,CD=15,求DB的长.
23、如图,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.
(1)求∠ACB的度数;(2)求CD的长.
24、如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
25、如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
(2)当AB=6,AC=4时,求AE的长.
解答题(二)(每小题10分,3小题,共30分)
26、如图,已知CE是Rt△ABC的斜边AB上的高,BG⊥AP.。求证:CE2=ED·EP.
27、如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
28、如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP
交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC
2023-2024学年北师大版数学九年级上册单元测试题【图形的相似】2答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D D B C A C
填空题
题号 11 12 13 14 15 16 17 18 19 20
答案 1∶3 2.4 100cm;40cm 90 ①②③ 4.5 113°或92°
解答题(一)
21、解:⑴设
∴
⑵设
∴
∴
∴
22、⑴证明:∵AD∥BC
∴∠ADB=∠DBC
∵∠A=∠BDC.
∴△ABD∽△DCB
⑵、由⑴知△ABD∽△DCB
∴
∵AB=12,AD=8,CD=15,
∴
∴DB=10
23、解:⑴∵△ABC∽△DAC
∴∠BAC=∠D
∵∠D=117°
∴∠BAC=117°
∵∠B=36°
∴∠ACB=180°-∠B-∠BAC
=180°-36°-117°
=27°
⑵∵△ABC∽△DAC
∴
∵AC=4,BC=6
∴
∴
24、解:由题意可得:△DEF∽△DCA,
则,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
答:旗杆的高度为11.5m.
25、⑴∵四边形ABCD为菱形
∴CD∥AB,BC=AB
∴∠ACD=∠BAC,∠ACB=∠BAC
∵∠ACD=∠ABE
∴∠ACB=∠BAC=∠ABE
∴△ABC∽△AEB;
⑵∵△ABC∽△AEB;
∴
∵AB=6,AC=4
∴
∴AE=9
四、解答题(二)
26、证明:∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE.
∴=,
即CE2=AE·BE.
∵CE⊥AB,BG⊥AP,
∴∠EBD+∠EDB=∠P+∠GDP=90°.
∴∠EBD=∠P.
∴△AEP∽△DEB.
∴=,
即AE·EB=ED·EP.
∴CE2=ED·EP.
27、解:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当时,△PAB与△PCD是相似三角形,
∵AB=6cm,CD=4cm,BD=14cm,
∴
解得:BP=2或12或,
即BP=2或12或时,△PAB与△PCD是相似三角形.
28、解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴∠APQ=∠CDQ.
又∵∠AQP=∠CQD,
∴△APQ∽△CDQ.
(2)当t=5时,DP⊥AC.
理由:∵t=5,∴AP=5.
∴=.
又∵=,
∴=.
又∵∠PAD=∠ADC=90°,
∴△PAD∽△ADC.
∴∠ADP=∠DCA.
∵∠ADP+∠CDP=∠ADC=90°,
∴∠DCA+∠CDP=90°.
∴∠DQC=90°,即DP⊥AC.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
