1.3.1柱体 锥体 台体的表面积与体积
文档属性
| 名称 | 1.3.1柱体 锥体 台体的表面积与体积 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-19 20:16:06 | ||
图片预览






文档简介
课件37张PPT。1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积瞧,多么宏伟壮观的金字塔!这将需要多少沙石?1.了解柱体、锥体、台体的表面积和体积公式的推导过程.(难点)
2.能运用公式求解柱体、锥体和台体的表面积与体积.(重点)
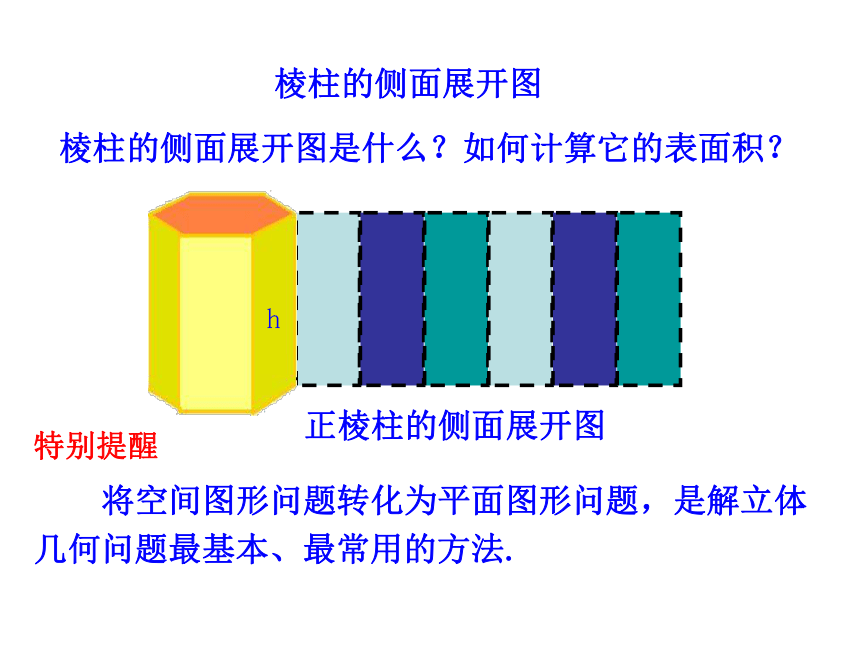
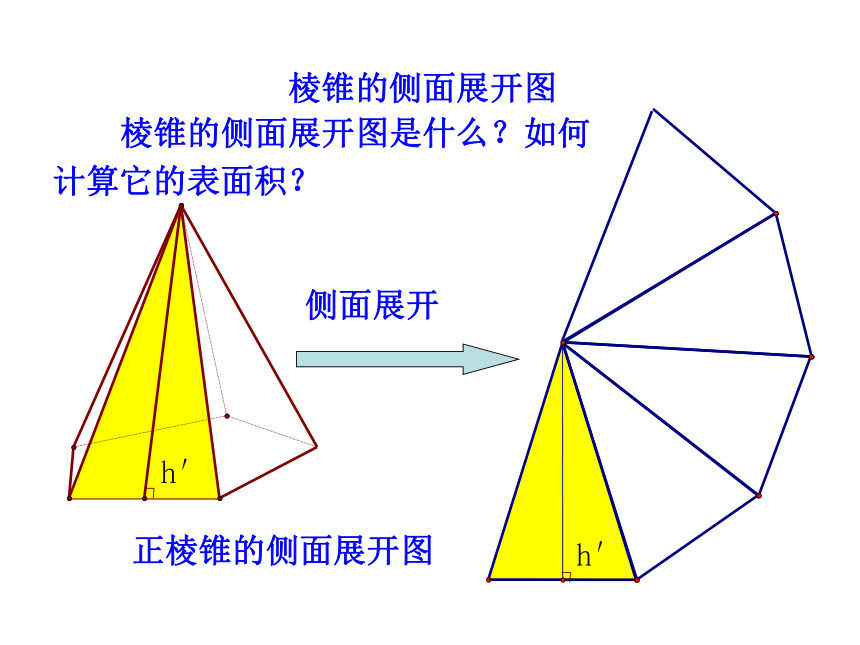
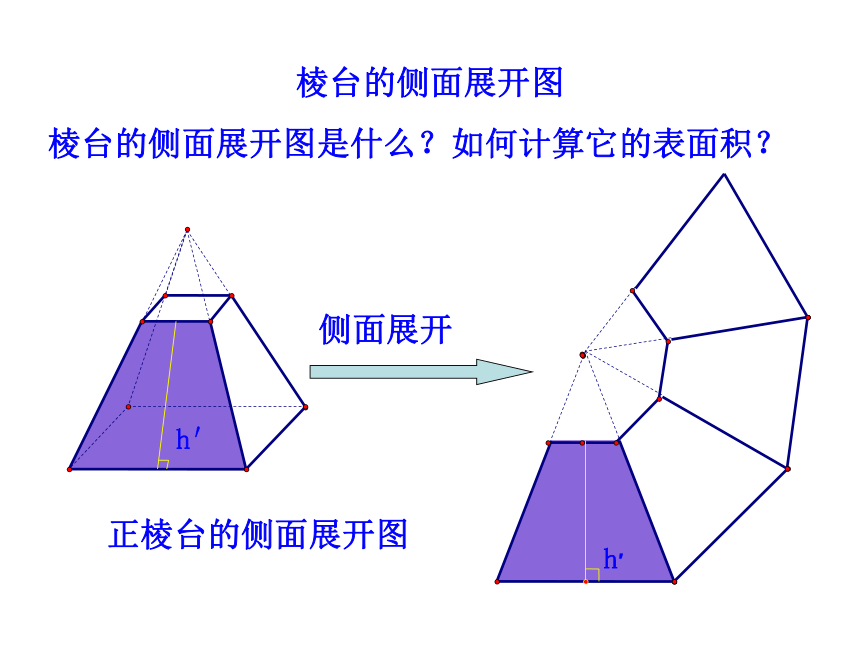
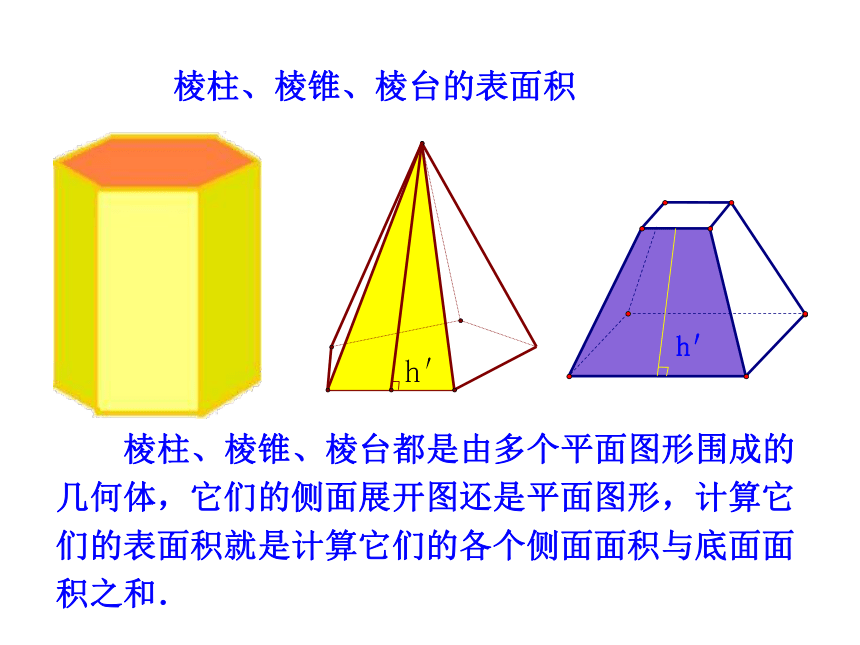
3. 熟悉台体与柱体和锥体之间的转换关系,培养转化与化归的思想与空间想象能力. (难点)几何体表面积展开图平面图形面积 在初中已经学过了正方体和长方体的表面积,以及它们的展开图,你知道正方体和长方体的展开图与其表面积的关系吗? 正方体、长方体是由多个平面图形围成的多面体,它们的表面积就是各个面的面积的和,也就是展开图的面积. 一般地,我们可以把多面体展成平面图形,利用平面图形求面积的方法,求多面体的表面积. 棱柱、棱锥、棱台都是由多个平面图形围成的多面体,它们的展开图是什么?如何计算它们的表面积?知识探究棱柱的侧面展开图是什么?如何计算它的表面积?h棱柱的侧面展开图正棱柱的侧面展开图 将空间图形问题转化为平面图形问题,是解立体几何问题最基本、最常用的方法.特别提醒 棱锥的侧面展开图是什么?如何计算它的表面积?侧面展开正棱锥的侧面展开图棱锥的侧面展开图棱台的侧面展开图是什么?如何计算它的表面积?棱台的侧面展开图侧面展开正棱台的侧面展开图棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它们的各个侧面面积与底面面积之和.例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.分析:四面体的展开图是由四个全等的等边三角形组成.因为BC=a,所以因此,四面体S-ABC 的表面积为交BC于点D.【解析】先求△SBC的面积,过点S作知识应用圆柱的表面积圆柱的侧面展开图是一个矩形,圆锥的表面积圆锥的侧面展开图是一个扇形,S圆台的表面积 参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么?圆台的侧面展开图是一个扇环,圆柱、圆锥、圆台三者的表面积公式之间有什么关系?【提升总结】知识应用
例2 如图,一个圆台形花盆盆口直径为20 cm,盆底直径为15 cm,底部渗水圆孔直径为1.5 cm,盆壁长15 cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100 毫升油漆,涂100个这样的花盆需要多少油漆(π取3.14,结果精确到1 毫升,可用计算器)?分析:只要求出每一个花盆外壁的表面积,就可求出油漆的用量.而花盆外壁的表面积等于花盆的侧面面积加上底面面积,再减去底面圆孔的面积.涂100个花盆需油漆:
0.1×100×100=1000(毫升).
答:涂100个这样的花盆约需要1000毫升油漆.【解析】如图,由圆台的表面积公式得一个花盆外壁的表面积 以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式.它们的体积公式可以统一为(S为底面面积,h为高).柱体体积一般柱体的体积也是其中S为底面面积,h为柱体的高.圆锥的体积公式是(其中S为底面面积,h为高),它的体积是同底等高的圆柱的体积的 .圆锥体积探究棱锥与同底等高的棱柱体积之间的关系.棱锥体积三棱锥与同底等高的三棱柱的关系等底等高的三棱锥体积相等.(其中S为底面面积,h为高). 由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是底面面积乘高的 . 经过探究得知,棱锥也是同底等高的棱柱体积
的 ,即棱锥的体积台体体积由于圆台(棱台)是由圆锥(棱锥)截成的,因此可以利用两个锥体的体积差,得到圆台(棱台)的体积公式(过程略)根据台体的特征,如何求台体的体积?棱台(圆台)的体积公式 其中 , 分别为上、下底面面积,h为棱台(圆台)的高. 分别为上、下底面面积,h 为台体高S为底面面积,
h为锥体高S为底面面积,
h为柱体高柱体、锥体、台体的体积公式之间有什么关系?公式有它的统一性.【提升总结】例3 有一堆规格相同的铁制(铁的密度是7.8 g/cm3)六角螺帽共重5.8 kg,已知底面是正六边形,边长为12 mm,内孔直径为10 mm,高为10 mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?知识应用【解析】六角螺帽的体积是六棱柱体积与圆柱体积的差,即所以螺帽的个数为5.8×1000÷(7.8×2.956)≈
252(个).答:这堆螺帽大约有252个.1.一个棱锥的三视图如图,则该棱锥的表面积为( )A.48+ B.48+
C.36+ D.36+A【解析】选A.由三视图得棱锥如图所示,
AO⊥底面BCD,O是BD的中点,BC=CD=6,
BC⊥CD,AO=4,AB=AD.
S△BCD= ×6×6=18,
S△ABD= ×6 ×4=12 .
取BC的中点E,连接AE,OE.
可得BC⊥AE,AE=
所以S△ABC=S△ACD= ×6×5=15,
所以S全=18+12 +15+15=48+12 .2.(2012·新课标全国卷)如图所示:
网格纸上小正方形的边长为1,
粗线画出的是某几何体的三视
图,则此几何体的体积为( )
A.6 B.9
C.12 D.18
【解析】选B.由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S= , BD5.(2012·上海高考)若一个圆锥的侧面展开图是面积
为2?的半圆面,则该圆锥的体积为_________ .
柱体、锥体、台体的表面积 圆台 圆柱 圆锥转化的思想柱体、锥体、台体的体积锥体台体柱体联系的观点 不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
1.3.1 柱体、锥体、台体的表面积与体积瞧,多么宏伟壮观的金字塔!这将需要多少沙石?1.了解柱体、锥体、台体的表面积和体积公式的推导过程.(难点)
2.能运用公式求解柱体、锥体和台体的表面积与体积.(重点)
3. 熟悉台体与柱体和锥体之间的转换关系,培养转化与化归的思想与空间想象能力. (难点)几何体表面积展开图平面图形面积 在初中已经学过了正方体和长方体的表面积,以及它们的展开图,你知道正方体和长方体的展开图与其表面积的关系吗? 正方体、长方体是由多个平面图形围成的多面体,它们的表面积就是各个面的面积的和,也就是展开图的面积. 一般地,我们可以把多面体展成平面图形,利用平面图形求面积的方法,求多面体的表面积. 棱柱、棱锥、棱台都是由多个平面图形围成的多面体,它们的展开图是什么?如何计算它们的表面积?知识探究棱柱的侧面展开图是什么?如何计算它的表面积?h棱柱的侧面展开图正棱柱的侧面展开图 将空间图形问题转化为平面图形问题,是解立体几何问题最基本、最常用的方法.特别提醒 棱锥的侧面展开图是什么?如何计算它的表面积?侧面展开正棱锥的侧面展开图棱锥的侧面展开图棱台的侧面展开图是什么?如何计算它的表面积?棱台的侧面展开图侧面展开正棱台的侧面展开图棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它们的各个侧面面积与底面面积之和.例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.分析:四面体的展开图是由四个全等的等边三角形组成.因为BC=a,所以因此,四面体S-ABC 的表面积为交BC于点D.【解析】先求△SBC的面积,过点S作知识应用圆柱的表面积圆柱的侧面展开图是一个矩形,圆锥的表面积圆锥的侧面展开图是一个扇形,S圆台的表面积 参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么?圆台的侧面展开图是一个扇环,圆柱、圆锥、圆台三者的表面积公式之间有什么关系?【提升总结】知识应用
例2 如图,一个圆台形花盆盆口直径为20 cm,盆底直径为15 cm,底部渗水圆孔直径为1.5 cm,盆壁长15 cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100 毫升油漆,涂100个这样的花盆需要多少油漆(π取3.14,结果精确到1 毫升,可用计算器)?分析:只要求出每一个花盆外壁的表面积,就可求出油漆的用量.而花盆外壁的表面积等于花盆的侧面面积加上底面面积,再减去底面圆孔的面积.涂100个花盆需油漆:
0.1×100×100=1000(毫升).
答:涂100个这样的花盆约需要1000毫升油漆.【解析】如图,由圆台的表面积公式得一个花盆外壁的表面积 以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式.它们的体积公式可以统一为(S为底面面积,h为高).柱体体积一般柱体的体积也是其中S为底面面积,h为柱体的高.圆锥的体积公式是(其中S为底面面积,h为高),它的体积是同底等高的圆柱的体积的 .圆锥体积探究棱锥与同底等高的棱柱体积之间的关系.棱锥体积三棱锥与同底等高的三棱柱的关系等底等高的三棱锥体积相等.(其中S为底面面积,h为高). 由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是底面面积乘高的 . 经过探究得知,棱锥也是同底等高的棱柱体积
的 ,即棱锥的体积台体体积由于圆台(棱台)是由圆锥(棱锥)截成的,因此可以利用两个锥体的体积差,得到圆台(棱台)的体积公式(过程略)根据台体的特征,如何求台体的体积?棱台(圆台)的体积公式 其中 , 分别为上、下底面面积,h为棱台(圆台)的高. 分别为上、下底面面积,h 为台体高S为底面面积,
h为锥体高S为底面面积,
h为柱体高柱体、锥体、台体的体积公式之间有什么关系?公式有它的统一性.【提升总结】例3 有一堆规格相同的铁制(铁的密度是7.8 g/cm3)六角螺帽共重5.8 kg,已知底面是正六边形,边长为12 mm,内孔直径为10 mm,高为10 mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?知识应用【解析】六角螺帽的体积是六棱柱体积与圆柱体积的差,即所以螺帽的个数为5.8×1000÷(7.8×2.956)≈
252(个).答:这堆螺帽大约有252个.1.一个棱锥的三视图如图,则该棱锥的表面积为( )A.48+ B.48+
C.36+ D.36+A【解析】选A.由三视图得棱锥如图所示,
AO⊥底面BCD,O是BD的中点,BC=CD=6,
BC⊥CD,AO=4,AB=AD.
S△BCD= ×6×6=18,
S△ABD= ×6 ×4=12 .
取BC的中点E,连接AE,OE.
可得BC⊥AE,AE=
所以S△ABC=S△ACD= ×6×5=15,
所以S全=18+12 +15+15=48+12 .2.(2012·新课标全国卷)如图所示:
网格纸上小正方形的边长为1,
粗线画出的是某几何体的三视
图,则此几何体的体积为( )
A.6 B.9
C.12 D.18
【解析】选B.由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S= , BD5.(2012·上海高考)若一个圆锥的侧面展开图是面积
为2?的半圆面,则该圆锥的体积为_________ .
柱体、锥体、台体的表面积 圆台 圆柱 圆锥转化的思想柱体、锥体、台体的体积锥体台体柱体联系的观点 不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
