4.2.1 等差数列的概念(第三课时) 课件(共23张PPT)
文档属性
| 名称 | 4.2.1 等差数列的概念(第三课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 368.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 15:45:25 | ||
图片预览





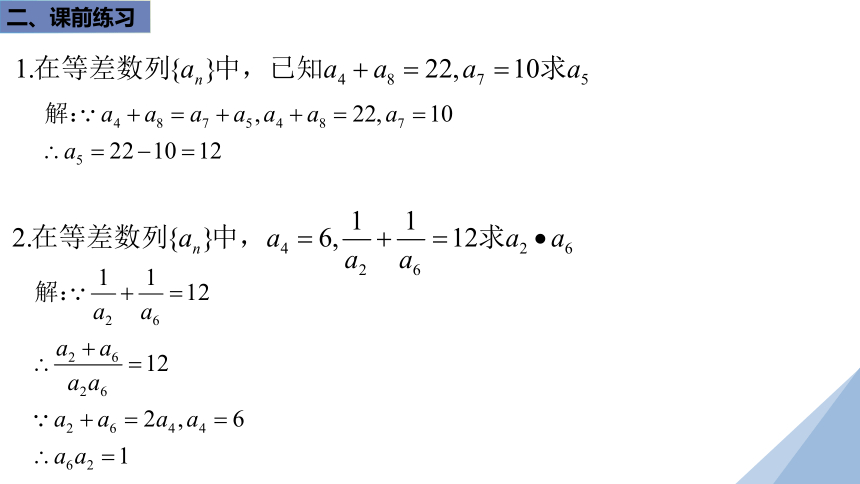



文档简介
(共23张PPT)
4.2.1 等差数列的概念
(第三课时)
教学目标:目录
1
2
掌握等差数列的性质及其应用
掌握等差数列的判断与证明方法
教学重点、难点:目录
等差数列性质及其应用
等差数列证明及其判断方法
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的。
等差中项:
等差数通项公式:
一、知识回顾
等差数列与一次函数关系:
等差性质:
公差d≠0的等差数列{an}的图象是点(n,an)组成的集合,这些点均匀分布在直线 上.
f(x)=dx+(a1-d)
一、知识回顾
二、课前练习
目录
CONTENTS
三、合作探究(一)
目录
CONTENTS
三、合作探究(一)
目录
CONTENTS
三、合作探究(二)
目录
CONTENTS
三、合作探究(二)
目录
CONTENTS
三、合作探究(二)
目录
三、合作探究
等差数列的判定方法:
定义法:
等差中项法:2
通项公式法:
目录
四、例题讲解
目录
四、例题讲解
目录
四、例题讲解
目录
四、例题讲解
五、课堂练习
五、课堂练习
五、课堂练习
目录
等差数列的判定方法:
定义法:
等差中项法:2
通项公式法:
六、课堂小结
七、作业
1.南宋数学家杨辉为我国古代数学研究作出了杰出贡献,他的著名研究成果“杨辉三角”记录于其重要著作《详解九章算法》,该著作中的“垛积术”问题介绍了高阶等差数列.以高阶等差数列中的二阶等差数列为例,其特点是从数列中的第二项开始,每一项与前一项的差构成等差数列.若某个二阶等差数列的前4项为:2,3,6,11,求该数列的第10项
七、作业
THANKS
4.2.1 等差数列的概念
(第三课时)
教学目标:目录
1
2
掌握等差数列的性质及其应用
掌握等差数列的判断与证明方法
教学重点、难点:目录
等差数列性质及其应用
等差数列证明及其判断方法
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的。
等差中项:
等差数通项公式:
一、知识回顾
等差数列与一次函数关系:
等差性质:
公差d≠0的等差数列{an}的图象是点(n,an)组成的集合,这些点均匀分布在直线 上.
f(x)=dx+(a1-d)
一、知识回顾
二、课前练习
目录
CONTENTS
三、合作探究(一)
目录
CONTENTS
三、合作探究(一)
目录
CONTENTS
三、合作探究(二)
目录
CONTENTS
三、合作探究(二)
目录
CONTENTS
三、合作探究(二)
目录
三、合作探究
等差数列的判定方法:
定义法:
等差中项法:2
通项公式法:
目录
四、例题讲解
目录
四、例题讲解
目录
四、例题讲解
目录
四、例题讲解
五、课堂练习
五、课堂练习
五、课堂练习
目录
等差数列的判定方法:
定义法:
等差中项法:2
通项公式法:
六、课堂小结
七、作业
1.南宋数学家杨辉为我国古代数学研究作出了杰出贡献,他的著名研究成果“杨辉三角”记录于其重要著作《详解九章算法》,该著作中的“垛积术”问题介绍了高阶等差数列.以高阶等差数列中的二阶等差数列为例,其特点是从数列中的第二项开始,每一项与前一项的差构成等差数列.若某个二阶等差数列的前4项为:2,3,6,11,求该数列的第10项
七、作业
THANKS
