第二章 代数式 复习课课件(共21张PPT)湘教版七年级数学上册
文档属性
| 名称 | 第二章 代数式 复习课课件(共21张PPT)湘教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 895.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 17:25:04 | ||
图片预览








文档简介
(共21张PPT)
第二章 代数式
第二章 复习课
1.会区分单项式和多项式.
2.能根据题目要求列出代数式,能说出所给代数式的意义.
3.会找同类项,会合并同类项.
4.知道去括号法则,能利用去括号法则及合并同类项进行整式的加减运算.
◎重点:单项式、多项式、同类项的概念及整式的加减.
◎难点:整式的化简、求值及应用.
1858年,苏格兰古董收藏家兰德在非洲的尼罗河边买进了一卷古埃及的纸草卷.他惊奇地发现,这个公元前1600年左右遗留下来的纸草卷中有一些明显的证据,表明古埃及人早在公元前1700年就已经在处理一些代数问题.从古埃及“法老”即国王统治的时期开始,人们一直在寻求这样一个相同的数学目标:使一个含有未知数的数学问题能够得到解决.这个纸草卷中就有一些含有未知数的数学问题,当然都是用象形文字表示的.例如,有一个问题翻译成数学语言为:“啊哈,它的全部,它的七分之一,其和等于19.”
这里的“啊哈”就是当时古埃及人的未知数,可以用字母来表示.代数对于算术来说是一个巨大的进步.
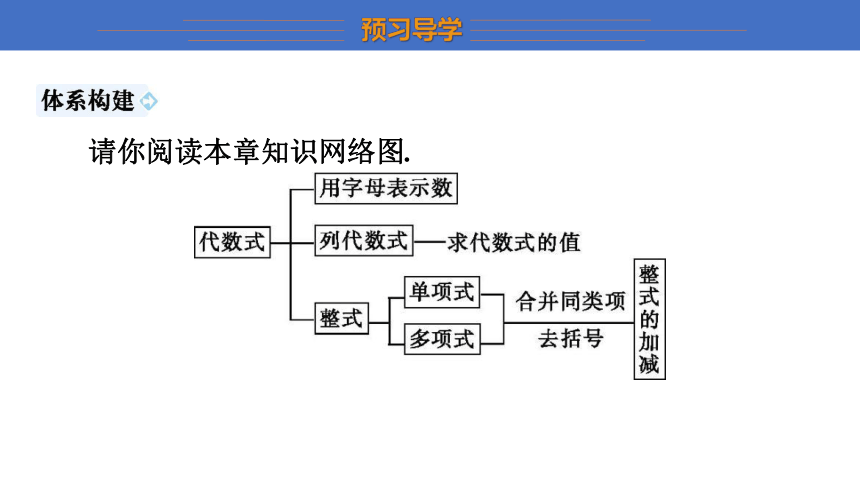
请你阅读本章知识网络图.
1.由 数 与 字母 的积组成的代数式叫做单项式,单独一个 字母 或一个 数 也是单项式.单项式中,与 字母相乘 的数叫做单项式的系数.所有 字母 的指数的 和 叫做这个单项式的次数.
数
字母
字母
数
字母相
乘
字母
和
2.由几个单项式的 和 组成的代数式叫做多项式,组成多项式的每个 单项式 叫做多项式的项,其中不含 字母 的项叫做常数项.多项式中 次数最高 的项的次数,叫做这个多项式的次数.
3.所含 字母 相同,并且 相同 字母的指数也分别 相同 的项叫做同类项.合并同类项时,只要把它们的系数 相加 ,字母和字母的指数 不变 .
和
单项式
字母
次数最高
字母
相同
相
同
相
加
不变
4.括号前是“+”,运用加法结合律把括号去掉,原括号里的各项的符号都 不变 .括号前是“-”号,把括号和它前面的“-”去掉,原括号里各项的符号都要 改变 .
5.整式加减的一般步骤是,先 去括号 ,再 合并同类项 .
不变
改变
去括号
合并同类
项
·导学建议·
教师可让学生自主回忆本章所学知识,之后同桌交流,最后学生总结本章知识网络图与核心梳理.学生在交流、讨论时,教师可参与到同学们中间去,和同学们以朋友的身份交流.
列代数式
1.某工厂一月份加工的产品为a件,二月份加工的产品数比一月份的3倍少5件,则二月份加工的产品为 (3a-5) 件.
(3a-5)
方法归纳交流 列代数式的关键在于:(1)正确分析 数量 关系,注意各个运算之间的顺序,并正确地使用括号;(2)把实际问题中的数量关系抽象为和、差、倍、分的关系.
数量
2.在代数式a,π,ab,a-b,,x2+x+1,5,2a,中,整式有 8 个;多项式有 3 个,单项式有 5 个,次数为2的单项式是 ab ,系数为1的单项式是 a .
8
3
5
ab
a
整式的有关概念
3.若a2bm与-0.8anb4相加后的结果仍是单项式,则n= 2 ,m= 4 .
4.合并同类项:(1)-a-a-2a= -4a ;
(2)-xy-5xy+6yx= 0 ;
(3)0.8ab2-ab2+0.2ab2= 0 .
2
4
-4a
0
0
同类项及合并同类项
方法归纳交流 同类项共同特征是含有的字母相同,相同字母的 指数 相同,与字母的先后顺序 无关 .
指数
无关
去括号法则
5.化简3x-2(x-3y)的结果是 x+6y .
6.把x2-8x+32y-4xy写成两式之差,其中一式不含y,一式含有y,将后一式作为减式.
解:原式=(x2-8x)-(-32y+4xy).
x+6y
·导学建议·
上述几个专题的题目都比较简单,可以让学生自己完成,教师通过提问的方式进行检查,对有疑难的地方进行解答.第6题学生可能会出现作为减式的放到括号内没有变号,可以让学生利用去括号法则进行检查,再写出正确结果.教师可补充说明:当多项式中含有大、中、小括号时,通常先去掉小括号,再去掉中括号,最后去掉大括号,也可让学生根据题目特点灵活选择方法.
整式的加减
7.(1)先化简再求值:(2x2y-4xy2)-,其中x=-1,y=2.
(2)已知x2+3x+5的值为7,求代数式3x2+9x-2的值.
解:(1)原式=2x2y-4xy2-xy2-x2y=x2y-xy2.
当x=-1,y=2时,原式=x2y-xy2=20.
(2)因为x2+3x+5的值为7,即x2+3x=2,所以3x2+9x-2=3(x2+3x)-2=3×2-2=4.
方法归纳交流 求代数式的值的方法主要有两种:一种是直接代入法;另一种是 整体 代入法.两种方法的选择主要取决于给出的条件.
整体
8.公交车从站点出发时车上有(6a-2b)人,经过下一个站点时下了一半人,但又上车若干人,这时车上有(10a-3b)人,问中途上车多少人?
解:(10a-3b)-(6a-2b)=10a-3b-3a+b=7a-2b.
答:中途上车(7a-2b)人.
整式加减的应用
方法归纳交流 解决与实际生活有关的问题时,要先根据题目条件列出 代数式 ,再利用整式的加减求出结果.
代数式
·导学建议·
要通过合作探究让学生多归纳总结,培养学生的归纳总结能力.第6题可以利用去括号法则逆向思维进行考虑,第7题(2)要注意整体代入.
第二章 代数式
第二章 复习课
1.会区分单项式和多项式.
2.能根据题目要求列出代数式,能说出所给代数式的意义.
3.会找同类项,会合并同类项.
4.知道去括号法则,能利用去括号法则及合并同类项进行整式的加减运算.
◎重点:单项式、多项式、同类项的概念及整式的加减.
◎难点:整式的化简、求值及应用.
1858年,苏格兰古董收藏家兰德在非洲的尼罗河边买进了一卷古埃及的纸草卷.他惊奇地发现,这个公元前1600年左右遗留下来的纸草卷中有一些明显的证据,表明古埃及人早在公元前1700年就已经在处理一些代数问题.从古埃及“法老”即国王统治的时期开始,人们一直在寻求这样一个相同的数学目标:使一个含有未知数的数学问题能够得到解决.这个纸草卷中就有一些含有未知数的数学问题,当然都是用象形文字表示的.例如,有一个问题翻译成数学语言为:“啊哈,它的全部,它的七分之一,其和等于19.”
这里的“啊哈”就是当时古埃及人的未知数,可以用字母来表示.代数对于算术来说是一个巨大的进步.
请你阅读本章知识网络图.
1.由 数 与 字母 的积组成的代数式叫做单项式,单独一个 字母 或一个 数 也是单项式.单项式中,与 字母相乘 的数叫做单项式的系数.所有 字母 的指数的 和 叫做这个单项式的次数.
数
字母
字母
数
字母相
乘
字母
和
2.由几个单项式的 和 组成的代数式叫做多项式,组成多项式的每个 单项式 叫做多项式的项,其中不含 字母 的项叫做常数项.多项式中 次数最高 的项的次数,叫做这个多项式的次数.
3.所含 字母 相同,并且 相同 字母的指数也分别 相同 的项叫做同类项.合并同类项时,只要把它们的系数 相加 ,字母和字母的指数 不变 .
和
单项式
字母
次数最高
字母
相同
相
同
相
加
不变
4.括号前是“+”,运用加法结合律把括号去掉,原括号里的各项的符号都 不变 .括号前是“-”号,把括号和它前面的“-”去掉,原括号里各项的符号都要 改变 .
5.整式加减的一般步骤是,先 去括号 ,再 合并同类项 .
不变
改变
去括号
合并同类
项
·导学建议·
教师可让学生自主回忆本章所学知识,之后同桌交流,最后学生总结本章知识网络图与核心梳理.学生在交流、讨论时,教师可参与到同学们中间去,和同学们以朋友的身份交流.
列代数式
1.某工厂一月份加工的产品为a件,二月份加工的产品数比一月份的3倍少5件,则二月份加工的产品为 (3a-5) 件.
(3a-5)
方法归纳交流 列代数式的关键在于:(1)正确分析 数量 关系,注意各个运算之间的顺序,并正确地使用括号;(2)把实际问题中的数量关系抽象为和、差、倍、分的关系.
数量
2.在代数式a,π,ab,a-b,,x2+x+1,5,2a,中,整式有 8 个;多项式有 3 个,单项式有 5 个,次数为2的单项式是 ab ,系数为1的单项式是 a .
8
3
5
ab
a
整式的有关概念
3.若a2bm与-0.8anb4相加后的结果仍是单项式,则n= 2 ,m= 4 .
4.合并同类项:(1)-a-a-2a= -4a ;
(2)-xy-5xy+6yx= 0 ;
(3)0.8ab2-ab2+0.2ab2= 0 .
2
4
-4a
0
0
同类项及合并同类项
方法归纳交流 同类项共同特征是含有的字母相同,相同字母的 指数 相同,与字母的先后顺序 无关 .
指数
无关
去括号法则
5.化简3x-2(x-3y)的结果是 x+6y .
6.把x2-8x+32y-4xy写成两式之差,其中一式不含y,一式含有y,将后一式作为减式.
解:原式=(x2-8x)-(-32y+4xy).
x+6y
·导学建议·
上述几个专题的题目都比较简单,可以让学生自己完成,教师通过提问的方式进行检查,对有疑难的地方进行解答.第6题学生可能会出现作为减式的放到括号内没有变号,可以让学生利用去括号法则进行检查,再写出正确结果.教师可补充说明:当多项式中含有大、中、小括号时,通常先去掉小括号,再去掉中括号,最后去掉大括号,也可让学生根据题目特点灵活选择方法.
整式的加减
7.(1)先化简再求值:(2x2y-4xy2)-,其中x=-1,y=2.
(2)已知x2+3x+5的值为7,求代数式3x2+9x-2的值.
解:(1)原式=2x2y-4xy2-xy2-x2y=x2y-xy2.
当x=-1,y=2时,原式=x2y-xy2=20.
(2)因为x2+3x+5的值为7,即x2+3x=2,所以3x2+9x-2=3(x2+3x)-2=3×2-2=4.
方法归纳交流 求代数式的值的方法主要有两种:一种是直接代入法;另一种是 整体 代入法.两种方法的选择主要取决于给出的条件.
整体
8.公交车从站点出发时车上有(6a-2b)人,经过下一个站点时下了一半人,但又上车若干人,这时车上有(10a-3b)人,问中途上车多少人?
解:(10a-3b)-(6a-2b)=10a-3b-3a+b=7a-2b.
答:中途上车(7a-2b)人.
整式加减的应用
方法归纳交流 解决与实际生活有关的问题时,要先根据题目条件列出 代数式 ,再利用整式的加减求出结果.
代数式
·导学建议·
要通过合作探究让学生多归纳总结,培养学生的归纳总结能力.第6题可以利用去括号法则逆向思维进行考虑,第7题(2)要注意整体代入.
同课章节目录
