27.1.3 圆周角 课件(共19张PPT) 华东师大版九年级下册
文档属性
| 名称 | 27.1.3 圆周角 课件(共19张PPT) 华东师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 17:35:53 | ||
图片预览


文档简介
(共19张PPT)
第27章 圆
27.1.3 圆周角
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
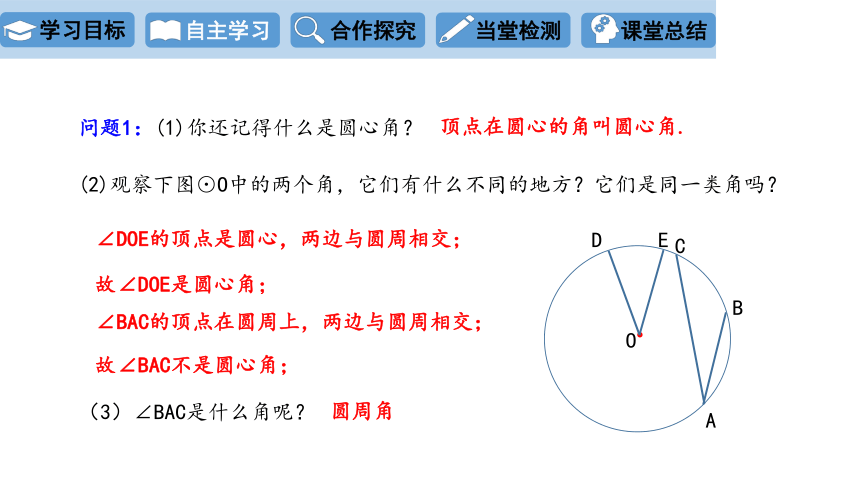
问题1:(1)你还记得什么是圆心角?
顶点在圆心的角叫圆心角.
(2)观察下图⊙O中的两个角,它们有什么不同的地方?它们是同一类角吗?
O
D
E
C
A
B
∠DOE的顶点是圆心,两边与圆周相交;
(3)∠BAC是什么角呢?
∠BAC的顶点在圆周上,两边与圆周相交;
故∠DOE是圆心角;
故∠BAC不是圆心角;
圆周角
合作探究
当堂检测
学习目标
课堂总结
自主学习
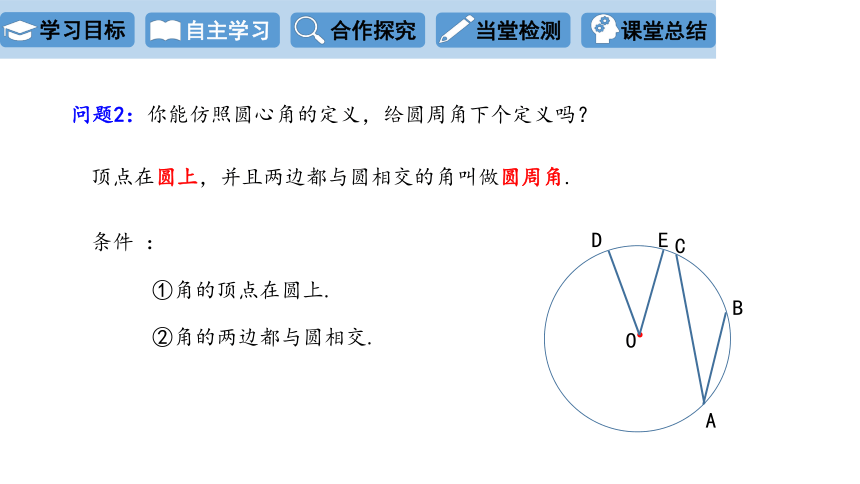
问题2:你能仿照圆心角的定义,给圆周角下个定义吗?
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
条件 :
①角的顶点在圆上.
②角的两边都与圆相交.
O
D
E
C
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
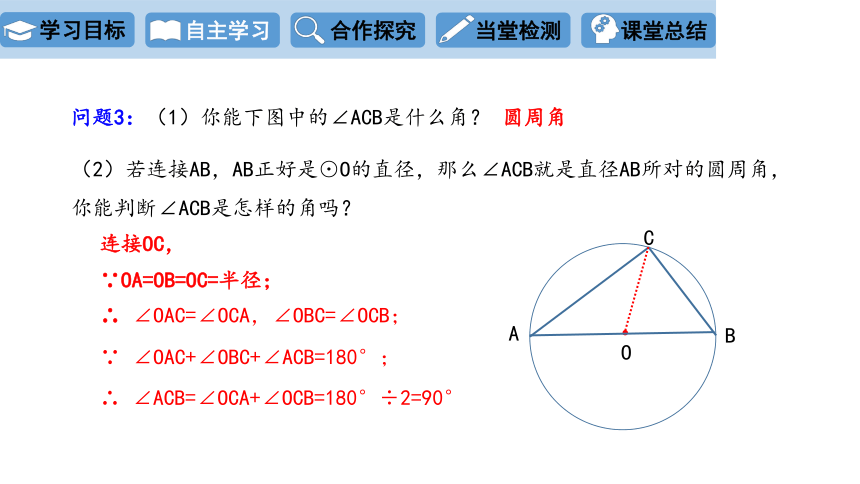
问题3:(1)你能下图中的∠ACB是什么角?
O
A
C
B
圆周角
(2)若连接AB,AB正好是⊙O的直径,那么∠ACB就是直径AB所对的圆周角,你能判断∠ACB是怎样的角吗?
连接OC,
∵OA=OB=OC=半径;
∴ ∠OAC=∠OCA,∠OBC=∠OCB;
∵ ∠OAC+∠OBC+∠ACB=180°;
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°
合作探究
当堂检测
学习目标
课堂总结
自主学习
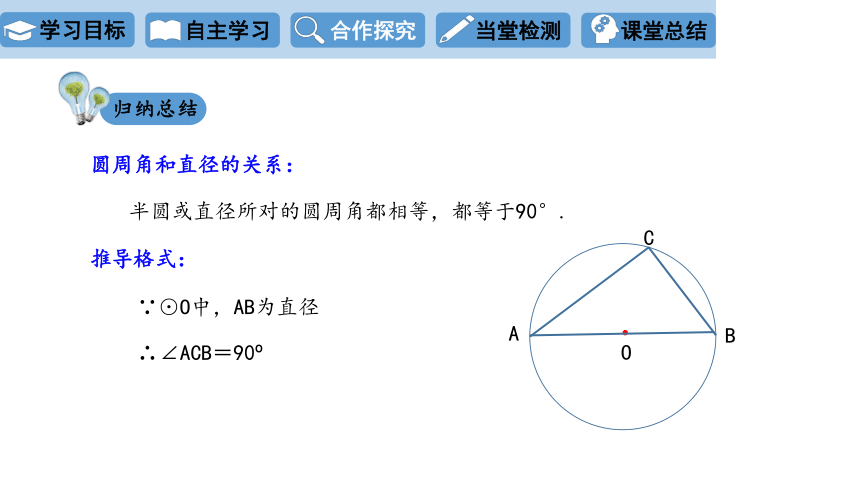
圆周角和直径的关系:
归纳总结
半圆或直径所对的圆周角都相等,都等于90°.
O
A
C
B
推导格式:
∵⊙O中,AB为直径
∴∠ACB=90
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:圆周角定理
问题:(1)一条弧所对的圆心角有多少个?圆周角有多少个
由于顶点不确定,同一条弧所对的圆周角有无数个.
同一个圆中,同一条弧所对的圆心角只有一个;
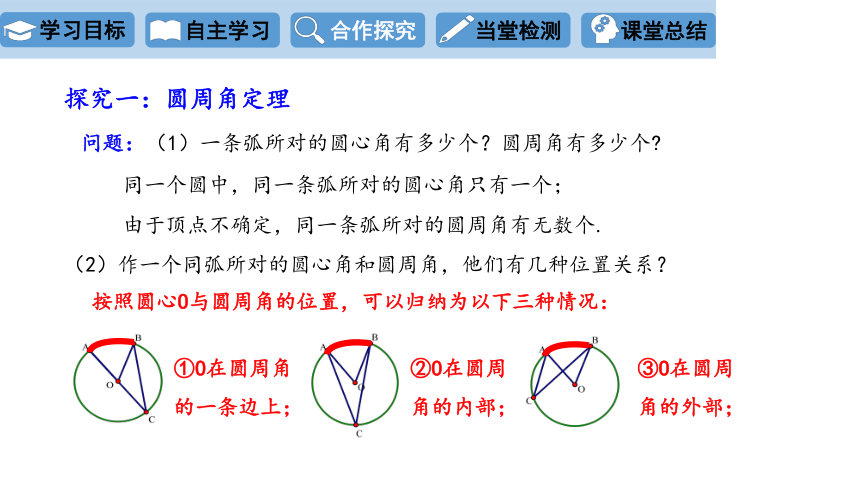
(2)作一个同弧所对的圆心角和圆周角,他们有几种位置关系?
按照圆心O与圆周角的位置,可以归纳为以下三种情况:
①O在圆周角的一条边上;
②O在圆周角的内部;
③O在圆周角的外部;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)同弧所对的圆心角和圆周角有什么数量关系吗?数量关系受位置关系的影响吗?
①O在圆周角的一条边上:
根据三种位置关系分别分析圆心角和圆周角的数量关系.
∵∠AOB是△BCO的外角,
∵OB=OC,
∴∠B=∠C.
∴∠AOB=2∠C.
∴∠AOB=∠C+∠B.
合作探究
当堂检测
学习目标
课堂总结
自主学习
②O在圆周角的内部:
作直径CD.利用①的结论,得
∴∠A0B =∠AOD+∠BOD=2(∠ACD+∠BCD)=2∠ACB.
∠AOD=2∠ACD,∠BOD=2∠BCD,
③O在圆周角的外部:
作直径CD.利用①的结论,得
D
D
∴∠AOB =∠AOD-∠BOD=2(∠ACD-∠BCD)=2∠ACB.
∠AOD=2∠ACD,∠BOD=2∠BCD,
同弧所对的圆心角的度数=2×圆周角的度数,不受位置关系的影响.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆周角定理:
归纳总结
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.相等的圆周角所对的弧相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
(1)∠BOC= ,
理由是 ;
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(2)∠BDC= ,理由是 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:圆周角定理的推论
问题1:圆周角和直径的关系:半圆或直径所对的圆周角都相等,都等于90°.如果把条件和结论反过来,还能成立吗?即圆周角是 90 (直角)所对的弦是直径吗?
∴90°圆周角∠ACB所对的圆心角∠AOB=180°,
∵一条弧所对的圆周角等于它所对圆心角的一半,
∴A,O,B三点在同一直线上,
O
A
C
B
故弦AB为圆的直径.
推论1:90°的圆周角所对的弦是直径.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如果在☉O内任意画一个多边形,多边形的各个顶点在圆周上,这个圆和这个多边形有什么关系呢?
如果一个圆经过一个多边形的各个顶点,
O
B
E
A
C
这个圆就叫做这个多边形的外接圆;
D
这个多边形就叫做这个圆的内接多边形;
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图所示,分别连接OB、OD.
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
猜想:∠A+∠C=180 ,∠B+∠D=180 .
同理∠B+∠D=180°,
O
B
D
A
C
问题3:如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆. 四边形的四个角有什么关系呢?你能证明吗?
推论2:圆内接四边形的对角互补.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设∠A,∠B,∠C的度数分别对于2x,3x,6x,
4.在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.
求这个四边形各角的度数.
∵四边形ABCD内接于圆,
∴∠A+∠C=∠B+∠D=180°,
∵2x+6x=180°,
∴ x=22.5°.
∴∠A=45°,∠B=67.5°,∠C =135°,
∴∠D=180°-67.5°=112.5°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆周角和直径的关系:
半圆或直径所对的圆周角都相等,都等于90°.
圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.相等的圆周角所对的弧相等.
圆周角定理的推论:
推论2:圆内接四边形的对角互补.
推论1:90°的圆周角所对的弦是直径.
第27章 圆
27.1.3 圆周角
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题1:(1)你还记得什么是圆心角?
顶点在圆心的角叫圆心角.
(2)观察下图⊙O中的两个角,它们有什么不同的地方?它们是同一类角吗?
O
D
E
C
A
B
∠DOE的顶点是圆心,两边与圆周相交;
(3)∠BAC是什么角呢?
∠BAC的顶点在圆周上,两边与圆周相交;
故∠DOE是圆心角;
故∠BAC不是圆心角;
圆周角
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:你能仿照圆心角的定义,给圆周角下个定义吗?
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
条件 :
①角的顶点在圆上.
②角的两边都与圆相交.
O
D
E
C
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题3:(1)你能下图中的∠ACB是什么角?
O
A
C
B
圆周角
(2)若连接AB,AB正好是⊙O的直径,那么∠ACB就是直径AB所对的圆周角,你能判断∠ACB是怎样的角吗?
连接OC,
∵OA=OB=OC=半径;
∴ ∠OAC=∠OCA,∠OBC=∠OCB;
∵ ∠OAC+∠OBC+∠ACB=180°;
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆周角和直径的关系:
归纳总结
半圆或直径所对的圆周角都相等,都等于90°.
O
A
C
B
推导格式:
∵⊙O中,AB为直径
∴∠ACB=90
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:圆周角定理
问题:(1)一条弧所对的圆心角有多少个?圆周角有多少个
由于顶点不确定,同一条弧所对的圆周角有无数个.
同一个圆中,同一条弧所对的圆心角只有一个;
(2)作一个同弧所对的圆心角和圆周角,他们有几种位置关系?
按照圆心O与圆周角的位置,可以归纳为以下三种情况:
①O在圆周角的一条边上;
②O在圆周角的内部;
③O在圆周角的外部;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)同弧所对的圆心角和圆周角有什么数量关系吗?数量关系受位置关系的影响吗?
①O在圆周角的一条边上:
根据三种位置关系分别分析圆心角和圆周角的数量关系.
∵∠AOB是△BCO的外角,
∵OB=OC,
∴∠B=∠C.
∴∠AOB=2∠C.
∴∠AOB=∠C+∠B.
合作探究
当堂检测
学习目标
课堂总结
自主学习
②O在圆周角的内部:
作直径CD.利用①的结论,得
∴∠A0B =∠AOD+∠BOD=2(∠ACD+∠BCD)=2∠ACB.
∠AOD=2∠ACD,∠BOD=2∠BCD,
③O在圆周角的外部:
作直径CD.利用①的结论,得
D
D
∴∠AOB =∠AOD-∠BOD=2(∠ACD-∠BCD)=2∠ACB.
∠AOD=2∠ACD,∠BOD=2∠BCD,
同弧所对的圆心角的度数=2×圆周角的度数,不受位置关系的影响.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆周角定理:
归纳总结
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.相等的圆周角所对的弧相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
(1)∠BOC= ,
理由是 ;
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(2)∠BDC= ,理由是 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:圆周角定理的推论
问题1:圆周角和直径的关系:半圆或直径所对的圆周角都相等,都等于90°.如果把条件和结论反过来,还能成立吗?即圆周角是 90 (直角)所对的弦是直径吗?
∴90°圆周角∠ACB所对的圆心角∠AOB=180°,
∵一条弧所对的圆周角等于它所对圆心角的一半,
∴A,O,B三点在同一直线上,
O
A
C
B
故弦AB为圆的直径.
推论1:90°的圆周角所对的弦是直径.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如果在☉O内任意画一个多边形,多边形的各个顶点在圆周上,这个圆和这个多边形有什么关系呢?
如果一个圆经过一个多边形的各个顶点,
O
B
E
A
C
这个圆就叫做这个多边形的外接圆;
D
这个多边形就叫做这个圆的内接多边形;
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图所示,分别连接OB、OD.
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
猜想:∠A+∠C=180 ,∠B+∠D=180 .
同理∠B+∠D=180°,
O
B
D
A
C
问题3:如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆. 四边形的四个角有什么关系呢?你能证明吗?
推论2:圆内接四边形的对角互补.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:设∠A,∠B,∠C的度数分别对于2x,3x,6x,
4.在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.
求这个四边形各角的度数.
∵四边形ABCD内接于圆,
∴∠A+∠C=∠B+∠D=180°,
∵2x+6x=180°,
∴ x=22.5°.
∴∠A=45°,∠B=67.5°,∠C =135°,
∴∠D=180°-67.5°=112.5°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆周角和直径的关系:
半圆或直径所对的圆周角都相等,都等于90°.
圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.相等的圆周角所对的弧相等.
圆周角定理的推论:
推论2:圆内接四边形的对角互补.
推论1:90°的圆周角所对的弦是直径.
