27.1.2 圆的对称性 第2课时 课件(共16张PPT) 华东师大版九年级下册数学
文档属性
| 名称 | 27.1.2 圆的对称性 第2课时 课件(共16张PPT) 华东师大版九年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
第27章 圆
27.1.2 圆的对称性
第2课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
2.灵活运用垂径定理解决有关圆的问题.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
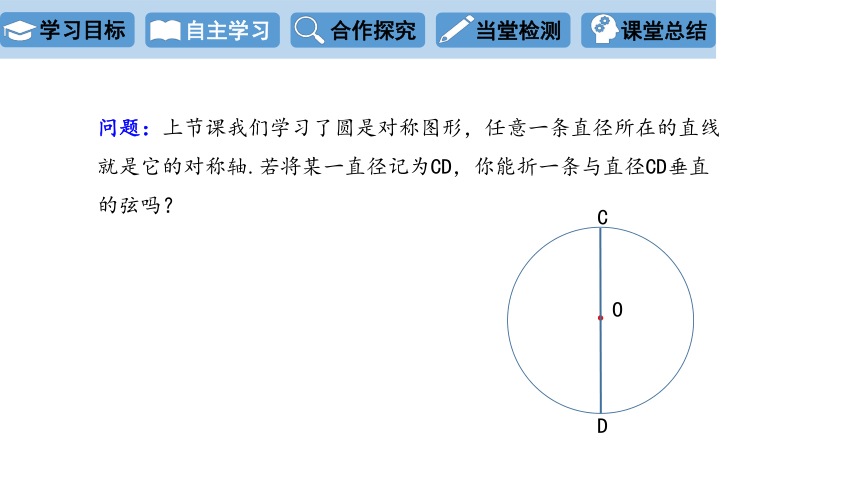
问题:上节课我们学习了圆是对称图形,任意一条直径所在的直线就是它的对称轴.若将某一直径记为CD,你能折一条与直径CD垂直的弦吗?
O
C
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:垂径定理
问题提出:若将弦记为AB,将垂足记为M,则有 AB⊥CD于M,你能发现图中有哪些等量关系?
(1)如何证明两条边相等?
在边长长度未知的情况下,证明分别包含两条边的两个三角形全等.
猜想:AM=BM.
O
C
D
A
B
M└
问题探究:
(2)AM、BM分别在哪两个三角形内?
构建三角形,分别连接AO、BO.得到△AOM、△BOM.
合作探究
当堂检测
学习目标
课堂总结
自主学习
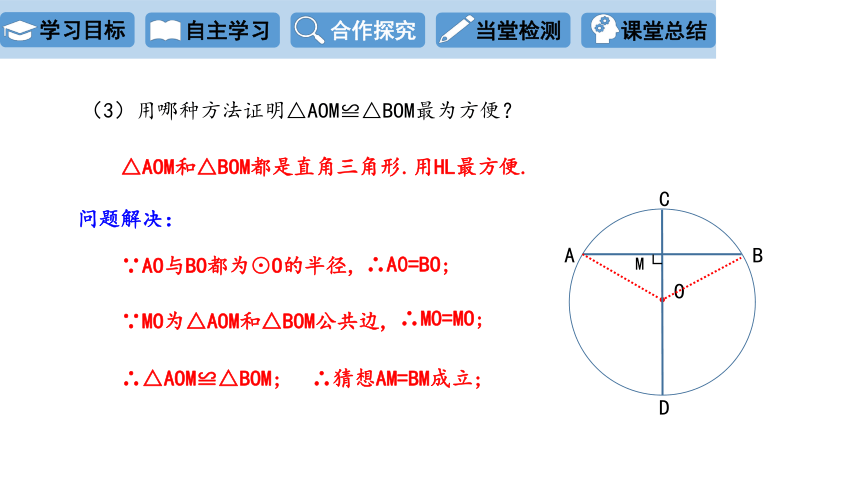
(3)用哪种方法证明△AOM≌△BOM最为方便?
△AOM和△BOM都是直角三角形.用HL最方便.
O
C
D
A
B
M└
∴A0=BO;
∴MO=MO;
∵AO与BO都为⊙O的半径,
∵MO为△AOM和△BOM公共边,
问题解决:
∴△AOM≌△BOM;
∴猜想AM=BM成立;
合作探究
当堂检测
学习目标
课堂总结
自主学习
提示:根据在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
∠AOC=∠BOC;
注意:任意一条直径都是圆的对称轴,得到两个半圆.
思考:已知AM=BM,你还能推出图中其他等量关系吗?
O
C
D
A
B
M└
︵
AC=CB,
︵
︵
∵CD=DC,
︵
︵
∴AD=DB,
︵
︵
AC=CB,
︵
合作探究
当堂检测
学习目标
课堂总结
自主学习
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理:
推导格式:
归纳总结
∵ CD是直径,CD⊥AB,
∴ AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
O
C
D
A
B
M└
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
下列图形是否具备垂径定理的条件?
没有垂直
O
A
B
C
A
B
O
E
A
B
D
C
O
E
CD没有过圆心
×
√
×
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:垂径定理的推论
问题提出: 如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)转换为数学语言,得到下列条件:
① CD是直径 ;②CD⊥AB,垂足为M ;
③ AM=BM;④ ; ⑤ .
问题探究:
任何两个条件都可以推出其他三个结论吗?
猜想:已知条件①③,推出②④⑤.
O
C
D
A
B
M
⌒
⌒
AC =BC
⌒
⌒
AD =BD
合作探究
当堂检测
学习目标
课堂总结
自主学习
已知: CD是直径 ;AM=BM;
求证:CD⊥AB,垂足为M ; ;
(1)条件和结论之间有什么联系吗?
所有信息都是从垂径定理中衍生出来的,先证明CD⊥AB,然后借助垂径定理证明
O
C
D
A
B
M
⌒
⌒
AC =BC
⌒
⌒
AD =BD
⌒
⌒
AC =BC,
⌒
⌒
AD =BD
(2)有什么方法证明线段垂直?
可以借助全等,证明两条线段相交的角度为90°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
C
D
A
B
M
∴A0=BO;
∵AM=BM;
∵AO与BO都为⊙O的半径,
∴△AOB为等腰三角形,∠MAO=∠MBO
问题解决:
∴△AOM≌△BOM;
∴∠AMO=∠BMO;
构建三角形,分别连接AO、BO.得到△AOM、△BOM.
已知: CD是直径 ;AM=BM;
求证:CD⊥AB,垂足为M ; ;
⌒
⌒
AC =BC
⌒
⌒
AD =BD
∵∠AMO+∠BMO=180°,
∴∠AMO=∠BMO=90°;
∴CD⊥AB,
∴
⌒
⌒
AC =BC,
⌒
⌒
AD =BD;
合作探究
当堂检测
学习目标
课堂总结
自主学分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
垂径定理的推论:
归纳总结
平分弧的直径垂直平分这条弧所对的弦.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,AB是⊙0中的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BC
⌒
⌒
C
A
B
C
O
D
E
.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在半径为30㎜的⊙O中,弦AB=36㎜,则O到AB的距离是= ,∠OAB的余弦值= .
O
A
B
P
0.6
24mm
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
解:连接OA,
合作探究
当堂检测
学习目标
课堂总结
自主学习
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理:
平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
垂径定理的推论:
平分弧的直径垂直平分这条弧所对的弦.
第27章 圆
27.1.2 圆的对称性
第2课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
2.灵活运用垂径定理解决有关圆的问题.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题:上节课我们学习了圆是对称图形,任意一条直径所在的直线就是它的对称轴.若将某一直径记为CD,你能折一条与直径CD垂直的弦吗?
O
C
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:垂径定理
问题提出:若将弦记为AB,将垂足记为M,则有 AB⊥CD于M,你能发现图中有哪些等量关系?
(1)如何证明两条边相等?
在边长长度未知的情况下,证明分别包含两条边的两个三角形全等.
猜想:AM=BM.
O
C
D
A
B
M└
问题探究:
(2)AM、BM分别在哪两个三角形内?
构建三角形,分别连接AO、BO.得到△AOM、△BOM.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)用哪种方法证明△AOM≌△BOM最为方便?
△AOM和△BOM都是直角三角形.用HL最方便.
O
C
D
A
B
M└
∴A0=BO;
∴MO=MO;
∵AO与BO都为⊙O的半径,
∵MO为△AOM和△BOM公共边,
问题解决:
∴△AOM≌△BOM;
∴猜想AM=BM成立;
合作探究
当堂检测
学习目标
课堂总结
自主学习
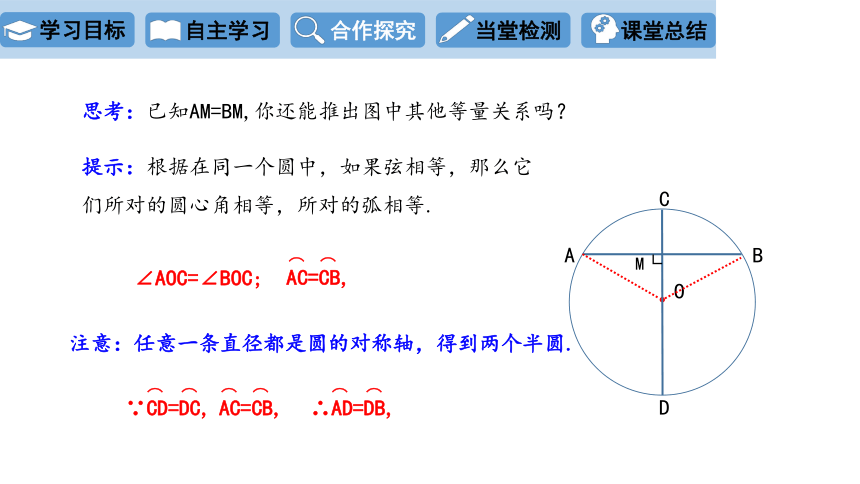
提示:根据在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
∠AOC=∠BOC;
注意:任意一条直径都是圆的对称轴,得到两个半圆.
思考:已知AM=BM,你还能推出图中其他等量关系吗?
O
C
D
A
B
M└
︵
AC=CB,
︵
︵
∵CD=DC,
︵
︵
∴AD=DB,
︵
︵
AC=CB,
︵
合作探究
当堂检测
学习目标
课堂总结
自主学习
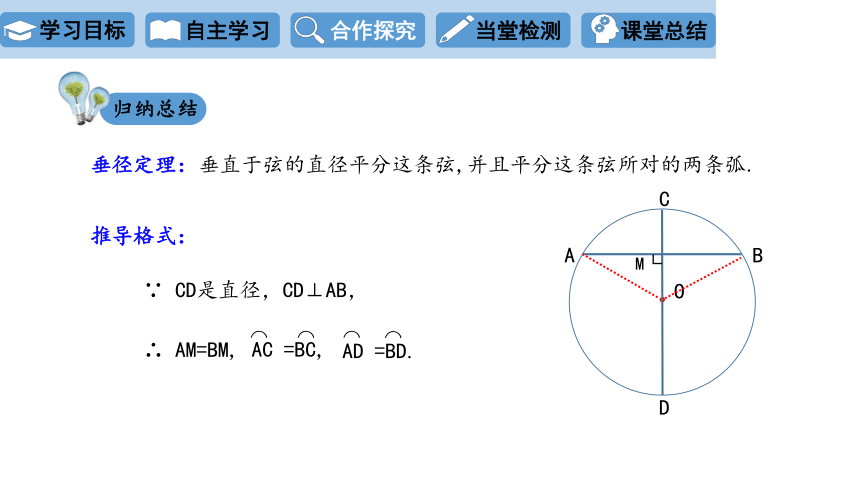
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理:
推导格式:
归纳总结
∵ CD是直径,CD⊥AB,
∴ AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
O
C
D
A
B
M└
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
下列图形是否具备垂径定理的条件?
没有垂直
O
A
B
C
A
B
O
E
A
B
D
C
O
E
CD没有过圆心
×
√
×
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:垂径定理的推论
问题提出: 如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)转换为数学语言,得到下列条件:
① CD是直径 ;②CD⊥AB,垂足为M ;
③ AM=BM;④ ; ⑤ .
问题探究:
任何两个条件都可以推出其他三个结论吗?
猜想:已知条件①③,推出②④⑤.
O
C
D
A
B
M
⌒
⌒
AC =BC
⌒
⌒
AD =BD
合作探究
当堂检测
学习目标
课堂总结
自主学习
已知: CD是直径 ;AM=BM;
求证:CD⊥AB,垂足为M ; ;
(1)条件和结论之间有什么联系吗?
所有信息都是从垂径定理中衍生出来的,先证明CD⊥AB,然后借助垂径定理证明
O
C
D
A
B
M
⌒
⌒
AC =BC
⌒
⌒
AD =BD
⌒
⌒
AC =BC,
⌒
⌒
AD =BD
(2)有什么方法证明线段垂直?
可以借助全等,证明两条线段相交的角度为90°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
C
D
A
B
M
∴A0=BO;
∵AM=BM;
∵AO与BO都为⊙O的半径,
∴△AOB为等腰三角形,∠MAO=∠MBO
问题解决:
∴△AOM≌△BOM;
∴∠AMO=∠BMO;
构建三角形,分别连接AO、BO.得到△AOM、△BOM.
已知: CD是直径 ;AM=BM;
求证:CD⊥AB,垂足为M ; ;
⌒
⌒
AC =BC
⌒
⌒
AD =BD
∵∠AMO+∠BMO=180°,
∴∠AMO=∠BMO=90°;
∴CD⊥AB,
∴
⌒
⌒
AC =BC,
⌒
⌒
AD =BD;
合作探究
当堂检测
学习目标
课堂总结
自主学分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
垂径定理的推论:
归纳总结
平分弧的直径垂直平分这条弧所对的弦.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,AB是⊙0中的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BC
⌒
⌒
C
A
B
C
O
D
E
.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在半径为30㎜的⊙O中,弦AB=36㎜,则O到AB的距离是= ,∠OAB的余弦值= .
O
A
B
P
0.6
24mm
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
解:连接OA,
合作探究
当堂检测
学习目标
课堂总结
自主学习
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理:
平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
垂径定理的推论:
平分弧的直径垂直平分这条弧所对的弦.
