27.2.1 点与圆的位置关系 课件(共18张PPT) 华东师大版九年级下册
文档属性
| 名称 | 27.2.1 点与圆的位置关系 课件(共18张PPT) 华东师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 496.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 17:39:08 | ||
图片预览






文档简介
(共18张PPT)
第27章 圆
27.2 与圆有关的位置关系
1. 点与圆的位置关系
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.知道点与圆的位置关系,能通过点与圆心的距离与半径的关系判断点与圆的位置关系,反之亦可.
2.知道不在同一直线上的三点确定一个圆,知道三角形的外心、圆的内接三角形等概念,会画三角形的外接圆.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
小玉和小兰设计了一种简易版的飞镖游戏,如下图所示,规则如下:射中红色部分记三分,白色部分记两分,黑色部分记一分,脱靶倒扣一分. 小玉和小兰进行了PK,一人两次机会,黄色飞镖是 小玉射的,红色飞镖是小兰射的,你能分出谁胜谁负吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
规则:射中红色部分记三分,白色部分记两分,黑色部分记一分,脱靶倒扣一分.
小玉:
小兰:
射中红色部分+3,脱靶-1,共计两分;
射中白色部分+2,黑色部分+1,共计三分;
小兰以一分优势获得胜利.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:点和圆的位置关系
问题1:(1)飞镖所在位置有几种可能性呢?
(2)如果把靶子看成是一个圆形,飞镖游戏体现了什么位置关系?
①在圆内;
②在圆上;
③在圆外;
体现了平面内点与圆的位置关系.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)你能将上述三种位置关系转化为数学语言吗?
提示:圆是由所有与定点(圆心)的距离等于定长(半径)的点组成的平面图形.
点与圆心的距离小于半径;
①点P在圆内
②点P在圆上
③点P在圆外
点与圆心的距离等于半径;
点与圆心的距离大于半径;
合作探究
当堂检测
学习目标
课堂总结
自主学习
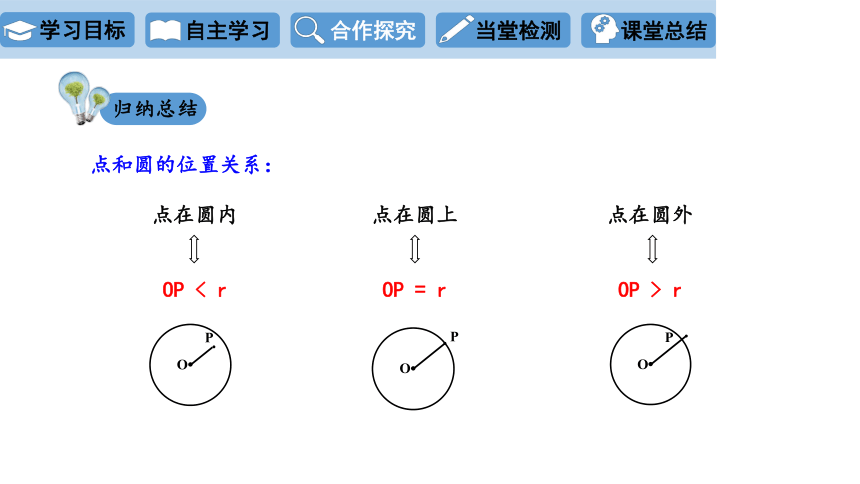
点和圆的位置关系:
归纳总结
点在圆内
OP < r
OP = r
OP > r
O
P
O
P
O
P
点在圆上
点在圆外
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:不在同一直线上的三点确定圆
问题1:(1)要画出一个确定的圆,需要具备什么条件呢?
(2)过已知点A,你能作出多少个圆呢?
一是圆心,二是半径.
∵圆心与半径都不能确定,
∴可作无数个圆.
·
·
·
·
A
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)过已知点A、B,你能作出多少个圆呢?
∵所作圆经过点A、B,
这些圆的圆心都在线段AB的垂直平分线上.
(4)这些圆的圆心分布有什么特点?
∴圆心O到A、B的距离是相等的
∴可作无数个圆.
·
·
·
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
(5)已知,不在同一条直线上三点A,B,C,过这三点能不能作圆,你能作多少个圆?
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
由于两条垂直平分线的交点只有一个,所以就只能确定一个圆心,也就只能作出一个圆.
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
D
E
G
F
●
O
不在同一条直线上的三个点确定一个圆.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图所示,现在有一个三角形ABC,你能画出这个三角形的外接圆吗?
O
N
M
F
E
A
B
C
1、作线段AB的垂直平分线MN;
2、作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
一个三角形的外接圆也是唯一的.
合作探究
当堂检测
学习目标
课堂总结
自主学习
⊙O叫做△ABC的外接圆;
△ABC叫做⊙O的内接三角形.
三角形外接圆的圆心叫做这个三角形的外心.
三角形的外心是三角形三条边的垂直平分线的交点.
O
A
B
C
归纳总结
三角形的外心到三角形三个顶点的距离相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
Q
P
M
R
A
B
C
A.点P B.点Q
C.点R D.点M
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知如图,矩形ABCD的边长AB=3,BC=4,若以B为圆心,以5为半径作圆,则点A、C、D三点中,在圆上的点是_____;在圆内的点是_______.若以B为圆心,以4为半径作圆,则A、C、D三点中,在圆内的点是_____;在圆上的点是______;在圆外的点是_______.
D
A、C
A
C
D
C
D
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知 Rt△ABC中 ,∠C=90°若 AC=12cm,BC=5cm,求的外接圆半径.
解:∵90°的圆周角所对的弦是直径,
故Rt△ABC 的外接圆半径为6.5cm.
∴AB=13cm,OA=6.5cm.
∵∠C=90°,AC=12cm,BC=5cm.
∴AB为圆O的直径,圆心0在AB的中点上,
合作探究
当堂检测
学习目标
课堂总结
自主学习
点和圆的位置关系:
①点P在圆内
②点P在圆上
③点P在圆外
OP < r
OP = r
OP > r
不在同一条直线上的三个点确定一个圆.
三角形外接圆的圆心叫做这个三角形的外心.
第27章 圆
27.2 与圆有关的位置关系
1. 点与圆的位置关系
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.知道点与圆的位置关系,能通过点与圆心的距离与半径的关系判断点与圆的位置关系,反之亦可.
2.知道不在同一直线上的三点确定一个圆,知道三角形的外心、圆的内接三角形等概念,会画三角形的外接圆.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
小玉和小兰设计了一种简易版的飞镖游戏,如下图所示,规则如下:射中红色部分记三分,白色部分记两分,黑色部分记一分,脱靶倒扣一分. 小玉和小兰进行了PK,一人两次机会,黄色飞镖是 小玉射的,红色飞镖是小兰射的,你能分出谁胜谁负吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
规则:射中红色部分记三分,白色部分记两分,黑色部分记一分,脱靶倒扣一分.
小玉:
小兰:
射中红色部分+3,脱靶-1,共计两分;
射中白色部分+2,黑色部分+1,共计三分;
小兰以一分优势获得胜利.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:点和圆的位置关系
问题1:(1)飞镖所在位置有几种可能性呢?
(2)如果把靶子看成是一个圆形,飞镖游戏体现了什么位置关系?
①在圆内;
②在圆上;
③在圆外;
体现了平面内点与圆的位置关系.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)你能将上述三种位置关系转化为数学语言吗?
提示:圆是由所有与定点(圆心)的距离等于定长(半径)的点组成的平面图形.
点与圆心的距离小于半径;
①点P在圆内
②点P在圆上
③点P在圆外
点与圆心的距离等于半径;
点与圆心的距离大于半径;
合作探究
当堂检测
学习目标
课堂总结
自主学习
点和圆的位置关系:
归纳总结
点在圆内
OP < r
OP = r
OP > r
O
P
O
P
O
P
点在圆上
点在圆外
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:不在同一直线上的三点确定圆
问题1:(1)要画出一个确定的圆,需要具备什么条件呢?
(2)过已知点A,你能作出多少个圆呢?
一是圆心,二是半径.
∵圆心与半径都不能确定,
∴可作无数个圆.
·
·
·
·
A
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)过已知点A、B,你能作出多少个圆呢?
∵所作圆经过点A、B,
这些圆的圆心都在线段AB的垂直平分线上.
(4)这些圆的圆心分布有什么特点?
∴圆心O到A、B的距离是相等的
∴可作无数个圆.
·
·
·
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
(5)已知,不在同一条直线上三点A,B,C,过这三点能不能作圆,你能作多少个圆?
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
由于两条垂直平分线的交点只有一个,所以就只能确定一个圆心,也就只能作出一个圆.
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
D
E
G
F
●
O
不在同一条直线上的三个点确定一个圆.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图所示,现在有一个三角形ABC,你能画出这个三角形的外接圆吗?
O
N
M
F
E
A
B
C
1、作线段AB的垂直平分线MN;
2、作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
一个三角形的外接圆也是唯一的.
合作探究
当堂检测
学习目标
课堂总结
自主学习
⊙O叫做△ABC的外接圆;
△ABC叫做⊙O的内接三角形.
三角形外接圆的圆心叫做这个三角形的外心.
三角形的外心是三角形三条边的垂直平分线的交点.
O
A
B
C
归纳总结
三角形的外心到三角形三个顶点的距离相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
Q
P
M
R
A
B
C
A.点P B.点Q
C.点R D.点M
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知如图,矩形ABCD的边长AB=3,BC=4,若以B为圆心,以5为半径作圆,则点A、C、D三点中,在圆上的点是_____;在圆内的点是_______.若以B为圆心,以4为半径作圆,则A、C、D三点中,在圆内的点是_____;在圆上的点是______;在圆外的点是_______.
D
A、C
A
C
D
C
D
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.已知 Rt△ABC中 ,∠C=90°若 AC=12cm,BC=5cm,求的外接圆半径.
解:∵90°的圆周角所对的弦是直径,
故Rt△ABC 的外接圆半径为6.5cm.
∴AB=13cm,OA=6.5cm.
∵∠C=90°,AC=12cm,BC=5cm.
∴AB为圆O的直径,圆心0在AB的中点上,
合作探究
当堂检测
学习目标
课堂总结
自主学习
点和圆的位置关系:
①点P在圆内
②点P在圆上
③点P在圆外
OP < r
OP = r
OP > r
不在同一条直线上的三个点确定一个圆.
三角形外接圆的圆心叫做这个三角形的外心.
