27.1.2 圆的对称性 第1课时 课件(共15张PPT) 华东师大版九年级数学下册
文档属性
| 名称 | 27.1.2 圆的对称性 第1课时 课件(共15张PPT) 华东师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第27章 圆
27.1.2 圆的对称性
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆的对称性,会画圆的对称轴,会找圆的对称中心,会用圆的对称性解决简单的问题.
2.理解弦、弧、圆心角之间的关系,会用它们的关系解决简单的问题.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
情境引入
今天莉莉过生日,有很多人帮她庆生,你能帮她平均分蛋糕吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题一:(1)若只有两个人,你能将蛋糕平均分成两份吗?
即圆是轴对称图形.
O
圆的任意一条直径所在的直线都是它的对称轴.
d
沿直径将蛋糕分开,观察是否能够分成可以完全重合的两部分.
合作探究
当堂检测
学习目标
课堂总结
自主学习
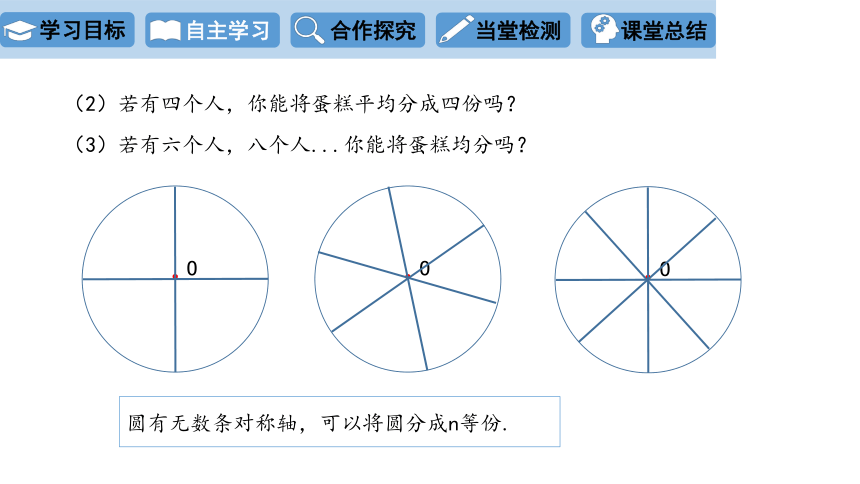
(2)若有四个人,你能将蛋糕平均分成四份吗?
(3)若有六个人,八个人...你能将蛋糕均分吗?
圆有无数条对称轴,可以将圆分成n等份.
O
O
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
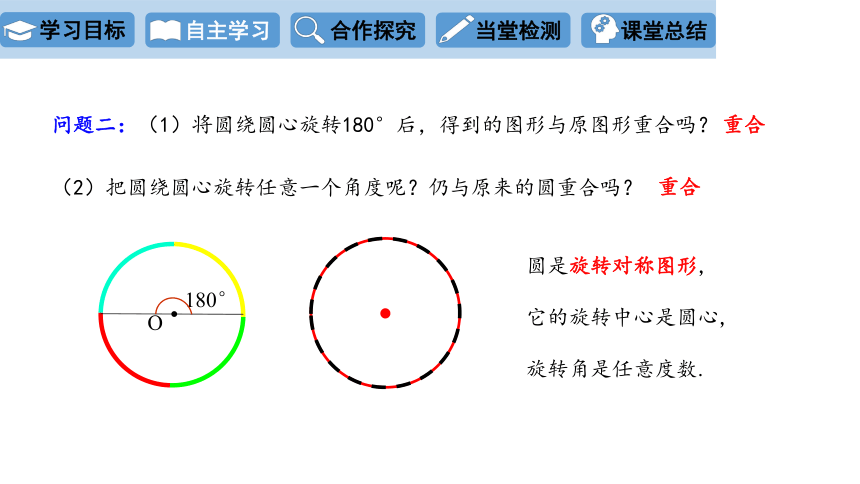
问题二:(1)将圆绕圆心旋转180°后,得到的图形与原图形重合吗?
(2)把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
重合
.
O
180°
·
重合
圆是旋转对称图形,它的旋转中心是圆心,旋转角是任意度数.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题三:(1)将图中的扇形AOB绕点O逆时针旋转β°,你能画出旋转后的扇形A'OB'吗?
(2)在旋转的过程中,圆心角∠AOB,弦AB,弧AB发生了什么变化吗?
∴∠AOB=∠A'OB';
O
A
B
B'
A'
β°
AB=A'B';
︵
AB=A'B';
︵
∵旋转前后图形的大小和形状没有改变
圆心角∠AOB(或弦AB、或弧AB)确定了扇形AOB的大小.
合作探究
当堂检测
学习目标
课堂总结
自主学习
如果弧相等
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
弦所对应的圆心角相等
弦所对应的弧相等
如果圆心角相等
圆心角所对的弧相等
圆心角所对的弦相等
在同一个圆中
归纳总结
弧、弦与圆心角的关系:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:弧、弦与圆心角的关系的应用
问题提出:如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE的度数.
︵
BC=CD=DE,
︵
︵
·
A
O
B
C
D
E
问题探究:分析题目所给的条件.
(1)AB是⊙O 的直径,你能化为数学语言吗?
∠AOE+∠BOE=180°
(2) 你能推出什么信息吗?
︵
BC=CD=DE,
︵
︵
∠BOC=∠COD=∠DOE
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE的度数.
︵
BC=CD=DE,
︵
︵
·
A
O
B
C
D
E
∵AB是⊙O 的直径
∴∠AOE+∠BOE=180°
∵ ∠COD=35°
︵
BC=CD=DE,
︵
︵
∴∠BOC=∠COD=∠DOE=35°
∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-3×35°=75°
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
∴AB=AC
∴∠C=∠B=70°
如图,在⊙O中, ∠B=70°,求∠A的大小.
︵
AB=AC,
︵
解:在⊙O中,
︵
AB=AC,
︵
∴∠A=180°-∠B-∠C=40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:
∴AB=AC.△ABC是等腰三角形.
又∵∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
3.如图,在⊙O中,AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
∵AB=CD,
⌒ ⌒
合作探究
当堂检测
学习目标
课堂总结
自主学习
如果弧相等
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
弦所对应的圆心角相等
弦所对应的弧相等
如果圆心角相等
圆心角所对的弧相等
圆心角所对的弦相等
在同一个圆中
弧、弦与圆心角的关系:
第27章 圆
27.1.2 圆的对称性
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆的对称性,会画圆的对称轴,会找圆的对称中心,会用圆的对称性解决简单的问题.
2.理解弦、弧、圆心角之间的关系,会用它们的关系解决简单的问题.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
情境引入
今天莉莉过生日,有很多人帮她庆生,你能帮她平均分蛋糕吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题一:(1)若只有两个人,你能将蛋糕平均分成两份吗?
即圆是轴对称图形.
O
圆的任意一条直径所在的直线都是它的对称轴.
d
沿直径将蛋糕分开,观察是否能够分成可以完全重合的两部分.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)若有四个人,你能将蛋糕平均分成四份吗?
(3)若有六个人,八个人...你能将蛋糕均分吗?
圆有无数条对称轴,可以将圆分成n等份.
O
O
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题二:(1)将圆绕圆心旋转180°后,得到的图形与原图形重合吗?
(2)把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
重合
.
O
180°
·
重合
圆是旋转对称图形,它的旋转中心是圆心,旋转角是任意度数.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题三:(1)将图中的扇形AOB绕点O逆时针旋转β°,你能画出旋转后的扇形A'OB'吗?
(2)在旋转的过程中,圆心角∠AOB,弦AB,弧AB发生了什么变化吗?
∴∠AOB=∠A'OB';
O
A
B
B'
A'
β°
AB=A'B';
︵
AB=A'B';
︵
∵旋转前后图形的大小和形状没有改变
圆心角∠AOB(或弦AB、或弧AB)确定了扇形AOB的大小.
合作探究
当堂检测
学习目标
课堂总结
自主学习
如果弧相等
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
弦所对应的圆心角相等
弦所对应的弧相等
如果圆心角相等
圆心角所对的弧相等
圆心角所对的弦相等
在同一个圆中
归纳总结
弧、弦与圆心角的关系:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:弧、弦与圆心角的关系的应用
问题提出:如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE的度数.
︵
BC=CD=DE,
︵
︵
·
A
O
B
C
D
E
问题探究:分析题目所给的条件.
(1)AB是⊙O 的直径,你能化为数学语言吗?
∠AOE+∠BOE=180°
(2) 你能推出什么信息吗?
︵
BC=CD=DE,
︵
︵
∠BOC=∠COD=∠DOE
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE的度数.
︵
BC=CD=DE,
︵
︵
·
A
O
B
C
D
E
∵AB是⊙O 的直径
∴∠AOE+∠BOE=180°
∵ ∠COD=35°
︵
BC=CD=DE,
︵
︵
∴∠BOC=∠COD=∠DOE=35°
∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-3×35°=75°
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
∴AB=AC
∴∠C=∠B=70°
如图,在⊙O中, ∠B=70°,求∠A的大小.
︵
AB=AC,
︵
解:在⊙O中,
︵
AB=AC,
︵
∴∠A=180°-∠B-∠C=40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:
∴AB=AC.△ABC是等腰三角形.
又∵∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
3.如图,在⊙O中,AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
∵AB=CD,
⌒ ⌒
合作探究
当堂检测
学习目标
课堂总结
自主学习
如果弧相等
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
弦所对应的圆心角相等
弦所对应的弧相等
如果圆心角相等
圆心角所对的弧相等
圆心角所对的弦相等
在同一个圆中
弧、弦与圆心角的关系:
