第二十七章 圆复习课课件 28张PPT 华东师大版九年级数学下册
文档属性
| 名称 | 第二十七章 圆复习课课件 28张PPT 华东师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 463.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 08:38:34 | ||
图片预览





文档简介
(共28张PPT)
第27章 圆
小结与复习
考点探究
学习目标
课堂总结
知识梳理
1.掌握点和直线与圆的位置关系,并解决相应问题;
2.理解切线的性质和判定,并且掌握切线长定理;
3.理解三角形内切圆及内心的概念,学会运用内心的性质解决问题;
4.掌握正多边形和圆的关系,熟记相应概念.
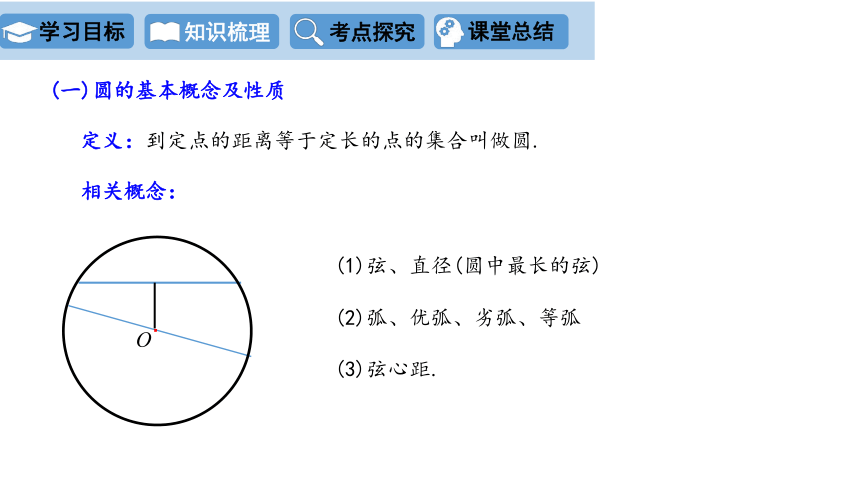
(一)圆的基本概念及性质
定义:到定点的距离等于定长的点的集合叫做圆.
相关概念:
.
O
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距.
考点探究
学习目标
课堂总结
知识梳理
(二)圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,
即圆具有旋转不变性.
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,
那么它们所对应的其余各组量都分别相等.
考点探究
学习目标
课堂总结
知识梳理
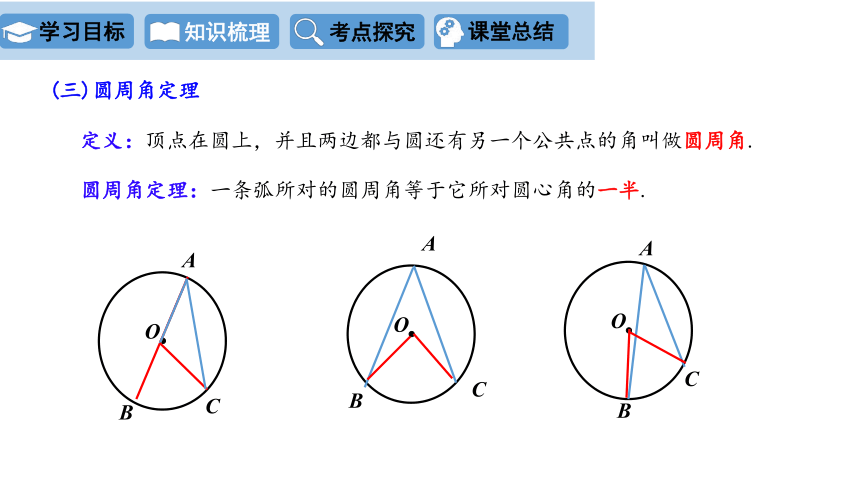
(三)圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
定义:顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
考点探究
学习目标
课堂总结
知识梳理
推论一:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
推论二:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
●A
●B
●C
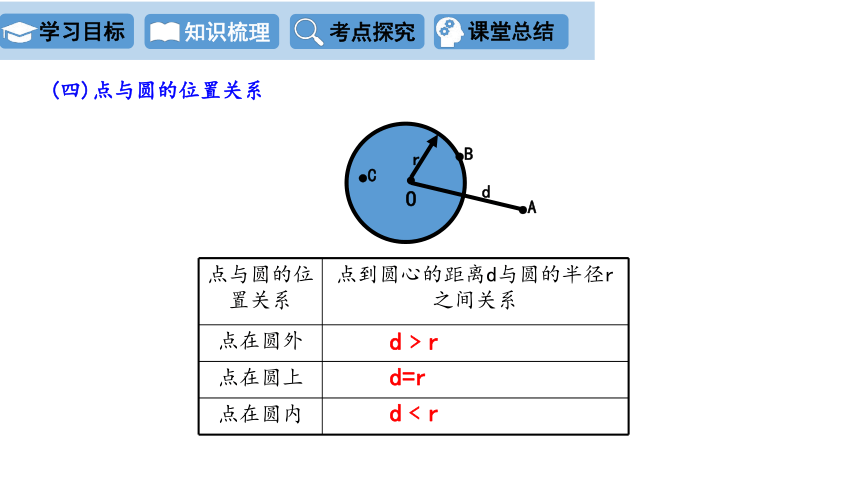
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
(四)点与圆的位置关系
考点探究
学习目标
课堂总结
知识梳理
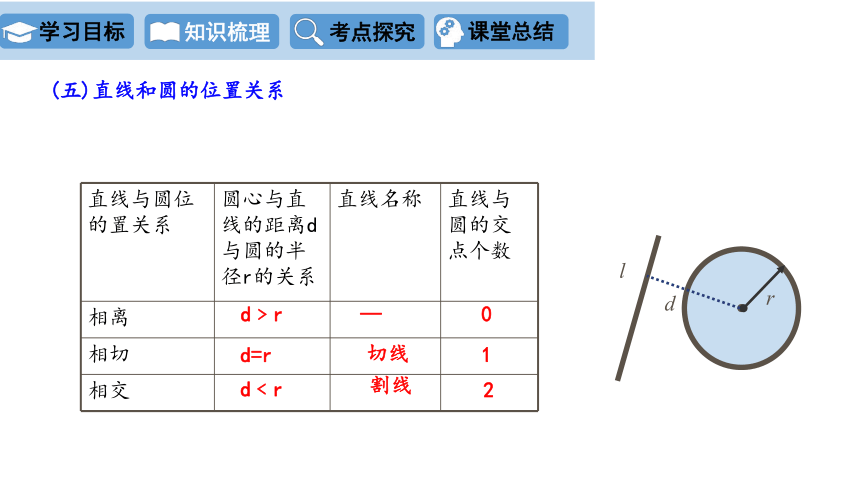
直线与圆位的置关系 圆心与直线的距离d与圆的半径r的关系 直线名称 直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
(五)直线和圆的位置关系
考点探究
学习目标
课堂总结
知识梳理
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端且垂直于半径
(六)切线的性质与判定
考点探究
学习目标
课堂总结
知识梳理
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
2.切线长及切线长定理
考点探究
学习目标
课堂总结
知识梳理
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
┐
A
C
l
┐
┐
D
E
F
三角形的内心到三角形的三边的距离相等.
(七)三角形的内切圆及内心
考点探究
学习目标
课堂总结
知识梳理
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
计算公式:①正多边形的内角和=
②中心角=
(八)正多边形和圆
考点探究
学习目标
课堂总结
知识梳理
考点一:点或直线与圆的位置关系
例1:如图所示,已知∠NON=30°,P是ON上的一点,OP=5㎝,若以P点为圆心,r为半径画圆,使射线OM与⊙P只有一个公共点,求r的值或取值范围.
解:当射线OM与⊙P相切时,射线OM
与⊙P只有一个公共点.
过点P作PA⊥OM于A,如图1所示.
在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
图1
考点探究
学习目标
课堂总结
知识梳理
当射线OM与⊙P相交且点O在⊙P内时,射线OM与⊙P只有一个公共点.如图2所示.
∵射线OM与⊙P相交,则r>2.5㎝ ···①
又∵点O在⊙P内,则r>OP,即r>5㎝ ···②
综合①、②可得r>5.
综上所述,当射线OM与⊙P只有一个公共点时,
r=2.5㎝或r>5㎝.
图2
考点探究
学习目标
课堂总结
知识梳理
本题之类的题目中,常因混淆了“直线与圆只有一个交点”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区别.实际上,当直线与圆只有一个交点时,直线与圆一定相切,而线段与圆只有一个交点或射线与圆只有一个交点时,它们与圆的位置关系可能相切,也可能是相交.
方法小结:
考点探究
学习目标
课堂总结
知识梳理
1.如图,直线l:y= x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,则m的值为_______.
针对训练
考点探究
学习目标
课堂总结
知识梳理
考点二:切线的性质与判定
例2:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.(1)若AD=3,BD=4,求边BC的长.
解:(1)∵AB是直径,∴∠ADB=90°.
∵AD=3,BD=4,∴AB=5.
∵∠CDB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
考点探究
学习目标
课堂总结
知识梳理
例2:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.(2)取BC的中点E,连接ED,试证明ED与☉O相切.
又∵∠OBD+∠DBC=90°,∠C+∠DBC=90°,
∴∠C=∠OBD,∴∠BDO=∠CDE.
∵AB是直径,∴∠ADB=90°,
∴∠BDC=90°,即∠BDE+∠CDE=90°.
∴∠BDE+∠BDO=90°,即∠ODE=90°.∴ED与☉O相切.
证明:连接OD,在Rt△BDC中,
∵E是BC的中点,∴CE=DE,∴∠C=∠CDE.
又OD=OB,∴∠ODB=∠OBD.
考点探究
学习目标
课堂总结
知识梳理
2.如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
4或8
解析: 根本题应分为两种情况:(1)☉P在直线CD下面与直线CD相切;(2)☉P在直线CD上面与直线CD相切.
A
B
D
C
P
P2
P1
O
针对训练
考点探究
学习目标
课堂总结
知识梳理
3.如图,线段AB是直径,点D是☉O上一点, ∠CDB=20 °,过点C作☉O的切线交AB的延长线于点E,则∠E等于 .
O
C
A
B
E
D
50°
考点探究
学习目标
课堂总结
知识梳理
4.如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
问:BC与⊙O是否相切?
解:BC与⊙O相切.
∴BC与⊙O相切.
理由:∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°.
又DE平分CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∠ODB=∠OBD,∠ODB+∠EDB=90°
∴∠OBD+∠DBE=90°,即∠ABC=90°.
考点探究
学习目标
课堂总结
知识梳理
考点三:正多边形与圆
例3:如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.⑴求正方形EFGH的面积;
解:⑴∵正六边形的边长与其半径相等,
∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
考点探究
学习目标
课堂总结
知识梳理
例3:如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.(2)连接OF、OG,求∠OGF的度数.
解:∵正六边形的边长与其半径相等,
∴∠OFE=60°.
∴正方形的内角是90°,
∵∠OFG=∠OFE +∠EFG=60°+90°=150°.
由⑴得OF=FG,∴∠OGF= (180°-∠OFG)
= (180°-150°)=15°.
考点探究
学习目标
课堂总结
知识梳理
5.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°则 的长( )
B
针对训练
考点探究
学习目标
课堂总结
知识梳理
6.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,
已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
考点探究
学习目标
课堂总结
知识梳理
考点五:与圆有关的计算
7.如图,半径为1的☉O与正五边形ABCDE相切于点A,C,则劣弧AC的长度为( )
针对训练
B
考点探究
学习目标
课堂总结
知识梳理
8.如图,AB是☉O的直径,E为BC的中点,AB=4,
∠BED=120°,求图中阴影部分的面积.
∴阴影部分的面积=S△EDC= .
∴△ABC是等边三角形,边长是4,△EDC是等边三角形,边长是2,
解:连接AE,OD,OE,
∵AB是☉O的直径,∴∠AEB=90°,
又∵∠BED=120°,∴∠AED=30°,
∵OA=OD,∴△AOD是等边三角形,∠OAD=60°.
∵E为BC的中点,∠AEB=90°,∴AB=AC,
∴∠BOE=∠EOD=60°,弧BE和弦BE围成的面积,与弧DE和弦DE围成的面积相等.
∴∠AOD=2∠AED=60°.
考点探究
学习目标
课堂总结
知识梳理
圆
与圆有关的位置关系
与圆有关的计算
点与圆的位置关系
点在圆环内:
r ≤d ≤R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;
无公共点,作垂直,证半径;
见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
第27章 圆
小结与复习
考点探究
学习目标
课堂总结
知识梳理
1.掌握点和直线与圆的位置关系,并解决相应问题;
2.理解切线的性质和判定,并且掌握切线长定理;
3.理解三角形内切圆及内心的概念,学会运用内心的性质解决问题;
4.掌握正多边形和圆的关系,熟记相应概念.
(一)圆的基本概念及性质
定义:到定点的距离等于定长的点的集合叫做圆.
相关概念:
.
O
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距.
考点探究
学习目标
课堂总结
知识梳理
(二)圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,
即圆具有旋转不变性.
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,
那么它们所对应的其余各组量都分别相等.
考点探究
学习目标
课堂总结
知识梳理
(三)圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
定义:顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
考点探究
学习目标
课堂总结
知识梳理
推论一:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
推论二:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
(四)点与圆的位置关系
考点探究
学习目标
课堂总结
知识梳理
直线与圆位的置关系 圆心与直线的距离d与圆的半径r的关系 直线名称 直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
(五)直线和圆的位置关系
考点探究
学习目标
课堂总结
知识梳理
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端且垂直于半径
(六)切线的性质与判定
考点探究
学习目标
课堂总结
知识梳理
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
2.切线长及切线长定理
考点探究
学习目标
课堂总结
知识梳理
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
┐
A
C
l
┐
┐
D
E
F
三角形的内心到三角形的三边的距离相等.
(七)三角形的内切圆及内心
考点探究
学习目标
课堂总结
知识梳理
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
计算公式:①正多边形的内角和=
②中心角=
(八)正多边形和圆
考点探究
学习目标
课堂总结
知识梳理
考点一:点或直线与圆的位置关系
例1:如图所示,已知∠NON=30°,P是ON上的一点,OP=5㎝,若以P点为圆心,r为半径画圆,使射线OM与⊙P只有一个公共点,求r的值或取值范围.
解:当射线OM与⊙P相切时,射线OM
与⊙P只有一个公共点.
过点P作PA⊥OM于A,如图1所示.
在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
图1
考点探究
学习目标
课堂总结
知识梳理
当射线OM与⊙P相交且点O在⊙P内时,射线OM与⊙P只有一个公共点.如图2所示.
∵射线OM与⊙P相交,则r>2.5㎝ ···①
又∵点O在⊙P内,则r>OP,即r>5㎝ ···②
综合①、②可得r>5.
综上所述,当射线OM与⊙P只有一个公共点时,
r=2.5㎝或r>5㎝.
图2
考点探究
学习目标
课堂总结
知识梳理
本题之类的题目中,常因混淆了“直线与圆只有一个交点”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区别.实际上,当直线与圆只有一个交点时,直线与圆一定相切,而线段与圆只有一个交点或射线与圆只有一个交点时,它们与圆的位置关系可能相切,也可能是相交.
方法小结:
考点探究
学习目标
课堂总结
知识梳理
1.如图,直线l:y= x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,则m的值为_______.
针对训练
考点探究
学习目标
课堂总结
知识梳理
考点二:切线的性质与判定
例2:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.(1)若AD=3,BD=4,求边BC的长.
解:(1)∵AB是直径,∴∠ADB=90°.
∵AD=3,BD=4,∴AB=5.
∵∠CDB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
考点探究
学习目标
课堂总结
知识梳理
例2:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.(2)取BC的中点E,连接ED,试证明ED与☉O相切.
又∵∠OBD+∠DBC=90°,∠C+∠DBC=90°,
∴∠C=∠OBD,∴∠BDO=∠CDE.
∵AB是直径,∴∠ADB=90°,
∴∠BDC=90°,即∠BDE+∠CDE=90°.
∴∠BDE+∠BDO=90°,即∠ODE=90°.∴ED与☉O相切.
证明:连接OD,在Rt△BDC中,
∵E是BC的中点,∴CE=DE,∴∠C=∠CDE.
又OD=OB,∴∠ODB=∠OBD.
考点探究
学习目标
课堂总结
知识梳理
2.如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
4或8
解析: 根本题应分为两种情况:(1)☉P在直线CD下面与直线CD相切;(2)☉P在直线CD上面与直线CD相切.
A
B
D
C
P
P2
P1
O
针对训练
考点探究
学习目标
课堂总结
知识梳理
3.如图,线段AB是直径,点D是☉O上一点, ∠CDB=20 °,过点C作☉O的切线交AB的延长线于点E,则∠E等于 .
O
C
A
B
E
D
50°
考点探究
学习目标
课堂总结
知识梳理
4.如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
问:BC与⊙O是否相切?
解:BC与⊙O相切.
∴BC与⊙O相切.
理由:∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°.
又DE平分CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∠ODB=∠OBD,∠ODB+∠EDB=90°
∴∠OBD+∠DBE=90°,即∠ABC=90°.
考点探究
学习目标
课堂总结
知识梳理
考点三:正多边形与圆
例3:如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.⑴求正方形EFGH的面积;
解:⑴∵正六边形的边长与其半径相等,
∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
考点探究
学习目标
课堂总结
知识梳理
例3:如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.(2)连接OF、OG,求∠OGF的度数.
解:∵正六边形的边长与其半径相等,
∴∠OFE=60°.
∴正方形的内角是90°,
∵∠OFG=∠OFE +∠EFG=60°+90°=150°.
由⑴得OF=FG,∴∠OGF= (180°-∠OFG)
= (180°-150°)=15°.
考点探究
学习目标
课堂总结
知识梳理
5.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°则 的长( )
B
针对训练
考点探究
学习目标
课堂总结
知识梳理
6.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,
已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
考点探究
学习目标
课堂总结
知识梳理
考点五:与圆有关的计算
7.如图,半径为1的☉O与正五边形ABCDE相切于点A,C,则劣弧AC的长度为( )
针对训练
B
考点探究
学习目标
课堂总结
知识梳理
8.如图,AB是☉O的直径,E为BC的中点,AB=4,
∠BED=120°,求图中阴影部分的面积.
∴阴影部分的面积=S△EDC= .
∴△ABC是等边三角形,边长是4,△EDC是等边三角形,边长是2,
解:连接AE,OD,OE,
∵AB是☉O的直径,∴∠AEB=90°,
又∵∠BED=120°,∴∠AED=30°,
∵OA=OD,∴△AOD是等边三角形,∠OAD=60°.
∵E为BC的中点,∠AEB=90°,∴AB=AC,
∴∠BOE=∠EOD=60°,弧BE和弦BE围成的面积,与弧DE和弦DE围成的面积相等.
∴∠AOD=2∠AED=60°.
考点探究
学习目标
课堂总结
知识梳理
圆
与圆有关的位置关系
与圆有关的计算
点与圆的位置关系
点在圆环内:
r ≤d ≤R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;
无公共点,作垂直,证半径;
见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
