鲁教版(五四学制)数学七年级下册期末综合素质评价(含解析)
文档属性
| 名称 | 鲁教版(五四学制)数学七年级下册期末综合素质评价(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 422.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 17:34:57 | ||
图片预览




文档简介
期末综合素质评价
一、选择题(每题3分,共36分)
1.一个不透明的袋子中有3个白球、2个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是黄球的概率为( )
A. B. C. D.
2.已知a>b,则一定有-4a□-4b,“□”中应填的符号是( )
A.> B.< C.≥ D.=
3.【2022·德阳】下列事件中,属于必然事件的是( )
A.抛掷硬币时,正面朝上
B.明天太阳从东方升起
C.经过红绿灯路口,遇到红灯
D.玩“石头、剪刀、布”游戏时,对方出“剪刀”
4.如图,直线m,n分别截∠A的两边,且m∥n.下列各角的度数关系中正确的是( )
A. ∠2+∠5>180° B.∠2+∠3<180°
C.∠1+∠6>180° D.∠3+∠4<180°
5.如图,已知∠C=∠D=90°,有4个可添加的条件:①AC=BD;②BC=AD;③∠CAB=∠DBA;④∠CBA=∠DAB.能使△ABC≌△BAD的条件有( )
A.1个 B.2个 C.3个 D.4个
6.【2022·泸州】如图,直线a∥b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是( )
A.30° B.40°
C.50° D.70°
7.关于x,y的方程组的解为若点P(a,b)总在直线y=x的上方,那么k的取值范围是( )
A.k>1 B.k>-1 C.k<1 D.k<-1
8.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是( )
A.5
B.10
C.12
D.13
9.【数学文化】【2022·遂宁】《九章算术》是我国古代数学的经典著作,书中记载了这样一个题目:今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?其大意是:甲袋中装有黄金9枚(每枚黄金质量相同),乙袋中装有白银11枚(每枚白银质量相同),称重两袋质量相等,两袋互换一枚后,甲袋比乙袋轻了13两(袋子质量忽略不计),问黄金、白银每枚各重几两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为( )
A. B.
C. D.
10.在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示,根据图象得到的正确结论是( )
A.方程组的解为
B.n+b<0
C.当x>-3时,ax+b>mx+n
D.当x=0时,ax+b=-1
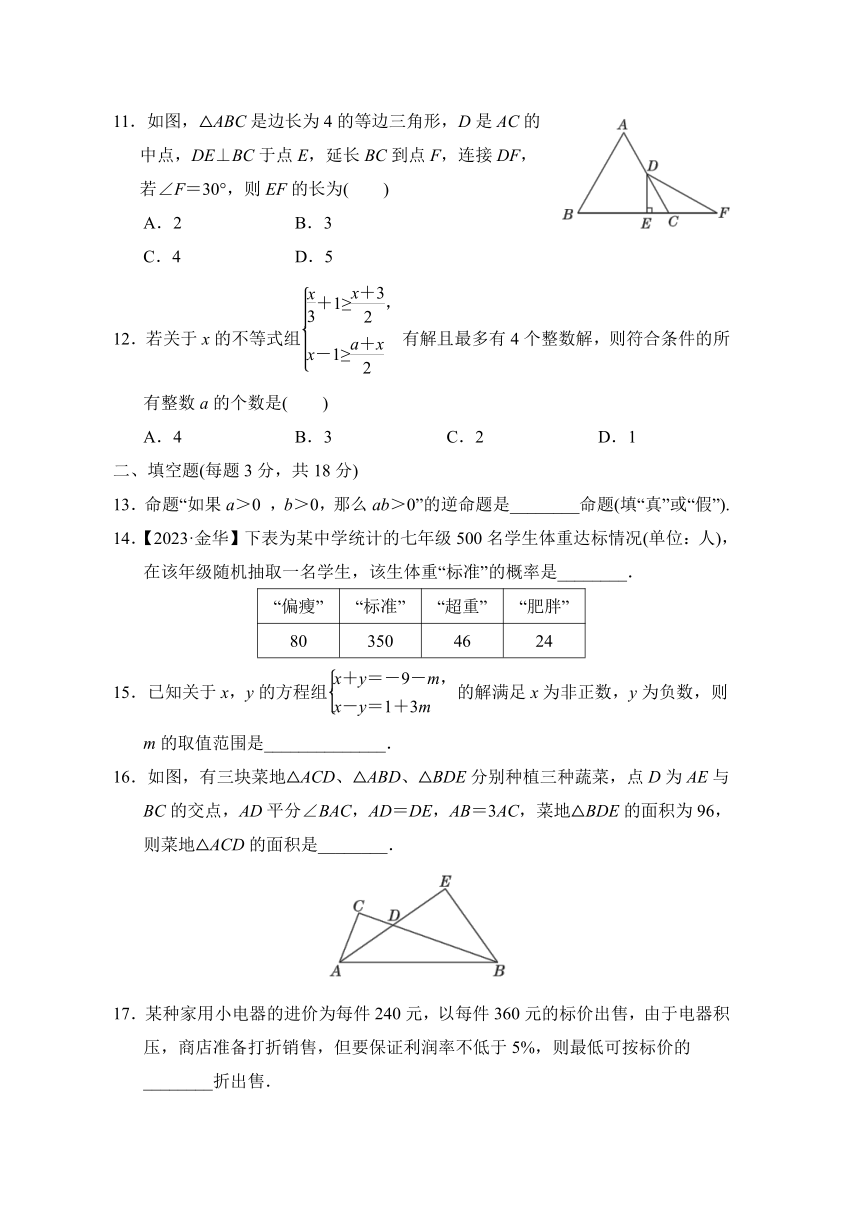
11.如图,△ABC是边长为4的等边三角形,D是AC的中点,DE⊥BC于点E,延长BC到点F,连接DF,若∠F=30°,则EF的长为( )
A.2 B.3
C.4 D.5
12.若关于x的不等式组有解且最多有4个整数解,则符合条件的所有整数a的个数是( )
A.4 B.3 C.2 D.1
二、填空题(每题3分,共18分)
13.命题“如果a>0 ,b>0,那么ab>0”的逆命题是________命题(填“真”或“假”).
14.【2023·金华】下表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是________.
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
15.已知关于x,y的方程组的解满足x为非正数,y为负数,则m的取值范围是______________.
16.如图,有三块菜地△ACD、△ABD、△BDE分别种植三种蔬菜,点D为AE与BC的交点,AD平分∠BAC,AD=DE,AB=3AC,菜地△BDE的面积为96,则菜地△ACD的面积是________.
17.某种家用小电器的进价为每件240元,以每件360元的标价出售,由于电器积压,商店准备打折销售,但要保证利润率不低于5%,则最低可按标价的________折出售.
18.如图,MN∥EF,点C为两直线之间的点,若∠MAC的平分线与∠FBC的平分线所在的直线相交于点D,则∠ACB与∠ADB之间的数量关系是______________________.
三、解答题(23题10分, 24,25题每题12分,其余每题8分,共66分)
19.(1)【2022·台州】解方程组:
(2)解不等式组:并将解集在数轴上表示出来.
20.【2023·大连】如图,在△ABC和△ADE中,延长BC交DE于F.BC=DE, AC=AE,∠ACF+∠AED=180°.求证:AB=AD.
21.如图所示的转盘被分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,指针会指向其中的某个扇形,并相应得到一个数(指针指向分界线时,则重转).
(1)事件“转动一次转盘,得到的数恰好是0”发生的概率是________.
(2)写出此情境下一个不可能发生的事件.
22.如图,在平面直角坐标系中,直线y=x+3与x轴交于点A,且经过点B(2,m),已知点C的坐标是(5,0).
(1)求直线BC的表达式.
(2)若D为线段BC上一点,且S△ABD=S△AOB,求点D的坐标.
23.某快递公司为了提高工作效率,计划购买A,B两种型号的机器人来搬运货物,已知每台A型机器人比每台B型机器人每天多搬运20吨,并且3台A型机器人和2台B型机器人每天共搬运货物460吨.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨.
(2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公司计划采购A,B两种型号的机器人共20台,必须满足每天搬运的货物不低于1 800吨,则A,B两种型号的机器人分别采购多少台时,所需费用最低?最低费用是多少?
24.如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,连接CD,BE,相交于点F.
(1)求证:BE⊥CD.
(2)若∠BAC=30°,试判断△CBD的形状,并说明理由.
25.在△ABC中,BO⊥AC于点O,AO=BO=3,OC=1.
(1)如图①,过点A作AH⊥BC于点H,交BO于点P,连接OH.
①求线段OP的长度;
②求证:∠OHP=45°;
(2)如图②,若D为AB的中点,点M为线段BO延长线上一动点,连接MD,过点D作DN⊥DM交线段CA的延长线于点N,则S△BDM-S△ADN的值是否发生改变?若改变,求该式子的值的变化范围;若不改变,求该式子的值.
答案
一、1.B 2.B 3.B 4.A 5.D 6.B
7.B 【点拨】解方程组
得
∵点P(a,b)总在直线y=x的上方,
∴b>a,∴k+1>-k-1,
解得k>-1.
8.D 9.D
10.B 【点拨】∵一次函数y=ax+b与y=mx+n(a<m<0)的图象交于点(-3,2),
∴方程组的解为
由图象可知b=-2,0<n<1,∴n+b<0.
由图象可知当x>-3时,ax+b<mx+n.
∵一次函数y=ax+b的图象过点(0,-2),
∴当x=0时,ax+b=-2.
11.B 【点拨】∵△ABC是边长为4的等边三角形,
∴AC=4,∠ACB=60°.∵∠F=30°,
∴∠CDF=∠ACB-∠F=60°-30°=30°,
∴∠CDF=∠F,∴CD=CF.
∵D是AC的中点,∴AD=CD=AC=2,
∴CF=2.在Rt△DEC中,∠DCE=60°,
∴∠CDE=30°,∴EC=CD=1,
∴EF=EC+CF=1+2=3.
12.A 【点拨】解不等式+1≥,得x≤-3,
解不等式x-1≥,得x≥a+2,
∴不等式组的解集为a+2≤x≤-3.
∵该不等式组有解且最多有4个整数解,
∴-7∴-9∴符合条件的所有整数a的个数为4.
二、13.假 14. 15.-<m≤4
16.32 【点拨】∵AD=DE,S△BDE=96,
∴S△ABD=S△BDE=96.
过点D分别作DG⊥AC于点G,DF⊥AB于点F.
∵AD平分∠BAC,∴DG=DF.
又∵AB=3AC,∴S△ACD=S△ABD=×96=32.
17.七
18. ∠ACB=180°-2∠ADB
【点拨】如图,过点C作CG∥MN,过点D作DH∥MN .
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,∠6=∠4,∠FBC=∠5,
∴∠ACB=∠4+∠5=∠6+∠FBC,
∠ADB=∠ADH-∠BDH=∠1-∠2.
∵∠MAC的平分线与∠FBC的平分线所在直线相交于点D,
∴∠MAC=2∠1,∠FBC=2∠3=2∠2,
∴∠ACB=∠6+∠FBC=180°-∠MAC+2∠2=180°-2∠1+2∠2=180°-2(∠1-∠2)=180°-2∠ADB.
三、19.【解】(1)
②-①,得y=1.把y=1代入①,得x+2=4,解得x=2.
所以原方程组的解为
(2)解不等式①,得x<3.解不等式②,得x≥1.
所以不等式组的解集是1≤x<3.
将解集表示在数轴上如图所示.
20.【证明】∵∠ACB+∠ACF=180°,
∠ACF+∠AED=180°,
∴∠ACB=∠AED.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),∴AB=AD.
21.【解】(1)
(2)事件“转动一次转盘,得到的数恰好是3”.(答案不唯一)
22.【解】(1)将点B(2,m)的坐标代入y=x+3,得m=×2+3=6,∴B(2,6).
设直线BC的表达式为y=kx+b,
将点B(2,6),C(5,0)的坐标分别代入y=kx+b,
得解得
∴直线BC的表达式为y=-2x+10.
(2)如图,连接OD,由S△ABD=S△AOB可知OD∥AB,
∴直线OD的表达式为y=x,
联立方程
得∴点D的坐标为.
23.【解】(1)设每台A型机器人每天搬运货物x吨,每台B型机器人每天搬运货物y吨,
根据题意得
解得
答:每台A型机器人每天搬运货物100吨,每台B型机器人每天搬运货物 80吨.
(2)设A型机器人采购m台,B型机器人采购(20-m)台,总费用为w万元,
则w=3m+2(20-m)=m+40.
根据题意得100m+80(20-m)≥1 800,解得m≥10.
在w=m+40中,
∵1>0,∴w随着m的增大而增大.
∴当m=10时,w有最小值,w最小=10+40=50.
此时20-m=10.
∴当A型机器人采购10台,B型机器人采购10台时,所需费用最低,最低费用是50万元.
24.(1)【证明】∵∠ACB=90°,且DE⊥AB,
∴∠EDB=∠ACB=90°.
在Rt△EBC和Rt△EBD中,
∴Rt△EBC≌Rt△EBD,
∴∠CBE=∠DBE.
∵BD=BC,∴△BDC是等腰三角形.
∴BF⊥CD,即BE⊥CD.
(2)【解】△CBD是等边三角形.理由如下:
∵∠CAB=30°,∠ACB=90°,
∴∠CBD=60°.
又∵BD=BC,∴△CBD是等边三角形.
25.(1)①【解】∵BO⊥AC,AH⊥BC,
∴∠AOP=∠BOC=∠AHC=90°,
∴∠OBC+∠C=∠OAP+∠C=90°,
∴∠OBC=∠OAP.
在△OAP和△OBC中,
∴△OAP≌△OBC(ASA),∴OP=OC=1.
②【证明】如图①,过点O分别作OM⊥BC于点M,ON⊥AH于点N, 则 ∠OMC=∠ONP=90°.
易知∠MON=90°,
∴∠COM=90°-∠MOP=∠PON.
在△COM和△PON中,
∴△COM≌△PON(AAS).∴OM=ON.
又∵OM⊥BC,ON⊥AH.∴HO平分∠AHC.
∴∠OHP=∠AHC=45°.
(2)【解】S△BDM-S△ADN的值不发生改变.
如图②,连接OD.
∵BO⊥AC,OA=OB,∴∠BOA=90°,
∠BAO=∠ABO=45°.
∵D为AB的中点,∴∠DOA=45°.
∴∠DOM=90°+45°=135°,∠DAN=135°,∠ADO=90°,
∴∠DAN=∠DOM.∵MD⊥ND,∴∠MDN=90°.
∴∠NDA=90°-∠MDA=∠MDO.
在△ODM和△ADN中,
∴△ODM≌△ADN(ASA),∴S△ODM=S△ADN,
∴S△BDM-S△ADN=S△BDM-S△ODM=S△BOD=S△AOB=×AO·BO=××3×3=.
一、选择题(每题3分,共36分)
1.一个不透明的袋子中有3个白球、2个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是黄球的概率为( )
A. B. C. D.
2.已知a>b,则一定有-4a□-4b,“□”中应填的符号是( )
A.> B.< C.≥ D.=
3.【2022·德阳】下列事件中,属于必然事件的是( )
A.抛掷硬币时,正面朝上
B.明天太阳从东方升起
C.经过红绿灯路口,遇到红灯
D.玩“石头、剪刀、布”游戏时,对方出“剪刀”
4.如图,直线m,n分别截∠A的两边,且m∥n.下列各角的度数关系中正确的是( )
A. ∠2+∠5>180° B.∠2+∠3<180°
C.∠1+∠6>180° D.∠3+∠4<180°
5.如图,已知∠C=∠D=90°,有4个可添加的条件:①AC=BD;②BC=AD;③∠CAB=∠DBA;④∠CBA=∠DAB.能使△ABC≌△BAD的条件有( )
A.1个 B.2个 C.3个 D.4个
6.【2022·泸州】如图,直线a∥b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是( )
A.30° B.40°
C.50° D.70°
7.关于x,y的方程组的解为若点P(a,b)总在直线y=x的上方,那么k的取值范围是( )
A.k>1 B.k>-1 C.k<1 D.k<-1
8.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是( )
A.5
B.10
C.12
D.13
9.【数学文化】【2022·遂宁】《九章算术》是我国古代数学的经典著作,书中记载了这样一个题目:今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?其大意是:甲袋中装有黄金9枚(每枚黄金质量相同),乙袋中装有白银11枚(每枚白银质量相同),称重两袋质量相等,两袋互换一枚后,甲袋比乙袋轻了13两(袋子质量忽略不计),问黄金、白银每枚各重几两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为( )
A. B.
C. D.
10.在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示,根据图象得到的正确结论是( )
A.方程组的解为
B.n+b<0
C.当x>-3时,ax+b>mx+n
D.当x=0时,ax+b=-1
11.如图,△ABC是边长为4的等边三角形,D是AC的中点,DE⊥BC于点E,延长BC到点F,连接DF,若∠F=30°,则EF的长为( )
A.2 B.3
C.4 D.5
12.若关于x的不等式组有解且最多有4个整数解,则符合条件的所有整数a的个数是( )
A.4 B.3 C.2 D.1
二、填空题(每题3分,共18分)
13.命题“如果a>0 ,b>0,那么ab>0”的逆命题是________命题(填“真”或“假”).
14.【2023·金华】下表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是________.
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
15.已知关于x,y的方程组的解满足x为非正数,y为负数,则m的取值范围是______________.
16.如图,有三块菜地△ACD、△ABD、△BDE分别种植三种蔬菜,点D为AE与BC的交点,AD平分∠BAC,AD=DE,AB=3AC,菜地△BDE的面积为96,则菜地△ACD的面积是________.
17.某种家用小电器的进价为每件240元,以每件360元的标价出售,由于电器积压,商店准备打折销售,但要保证利润率不低于5%,则最低可按标价的________折出售.
18.如图,MN∥EF,点C为两直线之间的点,若∠MAC的平分线与∠FBC的平分线所在的直线相交于点D,则∠ACB与∠ADB之间的数量关系是______________________.
三、解答题(23题10分, 24,25题每题12分,其余每题8分,共66分)
19.(1)【2022·台州】解方程组:
(2)解不等式组:并将解集在数轴上表示出来.
20.【2023·大连】如图,在△ABC和△ADE中,延长BC交DE于F.BC=DE, AC=AE,∠ACF+∠AED=180°.求证:AB=AD.
21.如图所示的转盘被分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,指针会指向其中的某个扇形,并相应得到一个数(指针指向分界线时,则重转).
(1)事件“转动一次转盘,得到的数恰好是0”发生的概率是________.
(2)写出此情境下一个不可能发生的事件.
22.如图,在平面直角坐标系中,直线y=x+3与x轴交于点A,且经过点B(2,m),已知点C的坐标是(5,0).
(1)求直线BC的表达式.
(2)若D为线段BC上一点,且S△ABD=S△AOB,求点D的坐标.
23.某快递公司为了提高工作效率,计划购买A,B两种型号的机器人来搬运货物,已知每台A型机器人比每台B型机器人每天多搬运20吨,并且3台A型机器人和2台B型机器人每天共搬运货物460吨.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨.
(2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公司计划采购A,B两种型号的机器人共20台,必须满足每天搬运的货物不低于1 800吨,则A,B两种型号的机器人分别采购多少台时,所需费用最低?最低费用是多少?
24.如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,连接CD,BE,相交于点F.
(1)求证:BE⊥CD.
(2)若∠BAC=30°,试判断△CBD的形状,并说明理由.
25.在△ABC中,BO⊥AC于点O,AO=BO=3,OC=1.
(1)如图①,过点A作AH⊥BC于点H,交BO于点P,连接OH.
①求线段OP的长度;
②求证:∠OHP=45°;
(2)如图②,若D为AB的中点,点M为线段BO延长线上一动点,连接MD,过点D作DN⊥DM交线段CA的延长线于点N,则S△BDM-S△ADN的值是否发生改变?若改变,求该式子的值的变化范围;若不改变,求该式子的值.
答案
一、1.B 2.B 3.B 4.A 5.D 6.B
7.B 【点拨】解方程组
得
∵点P(a,b)总在直线y=x的上方,
∴b>a,∴k+1>-k-1,
解得k>-1.
8.D 9.D
10.B 【点拨】∵一次函数y=ax+b与y=mx+n(a<m<0)的图象交于点(-3,2),
∴方程组的解为
由图象可知b=-2,0<n<1,∴n+b<0.
由图象可知当x>-3时,ax+b<mx+n.
∵一次函数y=ax+b的图象过点(0,-2),
∴当x=0时,ax+b=-2.
11.B 【点拨】∵△ABC是边长为4的等边三角形,
∴AC=4,∠ACB=60°.∵∠F=30°,
∴∠CDF=∠ACB-∠F=60°-30°=30°,
∴∠CDF=∠F,∴CD=CF.
∵D是AC的中点,∴AD=CD=AC=2,
∴CF=2.在Rt△DEC中,∠DCE=60°,
∴∠CDE=30°,∴EC=CD=1,
∴EF=EC+CF=1+2=3.
12.A 【点拨】解不等式+1≥,得x≤-3,
解不等式x-1≥,得x≥a+2,
∴不等式组的解集为a+2≤x≤-3.
∵该不等式组有解且最多有4个整数解,
∴-7
二、13.假 14. 15.-<m≤4
16.32 【点拨】∵AD=DE,S△BDE=96,
∴S△ABD=S△BDE=96.
过点D分别作DG⊥AC于点G,DF⊥AB于点F.
∵AD平分∠BAC,∴DG=DF.
又∵AB=3AC,∴S△ACD=S△ABD=×96=32.
17.七
18. ∠ACB=180°-2∠ADB
【点拨】如图,过点C作CG∥MN,过点D作DH∥MN .
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,∠6=∠4,∠FBC=∠5,
∴∠ACB=∠4+∠5=∠6+∠FBC,
∠ADB=∠ADH-∠BDH=∠1-∠2.
∵∠MAC的平分线与∠FBC的平分线所在直线相交于点D,
∴∠MAC=2∠1,∠FBC=2∠3=2∠2,
∴∠ACB=∠6+∠FBC=180°-∠MAC+2∠2=180°-2∠1+2∠2=180°-2(∠1-∠2)=180°-2∠ADB.
三、19.【解】(1)
②-①,得y=1.把y=1代入①,得x+2=4,解得x=2.
所以原方程组的解为
(2)解不等式①,得x<3.解不等式②,得x≥1.
所以不等式组的解集是1≤x<3.
将解集表示在数轴上如图所示.
20.【证明】∵∠ACB+∠ACF=180°,
∠ACF+∠AED=180°,
∴∠ACB=∠AED.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),∴AB=AD.
21.【解】(1)
(2)事件“转动一次转盘,得到的数恰好是3”.(答案不唯一)
22.【解】(1)将点B(2,m)的坐标代入y=x+3,得m=×2+3=6,∴B(2,6).
设直线BC的表达式为y=kx+b,
将点B(2,6),C(5,0)的坐标分别代入y=kx+b,
得解得
∴直线BC的表达式为y=-2x+10.
(2)如图,连接OD,由S△ABD=S△AOB可知OD∥AB,
∴直线OD的表达式为y=x,
联立方程
得∴点D的坐标为.
23.【解】(1)设每台A型机器人每天搬运货物x吨,每台B型机器人每天搬运货物y吨,
根据题意得
解得
答:每台A型机器人每天搬运货物100吨,每台B型机器人每天搬运货物 80吨.
(2)设A型机器人采购m台,B型机器人采购(20-m)台,总费用为w万元,
则w=3m+2(20-m)=m+40.
根据题意得100m+80(20-m)≥1 800,解得m≥10.
在w=m+40中,
∵1>0,∴w随着m的增大而增大.
∴当m=10时,w有最小值,w最小=10+40=50.
此时20-m=10.
∴当A型机器人采购10台,B型机器人采购10台时,所需费用最低,最低费用是50万元.
24.(1)【证明】∵∠ACB=90°,且DE⊥AB,
∴∠EDB=∠ACB=90°.
在Rt△EBC和Rt△EBD中,
∴Rt△EBC≌Rt△EBD,
∴∠CBE=∠DBE.
∵BD=BC,∴△BDC是等腰三角形.
∴BF⊥CD,即BE⊥CD.
(2)【解】△CBD是等边三角形.理由如下:
∵∠CAB=30°,∠ACB=90°,
∴∠CBD=60°.
又∵BD=BC,∴△CBD是等边三角形.
25.(1)①【解】∵BO⊥AC,AH⊥BC,
∴∠AOP=∠BOC=∠AHC=90°,
∴∠OBC+∠C=∠OAP+∠C=90°,
∴∠OBC=∠OAP.
在△OAP和△OBC中,
∴△OAP≌△OBC(ASA),∴OP=OC=1.
②【证明】如图①,过点O分别作OM⊥BC于点M,ON⊥AH于点N, 则 ∠OMC=∠ONP=90°.
易知∠MON=90°,
∴∠COM=90°-∠MOP=∠PON.
在△COM和△PON中,
∴△COM≌△PON(AAS).∴OM=ON.
又∵OM⊥BC,ON⊥AH.∴HO平分∠AHC.
∴∠OHP=∠AHC=45°.
(2)【解】S△BDM-S△ADN的值不发生改变.
如图②,连接OD.
∵BO⊥AC,OA=OB,∴∠BOA=90°,
∠BAO=∠ABO=45°.
∵D为AB的中点,∴∠DOA=45°.
∴∠DOM=90°+45°=135°,∠DAN=135°,∠ADO=90°,
∴∠DAN=∠DOM.∵MD⊥ND,∴∠MDN=90°.
∴∠NDA=90°-∠MDA=∠MDO.
在△ODM和△ADN中,
∴△ODM≌△ADN(ASA),∴S△ODM=S△ADN,
∴S△BDM-S△ADN=S△BDM-S△ODM=S△BOD=S△AOB=×AO·BO=××3×3=.
同课章节目录
