鲁教版(五四学制)数学七年级下册第七章 二元一次方程组 综合素质评价(含解析)
文档属性
| 名称 | 鲁教版(五四学制)数学七年级下册第七章 二元一次方程组 综合素质评价(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 00:00:00 | ||
图片预览




文档简介
第七章综合素质评价
一、选择题(每题3分,共36分)
1.下列方程中,是二元一次方程的是( )
A.2x+1=0 B.3x+y=2z C.xy=9 D.3x-2y=5
2.下列方程组:①②③④⑤其中是二元一次方程组的有( )
A.1个 B.2个 C.3个 D.4个
3.已知二元一次方程组用加减消元法解方程组正确的是( )
A.①×5-②×7 B.①×2+②×3
C.①×3-②×2 D.①×7-②×5
4.二元一次方程2x+y=5的非负整数解的个数是( )
A.1个 B.2个 C.3个 D.4个
5.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.- B. C. D.-
6.在同一平面直角坐标系中,一次函数 y1=kx-2(k为常数,k≠0)和y2=x+1的图象在第一象限相交于点P,点P的横坐标是2,则方程组的解是( )
A. B. C. D.
7.已知 x,y满足方程组则x+y的值为( )
A.-2 B.2 C.- D.
8.【2022·成都】中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )
A. B.
C. D.
9.定义运算“*”,规定x*y=ax2+by,其中a,b为常数,且1*2=5,2*1=6,则2*3=( )
A.8 B.9 C.10 D.12
10.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g
B.15 g,35 g
C.20 g,30 g
D.30 g,20 g
11.学校计划购买A,B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1 500元钱全部用于购买这两种品牌的足球(两种品牌的足球都购买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
12.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快递,乙仓库用来派发快递,该时段内甲、乙两仓库的快递数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(每题3分,共18分)
13.关于x,y的二元一次方程组的解是 则m+n的值为________.
14.以二元一次方程组的解为坐标的点(x,y)在第______象限.
15.关于x,y的两个二元一次方程组与的解相同,则 m+n=________.
16.一个三位数的各位数字之和等于14,个位数字与十位数字的和比百位数字大2,如果把百位数字与十位数字对调,所得新数比原数小270,则原三位数为________.
17.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将剩下的部分沿虚线剪开拼成一个长方形,如图②所示,拼成的这个长方形的长为30,宽为20,则图②中Ⅱ部分的面积是________.
18.若以关于x,y的二元一次方程组的解为坐标的点在一次函数y= -x+4的图象上,则k的值为________.
三、解答题(19~22题每题8分,23,24题每题10分,25题14分,共66分)
19.解方程组:
(1) (2)
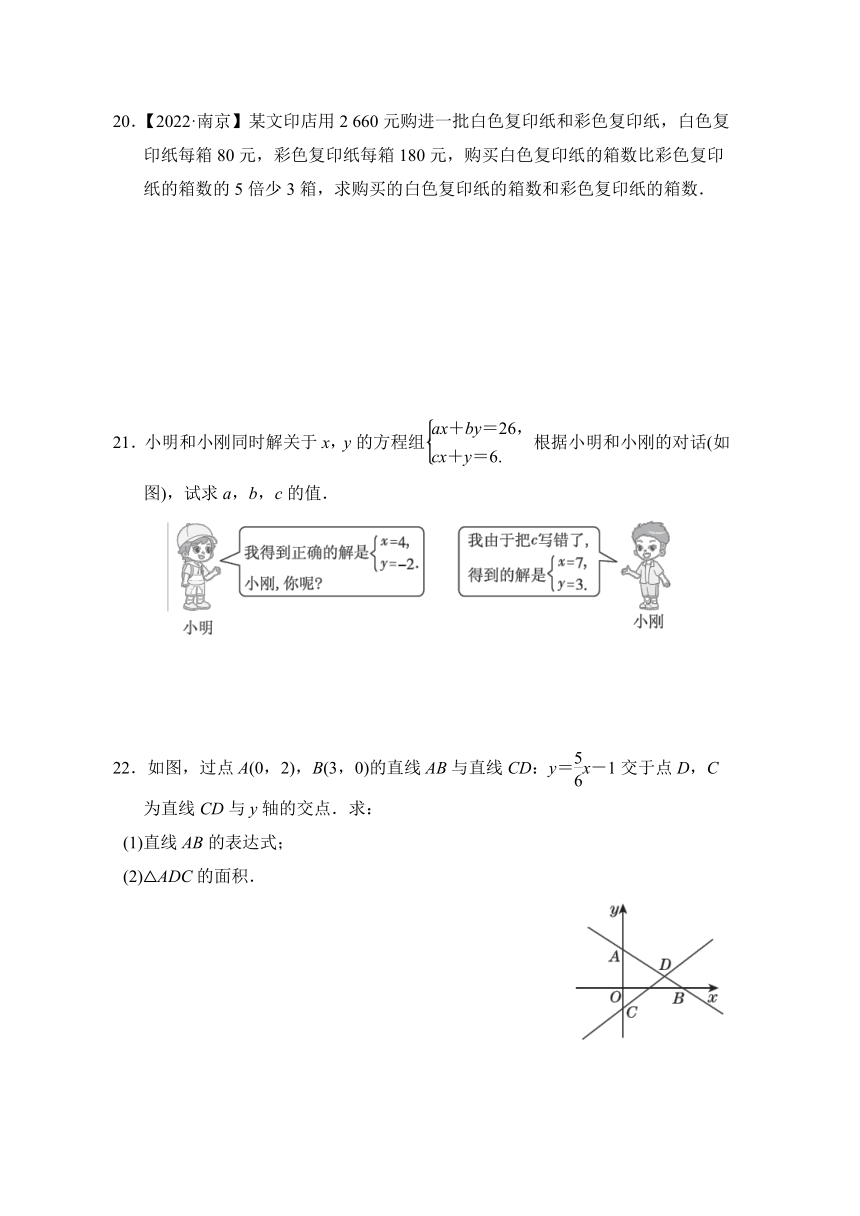
20.【2022·南京】某文印店用2 660元购进一批白色复印纸和彩色复印纸,白色复印纸每箱80元,彩色复印纸每箱180元,购买白色复印纸的箱数比彩色复印纸的箱数的5倍少3箱,求购买的白色复印纸的箱数和彩色复印纸的箱数.
21.小明和小刚同时解关于x,y的方程组根据小明和小刚的对话(如图),试求a,b,c的值.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x-1交于点D,C为直线CD与y轴的交点.求:
(1)直线AB的表达式;
(2)△ADC的面积.
23.【2023·张家界】为拓展学生视野,某中学组织八年级师生开展研学活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出三辆车,且其余客车恰好坐满.现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人/辆) 45 60
租金(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
24.已知A,B两地相距480 km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙两人离开A地的路程y(km)与时间x(h)的函数关系如图所示.
(1)分别求出甲、乙两人离开A地的路程y(km)与时间x(h)的函数表达式及相应自变量的取值范围;
(2)甲出发多长时间,两人相距20 km
25.【新考法】【2023·青岛即墨区期末】规定:形如关于x,y的方程x+ky=b与kx+y=b的两个方程互为共轭二元一次方程,其中k≠1,由这两个方程组成的方程组叫做共轭方程组.
(1)方程3x+y=5的共轭二元一次方程是____________.
(2)若关于x,y 的方程组为共轭方程组,求a,b的值.
(3)若方程x+ky=b中 x,y 的值满足下表:
x -1 0
y 0 2
求这个方程的共轭二元一次方程.
(4)解下列方程组(直接写出方程组的解):
的解为________;的解为________;
的解为____________.
答案
一、1.D 2.B 3.C
4.C 【点拨】因为2x+y=5,所以x=.
因为x,y都是非负整数,所以5-y=0或5-y=2或5-y=4.
当5-y=0时,y=5,x=0,所以
当5-y=2时,y=3,x=1,所以
当5-y=4时,y=1,x=2,所以
所以二元一次方程2x+y=5的非负整数解的个数是3个.
5.B 【点拨】
①+②,得2x=14k,解得x=7k,
①-②,得2y=-4k,解得y=-2k,
所以方程组的解为
将代入2x+3y=6,
得14k-6k=6,解得k=.
6.B
7.A 【点拨】
①+②,得6x+6y=-12,所以x+y=-2.
8.A 9.C 10.C 11.B 12.B
二、13.0 【点拨】将代入原方程组得解得
所以m+n=-2+2=0.
14.一 15.0
16.635 【点拨】设原三位数的个位、十位、百位上的数字分别为x,y,z,
则
解得 故原三位数为635.
17.100
18. 【点拨】
①+②,得2x=5+9k,所以x=;
①-②,得2y=5-9k,所以y=.把x=,y=代入y=-x+4,得=-×+4,解得k=.
三、19. 【解】(1)②×6,得3(x+y)-(x-y)=6,③
①-③,得-3(x-y)=0,所以x-y=0,即x=y.
将x=y代入③,得3(y+y)-0=6,解得y=1.所以x=1.
所以原方程组的解为
(2)②-①,得3x+3y=0,即x=-y,
③-①,得24x+6y=60,即4x+y=10,④
将x=-y代入④,得-4y+y=10,
解得y=-.所以x=.
将x=,y=-代入①,得z=-.
所以原方程组的解为
20.【解】设购买的白色复印纸有x箱,彩色复印纸有y箱.
由题意得
解得
答:购买的白色复印纸有22箱,彩色复印纸有5箱.
21.【解】把分别代入方程ax+by=26,得解得
把代入方程cx+y=6,
得4c+(-2)=6,解得c=2.
所以a=5,b=-3,c=2.
22.【解】(1)设直线AB的表达式为 y=kx+b,
把A(0,2),B(3,0)的坐标分别代入,
得解得
所以直线AB的表达式为 y=-x+2.
(2)当x=0时,y=x-1=-1,
所以点C的坐标为(0,-1).
解方程组得
所以点D的坐标为.
所以△ADC的面积为×(2+1)×2=3.
23.【解】(1)设参加此次研学活动的师生人数是x人,原计划租用y辆45座客车.
根据题意,得解得
答:参加此次研学活动的师生人数是600人,原计划租用13辆45座客车.
(2)租45座客车:600÷45≈14(辆),
所以需租14辆,租金为200×14=2 800(元),
租60座客车:600÷60=10(辆),
所以需租10辆,租金为300×10=3 000(元).
因为2 800<3 000,所以租用14辆45座客车更合算.
24.【解】(1)设甲离开A地的路程 y(km)与时间x(h)的函数表达式为y甲=mx,
把(6,480)代入,得 6m=480,
解得m=80,所以y甲=80x(0≤x≤6).
设乙离开A地的路程y(km)与时间x(h)的函数表达式为y乙=kx+b,
把(0.5,0),(4.5,480)分别代入,
得解得
所以y乙=120x-60(0.5≤x≤4.5).
(2)甲、乙两人相遇时,则80x=120x-60,解得x=1.5.
①乙出发前,即当0≤x<0.5时,
80x=20,解得x=;
②乙出发后还未追上甲,即当0.5≤x<1.5时,80x-(120x-60)=20,解得x=1;
③乙追上甲但还未到B地,即当1.5≤x<4.5时,(120x-60)-80x=20,解得 x=2;
④乙到B地后,即当4.5≤x≤6时,480-80x=20,解得x=.
综上所述,甲出发 h或1 h或 2 h或 h,两人相距20 km.
25.【解】(1)x+3y=5
(2)由题意得1-a=2a-2,b+2=4-b,
解得a=1,b=1.
(3)由题意得解得
所以原方程为x-0.5y=-1,
所以这个方程的共轭二元一次方程是-0.5x+y=-1.
(4)
一、选择题(每题3分,共36分)
1.下列方程中,是二元一次方程的是( )
A.2x+1=0 B.3x+y=2z C.xy=9 D.3x-2y=5
2.下列方程组:①②③④⑤其中是二元一次方程组的有( )
A.1个 B.2个 C.3个 D.4个
3.已知二元一次方程组用加减消元法解方程组正确的是( )
A.①×5-②×7 B.①×2+②×3
C.①×3-②×2 D.①×7-②×5
4.二元一次方程2x+y=5的非负整数解的个数是( )
A.1个 B.2个 C.3个 D.4个
5.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.- B. C. D.-
6.在同一平面直角坐标系中,一次函数 y1=kx-2(k为常数,k≠0)和y2=x+1的图象在第一象限相交于点P,点P的横坐标是2,则方程组的解是( )
A. B. C. D.
7.已知 x,y满足方程组则x+y的值为( )
A.-2 B.2 C.- D.
8.【2022·成都】中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )
A. B.
C. D.
9.定义运算“*”,规定x*y=ax2+by,其中a,b为常数,且1*2=5,2*1=6,则2*3=( )
A.8 B.9 C.10 D.12
10.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g
B.15 g,35 g
C.20 g,30 g
D.30 g,20 g
11.学校计划购买A,B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1 500元钱全部用于购买这两种品牌的足球(两种品牌的足球都购买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
12.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快递,乙仓库用来派发快递,该时段内甲、乙两仓库的快递数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(每题3分,共18分)
13.关于x,y的二元一次方程组的解是 则m+n的值为________.
14.以二元一次方程组的解为坐标的点(x,y)在第______象限.
15.关于x,y的两个二元一次方程组与的解相同,则 m+n=________.
16.一个三位数的各位数字之和等于14,个位数字与十位数字的和比百位数字大2,如果把百位数字与十位数字对调,所得新数比原数小270,则原三位数为________.
17.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将剩下的部分沿虚线剪开拼成一个长方形,如图②所示,拼成的这个长方形的长为30,宽为20,则图②中Ⅱ部分的面积是________.
18.若以关于x,y的二元一次方程组的解为坐标的点在一次函数y= -x+4的图象上,则k的值为________.
三、解答题(19~22题每题8分,23,24题每题10分,25题14分,共66分)
19.解方程组:
(1) (2)
20.【2022·南京】某文印店用2 660元购进一批白色复印纸和彩色复印纸,白色复印纸每箱80元,彩色复印纸每箱180元,购买白色复印纸的箱数比彩色复印纸的箱数的5倍少3箱,求购买的白色复印纸的箱数和彩色复印纸的箱数.
21.小明和小刚同时解关于x,y的方程组根据小明和小刚的对话(如图),试求a,b,c的值.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x-1交于点D,C为直线CD与y轴的交点.求:
(1)直线AB的表达式;
(2)△ADC的面积.
23.【2023·张家界】为拓展学生视野,某中学组织八年级师生开展研学活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出三辆车,且其余客车恰好坐满.现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人/辆) 45 60
租金(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
24.已知A,B两地相距480 km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙两人离开A地的路程y(km)与时间x(h)的函数关系如图所示.
(1)分别求出甲、乙两人离开A地的路程y(km)与时间x(h)的函数表达式及相应自变量的取值范围;
(2)甲出发多长时间,两人相距20 km
25.【新考法】【2023·青岛即墨区期末】规定:形如关于x,y的方程x+ky=b与kx+y=b的两个方程互为共轭二元一次方程,其中k≠1,由这两个方程组成的方程组叫做共轭方程组.
(1)方程3x+y=5的共轭二元一次方程是____________.
(2)若关于x,y 的方程组为共轭方程组,求a,b的值.
(3)若方程x+ky=b中 x,y 的值满足下表:
x -1 0
y 0 2
求这个方程的共轭二元一次方程.
(4)解下列方程组(直接写出方程组的解):
的解为________;的解为________;
的解为____________.
答案
一、1.D 2.B 3.C
4.C 【点拨】因为2x+y=5,所以x=.
因为x,y都是非负整数,所以5-y=0或5-y=2或5-y=4.
当5-y=0时,y=5,x=0,所以
当5-y=2时,y=3,x=1,所以
当5-y=4时,y=1,x=2,所以
所以二元一次方程2x+y=5的非负整数解的个数是3个.
5.B 【点拨】
①+②,得2x=14k,解得x=7k,
①-②,得2y=-4k,解得y=-2k,
所以方程组的解为
将代入2x+3y=6,
得14k-6k=6,解得k=.
6.B
7.A 【点拨】
①+②,得6x+6y=-12,所以x+y=-2.
8.A 9.C 10.C 11.B 12.B
二、13.0 【点拨】将代入原方程组得解得
所以m+n=-2+2=0.
14.一 15.0
16.635 【点拨】设原三位数的个位、十位、百位上的数字分别为x,y,z,
则
解得 故原三位数为635.
17.100
18. 【点拨】
①+②,得2x=5+9k,所以x=;
①-②,得2y=5-9k,所以y=.把x=,y=代入y=-x+4,得=-×+4,解得k=.
三、19. 【解】(1)②×6,得3(x+y)-(x-y)=6,③
①-③,得-3(x-y)=0,所以x-y=0,即x=y.
将x=y代入③,得3(y+y)-0=6,解得y=1.所以x=1.
所以原方程组的解为
(2)②-①,得3x+3y=0,即x=-y,
③-①,得24x+6y=60,即4x+y=10,④
将x=-y代入④,得-4y+y=10,
解得y=-.所以x=.
将x=,y=-代入①,得z=-.
所以原方程组的解为
20.【解】设购买的白色复印纸有x箱,彩色复印纸有y箱.
由题意得
解得
答:购买的白色复印纸有22箱,彩色复印纸有5箱.
21.【解】把分别代入方程ax+by=26,得解得
把代入方程cx+y=6,
得4c+(-2)=6,解得c=2.
所以a=5,b=-3,c=2.
22.【解】(1)设直线AB的表达式为 y=kx+b,
把A(0,2),B(3,0)的坐标分别代入,
得解得
所以直线AB的表达式为 y=-x+2.
(2)当x=0时,y=x-1=-1,
所以点C的坐标为(0,-1).
解方程组得
所以点D的坐标为.
所以△ADC的面积为×(2+1)×2=3.
23.【解】(1)设参加此次研学活动的师生人数是x人,原计划租用y辆45座客车.
根据题意,得解得
答:参加此次研学活动的师生人数是600人,原计划租用13辆45座客车.
(2)租45座客车:600÷45≈14(辆),
所以需租14辆,租金为200×14=2 800(元),
租60座客车:600÷60=10(辆),
所以需租10辆,租金为300×10=3 000(元).
因为2 800<3 000,所以租用14辆45座客车更合算.
24.【解】(1)设甲离开A地的路程 y(km)与时间x(h)的函数表达式为y甲=mx,
把(6,480)代入,得 6m=480,
解得m=80,所以y甲=80x(0≤x≤6).
设乙离开A地的路程y(km)与时间x(h)的函数表达式为y乙=kx+b,
把(0.5,0),(4.5,480)分别代入,
得解得
所以y乙=120x-60(0.5≤x≤4.5).
(2)甲、乙两人相遇时,则80x=120x-60,解得x=1.5.
①乙出发前,即当0≤x<0.5时,
80x=20,解得x=;
②乙出发后还未追上甲,即当0.5≤x<1.5时,80x-(120x-60)=20,解得x=1;
③乙追上甲但还未到B地,即当1.5≤x<4.5时,(120x-60)-80x=20,解得 x=2;
④乙到B地后,即当4.5≤x≤6时,480-80x=20,解得x=.
综上所述,甲出发 h或1 h或 2 h或 h,两人相距20 km.
25.【解】(1)x+3y=5
(2)由题意得1-a=2a-2,b+2=4-b,
解得a=1,b=1.
(3)由题意得解得
所以原方程为x-0.5y=-1,
所以这个方程的共轭二元一次方程是-0.5x+y=-1.
(4)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
