江西省南昌市重点中学2023-2024学年高一上学期12月月考(二)数学试题(PDF含解析)
文档属性
| 名称 | 江西省南昌市重点中学2023-2024学年高一上学期12月月考(二)数学试题(PDF含解析) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 21:52:30 | ||
图片预览



文档简介
一、单选题(本大题共 8 小题,共 40 分。在每小题列出的选项中,选出符合题目的一项)
1.命题“ ≥ 1,lg ≥ 0”的否定为( )
A. ≤ 1,lg < 0 B. ≤ 1,lg < 0
C. ≥ 1,lg < 0 D. ≥ 1,lg < 0
2.已知集合 = { | 2 4 + 3 ≤ 0}, = { |log0.5(4 7) > 0}则 ∩ =( )
A. [1,3] B. ( 74 , 3] C. [1,2) D. (
7
4 , 2)
3.第 32 届奥运会男子举重 73 公斤级决赛中,石智勇以抓举 166 公斤,挺举 198 公斤,总成绩 364 公斤
的成绩,为中国举重队再添一金,创造新的世界纪录.根据组别划分的最大体重以及举重成绩来看,举重的
总质量与运动员的体重有一定的关系,如图为某体育赛事举重质量与运动员体重之间关系的折线图,下面
模型中,最能刻画运动员体重和举重质量之间的关系的是 ( )
A. = + ( > 0) B. = + ( > 0)
C. = 2 + ( > 0) D. = + ( > 0, > 0 且 ≠ 1)
4.已知函数 ( )是定义在 上的偶函数,则下列结论一定成立的是( )
A. ∈ , ( ) ( ) > 0 B. 0 ∈ , ( 0) ( 0) > 0
C. ∈ , ( ) ( ) ≥ 0 D. 0 ∈ , ( 0) ( 0) < 0
5.已知 = , = 52, =
1
2,则 , , 的大小关系为( )(课本 128 3)
A. > > B. > > C. > > D. > >
6.已知 ( )是定义在 上的奇函数, (3) = 3,对 1, 2 ∈ [0, + ∞)
· ( ) · ( )
,且 1 ≠ 2有
1 1 2 2
> 0,则1 2
关于 的不等式( + 2) ( + 2) < 9 的解集为 ( )
A. ( ∞,1) B. ( 5,1)
C. ( ∞, 5) ∪ (1, + ∞) D. ( ∞, 1) ∪ (1, + ∞)
第 1页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
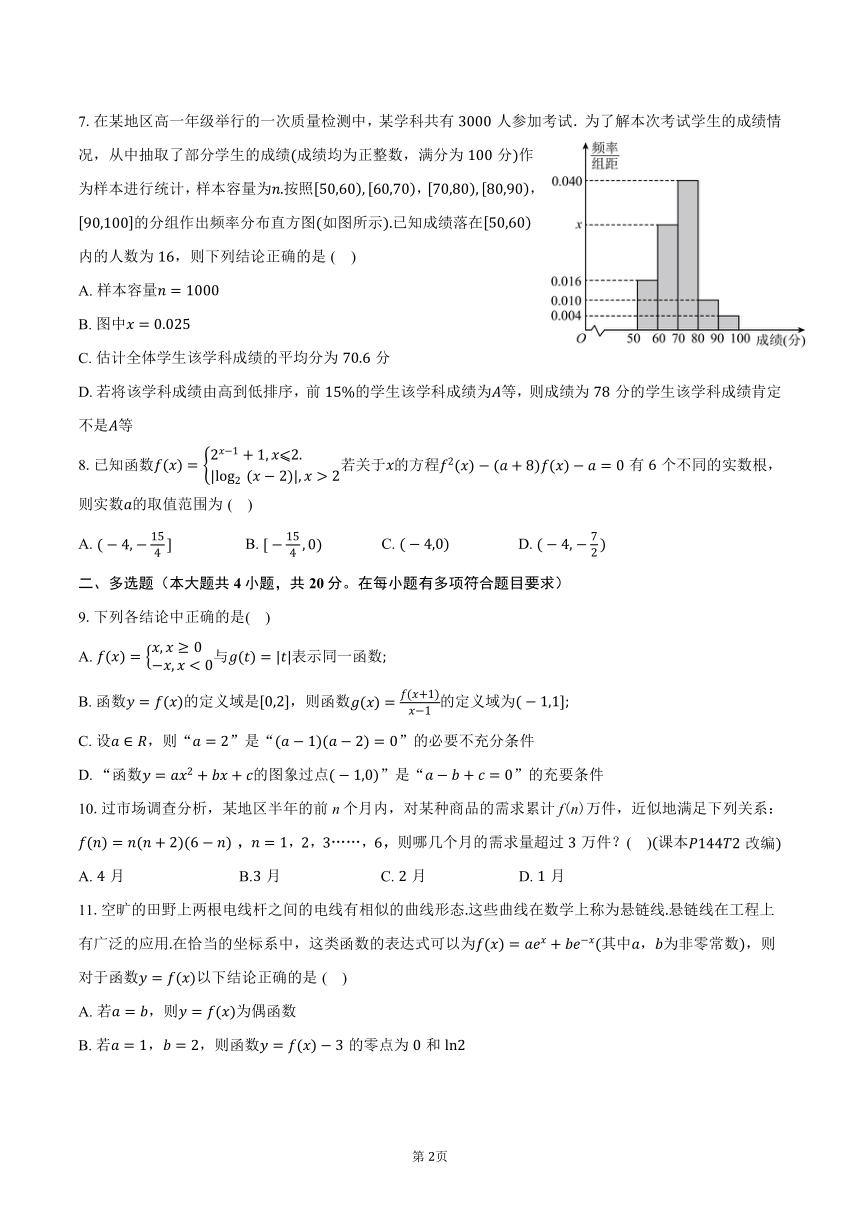
7.在某地区高一年级举行的一次质量检测中,某学科共有 3000 人参加考试.为了解本次考试学生的成绩情
况,从中抽取了部分学生的成绩(成绩均为正整数,满分为 100 分)作
为样本进行统计,样本容量为 .按照 50,60 , 60,70 ,70,80 , 80,90 ,
90,100 的分组作出频率分布直方图(如图所示).已知成绩落在 50,60
内的人数为 16,则下列结论正确的是 ( )
A.样本容量 = 1000
B.图中 = 0.025
C.估计全体学生该学科成绩的平均分为 70.6 分
D.若将该学科成绩由高到低排序,前 15%的学生该学科成绩为 等,则成绩为 78 分的学生该学科成绩肯定
不是 等
2 1 + 1, 2.
8.已知函数 ( ) = 若关于 的方程 2( ) ( + 8) ( ) = 0 有 6 个不同的实数根,
|log2 ( 2)|, > 2
则实数 的取值范围为 ( )
A. ( 4, 154 ] B. [
15
4 , 0) C. ( 4,0) D. ( 4,
7
2 )
二、多选题(本大题共 4 小题,共 20 分。在每小题有多项符合题目要求)
9.下列各结论中正确的是( )
A. ( ) = , ≥ 0 , < 0与 ( ) = | |表示同一函数;
B.函数 = ( ) ( +1)的定义域是[0,2],则函数 ( ) = 1 的定义域为( 1,1];
C.设 ∈ ,则“ = 2”是“( 1)( 2) = 0”的必要不充分条件
D.“函数 = 2 + + 的图象过点( 1,0)”是“ + = 0”的充要条件
10.过市场调查分析,某地区半年的前 n 个月内,对某种商品的需求累计 f(n)万件,近似地满足下列关系:
( ) = ( + 2)(6 ) , = 1,2,3……,6,则哪几个月的需求量超过 3 万件?( )(课本 144 2 改编)
A. 4 月 B.3 月 C. 2 月 D. 1 月
11.空旷的田野上两根电线杆之间的电线有相似的曲线形态.这些曲线在数学上称为悬链线.悬链线在工程上
有广泛的应用.在恰当的坐标系中,这类函数的表达式可以为 ( ) = + (其中 , 为非零常数),则
对于函数 = ( )以下结论正确的是 ( )
A.若 = ,则 = ( )为偶函数
B.若 = 1, = 2,则函数 = ( ) 3 的零点为 0 和 ln2
第 2页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
C.若 = 1,则函数 = ( )的最小值为 2
D.若 = ( )为奇函数,且 ∈ ( ∞,0)使 2 + 2 + ( ) ≤ 0 成立,则 的最小值为 2 2
经
2022 2023
12.设 = 2 +1 = 2 +12023 , 2024 ,则下列说法中正确的是 ( )2 +1 2 +1
A. > B. 2 < 2
C. 12 <
2 + 2 < 2 D. + 的最小值为 2
三、填空题(本大题共 4 小题,共 20 分)
13.若 > > 1,则函数 = log + 的图像不经过第________象限. (课本 127 11(1))
14 > 0 > 0 +1 3.已知 , ,且 + = 2,则 3 + 的最小值为_________.
415 ( ) = 2
2+9
.已知 22 , ( ) = + 9.若对 2 ∈ [2,3],总存在 1 ∈ [1,2]使得 ( 2) > ( 1)成立,则
实数 的取值范围为_________.
9, <
16.若函数 ( ) = 8 ( 3)2, ≥ 存在最大值,则实数 的取值范围为_________.
四、解答题(本大题共 6 小题,共 70 分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题 10 分)(1)计算:23+log25 + (log43 + log83)·(log32 + log92)的值;(课本 108 5(2) + 107 6(6))
1 1
2 2
(2)已知 + = 12, = 9 ,且 > ,求 1 1的值. (课本 95 1)
2+ 2
18.( 1 1本小题 12 分)已知函数 ( ) = 2 +1 2 . (课本 94 8 改编)
(1)判断函数 ( )的奇偶性,并说明理由;
(2)解不等式 ( 2 2 ) + 2 2 1 < 0.
19.(本小题 12 分)南昌的西瓜脆甜爽口,汁多肉厚,其实在南昌还有一种香瓜也非常好吃,由于个小产量
也少,往往供不应求,所以不被大家熟悉.南昌某种植园在香
瓜成熟时,随机从一些香瓜藤上摘下 100 个香瓜,称得其质量
分别在[150,250),[250,350),[350,450),[450,550),
[550,650)(单位:克)中,经统计绘制频率分布直方图如图所示:
(1)在样本中,按分层抽样从质量在[250,450)中的香瓜中随机
抽取了 个香瓜,其中质量在[250,350)中的香瓜有 6 个,求
的值;
(2)估计这组数据的平均数(同一组中的数据以这组数据所在区
第 3页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
间的中点值作代表);
(3)某个体经销商来收购香瓜,同一组中的数据以这组数据所在区间的中点值作代表,用样本估计总体,该
种植园中大概共有香瓜 2 万个,经销商提出以下两种收购方案:方案①:所有香瓜以 5 元/500 克收购;方
案②:对质量低于 350 克的香瓜以 3 元/个收购,对质量高于或等于 350 克的香瓜以 5 元/个收购.请分别
计算两种方案获得的利润,并说明种植园选择哪种方案获利更多?
20.(本小题 12 分)习近平指出,倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态
环保思想成为社会生话中的主流文化.某化工企业探索改良工艺,使排放的废气中含有的污染物数量逐渐
减少.已知改良工艺前所排放的废气中含有的污染物数量为 2 / 3,首次改良后所排放的废气中含有的
污染数量为 1.94 / 3.设改良工艺前所排放的废气中含有的污染物数量为 0,首次改良工艺后所排放的废
气中含有的污染物数量为 1,则第 次改良后所排放的废气中的污染物数量 ,可由函数模型 = 0 ( 0
1)·50.5 + ( ∈ , ∈ )给出,其中 是指改良工艺的次数.
(1)试求改良后 的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过 0.08 / 3.试问:至少进行多少
次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标?(参考数据:取 lg 2 = 0.3)
21.(本小题 12 分)如果函数 = ( )的定义域为 ,且存在实常数 ,使得对定义域内的任意 ,都有 ( +
) = ( )恒成立,那么称此函数具有“ ( )性质”.
(1)已知 = ( )具有“ (0)性质”,且当 ≤ 0 时, ( ) = ( + )2,求 = ( )在[0,1]的最大值;
(2)已知定义在 上的函数 = ( )具有“ (2)性质”,当 ≥ 1 时, ( ) = | 4|.若函数 = 2
· + 有 8 个零点,求实数 的取值范围.
22.( 1本小题 12 分)已知函数 ( ) = ( 2 )
,函数 ( )图象与 ( )的图象关于 = 对称.
(1)若函数 = 2 2 + 1 在(1, + ∞)上单调递减,求实数 的取值范围;
(2)不等式 ( 2 ) < 2 ( + 2 6)在 ∈ [4,9]上恒成立,求实数 的取值范围.
第 4页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D A C B B C A AD BCD ABD AC
13.四 14.12 15. ∞,2 5 16. 0 ≤ ≤ 4
1.【答案】 2.【答案】 3.【答案】A4.【答案】 5.【答案】B
6.【答案】 解:因为 ( )是定义在 上的奇函数,则 ( ) = ( )是定义在 上的偶函数,且 ( )在[0, + ∞)
上单调递增, (3) = 3,所以 ( )在[0, + ∞)上单调递增,在( ∞,0]上单调递减, (3) = 3 (3) = 9,
( + 2) ( + 2) < 9 ( + 2) < (3) + 2 < 3,解得: 5 < < 1.
7.【答案】 解:对于 ,成绩落在[50,60)的频率为 0.016 × 10 = 0.16,
16
又∵成绩落在[50,60)内的人数为 16,∴ = 0.16 = 100,故 A 错误;
对于 ,由频率分布直方图可得,(0.016 + + 0.040 + 0.010 + 0.004) × 10 = 1,解得 = 0.030,故 B 错
误;
对于 ,估计全体学生该学科成绩的平均分为: = 55 × 0.16 + 65 × 0.3 + 75 × 0.4 + 85 × 0.1 + 95 ×
0.04 = 70.6(分),故 C 正确;
对于 ,∵ 10 × (0.004 + 0.010) = 0.14 < 0.15,10 × (0.004 + 0.010 + 0.040) = 0.56 > 0.15,∴ 等成绩的
最低分落在[70,80),
设该学科成绩为 等的最低分数为 ,则(80 ) × 0.04 + 0.1 + 0.04 = 0.15,解得 = 79.75,
虽然 79.75 > 78,但 79.75 是估计值,[70,80)是一个区间,有可能出现没有学生考到 79 分的情况(学生成
绩均为正整数),这种情况下成绩为 78 分的学生该学科成绩可以是 等, D 错误,故选: .
8.【答案】 解:作函数 ( )的图象如下:
由图象知:要关于 的方程 2( ) ( + 8) ( ) = 0 有 6
个不同的实数根,
设 ( ) = ,则关于 的方程 2 ( + 8) = 0 在 1,3 有两
个不同的实数根,
+ 8 2 4 × 1 × > 0
1 < +82 < 3 4 < ≤ 15 15因此 ,解得 4,所以实数 的取值范围为 4, .1 ( + 8) > 0 4
9 3 + 8 0
9.【答案】 , ≥ 0 , ≥ 0解:对于 , ( ) = , < 0, ( ) = = ( ) = , < 0,
因为 ( )与 ( )定义域,解析式一致,故 A 正确;
第 5页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
对于 , ( )分母不能为 0,所以 ≠ 1,又 0 ≤ + 1 ≤ 2,得 1 ≤ ≤ 1,
所以 ( )的定义域为[ 1,1)故 B 不正确;
对于 ,若( 1)( 2) = 0,则 = 1 或 = 2,
所以“ = 2”是“( 1)( 2) = 0”的的充分不必要条件,故 C 错误;
对于 ,若函数 = 2 + + 的图象过点( 1,0),则 + = 0,
若 + = 0,则当 = 1 时, = + = 0,即函数 = 2 + + 的图象过点( 1,0),
“函数 = 2 + + 的图象过点( 1,0)”是“ + = 0”的充要条件,故 D 正确.故选: .
10.【答案】B D 解: 1 = 15 > 3; ≥ 2 时, ( 1) = 3 2 + 11 + 7 > 3 得 < 4,
所以 = 1,2,3.
11.【答案】 解:若 = , = + ,则 ( ) = + = + ,
所以 ( ) = + = ( ),所以 ( )是偶函数,A 正确;
若 = 1, = 2, = + 2 3,由 + 2 3 = 0 得 = 0 或 2,
所以函数 = 3 的零点为 0 和 ln2,B 正确;
若 = 1,设 = = 1 时,显然 ( ) < 0,C 错误;
若 = 为奇函数,则 ( ) = ( )恒成立,即 + = ( + ),
整理得( + )( + ) = 0 恒成立,即 = ,所以 ( ) = ,
从而 2 + 2 + ≤ 0 可转化为 2 + 2 + 0,
令 = ,则 2 + 2 = ( )2 + 2 = 2 + 2,即 2 + + 2 ≤ 0,
其中当 ∈ ( ∞,0)时, =
2
∈ ( ∞,0),所以 ≥ 2 =
2 ,
显然 = 2 = +
2
≥ 2 2,所以 的最小值为 2 2,D 正确.故选 ABD.
1 +1 1 1
12.【答案】 解:构造函数 = 2 +1 +1 ,则 = 2
(2 +1)+2
2 +1 2 +1+1 =
1
2 +
2 ,
2 +1+1
1
因为函数 = 2 +1在 上为单调递增函数,则 = 2 在 上为单调递减函数,2 +1+1
所以 ( )在 上为单调递减函数,所以 (2022) > (2023) > 0,即 > ,2 > 2 ,故选项 A 正确,选项 B
; 1 2
2022+1 1 22023+1 1
错误 因为 < = 2023 < 1, < = 2024 < 1,所以2 <
2 + 2 < 2,故选项 C 正确;
2 2 +1 2 2 +1
因为
+ ≥ 2 · = 2,当且仅当 = 时取等号,由题意可知 ≠ ,故 + ≠ 2,故选项 D 错误.故选 AC.
13.【答案】四
第 6页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
14. 1 3【答案】12 解:因为 > 0, > 0,且 + = 1,
所以 3 + = (3 + )( 1 3 + ) = 3 + 3 +
9
+ ≥ 6+ 2
9
· = 6 + 2 × 3 = 12,
当且仅当 = 3 ,即 = 2, = 6 时取等号,此时 3 + 的最小值为 12.
4
∞,2 5 ( ) = 2
2+9 9
15.【答案】 解: 22 = + 2 2,当 ∈ [1,2]时,
2 ∈ [1,4],当 2 = 3 时, ( ) = 4,
对 2 ∈ [2,3],总存在 1 ∈ [1,2]使得 ( 2) > ( 1)成立,
即 ∈ [2,3] ( ) > ( ) = 4,即 ( ) = 2 + 9 > 4,
2 5
得 ∈ 2,3 , < +5 = +
5,当 = 5时, + = 2 5.综上可知,实数 的取值范围为 ∞,2 5 . min
16.【答案】 0 ≤ ≤ 4 解: ①当 < 0 时,函数 ( )在( ∞, )上单调递减,因此 ( )不存在最大值;
9, < 0
②当 = 0 时, ( ) = 8 ( 3)2, ≥ 0,当 ≥ 0 时, ( )max = (3) = 8 > 9,故函数 ( )存在最大
值;
③当 0 < < 3 时,故函数 ( )在( , 3)上单调递增,在(3, + ∞)上单调递减,故 ≥ 时, ( ) = 8 (
3)2 ≤ 8,
当 < 时,函数 ( )在( ∞, )上单调递增,此时 ( ) < ( ) = 2 9.于是 2 9 ≤ 8 时函数存在最大
值.解得 0 < < 3.
④当 3 时,函数在( , + ∞)上单调递减, ( ) ≤ ( ) = 8 ( 3)2.
在( ∞, )上单调递增,此时 ( ) < ( ) = 2 9.故当 8 ( 3)2 ≥ 2 9,解得 1 ≤ ≤ 4,故 3 4;
综上,0 ≤ ≤ 4 时函数 ( )存在最大值.
17.解:(1)23+log25 + (log43 + log83)·(log32 + log92) = 8 × 5 +
5
6 log 3 ·
3 5 165
2 2 log32 = 40 + 4 = 4 . ……5 分
(2)因为 + = 12, = 9,所以 2 = + 2 4 = 36 × 3,得 = 6 3;……7 分
1 1 1 1 1 1
2 2 2 2 2 2 2
所以 1 1 =
( )
=
+ 2 · = 12 2 9 6 3 =
3
3 . ……10 分 2+ 2
18. (1) ( ) ( ) + = 1 1
解: 的定义域为 ,且 2 +1 2 + +
1 1
2 +1 2 =
2 1
1+2 + 2 +1 1 =
1 1 = 0,所以 ( )为奇函数;……6 分
(2) ( )在 上是奇函数且是减函数,……8 分
由不等式 ( 2 2 ) + (2 2 1) < 0 得 ( 2 2 ) < (2 2 1) = 1 2 2 ;……9 分
所以 2 2 > 1 2 2,即得{ | < 13或 > 1}. ……12 分
第 7页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
19.解:(1) 6 0.2 2按分层抽样, = 0.2+0.3 = 5,所以 = 15; ……3 分
(2)由频率分布直方图知,各区间频率为 0.17,0.20,0.30,0.25,0.08,
这组数据的平均数: = 0.17 × 200 + 0.20 × 300 + 0.30 × 400 + 0.25 × 500 + 0.08 × 600 = 387;……6 分
(3)方案 ①:根据题意可知 20000 个香瓜中:
200 克的有 0.17 × 20000 = 3400 个,300 克的有:0.20 × 20000 = 4000 个,
400 克的有:0.30 × 20000 = 6000 个,500 克的有:0.25 × 20000 = 5000 个,
600 克的有:0.08 × 20000 = 1600 个,
3400×200+4000×300+6000×400+5000×500+1600×600
500 × 5 = 77400 元; ……9 分
方案 ②:质量低于 350 克的香瓜有(0.17 + 0.20) × 20000 = 7400 个,
质量高于或等于 350 克的香瓜有 20000 7400 = 12600 个,
7400 × 3 + 12600 × 5 = 85200 元,且 85200 > 77400,……11 分
综上,种植园选择方案 ②获利更多. ……12 分
20.解:(1)由题意得 0 = 2, 1 = 1.94,所以当 = 1 时, 1 = 0 ( 0 1) 50.5+ ,
即 1.94 = 2 (2 1.94) 50.5+ ,解得 = 0.5,……3 分
所以 0.5 0.5 = 2 0.06 × 5 ∈ ,
故改良后所排放的废气中含有的污染物数量的函数模型为 = 2 0.06 × 50.5 0.5 ∈ . ……5 分
(2)由题意可得 = 2 0.06 × 50.5 0.5 ≤ 0.08,整理得50.5 0.5 ≥ 32,……6 分
两边同时取常用对数,得 0.5 0.5 ≥ lg32 5lg2lg5,整理得 ≥ 2 × 1 lg2 + 1,……9 分
2 = 0.3 2 × 5lg2 + 1 = 30将 代入,可得 1 lg2 7 + 1 ≈ 5.3,所以 ≥ 5.3,……11 分
又因为 ∈ ,所以 ≥ 6,
综上,至少进行 6 次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.……12 分
21.【答案】解:(1) ∵ = ( )具有“ (0)性质”∴ ( ) = ( )对 ∈ 恒成立∴ ( )是偶函数,……1 分
∴当 ∈ [0,1]时, ( ) = ( + )2 = ( )2,……3 分
∴当 ≤ 12时, ( ) = (1) = (1 )
2; ……5 分
1
当 > 2时, ( ) = (0) =
2. ……6 分
(2)函数 = ( )具有“性质 (2),则 ( + 2) = ( ),
当 ≥ 1 时, ( ) = | 4|,所以当 < 1 时,
第 8页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
| 4|, ≥ 1
( ) = ( + 2) = | + 2|,于是 ( ) = | + 2|, < 1 . ……8 分
函数 = 2 · + 有 8 个零点,令 = ( ),
则 2 + = 0 有两个不等的实数根 1, 2,且 0 < 1 < 3,0 < 2 < 3,……9 分
= 2 4 > 0
> 0
{ 9 9所以 32 3 + > 0,所以 4 < < 2 .所以 的取值范围为(4, 2 ). ……12 分
0 < 2 < 3
22.【答案】解:依题意 ( ) = log1 ,……1 分
2
(1) = 2 2 + 1 = log1( 2 2 + 1)在(1, + ∞)上单调递减,
2
令 ( ) = 2 2 + 1,则 ( )在(1, + ∞)上单调递增,且 ( ) > 0 对 ∈ (1, + ∞)恒成立.……3 分
∴ ≤ 1,且 (1) = 1 2 + 1 ≥ 0,∴ ≤ 1.故 的取值范围为( ∞,1].……5 分
(2)依题意有 2 > 0,且 4 + 2 6 > 0,∴ > 1. ……6 分
不等式log1( 2 ) < 2log1( + 2 6)在[4,9]上恒成立,
2 2
即 2 > ( + 2 6)2在[4,9]上恒成立,……7分
∴ > + 2 6,∴ ( 2) > 6 在[4,9]上恒成立,
当 = 4 6 6时不等式成立,所以必须 > 2在(4,9]上恒成立∴ > ( 2 )max……9分
6 2 2 = ∈ (0,1] = +4 2 = 2 2令 , , ,而 2 + 4 + 4 在(0,1]上单调递增,
∴ ( 2 + 4)max = 3,∴ > 3
综上: 的取值范围为(3, + ∞).……12分
第 9页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
1.命题“ ≥ 1,lg ≥ 0”的否定为( )
A. ≤ 1,lg < 0 B. ≤ 1,lg < 0
C. ≥ 1,lg < 0 D. ≥ 1,lg < 0
2.已知集合 = { | 2 4 + 3 ≤ 0}, = { |log0.5(4 7) > 0}则 ∩ =( )
A. [1,3] B. ( 74 , 3] C. [1,2) D. (
7
4 , 2)
3.第 32 届奥运会男子举重 73 公斤级决赛中,石智勇以抓举 166 公斤,挺举 198 公斤,总成绩 364 公斤
的成绩,为中国举重队再添一金,创造新的世界纪录.根据组别划分的最大体重以及举重成绩来看,举重的
总质量与运动员的体重有一定的关系,如图为某体育赛事举重质量与运动员体重之间关系的折线图,下面
模型中,最能刻画运动员体重和举重质量之间的关系的是 ( )
A. = + ( > 0) B. = + ( > 0)
C. = 2 + ( > 0) D. = + ( > 0, > 0 且 ≠ 1)
4.已知函数 ( )是定义在 上的偶函数,则下列结论一定成立的是( )
A. ∈ , ( ) ( ) > 0 B. 0 ∈ , ( 0) ( 0) > 0
C. ∈ , ( ) ( ) ≥ 0 D. 0 ∈ , ( 0) ( 0) < 0
5.已知 = , = 52, =
1
2,则 , , 的大小关系为( )(课本 128 3)
A. > > B. > > C. > > D. > >
6.已知 ( )是定义在 上的奇函数, (3) = 3,对 1, 2 ∈ [0, + ∞)
· ( ) · ( )
,且 1 ≠ 2有
1 1 2 2
> 0,则1 2
关于 的不等式( + 2) ( + 2) < 9 的解集为 ( )
A. ( ∞,1) B. ( 5,1)
C. ( ∞, 5) ∪ (1, + ∞) D. ( ∞, 1) ∪ (1, + ∞)
第 1页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
7.在某地区高一年级举行的一次质量检测中,某学科共有 3000 人参加考试.为了解本次考试学生的成绩情
况,从中抽取了部分学生的成绩(成绩均为正整数,满分为 100 分)作
为样本进行统计,样本容量为 .按照 50,60 , 60,70 ,70,80 , 80,90 ,
90,100 的分组作出频率分布直方图(如图所示).已知成绩落在 50,60
内的人数为 16,则下列结论正确的是 ( )
A.样本容量 = 1000
B.图中 = 0.025
C.估计全体学生该学科成绩的平均分为 70.6 分
D.若将该学科成绩由高到低排序,前 15%的学生该学科成绩为 等,则成绩为 78 分的学生该学科成绩肯定
不是 等
2 1 + 1, 2.
8.已知函数 ( ) = 若关于 的方程 2( ) ( + 8) ( ) = 0 有 6 个不同的实数根,
|log2 ( 2)|, > 2
则实数 的取值范围为 ( )
A. ( 4, 154 ] B. [
15
4 , 0) C. ( 4,0) D. ( 4,
7
2 )
二、多选题(本大题共 4 小题,共 20 分。在每小题有多项符合题目要求)
9.下列各结论中正确的是( )
A. ( ) = , ≥ 0 , < 0与 ( ) = | |表示同一函数;
B.函数 = ( ) ( +1)的定义域是[0,2],则函数 ( ) = 1 的定义域为( 1,1];
C.设 ∈ ,则“ = 2”是“( 1)( 2) = 0”的必要不充分条件
D.“函数 = 2 + + 的图象过点( 1,0)”是“ + = 0”的充要条件
10.过市场调查分析,某地区半年的前 n 个月内,对某种商品的需求累计 f(n)万件,近似地满足下列关系:
( ) = ( + 2)(6 ) , = 1,2,3……,6,则哪几个月的需求量超过 3 万件?( )(课本 144 2 改编)
A. 4 月 B.3 月 C. 2 月 D. 1 月
11.空旷的田野上两根电线杆之间的电线有相似的曲线形态.这些曲线在数学上称为悬链线.悬链线在工程上
有广泛的应用.在恰当的坐标系中,这类函数的表达式可以为 ( ) = + (其中 , 为非零常数),则
对于函数 = ( )以下结论正确的是 ( )
A.若 = ,则 = ( )为偶函数
B.若 = 1, = 2,则函数 = ( ) 3 的零点为 0 和 ln2
第 2页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
C.若 = 1,则函数 = ( )的最小值为 2
D.若 = ( )为奇函数,且 ∈ ( ∞,0)使 2 + 2 + ( ) ≤ 0 成立,则 的最小值为 2 2
经
2022 2023
12.设 = 2 +1 = 2 +12023 , 2024 ,则下列说法中正确的是 ( )2 +1 2 +1
A. > B. 2 < 2
C. 12 <
2 + 2 < 2 D. + 的最小值为 2
三、填空题(本大题共 4 小题,共 20 分)
13.若 > > 1,则函数 = log + 的图像不经过第________象限. (课本 127 11(1))
14 > 0 > 0 +1 3.已知 , ,且 + = 2,则 3 + 的最小值为_________.
415 ( ) = 2
2+9
.已知 22 , ( ) = + 9.若对 2 ∈ [2,3],总存在 1 ∈ [1,2]使得 ( 2) > ( 1)成立,则
实数 的取值范围为_________.
9, <
16.若函数 ( ) = 8 ( 3)2, ≥ 存在最大值,则实数 的取值范围为_________.
四、解答题(本大题共 6 小题,共 70 分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题 10 分)(1)计算:23+log25 + (log43 + log83)·(log32 + log92)的值;(课本 108 5(2) + 107 6(6))
1 1
2 2
(2)已知 + = 12, = 9 ,且 > ,求 1 1的值. (课本 95 1)
2+ 2
18.( 1 1本小题 12 分)已知函数 ( ) = 2 +1 2 . (课本 94 8 改编)
(1)判断函数 ( )的奇偶性,并说明理由;
(2)解不等式 ( 2 2 ) + 2 2 1 < 0.
19.(本小题 12 分)南昌的西瓜脆甜爽口,汁多肉厚,其实在南昌还有一种香瓜也非常好吃,由于个小产量
也少,往往供不应求,所以不被大家熟悉.南昌某种植园在香
瓜成熟时,随机从一些香瓜藤上摘下 100 个香瓜,称得其质量
分别在[150,250),[250,350),[350,450),[450,550),
[550,650)(单位:克)中,经统计绘制频率分布直方图如图所示:
(1)在样本中,按分层抽样从质量在[250,450)中的香瓜中随机
抽取了 个香瓜,其中质量在[250,350)中的香瓜有 6 个,求
的值;
(2)估计这组数据的平均数(同一组中的数据以这组数据所在区
第 3页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
间的中点值作代表);
(3)某个体经销商来收购香瓜,同一组中的数据以这组数据所在区间的中点值作代表,用样本估计总体,该
种植园中大概共有香瓜 2 万个,经销商提出以下两种收购方案:方案①:所有香瓜以 5 元/500 克收购;方
案②:对质量低于 350 克的香瓜以 3 元/个收购,对质量高于或等于 350 克的香瓜以 5 元/个收购.请分别
计算两种方案获得的利润,并说明种植园选择哪种方案获利更多?
20.(本小题 12 分)习近平指出,倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态
环保思想成为社会生话中的主流文化.某化工企业探索改良工艺,使排放的废气中含有的污染物数量逐渐
减少.已知改良工艺前所排放的废气中含有的污染物数量为 2 / 3,首次改良后所排放的废气中含有的
污染数量为 1.94 / 3.设改良工艺前所排放的废气中含有的污染物数量为 0,首次改良工艺后所排放的废
气中含有的污染物数量为 1,则第 次改良后所排放的废气中的污染物数量 ,可由函数模型 = 0 ( 0
1)·50.5 + ( ∈ , ∈ )给出,其中 是指改良工艺的次数.
(1)试求改良后 的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过 0.08 / 3.试问:至少进行多少
次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标?(参考数据:取 lg 2 = 0.3)
21.(本小题 12 分)如果函数 = ( )的定义域为 ,且存在实常数 ,使得对定义域内的任意 ,都有 ( +
) = ( )恒成立,那么称此函数具有“ ( )性质”.
(1)已知 = ( )具有“ (0)性质”,且当 ≤ 0 时, ( ) = ( + )2,求 = ( )在[0,1]的最大值;
(2)已知定义在 上的函数 = ( )具有“ (2)性质”,当 ≥ 1 时, ( ) = | 4|.若函数 = 2
· + 有 8 个零点,求实数 的取值范围.
22.( 1本小题 12 分)已知函数 ( ) = ( 2 )
,函数 ( )图象与 ( )的图象关于 = 对称.
(1)若函数 = 2 2 + 1 在(1, + ∞)上单调递减,求实数 的取值范围;
(2)不等式 ( 2 ) < 2 ( + 2 6)在 ∈ [4,9]上恒成立,求实数 的取值范围.
第 4页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D A C B B C A AD BCD ABD AC
13.四 14.12 15. ∞,2 5 16. 0 ≤ ≤ 4
1.【答案】 2.【答案】 3.【答案】A4.【答案】 5.【答案】B
6.【答案】 解:因为 ( )是定义在 上的奇函数,则 ( ) = ( )是定义在 上的偶函数,且 ( )在[0, + ∞)
上单调递增, (3) = 3,所以 ( )在[0, + ∞)上单调递增,在( ∞,0]上单调递减, (3) = 3 (3) = 9,
( + 2) ( + 2) < 9 ( + 2) < (3) + 2 < 3,解得: 5 < < 1.
7.【答案】 解:对于 ,成绩落在[50,60)的频率为 0.016 × 10 = 0.16,
16
又∵成绩落在[50,60)内的人数为 16,∴ = 0.16 = 100,故 A 错误;
对于 ,由频率分布直方图可得,(0.016 + + 0.040 + 0.010 + 0.004) × 10 = 1,解得 = 0.030,故 B 错
误;
对于 ,估计全体学生该学科成绩的平均分为: = 55 × 0.16 + 65 × 0.3 + 75 × 0.4 + 85 × 0.1 + 95 ×
0.04 = 70.6(分),故 C 正确;
对于 ,∵ 10 × (0.004 + 0.010) = 0.14 < 0.15,10 × (0.004 + 0.010 + 0.040) = 0.56 > 0.15,∴ 等成绩的
最低分落在[70,80),
设该学科成绩为 等的最低分数为 ,则(80 ) × 0.04 + 0.1 + 0.04 = 0.15,解得 = 79.75,
虽然 79.75 > 78,但 79.75 是估计值,[70,80)是一个区间,有可能出现没有学生考到 79 分的情况(学生成
绩均为正整数),这种情况下成绩为 78 分的学生该学科成绩可以是 等, D 错误,故选: .
8.【答案】 解:作函数 ( )的图象如下:
由图象知:要关于 的方程 2( ) ( + 8) ( ) = 0 有 6
个不同的实数根,
设 ( ) = ,则关于 的方程 2 ( + 8) = 0 在 1,3 有两
个不同的实数根,
+ 8 2 4 × 1 × > 0
1 < +82 < 3 4 < ≤ 15 15因此 ,解得 4,所以实数 的取值范围为 4, .1 ( + 8) > 0 4
9 3 + 8 0
9.【答案】 , ≥ 0 , ≥ 0解:对于 , ( ) = , < 0, ( ) = = ( ) = , < 0,
因为 ( )与 ( )定义域,解析式一致,故 A 正确;
第 5页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
对于 , ( )分母不能为 0,所以 ≠ 1,又 0 ≤ + 1 ≤ 2,得 1 ≤ ≤ 1,
所以 ( )的定义域为[ 1,1)故 B 不正确;
对于 ,若( 1)( 2) = 0,则 = 1 或 = 2,
所以“ = 2”是“( 1)( 2) = 0”的的充分不必要条件,故 C 错误;
对于 ,若函数 = 2 + + 的图象过点( 1,0),则 + = 0,
若 + = 0,则当 = 1 时, = + = 0,即函数 = 2 + + 的图象过点( 1,0),
“函数 = 2 + + 的图象过点( 1,0)”是“ + = 0”的充要条件,故 D 正确.故选: .
10.【答案】B D 解: 1 = 15 > 3; ≥ 2 时, ( 1) = 3 2 + 11 + 7 > 3 得 < 4,
所以 = 1,2,3.
11.【答案】 解:若 = , = + ,则 ( ) = + = + ,
所以 ( ) = + = ( ),所以 ( )是偶函数,A 正确;
若 = 1, = 2, = + 2 3,由 + 2 3 = 0 得 = 0 或 2,
所以函数 = 3 的零点为 0 和 ln2,B 正确;
若 = 1,设 = = 1 时,显然 ( ) < 0,C 错误;
若 = 为奇函数,则 ( ) = ( )恒成立,即 + = ( + ),
整理得( + )( + ) = 0 恒成立,即 = ,所以 ( ) = ,
从而 2 + 2 + ≤ 0 可转化为 2 + 2 + 0,
令 = ,则 2 + 2 = ( )2 + 2 = 2 + 2,即 2 + + 2 ≤ 0,
其中当 ∈ ( ∞,0)时, =
2
∈ ( ∞,0),所以 ≥ 2 =
2 ,
显然 = 2 = +
2
≥ 2 2,所以 的最小值为 2 2,D 正确.故选 ABD.
1 +1 1 1
12.【答案】 解:构造函数 = 2 +1 +1 ,则 = 2
(2 +1)+2
2 +1 2 +1+1 =
1
2 +
2 ,
2 +1+1
1
因为函数 = 2 +1在 上为单调递增函数,则 = 2 在 上为单调递减函数,2 +1+1
所以 ( )在 上为单调递减函数,所以 (2022) > (2023) > 0,即 > ,2 > 2 ,故选项 A 正确,选项 B
; 1 2
2022+1 1 22023+1 1
错误 因为 < = 2023 < 1, < = 2024 < 1,所以2 <
2 + 2 < 2,故选项 C 正确;
2 2 +1 2 2 +1
因为
+ ≥ 2 · = 2,当且仅当 = 时取等号,由题意可知 ≠ ,故 + ≠ 2,故选项 D 错误.故选 AC.
13.【答案】四
第 6页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
14. 1 3【答案】12 解:因为 > 0, > 0,且 + = 1,
所以 3 + = (3 + )( 1 3 + ) = 3 + 3 +
9
+ ≥ 6+ 2
9
· = 6 + 2 × 3 = 12,
当且仅当 = 3 ,即 = 2, = 6 时取等号,此时 3 + 的最小值为 12.
4
∞,2 5 ( ) = 2
2+9 9
15.【答案】 解: 22 = + 2 2,当 ∈ [1,2]时,
2 ∈ [1,4],当 2 = 3 时, ( ) = 4,
对 2 ∈ [2,3],总存在 1 ∈ [1,2]使得 ( 2) > ( 1)成立,
即 ∈ [2,3] ( ) > ( ) = 4,即 ( ) = 2 + 9 > 4,
2 5
得 ∈ 2,3 , < +5 = +
5,当 = 5时, + = 2 5.综上可知,实数 的取值范围为 ∞,2 5 . min
16.【答案】 0 ≤ ≤ 4 解: ①当 < 0 时,函数 ( )在( ∞, )上单调递减,因此 ( )不存在最大值;
9, < 0
②当 = 0 时, ( ) = 8 ( 3)2, ≥ 0,当 ≥ 0 时, ( )max = (3) = 8 > 9,故函数 ( )存在最大
值;
③当 0 < < 3 时,故函数 ( )在( , 3)上单调递增,在(3, + ∞)上单调递减,故 ≥ 时, ( ) = 8 (
3)2 ≤ 8,
当 < 时,函数 ( )在( ∞, )上单调递增,此时 ( ) < ( ) = 2 9.于是 2 9 ≤ 8 时函数存在最大
值.解得 0 < < 3.
④当 3 时,函数在( , + ∞)上单调递减, ( ) ≤ ( ) = 8 ( 3)2.
在( ∞, )上单调递增,此时 ( ) < ( ) = 2 9.故当 8 ( 3)2 ≥ 2 9,解得 1 ≤ ≤ 4,故 3 4;
综上,0 ≤ ≤ 4 时函数 ( )存在最大值.
17.解:(1)23+log25 + (log43 + log83)·(log32 + log92) = 8 × 5 +
5
6 log 3 ·
3 5 165
2 2 log32 = 40 + 4 = 4 . ……5 分
(2)因为 + = 12, = 9,所以 2 = + 2 4 = 36 × 3,得 = 6 3;……7 分
1 1 1 1 1 1
2 2 2 2 2 2 2
所以 1 1 =
( )
=
+ 2 · = 12 2 9 6 3 =
3
3 . ……10 分 2+ 2
18. (1) ( ) ( ) + = 1 1
解: 的定义域为 ,且 2 +1 2 + +
1 1
2 +1 2 =
2 1
1+2 + 2 +1 1 =
1 1 = 0,所以 ( )为奇函数;……6 分
(2) ( )在 上是奇函数且是减函数,……8 分
由不等式 ( 2 2 ) + (2 2 1) < 0 得 ( 2 2 ) < (2 2 1) = 1 2 2 ;……9 分
所以 2 2 > 1 2 2,即得{ | < 13或 > 1}. ……12 分
第 7页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
19.解:(1) 6 0.2 2按分层抽样, = 0.2+0.3 = 5,所以 = 15; ……3 分
(2)由频率分布直方图知,各区间频率为 0.17,0.20,0.30,0.25,0.08,
这组数据的平均数: = 0.17 × 200 + 0.20 × 300 + 0.30 × 400 + 0.25 × 500 + 0.08 × 600 = 387;……6 分
(3)方案 ①:根据题意可知 20000 个香瓜中:
200 克的有 0.17 × 20000 = 3400 个,300 克的有:0.20 × 20000 = 4000 个,
400 克的有:0.30 × 20000 = 6000 个,500 克的有:0.25 × 20000 = 5000 个,
600 克的有:0.08 × 20000 = 1600 个,
3400×200+4000×300+6000×400+5000×500+1600×600
500 × 5 = 77400 元; ……9 分
方案 ②:质量低于 350 克的香瓜有(0.17 + 0.20) × 20000 = 7400 个,
质量高于或等于 350 克的香瓜有 20000 7400 = 12600 个,
7400 × 3 + 12600 × 5 = 85200 元,且 85200 > 77400,……11 分
综上,种植园选择方案 ②获利更多. ……12 分
20.解:(1)由题意得 0 = 2, 1 = 1.94,所以当 = 1 时, 1 = 0 ( 0 1) 50.5+ ,
即 1.94 = 2 (2 1.94) 50.5+ ,解得 = 0.5,……3 分
所以 0.5 0.5 = 2 0.06 × 5 ∈ ,
故改良后所排放的废气中含有的污染物数量的函数模型为 = 2 0.06 × 50.5 0.5 ∈ . ……5 分
(2)由题意可得 = 2 0.06 × 50.5 0.5 ≤ 0.08,整理得50.5 0.5 ≥ 32,……6 分
两边同时取常用对数,得 0.5 0.5 ≥ lg32 5lg2lg5,整理得 ≥ 2 × 1 lg2 + 1,……9 分
2 = 0.3 2 × 5lg2 + 1 = 30将 代入,可得 1 lg2 7 + 1 ≈ 5.3,所以 ≥ 5.3,……11 分
又因为 ∈ ,所以 ≥ 6,
综上,至少进行 6 次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.……12 分
21.【答案】解:(1) ∵ = ( )具有“ (0)性质”∴ ( ) = ( )对 ∈ 恒成立∴ ( )是偶函数,……1 分
∴当 ∈ [0,1]时, ( ) = ( + )2 = ( )2,……3 分
∴当 ≤ 12时, ( ) = (1) = (1 )
2; ……5 分
1
当 > 2时, ( ) = (0) =
2. ……6 分
(2)函数 = ( )具有“性质 (2),则 ( + 2) = ( ),
当 ≥ 1 时, ( ) = | 4|,所以当 < 1 时,
第 8页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
| 4|, ≥ 1
( ) = ( + 2) = | + 2|,于是 ( ) = | + 2|, < 1 . ……8 分
函数 = 2 · + 有 8 个零点,令 = ( ),
则 2 + = 0 有两个不等的实数根 1, 2,且 0 < 1 < 3,0 < 2 < 3,……9 分
= 2 4 > 0
> 0
{ 9 9所以 32 3 + > 0,所以 4 < < 2 .所以 的取值范围为(4, 2 ). ……12 分
0 < 2 < 3
22.【答案】解:依题意 ( ) = log1 ,……1 分
2
(1) = 2 2 + 1 = log1( 2 2 + 1)在(1, + ∞)上单调递减,
2
令 ( ) = 2 2 + 1,则 ( )在(1, + ∞)上单调递增,且 ( ) > 0 对 ∈ (1, + ∞)恒成立.……3 分
∴ ≤ 1,且 (1) = 1 2 + 1 ≥ 0,∴ ≤ 1.故 的取值范围为( ∞,1].……5 分
(2)依题意有 2 > 0,且 4 + 2 6 > 0,∴ > 1. ……6 分
不等式log1( 2 ) < 2log1( + 2 6)在[4,9]上恒成立,
2 2
即 2 > ( + 2 6)2在[4,9]上恒成立,……7分
∴ > + 2 6,∴ ( 2) > 6 在[4,9]上恒成立,
当 = 4 6 6时不等式成立,所以必须 > 2在(4,9]上恒成立∴ > ( 2 )max……9分
6 2 2 = ∈ (0,1] = +4 2 = 2 2令 , , ,而 2 + 4 + 4 在(0,1]上单调递增,
∴ ( 2 + 4)max = 3,∴ > 3
综上: 的取值范围为(3, + ∞).……12分
第 9页
{#{QQABCYAAogioAAJAARgCAQ36CEGQkBAAACoOQEAMIAABgANABAA=}#}
同课章节目录
