人教A版(2019)选择性必修 第一册 3.1 椭圆 教案
文档属性
| 名称 | 人教A版(2019)选择性必修 第一册 3.1 椭圆 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 225.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 22:06:03 | ||
图片预览


文档简介
【课题】 椭圆
【教学目标】
1.理解椭圆的定义,理解焦点在x轴与焦点在y轴的两种椭圆的标准方程.
2.通过椭圆的标准方程的推导,理解“解析法”的应用,从而学生的数学思维能力得到提高.
【教学重点】
椭圆两种形式的标准方程.
【教学难点】
标准方程的推导.
【教学设计】
通过师生的共同操作实验,引入知识.椭圆的定义中要强调“常数”大于,否则画不出图形.标准方程的推导是本节教学难点之一.直接给出焦点在y轴上的椭圆的图形,图中显示出椭圆与坐标系之间的种位置关系.然后看图说话,类比介绍焦点在y轴上的椭圆的标准方程.例1是求椭圆的标准方程的训练题.求椭圆的标准方程,关键是确定焦点的位置和求出和.例1给出了焦点的位置并给出了2和2,方便地求出和,利用关系式求出.例2是已知椭圆的标准方程,求焦距和焦点坐标的训练题.经过例1和例2的训练,从两个不同的角度强化学生对两类椭圆的标准方程特征的认识,及关系式的掌握.
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
教 学 过 程 教师行为 学生行为 教学意图 时间
*揭示课题椭圆*创设情境 兴趣导入我们已经学习过直线与圆的方程.知道二元一次方程为直线的方程,二元二次方程为圆的方程.下面将陆续研究一些新的二元二次方程及其对应的曲线. 介绍播放课件质疑 了解观看课件思考 引导启发学生得出结果 05
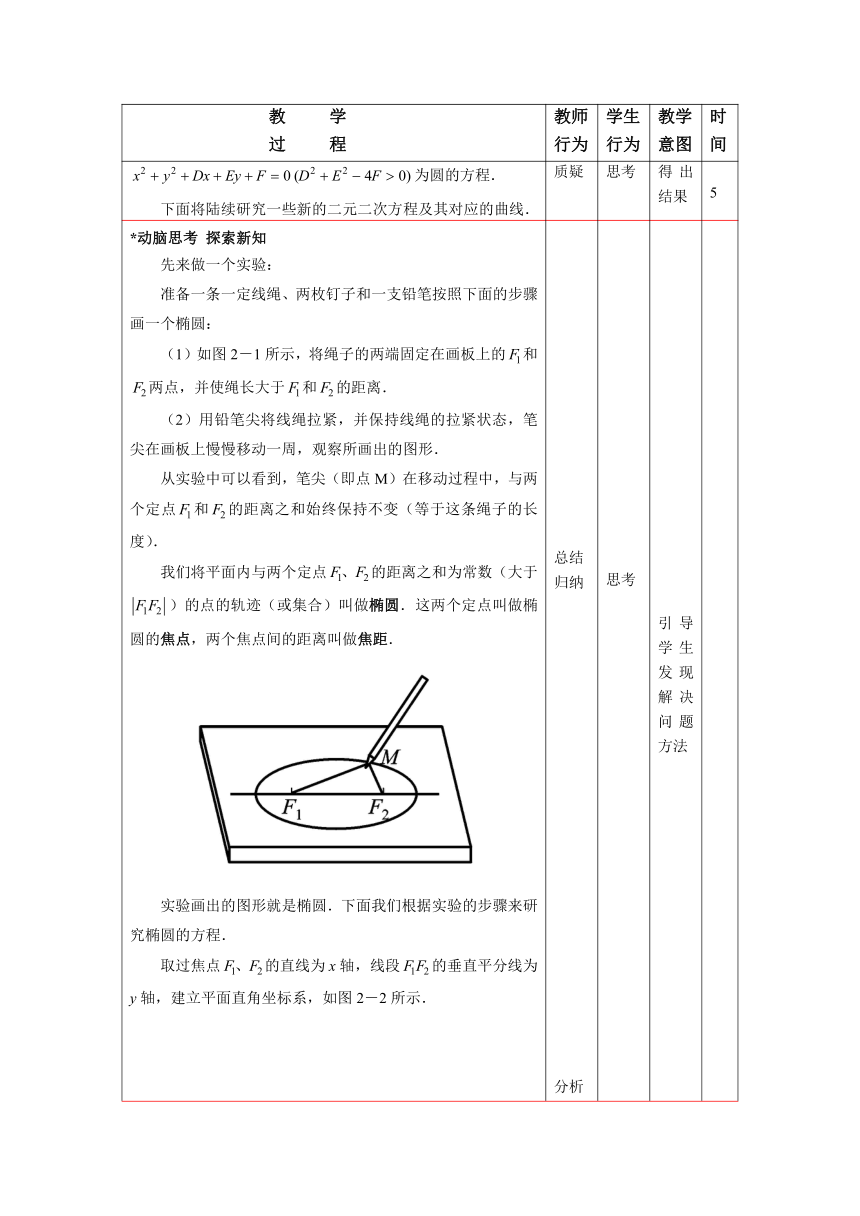
*动脑思考 探索新知先来做一个实验:准备一条一定线绳、两枚钉子和一支铅笔按照下面的步骤画一个椭圆:(1)如图2-1所示,将绳子的两端固定在画板上的和两点,并使绳长大于和的距离. (2)用铅笔尖将线绳拉紧,并保持线绳的拉紧状态,笔尖在画板上慢慢移动一周,观察所画出的图形. 从实验中可以看到,笔尖(即点M)在移动过程中,与两个定点和的距离之和始终保持不变(等于这条绳子的长度).我们将平面内与两个定点的距离之和为常数(大于)的点的轨迹(或集合)叫做椭圆.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做焦距.实验画出的图形就是椭圆.下面我们根据实验的步骤来研究椭圆的方程.取过焦点的直线为x轴,线段的垂直平分线为y轴,建立平面直角坐标系,如图2-2所示.设M(x,y)是椭圆上的任意一点,椭圆的焦距为2c(c>0),椭圆上的点与两个定点的距离之和为2a(a>0),则的坐标分别为(-c,0),(c,0),由条件得移项得 两边平方得整理得 两边平方后,整理得 由椭圆的定义得2a>2c>0,即a>c>0,所以,设,则【小提示】设,不仅使得方程变得简单规整,同时在后面讨论椭圆的集合性质时,还会看到它有明确的几何意义.等式两边同时除以得 (2.1)方程(2.1)叫做焦点在x轴上的椭圆的标准方程.它所表示的椭圆的焦点是并且如图2-3所示,如果取过焦点的直线为y轴,线段的垂直平分线为x轴,建立平面直角坐标系,用类似的方法可以得到椭圆的标准方程为 (2.2)图2-3 方程(2.2)叫做焦点在y轴上的椭圆的标准方程.字母a、b的意义同上,并且【想一想】已知一个椭圆的标准方程,如何判定焦点在x轴还是在y轴? 总结归纳分析关键词语 思考理解记忆 引导学生发现解决问题方法 25
*巩固知识 典型例题例1 已知椭圆的焦点在x轴上,焦距为8,椭圆上的点到两个焦点的距离之和为10.求椭圆的标准方程. 解 由于2c=8,2a=10,即c=4,a=5,所以由于椭圆的焦点在x轴上,因此椭圆的标准方程为 即 【想一想】将例1中的条件“椭圆的焦点在x轴上”去掉,其余的条件不变,你能写出椭圆的标准方程吗?例2 求下列椭圆的焦点和焦距.(1); (2).分析 解题关键是判断椭圆的焦点在哪条坐标轴上.方法是观察标准方程中含x项与含y项的分母,哪项的分母大,焦点就在哪个数轴.解 (1)因为5>4,所以椭圆的焦点在x轴上,并且故 因此 c=4,2c=2.所以,椭圆的焦点为焦距为2.(2)将方程化成标准方程,为.因为16>8,所以椭圆的焦点在y轴上,并且故 .因此 , 所以,椭圆的焦点为焦距为 引领讲解说明 观察思考主动求解 注意观察学生是否理解知识点 45
*运用知识 强化练习 1.已知椭圆的焦点为椭圆上的点到两个焦点的距离之和为8.求椭圆的标准方程.2.写出下列椭圆的焦点坐标和焦距.(1); (2). 提问巡视指导 动手求解 及时了解学生知识掌握情况 60
*理论升华 整体建构思考并回答下面的问题:分别写出焦点在x轴和焦点在y轴上的椭圆的标准方程.结论:焦点在x轴上的椭圆的标准方程是焦点在y轴上的椭圆的标准方程是 质疑归纳强调 回答理解强化 师生共同归纳强调重点 70
*归纳小结 强化思想本次课学了哪些内容?重点和难点各是什么? 引导 回忆 75
*自我反思 目标检测 本次课采用了怎样的学习方法?你是如何进行学习的?你的学习效果如何?已知椭圆的焦距为6,椭圆上的点到两个焦点的距离之和为10.求椭圆的标准方程. 提问巡视指导 反思动手求解 培养反思学习过程的能力 85
*继续探索 活动探究(1)读书部分:教材(2)书面作业:教材习题2.1(必做);学习指导2.1(选做)(3)实践调查:运用本课所学知识,解决实际问题 说明 记录 分层次要求 90
【教师教学后记】
项目 反思点
学生知识、技能的掌握情况 学生是否真正理解有关知识;是否能利用知识、技能解决问题;在知识、技能的掌握上存在哪些问题;
学生的情感态度 学生是否参与有关活动;在数学活动中,是否认真、积极、自信;遇到困难时,是否愿意通过自己的努力加以克服;
学生思维情况 学生是否积极思考;思维是否有条理、灵活;是否能提出新的想法;是否自觉地进行反思;
学生合作交流的情况 学生是否善于与人合作;在交流中,是否积极表达;是否善于倾听别人的意见;
学生实践的情况 学生是否愿意开展实践;能否根据问题合理地进行实践;在实践中能否积极思考;能否有意识的反思实践过程的方面;
图2-2
【教学目标】
1.理解椭圆的定义,理解焦点在x轴与焦点在y轴的两种椭圆的标准方程.
2.通过椭圆的标准方程的推导,理解“解析法”的应用,从而学生的数学思维能力得到提高.
【教学重点】
椭圆两种形式的标准方程.
【教学难点】
标准方程的推导.
【教学设计】
通过师生的共同操作实验,引入知识.椭圆的定义中要强调“常数”大于,否则画不出图形.标准方程的推导是本节教学难点之一.直接给出焦点在y轴上的椭圆的图形,图中显示出椭圆与坐标系之间的种位置关系.然后看图说话,类比介绍焦点在y轴上的椭圆的标准方程.例1是求椭圆的标准方程的训练题.求椭圆的标准方程,关键是确定焦点的位置和求出和.例1给出了焦点的位置并给出了2和2,方便地求出和,利用关系式求出.例2是已知椭圆的标准方程,求焦距和焦点坐标的训练题.经过例1和例2的训练,从两个不同的角度强化学生对两类椭圆的标准方程特征的认识,及关系式的掌握.
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
教 学 过 程 教师行为 学生行为 教学意图 时间
*揭示课题椭圆*创设情境 兴趣导入我们已经学习过直线与圆的方程.知道二元一次方程为直线的方程,二元二次方程为圆的方程.下面将陆续研究一些新的二元二次方程及其对应的曲线. 介绍播放课件质疑 了解观看课件思考 引导启发学生得出结果 05
*动脑思考 探索新知先来做一个实验:准备一条一定线绳、两枚钉子和一支铅笔按照下面的步骤画一个椭圆:(1)如图2-1所示,将绳子的两端固定在画板上的和两点,并使绳长大于和的距离. (2)用铅笔尖将线绳拉紧,并保持线绳的拉紧状态,笔尖在画板上慢慢移动一周,观察所画出的图形. 从实验中可以看到,笔尖(即点M)在移动过程中,与两个定点和的距离之和始终保持不变(等于这条绳子的长度).我们将平面内与两个定点的距离之和为常数(大于)的点的轨迹(或集合)叫做椭圆.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做焦距.实验画出的图形就是椭圆.下面我们根据实验的步骤来研究椭圆的方程.取过焦点的直线为x轴,线段的垂直平分线为y轴,建立平面直角坐标系,如图2-2所示.设M(x,y)是椭圆上的任意一点,椭圆的焦距为2c(c>0),椭圆上的点与两个定点的距离之和为2a(a>0),则的坐标分别为(-c,0),(c,0),由条件得移项得 两边平方得整理得 两边平方后,整理得 由椭圆的定义得2a>2c>0,即a>c>0,所以,设,则【小提示】设,不仅使得方程变得简单规整,同时在后面讨论椭圆的集合性质时,还会看到它有明确的几何意义.等式两边同时除以得 (2.1)方程(2.1)叫做焦点在x轴上的椭圆的标准方程.它所表示的椭圆的焦点是并且如图2-3所示,如果取过焦点的直线为y轴,线段的垂直平分线为x轴,建立平面直角坐标系,用类似的方法可以得到椭圆的标准方程为 (2.2)图2-3 方程(2.2)叫做焦点在y轴上的椭圆的标准方程.字母a、b的意义同上,并且【想一想】已知一个椭圆的标准方程,如何判定焦点在x轴还是在y轴? 总结归纳分析关键词语 思考理解记忆 引导学生发现解决问题方法 25
*巩固知识 典型例题例1 已知椭圆的焦点在x轴上,焦距为8,椭圆上的点到两个焦点的距离之和为10.求椭圆的标准方程. 解 由于2c=8,2a=10,即c=4,a=5,所以由于椭圆的焦点在x轴上,因此椭圆的标准方程为 即 【想一想】将例1中的条件“椭圆的焦点在x轴上”去掉,其余的条件不变,你能写出椭圆的标准方程吗?例2 求下列椭圆的焦点和焦距.(1); (2).分析 解题关键是判断椭圆的焦点在哪条坐标轴上.方法是观察标准方程中含x项与含y项的分母,哪项的分母大,焦点就在哪个数轴.解 (1)因为5>4,所以椭圆的焦点在x轴上,并且故 因此 c=4,2c=2.所以,椭圆的焦点为焦距为2.(2)将方程化成标准方程,为.因为16>8,所以椭圆的焦点在y轴上,并且故 .因此 , 所以,椭圆的焦点为焦距为 引领讲解说明 观察思考主动求解 注意观察学生是否理解知识点 45
*运用知识 强化练习 1.已知椭圆的焦点为椭圆上的点到两个焦点的距离之和为8.求椭圆的标准方程.2.写出下列椭圆的焦点坐标和焦距.(1); (2). 提问巡视指导 动手求解 及时了解学生知识掌握情况 60
*理论升华 整体建构思考并回答下面的问题:分别写出焦点在x轴和焦点在y轴上的椭圆的标准方程.结论:焦点在x轴上的椭圆的标准方程是焦点在y轴上的椭圆的标准方程是 质疑归纳强调 回答理解强化 师生共同归纳强调重点 70
*归纳小结 强化思想本次课学了哪些内容?重点和难点各是什么? 引导 回忆 75
*自我反思 目标检测 本次课采用了怎样的学习方法?你是如何进行学习的?你的学习效果如何?已知椭圆的焦距为6,椭圆上的点到两个焦点的距离之和为10.求椭圆的标准方程. 提问巡视指导 反思动手求解 培养反思学习过程的能力 85
*继续探索 活动探究(1)读书部分:教材(2)书面作业:教材习题2.1(必做);学习指导2.1(选做)(3)实践调查:运用本课所学知识,解决实际问题 说明 记录 分层次要求 90
【教师教学后记】
项目 反思点
学生知识、技能的掌握情况 学生是否真正理解有关知识;是否能利用知识、技能解决问题;在知识、技能的掌握上存在哪些问题;
学生的情感态度 学生是否参与有关活动;在数学活动中,是否认真、积极、自信;遇到困难时,是否愿意通过自己的努力加以克服;
学生思维情况 学生是否积极思考;思维是否有条理、灵活;是否能提出新的想法;是否自觉地进行反思;
学生合作交流的情况 学生是否善于与人合作;在交流中,是否积极表达;是否善于倾听别人的意见;
学生实践的情况 学生是否愿意开展实践;能否根据问题合理地进行实践;在实践中能否积极思考;能否有意识的反思实践过程的方面;
图2-2
