2024河南中考数学备考重难专题:综合与实践 旋转问题 导学案(含答案)
文档属性
| 名称 | 2024河南中考数学备考重难专题:综合与实践 旋转问题 导学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 204.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览



文档简介
2024河南中考数学备考重难专题:综合与实践 旋转问题 导学案
考情分析
年份 题号 题型 分值 设问 解题关键点
2023 23 解 答 题 11 (1)三角形的形状为____,线段的比值 (2)①(1)中的两个结论是否成立?成立请证明,不成立请说明理由 ②当四边形为平行四边形时,请直接写出线段比 (1)证明三角形两个内角为45°;连接正方形对角线BD,构造△B'DB∽△EDC(手拉手相似) (2)①证明三角形两个内角为45°;连接正方形对角线BD,构造△B'DB∽△EDC(手拉手相似) ②分类讨论:当点B'在BE上,当点B'在BE的延长线上(类比(1)(2)问B'分别在BE及BE延长线上)
2022 22 10 (1)两线段的比值是____,角的度数是___ (2)写出线段比值及两线段相交所成的较小角度数 (3)直接写出线段比值 (1)证明三角形全等;延长两条线段所交锐角,根据全等三角形对应角相等将角转化到一个三角形中,根据内角和求解 (2)证明三角形相似;根据相似三角形对应角相等将角转化到一个三角形中,根据内角和求解 (3)分类讨论:当点P在在线段EF上,和点P在FE的延长线上(类比(1)(2)问P分别在三角形内部和外部)
2021 22 10 (1)①线段比的值为____ ②角的度数为____ (2)请判断线段比值及角的度数 (3)请直接写出当点C与点M重合时AC的长 (1)①证明三角形全等 ②根据全等三角形对应角相等将角转化到一个三角形中,根据内角和求解 (2)证明三角形相似; 根据相似三角形对应角相等将角转化到一个三角形中,根据内角和求解 (3)当点C与点M垂合时,B、D、C三点共线,通过构造直角三角形求线段长
2020 22 10 (1)两线段的数量关系是____,位置关系是____ (2)判断三角形的形状,并说明理由 (3)直接写出三角形面积最大值 (1)MP=EC=BD=PN;两条线段平行,垂直于其中一条线段的垂线,也垂直于另一条平行线 (2)MP=EC=BD=PN; (3)当CE最大时,MP最大;当点C、E在点A异侧,且在同一条直线上时,CE最大
典例精讲
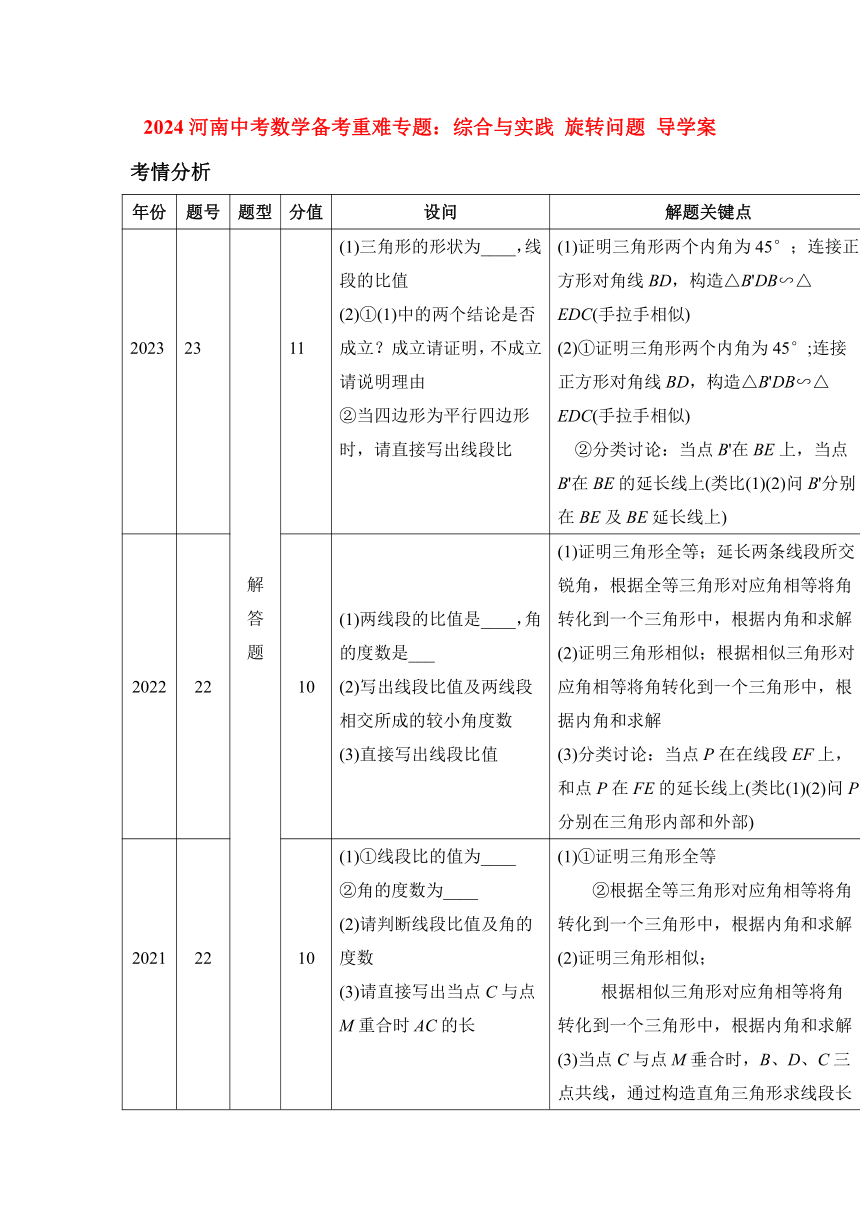
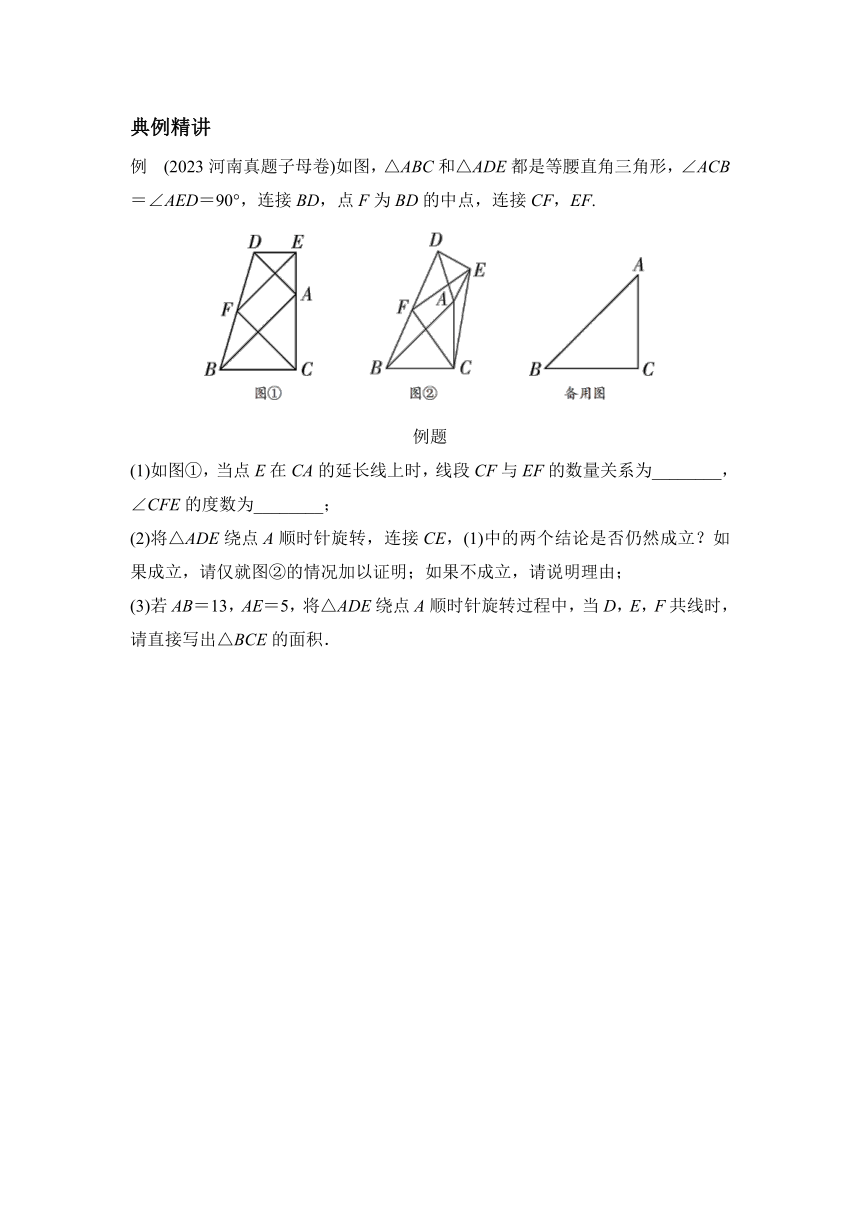
例 (2023河南真题子母卷)如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠AED=90°,连接BD,点F为BD的中点,连接CF,EF.
例题
(1)如图①,当点E在CA的延长线上时,线段CF与EF的数量关系为________,∠CFE的度数为________;
(2)将△ADE绕点A顺时针旋转,连接CE,(1)中的两个结论是否仍然成立?如果成立,请仅就图②的情况加以证明;如果不成立,请说明理由;
(3)若AB=13,AE=5,将△ADE绕点A顺时针旋转过程中,当D,E,F共线时,请直接写出△BCE的面积.
课堂练兵
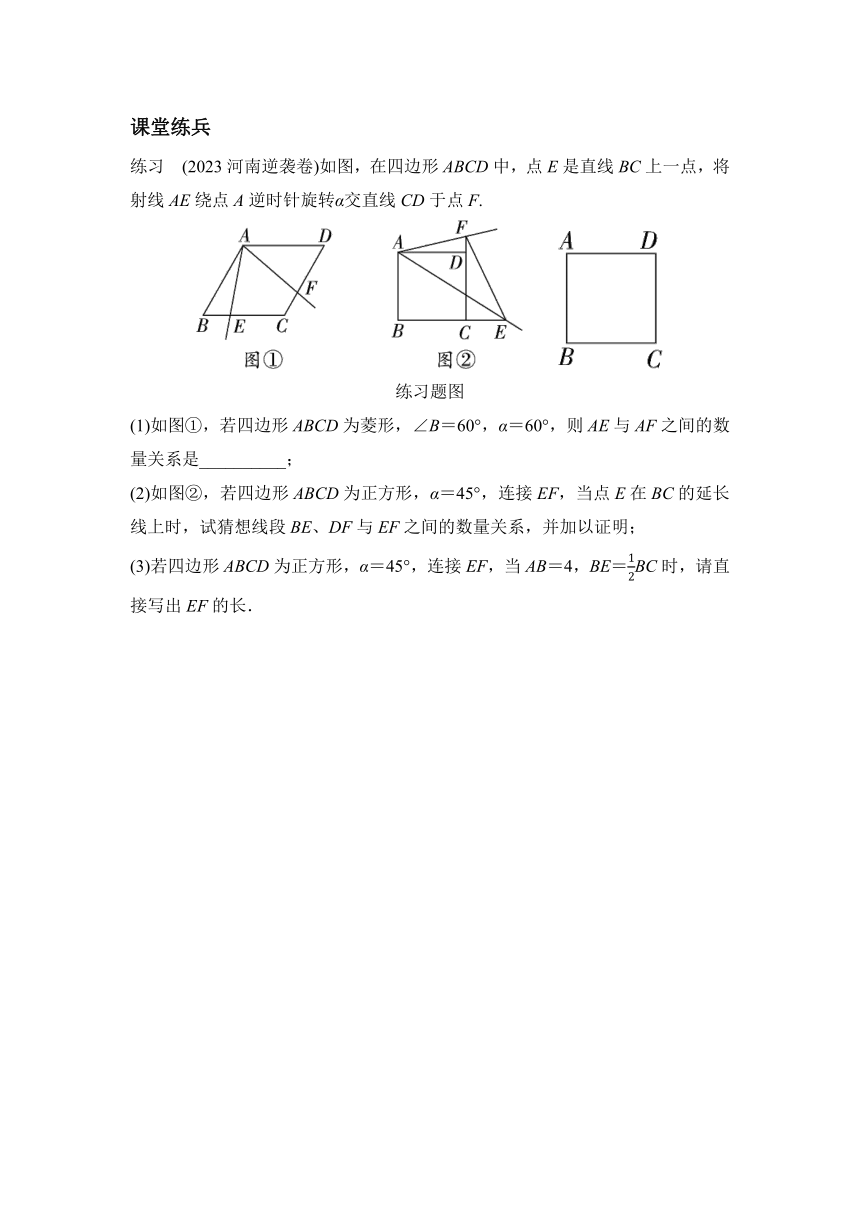
练习 (2023河南逆袭卷)如图,在四边形ABCD中,点E是直线BC上一点,将射线AE绕点A逆时针旋转α交直线CD于点F.
练习题图
(1)如图①,若四边形ABCD为菱形,∠B=60°,α=60°,则AE与AF之间的数量关系是__________;
(2)如图②,若四边形ABCD为正方形,α=45°,连接EF,当点E在BC的延长线上时,试猜想线段BE、DF与EF之间的数量关系,并加以证明;
(3)若四边形ABCD为正方形,α=45°,连接EF,当AB=4,BE=BC时,请直接写出EF的长.
课后小练
练习 (2023河南预测卷)如图,△AOB和△COD是等腰直角三角形,OA=2OC=4,点O为直角顶点,连接AD、BC,E是BC的中点,连接OE.
练习题图
(1)如图①,当点C、D分别在边OA、OB上时,线段OE与线段AD之间的数量关系为________;
(2)将△COD绕点O逆时针旋转到如图②所示位置,请探究线段OE与线段AD之间的数量关系,并说明理由;
(3)在△COD的旋转过程中,当点C落在直线AD上时,请直接写出OE的长.
答案
典例精讲
例 解:(1)EF=CF,90°;
【解法提示】如解图①,连接AF,∵△ABC和△ADE都是等腰直角三角形,∴∠DEA=∠BCA=90°,AE=DE,AC=BC,∴∠DAB=90°,∵点F为BD的中点,∴AF=DF=BF,∴△AEF≌△DEF(SSS),∴∠AEF=∠DEF,∵∠AED=90°,∴∠AEF=45°,同理可得∠ACF=45°,∴∠AEF=∠ACF=45°,∴EF=CF,∠CFE=90°.
解图①
(2)(1)中的两个结论仍成立.
证明:∵△ABC和△ADE都是等腰直角三角形,
∴∠ABC=∠BAC=∠ADE=∠DAE=45°,AE=DE,AC=BC,
如解图②,过点B作BG∥DE交EF的延长线于点G,连接CG,
解图②
∵BG∥DE,
∴∠EDF=∠GBF,
∵∠DFE=∠BFG,BF=DF,
∴△BFG≌△DFE(ASA),
∴BG=DE,FG=EF,∴BG=AE,
∵∠EDF=∠GBF,
∴∠CBG=∠GBF+∠CBD=∠EDF+∠CBD
=∠ABD+∠ADB+∠ABC+∠ADE
=180°-∠BAD+45°+45°
=270°-∠BAD=∠EAC,
在△BGC和△AEC中,
∴△BGC≌△AEC(SAS),
∴GC=EC,∠BCG=∠ACE,
∵∠ACB=∠BCG+∠ACG=90°,
∴∠ACE+∠ACG=90°,
∴△ECG是等腰直角三角形,
又∵FG=EF,
∴EF=CF,∠CFE=90°;
(3)51或21.
【解法提示】①如解图③,在△ABE中,∠AEB=90°,AB=13,AE=5,由勾股定理得BE===12,∴BD=BE-DE=12-5=7,∵点F是BD的中点,∴DF=,∴CF=EF=5+=,∴S△BCE=BE·CF=×12×=51;②如解图④,同理可得S△BCE=BE·CF=×12×=21.综上所述,△BCE的面积为51或21.
解图③ 解图④
课堂练兵
练习 解:(1)AE=AF;
【解法提示】如解图①,连接AC,∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∴∠ACD=∠BAC.∵∠B=60°,∴△ABC是等边三角形,∴AB=AC,∠ACD=∠BAC=60°.∵∠EAF=60°,∴∠BAE+∠EAC=∠EAC+∠CAF=60°,∴∠BAE=∠CAF,∴△ABE≌△ACF,∴AE=AF.
解图① 解图②
(2)BE-DF=EF;
证明:如解图②,在BC上取点F′,使得BF′=DF,连接AF′,
∵四边形ABCD是正方形,
∴AB=AD,∠ABF′=∠ADF=90°,
在△ABF′和△ADF中,,
∴△ABF′≌△ADF(SAS),
∴AF′=AF,∠BAF′=∠DAF.
∵∠EAF=45°,∠BAD=90°,
∴∠DAE+∠DAF=∠DAE+∠BAF′=45°,
∴∠EAF′=∠EAF=45°.
在△AEF′和△AEF中,,
∴△AEF′≌△AEF(SAS),∴EF′=EF,
∴BE-DF=BE-BF′=EF′=EF;
(3)或10.
【解法提示】分两种情况:①如解图③,当点E在线段BC上时,同理(2)易得EF=BE+DF,∵AB=4,∴BE=BC=2.设EF=x,则DF=x-2,CF=4-(x-2)=6-x,在Rt△CEF中,由勾股定理得CE2+CF2=EF2,即22+(6-x)2=x2,解得x=,即EF=;②如解图④,当点E在CB延长线上时,同理可得DF-BE=EF.设EF=x,则DF=x+2,CF=x+2-4=x-2,在Rt△CEF中,由勾股定理得CE2+CF2=EF2,即62+(x-2)2=x2,解得x=10,即EF=10.综上所述,EF的长为或10.
解图
课后小练
练习 解:(1)OE=AD;
【解法提示】∵△AOB和△COD是等腰直角三角形,点C、D分别在边OA、OB上,∴OA=OB,OC=OD,∠AOD=∠BOC=90°,∴△AOD≌△BOC,∴AD=BC.∵E为BC的中点,∴OE=BC,∴OE=AD.
(2)OE=AD,
理由如下:如解图①,延长OE至点F,使得EF=OE,连接BF、CF,
∵BE=CE,EO=EF,
∴四边形COBF是平行四边形,∴BF∥CO,BF=CO=DO,∴∠FBO+∠BOC=180°.
∵∠BOA=∠COD=90°,
∴∠BOC+∠BOD=∠1+∠BOD=90°,∴∠1=∠BOC.
∵∠1+∠DOA=180°,
∴∠FBO=∠DOA.
∵BO=AO,
∴△FBO≌△DOA(SAS),∴AD=OF,∴OE=AD;
解图①
(3)+1或-1.
【解法提示】分点C在AD上和点C在AD的延长线上两种情况讨论:①如解图②,当点C在线段AD上时,设AD、EO交于点M,由(2)可知EO=AD,易证AD⊥EO,∴∠AMO=90°,∵OC=OD=2,∴MO==2,∴在Rt△AMO中,AM===2,又∵MD=MO=2,∴AD=AM+MD=2+2,∴OE=AD=+1;②如解图③,当点C在AD的延长线上时,延长EO交AC于点N,由(2)可知EO=AD,易证AD⊥EO,∴AC⊥EN,∴∠ANO=90°,∵OC=OD=2,∴NO==2,∴在Rt△ANO中,AN===2,又∵DN=NO=2,∴AD=AN-DN=2-2,∴OE=AD=-1.
解图
考情分析
年份 题号 题型 分值 设问 解题关键点
2023 23 解 答 题 11 (1)三角形的形状为____,线段的比值 (2)①(1)中的两个结论是否成立?成立请证明,不成立请说明理由 ②当四边形为平行四边形时,请直接写出线段比 (1)证明三角形两个内角为45°;连接正方形对角线BD,构造△B'DB∽△EDC(手拉手相似) (2)①证明三角形两个内角为45°;连接正方形对角线BD,构造△B'DB∽△EDC(手拉手相似) ②分类讨论:当点B'在BE上,当点B'在BE的延长线上(类比(1)(2)问B'分别在BE及BE延长线上)
2022 22 10 (1)两线段的比值是____,角的度数是___ (2)写出线段比值及两线段相交所成的较小角度数 (3)直接写出线段比值 (1)证明三角形全等;延长两条线段所交锐角,根据全等三角形对应角相等将角转化到一个三角形中,根据内角和求解 (2)证明三角形相似;根据相似三角形对应角相等将角转化到一个三角形中,根据内角和求解 (3)分类讨论:当点P在在线段EF上,和点P在FE的延长线上(类比(1)(2)问P分别在三角形内部和外部)
2021 22 10 (1)①线段比的值为____ ②角的度数为____ (2)请判断线段比值及角的度数 (3)请直接写出当点C与点M重合时AC的长 (1)①证明三角形全等 ②根据全等三角形对应角相等将角转化到一个三角形中,根据内角和求解 (2)证明三角形相似; 根据相似三角形对应角相等将角转化到一个三角形中,根据内角和求解 (3)当点C与点M垂合时,B、D、C三点共线,通过构造直角三角形求线段长
2020 22 10 (1)两线段的数量关系是____,位置关系是____ (2)判断三角形的形状,并说明理由 (3)直接写出三角形面积最大值 (1)MP=EC=BD=PN;两条线段平行,垂直于其中一条线段的垂线,也垂直于另一条平行线 (2)MP=EC=BD=PN; (3)当CE最大时,MP最大;当点C、E在点A异侧,且在同一条直线上时,CE最大
典例精讲
例 (2023河南真题子母卷)如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠AED=90°,连接BD,点F为BD的中点,连接CF,EF.
例题
(1)如图①,当点E在CA的延长线上时,线段CF与EF的数量关系为________,∠CFE的度数为________;
(2)将△ADE绕点A顺时针旋转,连接CE,(1)中的两个结论是否仍然成立?如果成立,请仅就图②的情况加以证明;如果不成立,请说明理由;
(3)若AB=13,AE=5,将△ADE绕点A顺时针旋转过程中,当D,E,F共线时,请直接写出△BCE的面积.
课堂练兵
练习 (2023河南逆袭卷)如图,在四边形ABCD中,点E是直线BC上一点,将射线AE绕点A逆时针旋转α交直线CD于点F.
练习题图
(1)如图①,若四边形ABCD为菱形,∠B=60°,α=60°,则AE与AF之间的数量关系是__________;
(2)如图②,若四边形ABCD为正方形,α=45°,连接EF,当点E在BC的延长线上时,试猜想线段BE、DF与EF之间的数量关系,并加以证明;
(3)若四边形ABCD为正方形,α=45°,连接EF,当AB=4,BE=BC时,请直接写出EF的长.
课后小练
练习 (2023河南预测卷)如图,△AOB和△COD是等腰直角三角形,OA=2OC=4,点O为直角顶点,连接AD、BC,E是BC的中点,连接OE.
练习题图
(1)如图①,当点C、D分别在边OA、OB上时,线段OE与线段AD之间的数量关系为________;
(2)将△COD绕点O逆时针旋转到如图②所示位置,请探究线段OE与线段AD之间的数量关系,并说明理由;
(3)在△COD的旋转过程中,当点C落在直线AD上时,请直接写出OE的长.
答案
典例精讲
例 解:(1)EF=CF,90°;
【解法提示】如解图①,连接AF,∵△ABC和△ADE都是等腰直角三角形,∴∠DEA=∠BCA=90°,AE=DE,AC=BC,∴∠DAB=90°,∵点F为BD的中点,∴AF=DF=BF,∴△AEF≌△DEF(SSS),∴∠AEF=∠DEF,∵∠AED=90°,∴∠AEF=45°,同理可得∠ACF=45°,∴∠AEF=∠ACF=45°,∴EF=CF,∠CFE=90°.
解图①
(2)(1)中的两个结论仍成立.
证明:∵△ABC和△ADE都是等腰直角三角形,
∴∠ABC=∠BAC=∠ADE=∠DAE=45°,AE=DE,AC=BC,
如解图②,过点B作BG∥DE交EF的延长线于点G,连接CG,
解图②
∵BG∥DE,
∴∠EDF=∠GBF,
∵∠DFE=∠BFG,BF=DF,
∴△BFG≌△DFE(ASA),
∴BG=DE,FG=EF,∴BG=AE,
∵∠EDF=∠GBF,
∴∠CBG=∠GBF+∠CBD=∠EDF+∠CBD
=∠ABD+∠ADB+∠ABC+∠ADE
=180°-∠BAD+45°+45°
=270°-∠BAD=∠EAC,
在△BGC和△AEC中,
∴△BGC≌△AEC(SAS),
∴GC=EC,∠BCG=∠ACE,
∵∠ACB=∠BCG+∠ACG=90°,
∴∠ACE+∠ACG=90°,
∴△ECG是等腰直角三角形,
又∵FG=EF,
∴EF=CF,∠CFE=90°;
(3)51或21.
【解法提示】①如解图③,在△ABE中,∠AEB=90°,AB=13,AE=5,由勾股定理得BE===12,∴BD=BE-DE=12-5=7,∵点F是BD的中点,∴DF=,∴CF=EF=5+=,∴S△BCE=BE·CF=×12×=51;②如解图④,同理可得S△BCE=BE·CF=×12×=21.综上所述,△BCE的面积为51或21.
解图③ 解图④
课堂练兵
练习 解:(1)AE=AF;
【解法提示】如解图①,连接AC,∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∴∠ACD=∠BAC.∵∠B=60°,∴△ABC是等边三角形,∴AB=AC,∠ACD=∠BAC=60°.∵∠EAF=60°,∴∠BAE+∠EAC=∠EAC+∠CAF=60°,∴∠BAE=∠CAF,∴△ABE≌△ACF,∴AE=AF.
解图① 解图②
(2)BE-DF=EF;
证明:如解图②,在BC上取点F′,使得BF′=DF,连接AF′,
∵四边形ABCD是正方形,
∴AB=AD,∠ABF′=∠ADF=90°,
在△ABF′和△ADF中,,
∴△ABF′≌△ADF(SAS),
∴AF′=AF,∠BAF′=∠DAF.
∵∠EAF=45°,∠BAD=90°,
∴∠DAE+∠DAF=∠DAE+∠BAF′=45°,
∴∠EAF′=∠EAF=45°.
在△AEF′和△AEF中,,
∴△AEF′≌△AEF(SAS),∴EF′=EF,
∴BE-DF=BE-BF′=EF′=EF;
(3)或10.
【解法提示】分两种情况:①如解图③,当点E在线段BC上时,同理(2)易得EF=BE+DF,∵AB=4,∴BE=BC=2.设EF=x,则DF=x-2,CF=4-(x-2)=6-x,在Rt△CEF中,由勾股定理得CE2+CF2=EF2,即22+(6-x)2=x2,解得x=,即EF=;②如解图④,当点E在CB延长线上时,同理可得DF-BE=EF.设EF=x,则DF=x+2,CF=x+2-4=x-2,在Rt△CEF中,由勾股定理得CE2+CF2=EF2,即62+(x-2)2=x2,解得x=10,即EF=10.综上所述,EF的长为或10.
解图
课后小练
练习 解:(1)OE=AD;
【解法提示】∵△AOB和△COD是等腰直角三角形,点C、D分别在边OA、OB上,∴OA=OB,OC=OD,∠AOD=∠BOC=90°,∴△AOD≌△BOC,∴AD=BC.∵E为BC的中点,∴OE=BC,∴OE=AD.
(2)OE=AD,
理由如下:如解图①,延长OE至点F,使得EF=OE,连接BF、CF,
∵BE=CE,EO=EF,
∴四边形COBF是平行四边形,∴BF∥CO,BF=CO=DO,∴∠FBO+∠BOC=180°.
∵∠BOA=∠COD=90°,
∴∠BOC+∠BOD=∠1+∠BOD=90°,∴∠1=∠BOC.
∵∠1+∠DOA=180°,
∴∠FBO=∠DOA.
∵BO=AO,
∴△FBO≌△DOA(SAS),∴AD=OF,∴OE=AD;
解图①
(3)+1或-1.
【解法提示】分点C在AD上和点C在AD的延长线上两种情况讨论:①如解图②,当点C在线段AD上时,设AD、EO交于点M,由(2)可知EO=AD,易证AD⊥EO,∴∠AMO=90°,∵OC=OD=2,∴MO==2,∴在Rt△AMO中,AM===2,又∵MD=MO=2,∴AD=AM+MD=2+2,∴OE=AD=+1;②如解图③,当点C在AD的延长线上时,延长EO交AC于点N,由(2)可知EO=AD,易证AD⊥EO,∴AC⊥EN,∴∠ANO=90°,∵OC=OD=2,∴NO==2,∴在Rt△ANO中,AN===2,又∵DN=NO=2,∴AD=AN-DN=2-2,∴OE=AD=-1.
解图
同课章节目录
