人教版 八年级上册 第十二章 全等三角形《角平分线的性质》说课稿课件.(共18张PPT)
文档属性
| 名称 | 人教版 八年级上册 第十二章 全等三角形《角平分线的性质》说课稿课件.(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
角平分线的性质
(第1课时)
说教法学法
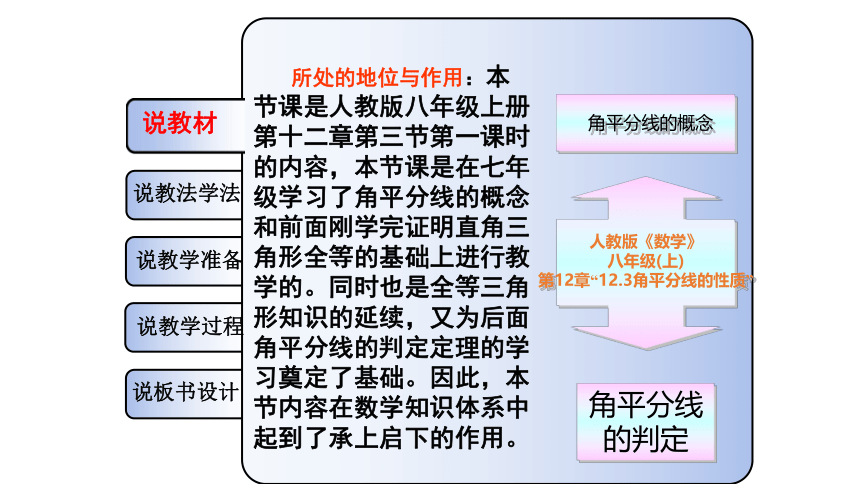
所处的地位与作用:本节课是人教版八年级上册第十二章第三节第一课时的内容,本节课是在七年级学习了角平分线的概念和前面刚学完证明直角三角形全等的基础上进行教学的。同时也是全等三角形知识的延续,又为后面角平分线的判定定理的学习奠定了基础。因此,本节内容在数学知识体系中起到了承上启下的作用。
说教学准备
说教学过程
说板书设计
说教材
角平分线的概念
人教版《数学》
八年级(上)
第12章“12.3角平分线的性质”
角平分线的判定
说教法学法
学情分析
八年级学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强引导。
说教学准备
说教学过程
说板书设计
说教材
说教法学法
教学目标
知识与技能:掌握用尺规作已知角的平分线的方法;理解角的平分线的性质并能初步运用。
过程与方法:让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用数学知识解决问题的能力。
情感与态度:充分利用多媒体教学优势,培养学生探究问题的兴趣,增强解决问题的信心,获得解决问题的成功体验,激发学生应用数学的热情。
说教学准备
说教学过程
说板书设计
说教材
说教法学法
教学重点:(1)掌握角平分线的尺规作图。(2)理解角的平分线的性质并能初步运用。
教学难点:(1)角平分线的尺规作图。(2)角平分线的性质的探究过程。
说教学准备
说教学过程
说板书设计
说教材
说教学准备
说教学过程
说板书设计
说教材
说教法学法
依据学生认知规律,遵循“学生为主体,教师为主导,教学活动为主线”的指导思想,本节课我采用引导发现法、主动探究法、讲授教学法。指导学生“动手操作,合作交流,自主探究”。鼓励学生多思、多说、多练,坚持师生间的多向交流。
说教学过程
说板书设计
说教材
说教法学法
说教学准备
自制平分角的仪器,
多媒体课件。
说板书设计
说教材
说教法学法
说教学准备
说教学过程
创设情境
激发兴趣
观察猜想
尝试作图
合作探究
归纳性质
归纳小结
反思提高
运用性质
解决问题
布置作业
学以致用
(一). 创设情景,激发兴趣
出示自制的平分角的仪器,提问:同学们,猜猜这是什么?学生会直观的回答是四边形。追问:(1)在这个四边形中你发现哪些等量?(2)如何把这个四边形转化成三角形?这些问题学生都能轻松的解答,然后告诉学生我这个模型有一个神秘的用途,在黑板上任意画一个角,用此模型找出角平分线,学生恍然大悟。
·
·
·
·
设计意图:利用自制仪器,通过问题激发学生的求知欲。用旧知引出课题,同时为角平分线的尺规作图埋下伏笔。
(1)引导学生通过观察上一环节中角平分线的由来,设计问题:不用量角器,借助这个仪器的原理,如何作已知角的角平分线?引出“尺规作图”的概念,并对概念进行简单的讲解。
(2)鼓励学生尝试作图,因为这是一个难点,学生只有少部分能够完成。
(3)我在黑板上演示并详细讲解后,询问:对刚才你自己的作图还满意吗?激发学生再次作图的主动性。
(二)观察猜想,尝试作图
(二)观察猜想,尝试作图
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC,则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
角平分线的画法:
设计意图:让学生通过观察、
猜想、实践、再实践的过程,
体验到成功的喜悦,同时突破
本节课的一个难点。培养学生学习
数学的严谨性。
(1)让学生表演角平分线,提问:角平分线上这个小王同学要到角两边去逛逛,他怎样走才能使路线最短?学生很容易根据垂线段最短得出最短路径。
(2)让小王同学和两边的同学用彩带拉出垂线段,让大家猜猜这两条彩带的数量关系怎么样?通过直观的观察猜想它们的数量相等,在让表演的3位同学把彩带重叠,使学生发现确实相等。
(3)换另一个同学再次尝试,结束后让学生猜想角平分线上有什么性质,并进行验证。
(4)我再用多媒体课件呈现角平分线的性质及其几何语言,同时展示出论证的过程。
(三)合作探究,归纳性质
(三)合作探究,归纳性质
猜想:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.求证:PD=PE.
(书写证明过程)
设计意图:以情景呈现任务,以任务驱动
探索,注重让学生参与知识的形成过程,体现
学生为主体,使学生的思维由形象直观过渡到
抽象的逻辑推理,达到突破教学难点的目的。
例 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
(四)运用性质,解决问题
设计意图:让学生把所学知识及时巩固消化。
◆本节课我们主要研究了什么内容?
◆你有哪些收获?
◆还有哪些疑问?
(五)归纳小结 反思提高
设计意图:让学生按照上述的模式进行小结,
培养学生:学习——总结——反思的良好习惯。
(六)作业布置,学以致用
(1)必做题:课本第51页的习题1.2.3;
(2)选做题:课本第52页的习题6.7
设计意图:作业分层处理,为不同程度的学生
提供更为广阔的探求空间,完成本节课的教学目标。
通过作业,内化知识,检验学生掌握知识的情况,
发现和弥补教与学中的遗漏和不足。
12·3角平分线的性质
尺规作图
角平分线性质的证明
范例讲解
板书设计
设计意图:清晰再现本课的重点难点,有利于
学生不断地加强和深化对知识的掌握。
谢谢聆听
角平分线的性质
(第1课时)
说教法学法
所处的地位与作用:本节课是人教版八年级上册第十二章第三节第一课时的内容,本节课是在七年级学习了角平分线的概念和前面刚学完证明直角三角形全等的基础上进行教学的。同时也是全等三角形知识的延续,又为后面角平分线的判定定理的学习奠定了基础。因此,本节内容在数学知识体系中起到了承上启下的作用。
说教学准备
说教学过程
说板书设计
说教材
角平分线的概念
人教版《数学》
八年级(上)
第12章“12.3角平分线的性质”
角平分线的判定
说教法学法
学情分析
八年级学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强引导。
说教学准备
说教学过程
说板书设计
说教材
说教法学法
教学目标
知识与技能:掌握用尺规作已知角的平分线的方法;理解角的平分线的性质并能初步运用。
过程与方法:让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用数学知识解决问题的能力。
情感与态度:充分利用多媒体教学优势,培养学生探究问题的兴趣,增强解决问题的信心,获得解决问题的成功体验,激发学生应用数学的热情。
说教学准备
说教学过程
说板书设计
说教材
说教法学法
教学重点:(1)掌握角平分线的尺规作图。(2)理解角的平分线的性质并能初步运用。
教学难点:(1)角平分线的尺规作图。(2)角平分线的性质的探究过程。
说教学准备
说教学过程
说板书设计
说教材
说教学准备
说教学过程
说板书设计
说教材
说教法学法
依据学生认知规律,遵循“学生为主体,教师为主导,教学活动为主线”的指导思想,本节课我采用引导发现法、主动探究法、讲授教学法。指导学生“动手操作,合作交流,自主探究”。鼓励学生多思、多说、多练,坚持师生间的多向交流。
说教学过程
说板书设计
说教材
说教法学法
说教学准备
自制平分角的仪器,
多媒体课件。
说板书设计
说教材
说教法学法
说教学准备
说教学过程
创设情境
激发兴趣
观察猜想
尝试作图
合作探究
归纳性质
归纳小结
反思提高
运用性质
解决问题
布置作业
学以致用
(一). 创设情景,激发兴趣
出示自制的平分角的仪器,提问:同学们,猜猜这是什么?学生会直观的回答是四边形。追问:(1)在这个四边形中你发现哪些等量?(2)如何把这个四边形转化成三角形?这些问题学生都能轻松的解答,然后告诉学生我这个模型有一个神秘的用途,在黑板上任意画一个角,用此模型找出角平分线,学生恍然大悟。
·
·
·
·
设计意图:利用自制仪器,通过问题激发学生的求知欲。用旧知引出课题,同时为角平分线的尺规作图埋下伏笔。
(1)引导学生通过观察上一环节中角平分线的由来,设计问题:不用量角器,借助这个仪器的原理,如何作已知角的角平分线?引出“尺规作图”的概念,并对概念进行简单的讲解。
(2)鼓励学生尝试作图,因为这是一个难点,学生只有少部分能够完成。
(3)我在黑板上演示并详细讲解后,询问:对刚才你自己的作图还满意吗?激发学生再次作图的主动性。
(二)观察猜想,尝试作图
(二)观察猜想,尝试作图
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC,则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
角平分线的画法:
设计意图:让学生通过观察、
猜想、实践、再实践的过程,
体验到成功的喜悦,同时突破
本节课的一个难点。培养学生学习
数学的严谨性。
(1)让学生表演角平分线,提问:角平分线上这个小王同学要到角两边去逛逛,他怎样走才能使路线最短?学生很容易根据垂线段最短得出最短路径。
(2)让小王同学和两边的同学用彩带拉出垂线段,让大家猜猜这两条彩带的数量关系怎么样?通过直观的观察猜想它们的数量相等,在让表演的3位同学把彩带重叠,使学生发现确实相等。
(3)换另一个同学再次尝试,结束后让学生猜想角平分线上有什么性质,并进行验证。
(4)我再用多媒体课件呈现角平分线的性质及其几何语言,同时展示出论证的过程。
(三)合作探究,归纳性质
(三)合作探究,归纳性质
猜想:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.求证:PD=PE.
(书写证明过程)
设计意图:以情景呈现任务,以任务驱动
探索,注重让学生参与知识的形成过程,体现
学生为主体,使学生的思维由形象直观过渡到
抽象的逻辑推理,达到突破教学难点的目的。
例 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
(四)运用性质,解决问题
设计意图:让学生把所学知识及时巩固消化。
◆本节课我们主要研究了什么内容?
◆你有哪些收获?
◆还有哪些疑问?
(五)归纳小结 反思提高
设计意图:让学生按照上述的模式进行小结,
培养学生:学习——总结——反思的良好习惯。
(六)作业布置,学以致用
(1)必做题:课本第51页的习题1.2.3;
(2)选做题:课本第52页的习题6.7
设计意图:作业分层处理,为不同程度的学生
提供更为广阔的探求空间,完成本节课的教学目标。
通过作业,内化知识,检验学生掌握知识的情况,
发现和弥补教与学中的遗漏和不足。
12·3角平分线的性质
尺规作图
角平分线性质的证明
范例讲解
板书设计
设计意图:清晰再现本课的重点难点,有利于
学生不断地加强和深化对知识的掌握。
谢谢聆听
