物理人教版(2019)选择性必修第一册4.1光的折射(共24张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册4.1光的折射(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-24 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
第4章 光
4.1 光的折射
学习目标
1.物理观念:理解折射率的物理意义。
2.科学思维:理解光的折射定律,并能用来解释和计算有关的问题。
3.科学探究:掌握测定玻璃折射率的实验,会解决与实验相关的问题。
引入
筷子“折断” 是不是光的反射呢?
如果不是,那么这属于哪种现象呢?
山峦在湖泊中的倒影是光的反射现象
加水
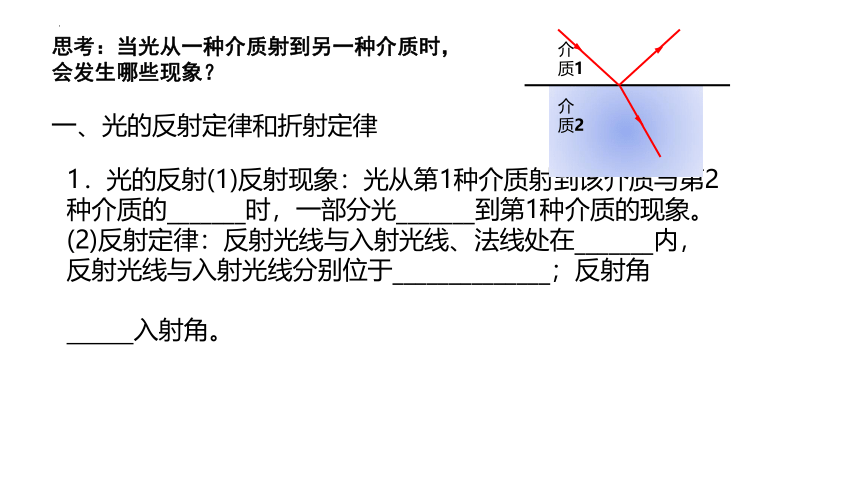
一、光的反射定律和折射定律
1.光的反射(1)反射现象:光从第1种介质射到该介质与第2种介质的_______时,一部分光_______到第1种介质的现象。(2)反射定律:反射光线与入射光线、法线处在_______内,反射光线与入射光线分别位于______________;反射角
入射角。
思考:当光从一种介质射到另一种介质时,会发生哪些现象?
介质1
介质2
2.光的折射(1)折射现象:光从第1种介质射到该介质与第2种介质的_______时,一部分光_______第2种介质的现象。
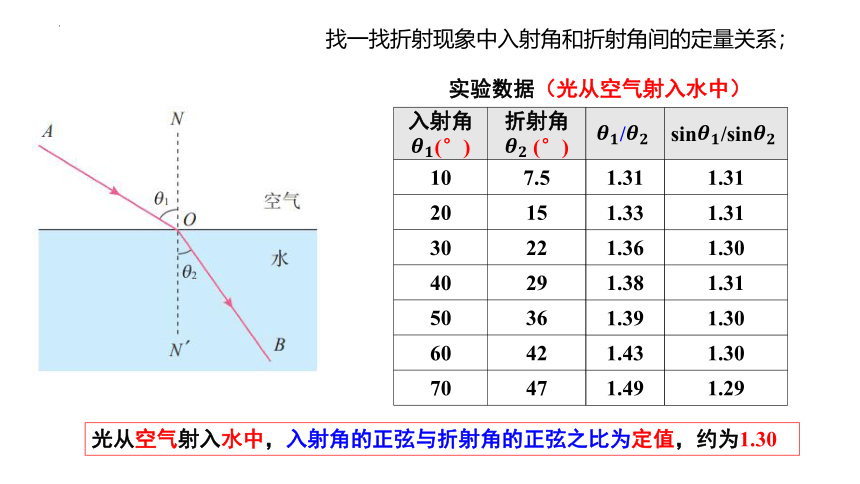
实验数据(光从空气射入水中)
入射角(°) 折射角(°)
10 7.5
20 15
30 22
40 29
50 36
60 42
70 47
/
1.31
1.33
1.36
1.38
1.39
1.43
1.49
找一找折射现象中入射角和折射角间的定量关系;
sin/sin
1.31
1.31
1.30
1.31
1.30
1.30
1.29
光从空气射入水中,入射角的正弦与折射角的正弦之比为定值,约为1.30
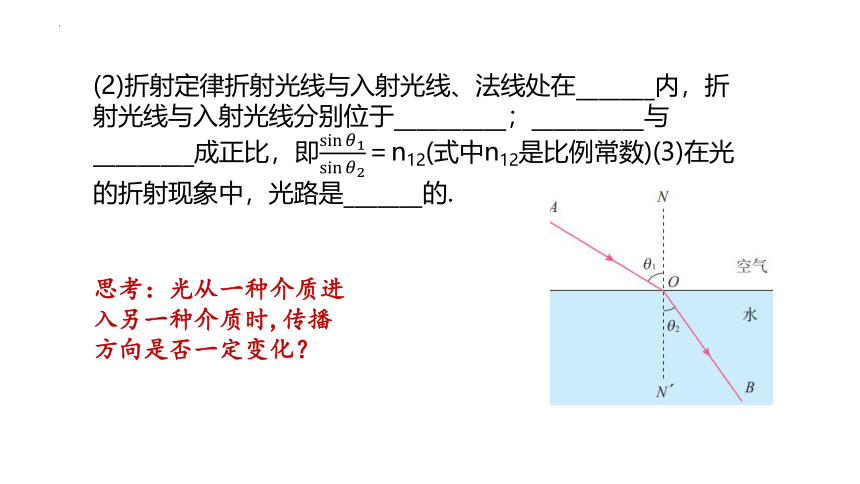
(2)折射定律折射光线与入射光线、法线处在_______内,折射光线与入射光线分别位于__________;__________与_________成正比,即=n12(式中n12是比例常数)(3)在光的折射现象中,光路是_______的.
思考:光从一种介质进入另一种介质时,传播方向是否一定变化?
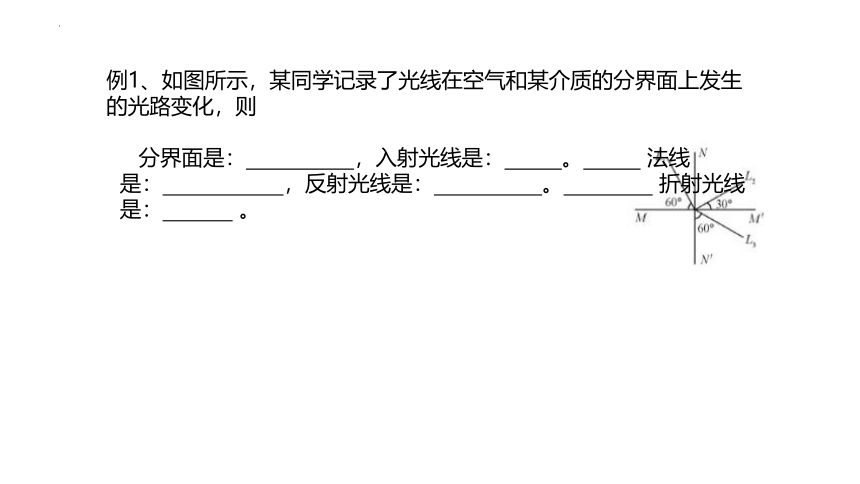
例1、如图所示,某同学记录了光线在空气和某介质的分界面上发生的光路变化,则
分界面是: ,入射光线是: 。 法线是: ,反射光线是: 。 折射光线是: 。
二、 折射率
1.定义:
光从真空射入某种介质发生折射时,______________与______________之比,叫作这种介质的绝对折射率,简称折射率,即n= 。 2.折射率与光速的关系
某种介质的折射率,等于光在_______中的传播速度c与光在这种介质中的传播速度v之比,即n= 。
3.理解
(1)由于c>v,故任何介质的折射率n都_______(填“大于”“小于”或“等于”)1。
(2)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值。光以相同入射角从真空射入玻璃和水中,大体上画出其折射光线。
(3)折射率反映介质对光的偏折作用,n越 光线偏折越 。
例2、一束光由空气射入某介质,当入射光线和界面的夹角为30°时,折射光线恰好与反射光线垂直,则光在该介质中的传播速度是( )
A. B.
C. D.
D
例3、两束平行的细激光束垂直于半圆柱形玻璃的平面射入,如图所示.已知其中一束光沿直线穿过玻璃,它的入射点是O,另一束光的入射点是A,穿过玻璃后两条光线交于P点.已知玻璃半圆截面的半径为R,OA=,OP=R.求玻璃的折射率.
例4:边长为d的正方体透明介质置于真空中,其横截面ABCD如图所示。有两束平行光Ⅰ、Ⅱ分别从上表面的A点和AB的中点沿与水平方向成30°角同时斜射入介质中,两种光在界面上折射后恰好相交于正方体底面的C点。已知真空中光速为c,求:
(1)介质对光Ⅰ、Ⅱ的折射率;
(2)光Ⅰ、Ⅱ到达C点的时间差。
1.实验原理
用插针法确定光路,找出跟入射光线相对应的折射光线,用量角器测出入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率n= .
2.实验器材
玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、三角板(或直尺)、铅笔.
3.实验步骤
(1)如图所示,将白纸用图钉钉在平木板上.
(2)在白纸上画出一条直线aa′作为界面(线),
过aa′上的一点O画出界面的法线NN′,并
画一条线段AO作为入射光线.
三、测玻璃砖的折射率
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′.
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像.再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置.
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O ′B与bb′交于O′,直线O ′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向.
(6)连接OO ′,入射角θ1=∠AON,折射角θ2=∠O ′ON ′,用量角器量出入射角和折射角.
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角.
4、数据处理(1)方法一:平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测 的平均值,即为玻璃砖的折射率。
(2)方法二:图象法
以 值为横坐标、 值为纵坐标,建立直角坐标系,如右图所示.描数据点,过数据点连线得一条过原点的直线.求解图线斜率k,则k= ,故玻璃砖折射率n= 。
在找到入射光线和折射光线以后,以入射点O为 ,以任意长为半径画圆,分别与AO交于C点,OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图所示.由于sinθ1= ,sinθ2= ,且CO=DO,所以折射率n1= = 。
(3)方法三:作图法
例5、如图1所示,某同学在“测定玻璃的折射率”的实验中,先将白纸平铺在木板上并用图钉固定,玻璃砖平放在白纸上,然后在白纸上确定玻璃砖的界面aa′和bb′,O为直线AO与aa′的交点。在直线OA上竖直地插上P1、P2两枚大头针。
(1)该同学接下来要完成的必要步骤有____。A.插上大头针P3,使P3仅挡住P2的像B.插上大头针P3,使P3挡住P1的像和P2的像C.插上大头针P4,使P4仅挡住P3D.插上大头针P4,使P4挡住P3和P1、P2的像
(2)过P3、P4作直线交bb′于O′,过O′作垂直于bb′的直线NN′,连接OO′。测量图1中角α和β的大小。则玻璃砖的折射率n=____ 。
(3)如图2所示,该同学在实验中将玻璃砖界面aa′和bb′的间距画得过宽。若其他操作正确,则折射率的测量值____准确值(选填“大于”“小于”或“等于”)。
(4)另一位同学准确地画好玻璃砖的界面aa′和bb′后,实验过程中不慎将玻璃砖向下平移了一些,如图3所示,而实验的其他操作均正确,则折射率的测量值____ 准确值(选填“大于”“小于”或“等于”)。
本课小结
1.折射定律
折射光线、入射光线、法线在同一平面内。折射光线和入射光线分居法线两侧。入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
2.理解(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
(3)当入射角增大时,折射角也随着增大。
(4)在光的折射现象中,光路是可逆的。
3.测量玻璃的折射率:插针法
巩固练习
1.如图所示,一玻璃柱体的横截面为半圆形,细的单色光束从空气射向柱体的O点(半圆的圆心),产生反射光束1和透射光束2。已知光从空气射向玻璃时入射角的正弦与折射角的正弦的比值为,入射角为45°(相应的折射角为24°)。现保持入射光不变,将半圆柱绕通过O点垂直于图面轴线顺时针转过15°,如图中虚线所示。则( )
A.光束1转过15° B.光束1转过30°
C.光束2转过的角度小于15° D.光束2转过的角度大于15°
2、一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距d/4 。求油的折射率和光在油中传播的速度。
3、真空中有一半径为R=5 cm、球心为O、质量均匀分布的玻璃球,其球心O的横截面如图所示.一单色光束SA从真空以入射角θ1在玻璃球表面的A点射入玻璃球,又从玻璃球表面的B点射出.已知∠AOB=120°,该光在玻璃中的折射率为,光在真空中的传播速度c=3×108 m/s,求:
(1)入射角θ1的值;
(2)该光束在玻璃球中的传播时间t
第4章 光
4.1 光的折射
学习目标
1.物理观念:理解折射率的物理意义。
2.科学思维:理解光的折射定律,并能用来解释和计算有关的问题。
3.科学探究:掌握测定玻璃折射率的实验,会解决与实验相关的问题。
引入
筷子“折断” 是不是光的反射呢?
如果不是,那么这属于哪种现象呢?
山峦在湖泊中的倒影是光的反射现象
加水
一、光的反射定律和折射定律
1.光的反射(1)反射现象:光从第1种介质射到该介质与第2种介质的_______时,一部分光_______到第1种介质的现象。(2)反射定律:反射光线与入射光线、法线处在_______内,反射光线与入射光线分别位于______________;反射角
入射角。
思考:当光从一种介质射到另一种介质时,会发生哪些现象?
介质1
介质2
2.光的折射(1)折射现象:光从第1种介质射到该介质与第2种介质的_______时,一部分光_______第2种介质的现象。
实验数据(光从空气射入水中)
入射角(°) 折射角(°)
10 7.5
20 15
30 22
40 29
50 36
60 42
70 47
/
1.31
1.33
1.36
1.38
1.39
1.43
1.49
找一找折射现象中入射角和折射角间的定量关系;
sin/sin
1.31
1.31
1.30
1.31
1.30
1.30
1.29
光从空气射入水中,入射角的正弦与折射角的正弦之比为定值,约为1.30
(2)折射定律折射光线与入射光线、法线处在_______内,折射光线与入射光线分别位于__________;__________与_________成正比,即=n12(式中n12是比例常数)(3)在光的折射现象中,光路是_______的.
思考:光从一种介质进入另一种介质时,传播方向是否一定变化?
例1、如图所示,某同学记录了光线在空气和某介质的分界面上发生的光路变化,则
分界面是: ,入射光线是: 。 法线是: ,反射光线是: 。 折射光线是: 。
二、 折射率
1.定义:
光从真空射入某种介质发生折射时,______________与______________之比,叫作这种介质的绝对折射率,简称折射率,即n= 。 2.折射率与光速的关系
某种介质的折射率,等于光在_______中的传播速度c与光在这种介质中的传播速度v之比,即n= 。
3.理解
(1)由于c>v,故任何介质的折射率n都_______(填“大于”“小于”或“等于”)1。
(2)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值。光以相同入射角从真空射入玻璃和水中,大体上画出其折射光线。
(3)折射率反映介质对光的偏折作用,n越 光线偏折越 。
例2、一束光由空气射入某介质,当入射光线和界面的夹角为30°时,折射光线恰好与反射光线垂直,则光在该介质中的传播速度是( )
A. B.
C. D.
D
例3、两束平行的细激光束垂直于半圆柱形玻璃的平面射入,如图所示.已知其中一束光沿直线穿过玻璃,它的入射点是O,另一束光的入射点是A,穿过玻璃后两条光线交于P点.已知玻璃半圆截面的半径为R,OA=,OP=R.求玻璃的折射率.
例4:边长为d的正方体透明介质置于真空中,其横截面ABCD如图所示。有两束平行光Ⅰ、Ⅱ分别从上表面的A点和AB的中点沿与水平方向成30°角同时斜射入介质中,两种光在界面上折射后恰好相交于正方体底面的C点。已知真空中光速为c,求:
(1)介质对光Ⅰ、Ⅱ的折射率;
(2)光Ⅰ、Ⅱ到达C点的时间差。
1.实验原理
用插针法确定光路,找出跟入射光线相对应的折射光线,用量角器测出入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率n= .
2.实验器材
玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、三角板(或直尺)、铅笔.
3.实验步骤
(1)如图所示,将白纸用图钉钉在平木板上.
(2)在白纸上画出一条直线aa′作为界面(线),
过aa′上的一点O画出界面的法线NN′,并
画一条线段AO作为入射光线.
三、测玻璃砖的折射率
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′.
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像.再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置.
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O ′B与bb′交于O′,直线O ′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向.
(6)连接OO ′,入射角θ1=∠AON,折射角θ2=∠O ′ON ′,用量角器量出入射角和折射角.
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角.
4、数据处理(1)方法一:平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测 的平均值,即为玻璃砖的折射率。
(2)方法二:图象法
以 值为横坐标、 值为纵坐标,建立直角坐标系,如右图所示.描数据点,过数据点连线得一条过原点的直线.求解图线斜率k,则k= ,故玻璃砖折射率n= 。
在找到入射光线和折射光线以后,以入射点O为 ,以任意长为半径画圆,分别与AO交于C点,OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图所示.由于sinθ1= ,sinθ2= ,且CO=DO,所以折射率n1= = 。
(3)方法三:作图法
例5、如图1所示,某同学在“测定玻璃的折射率”的实验中,先将白纸平铺在木板上并用图钉固定,玻璃砖平放在白纸上,然后在白纸上确定玻璃砖的界面aa′和bb′,O为直线AO与aa′的交点。在直线OA上竖直地插上P1、P2两枚大头针。
(1)该同学接下来要完成的必要步骤有____。A.插上大头针P3,使P3仅挡住P2的像B.插上大头针P3,使P3挡住P1的像和P2的像C.插上大头针P4,使P4仅挡住P3D.插上大头针P4,使P4挡住P3和P1、P2的像
(2)过P3、P4作直线交bb′于O′,过O′作垂直于bb′的直线NN′,连接OO′。测量图1中角α和β的大小。则玻璃砖的折射率n=____ 。
(3)如图2所示,该同学在实验中将玻璃砖界面aa′和bb′的间距画得过宽。若其他操作正确,则折射率的测量值____准确值(选填“大于”“小于”或“等于”)。
(4)另一位同学准确地画好玻璃砖的界面aa′和bb′后,实验过程中不慎将玻璃砖向下平移了一些,如图3所示,而实验的其他操作均正确,则折射率的测量值____ 准确值(选填“大于”“小于”或“等于”)。
本课小结
1.折射定律
折射光线、入射光线、法线在同一平面内。折射光线和入射光线分居法线两侧。入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
2.理解(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
(3)当入射角增大时,折射角也随着增大。
(4)在光的折射现象中,光路是可逆的。
3.测量玻璃的折射率:插针法
巩固练习
1.如图所示,一玻璃柱体的横截面为半圆形,细的单色光束从空气射向柱体的O点(半圆的圆心),产生反射光束1和透射光束2。已知光从空气射向玻璃时入射角的正弦与折射角的正弦的比值为,入射角为45°(相应的折射角为24°)。现保持入射光不变,将半圆柱绕通过O点垂直于图面轴线顺时针转过15°,如图中虚线所示。则( )
A.光束1转过15° B.光束1转过30°
C.光束2转过的角度小于15° D.光束2转过的角度大于15°
2、一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距d/4 。求油的折射率和光在油中传播的速度。
3、真空中有一半径为R=5 cm、球心为O、质量均匀分布的玻璃球,其球心O的横截面如图所示.一单色光束SA从真空以入射角θ1在玻璃球表面的A点射入玻璃球,又从玻璃球表面的B点射出.已知∠AOB=120°,该光在玻璃中的折射率为,光在真空中的传播速度c=3×108 m/s,求:
(1)入射角θ1的值;
(2)该光束在玻璃球中的传播时间t
