第4章 几何图形初步 单元复习题(含解析) 2023-2024学年上学期山西省人教版数学七年级上册
文档属性
| 名称 | 第4章 几何图形初步 单元复习题(含解析) 2023-2024学年上学期山西省人教版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览


文档简介
第4章 几何图形初步
一、单选题
1.(2023下·山西运城·七年级山西省运城市实验中学校考期末)朵朵在学习整式的除法时,遇到这样一个问题:如图所示,三个大小相同的球恰好放在一个圆柱形盒子里,三个球的体积之和占整个盒子容积的几分之几?
她不知道从何下手,去请教老师.老师让她先思考以下问题:
如图所示,三个半径大小均为2cm的球恰好放在一个圆柱形盒子里.三个球的体积和为多少?整个盒子容积是多少?三个球的体积占整个盒子容积的几分之几?
三个半径大小均为5cm的球恰好放在一个圆柱形盒子里,三个球的体积占整个盒子容积的几分之几?三个球的半径为10cm呢?
朵朵通过具体数值的运算发现:球半径的大小,没有影响体积占盒子容积的比例,自然联想到将球的半径设为cm,再用关于的代数式分别表示出三个球的体积之和与盒子容积,进而通过单项式除以单项式的运算解决问题.
以上解决问题的过程中,用到的数学思想是( )
A.分类思想 B.转化思想 C.归纳思想 D.方程思想
2.(2023上·山西太原·七年级统考期末)如图是某个几何体的平面展开图,该几何体可能是( )
A. B. C. D.
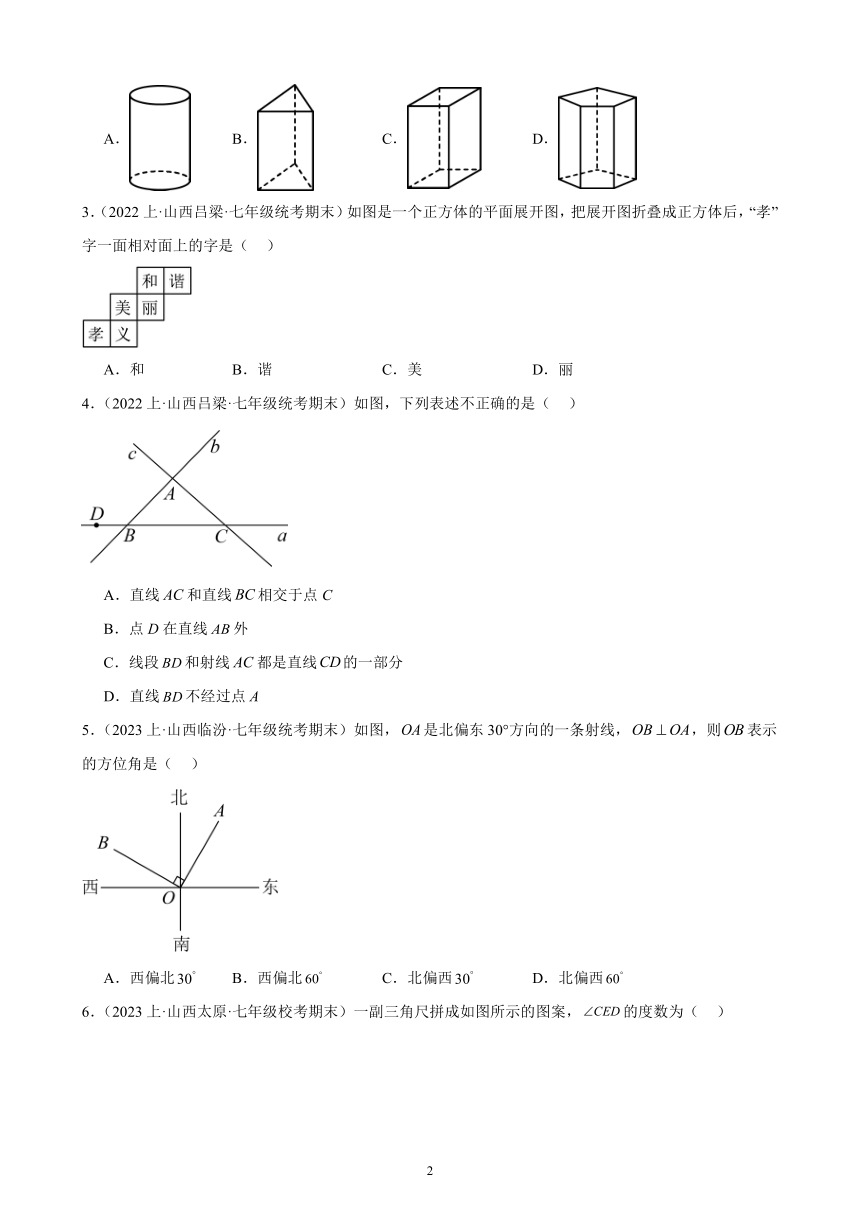
3.(2022上·山西吕梁·七年级统考期末)如图是一个正方体的平面展开图,把展开图折叠成正方体后,“孝”字一面相对面上的字是( )
A.和 B.谐 C.美 D.丽
4.(2022上·山西吕梁·七年级统考期末)如图,下列表述不正确的是( )
A.直线和直线相交于点C
B.点D在直线外
C.线段和射线都是直线的一部分
D.直线不经过点A
5.(2023上·山西临汾·七年级统考期末)如图,是北偏东30°方向的一条射线,,则表示的方位角是( )
A.西偏北 B.西偏北 C.北偏西 D.北偏西
6.(2023上·山西太原·七年级校考期末)一副三角尺拼成如图所示的图案,的度数为( )
A. B. C. D.
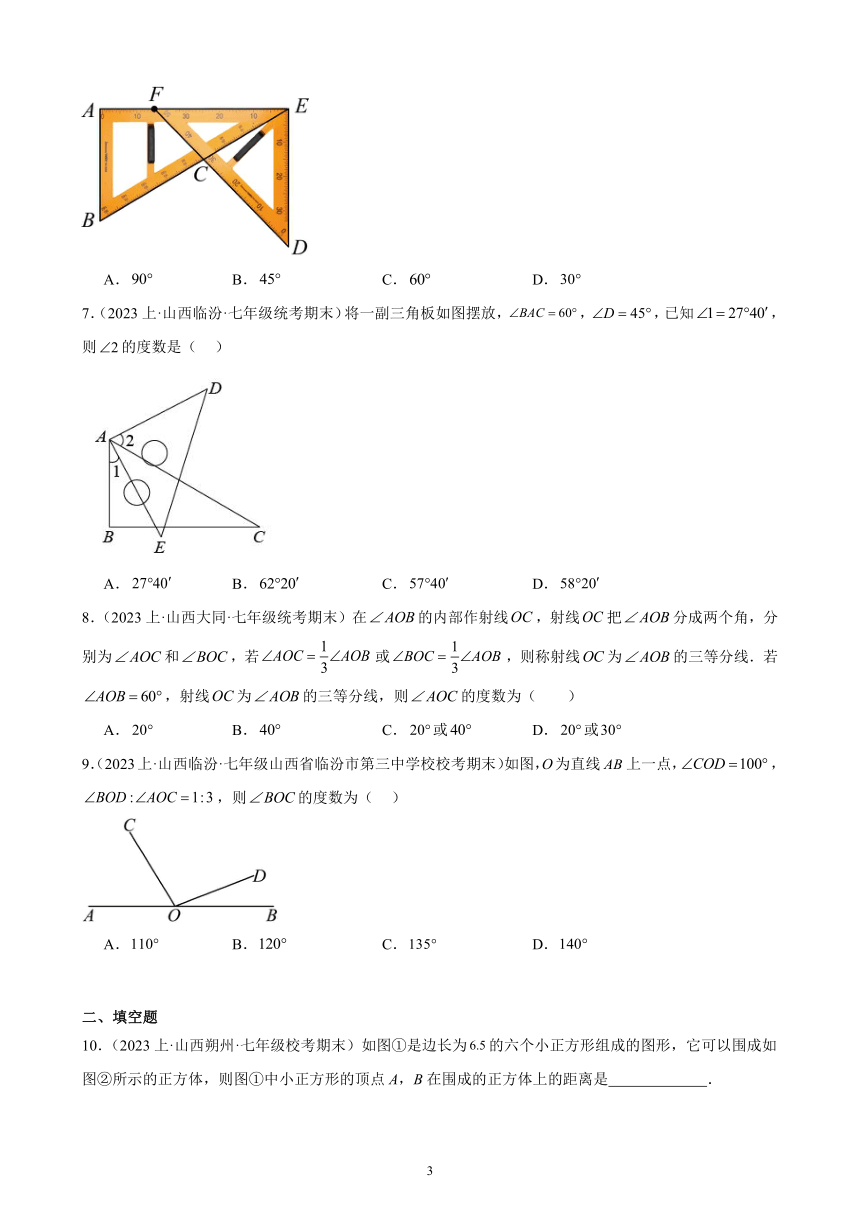
7.(2023上·山西临汾·七年级统考期末)将一副三角板如图摆放,,,已知,则的度数是( )
A. B. C. D.
8.(2023上·山西大同·七年级统考期末)在的内部作射线,射线把分成两个角,分别为和,若或,则称射线为的三等分线.若,射线为的三等分线,则的度数为( )
A. B. C.或 D.或
9.(2023上·山西临汾·七年级山西省临汾市第三中学校校考期末)如图,O为直线上一点,,,则的度数为( )
A. B. C. D.
二、填空题
10.(2023上·山西朔州·七年级校考期末)如图①是边长为的六个小正方形组成的图形,它可以围成如图②所示的正方体,则图①中小正方形的顶点A,B在围成的正方体上的距离是 .
11.(2023上·山西阳泉·七年级统考期末)如图,点A,B,C,D,E在线段MN上,则图中共有 条线段.
12.(2023上·山西运城·七年级统考期末)已知线段,点D是线段的中点,直线上有一点C,且,则线段 .
13.(2023上·山西大同·七年级统考期末)金秋十月,大同公园色彩斑斓.小明同学捡到一片沿直线被折断了的银杏叶(如图),他发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
14.(2023上·山西晋中·七年级校考期末)如图,在灯塔处观测到轮船A位于北偏东的方向,同时轮船B在南偏东的方向,那么 .
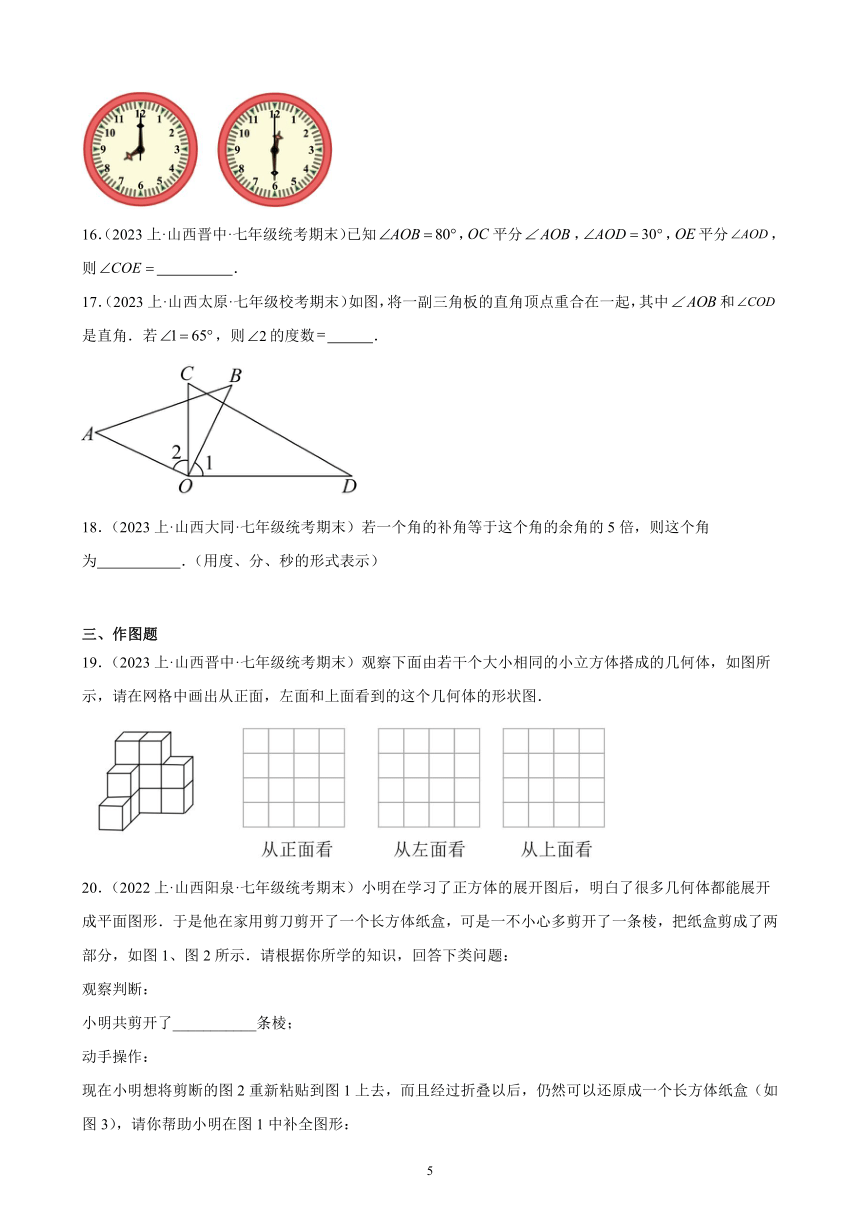
15.(2023上·山西晋城·七年级统考期末)小明利用星期天搞社会调查活动,早晨8:00出发,中午12:30到家,小明到家时时针和分针夹角的度数是 .
16.(2023上·山西晋中·七年级统考期末)已知,平分,,平分,则 .
17.(2023上·山西太原·七年级校考期末)如图,将一副三角板的直角顶点重合在一起,其中和是直角.若,则的度数 .
18.(2023上·山西大同·七年级统考期末)若一个角的补角等于这个角的余角的5倍,则这个角为 .(用度、分、秒的形式表示)
三、作图题
19.(2023上·山西晋中·七年级统考期末)观察下面由若干个大小相同的小立方体搭成的几何体,如图所示,请在网格中画出从正面,左面和上面看到的这个几何体的形状图.
20.(2022上·山西阳泉·七年级统考期末)小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下类问题:
观察判断:
小明共剪开了___________条棱;
动手操作:
现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形:
解决问题:
经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是,求这个纸盒的体积.
21.(2023上·山西晋中·七年级校考期末)已知线段,求作:线段,使.(尺规作图,保留痕迹.)
22.(2023上·山西太原·七年级统考期末)如图,已知不在同一条直线上的三点,,.按下面的要求用尺规作图(不必写出结论):连接,,作射线;在射线上取一点,使.
23.(2023上·山西晋中·七年级校考期末)补全解题过程.
如图所示点是线段的中点,点在线段上,且.若,求线段的长.
解:∵点是线段的中点,(已知)
∴.
∵,(已知)
∴_________.
∵在线段上,,(已知)
∴_________.
∴_________.
∴__________________.
24.(2022上·山西吕梁·七年级统考期末)如图,已知线段a,b.射线.
实践与操作:在射线上作线段,.(要求:尺规作图,保留作图痕迹,不写作法).
推理与计算:若线段的中点是点D,线段的中点是点E.请在上图中标出点D,E.当,时,求线段的长度.
四、计算题
25.(2023上·山西晋中·七年级统考期末)4月23日是世界读书日,新华书店举办“书香”图书展,已知《汉语成语大词典》和《世界历史》两本书的标价总和为150元,《汉语成语大词典》按标价的五折出售,《世界历史》按标价的六折出售.
(1)小明花80元买了这两本书,问这两本书的标价各为多少元?
(2)学校组织向“同心小学”献爱心的捐赠活动,小明决定将这两本书进行捐赠,于是他找来一个长方体纸盒包装,量得纸盒的长、宽、高分别为,计算此包装盒的表面积.
(3)礼品店内包装纸每平方米10元,且包装的手工费1元,而他只有3元,那么对该纸盒进行包装,他的钱够吗?
26.(2023上·山西临汾·七年级统考期末)主题式学习:数形规律探究学习
(1)发现规律,猜想说理.
............
以此类推,我们发现的和与第一个数、最后一个数及数的个数有关.
如果,我们设
则
我们可以看出此等式的右边是若干个的和,
∴_________.
则_______.
(2)运用规律,计算表达.
①求_____________.
②若,则__________.
③某校为庆祝2023年元旦,活跃学生文化生活,举行歌咏比赛.七年级(9)班获得第一名,该班学生列队以“单击掌”形式(每两个学生击掌一次)祝贺获奖;活动结束后该班同学又互赠“元旦祝福语”.如果该班有名同学,则共击掌_____________次,共赠送祝福语___________条.
(3)迁移规律,解决问题.
①如图,“北京——广州”航线上有A、B、C、D、E、F、G、H8个城市,如果每两个城市都要互通航班,那么这条航线上一共需要开通_____架航班.
②如图,在的方格中,横线和竖线上的线段共有___________条.
③2022年足球世界杯在卡塔尔举行(如图是足球世界杯奖杯“大力神杯”和卡塔尔世界杯会徽、吉祥物),共有32支国家足球队参赛.比赛分小组赛、1/8决赛、1/4决赛、半决赛、三四名决赛、决赛六个阶段进行.32支球队平均分成8个进行小组循环赛(小组内每两支球队举行一场比赛);每小组前两名球队进入1/8决赛,然后实行淘汰赛,胜者进入1/4决赛......请你计算2022年足球世界杯共进行多少场比赛?
五、问答题
27.(2023上·山西太原·七年级校考期末)如图,直线上有A,B,,四个点,,,.
(1)线段 ______
(2)动点P,Q分别从A点,点同时出发,点P沿线段以/秒的速度,向右运动,到达点后立即按原速向A点返回;点Q沿线段以/秒的速度,向左运动;P点再次到达A点时,两点同时停止运动.设运动时间为t(单位:秒)
①求P,Q两点第一次相遇时,运动时间t的值;
②求P,Q两点第二次相遇时,与点A的距离.
28.(2023上·山西晋城·七年级统考期末)如图,点是线段的中点,点是线段的中点,且.
(1)图中共有___________条线段;
(2)求的长;
(3)若点在直线上,且,直接写出的长.
29.(2022上·山西吕梁·七年级统考期末)综合与探究
问题情境:
数学活动课上,老师以直线上一点O为端点作射线,,,,使平分,平分,若,求的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当时,则的度数为______;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺角的顶点放在点O处,即当时,请你在图3中求的度数;
数学思考:
(3)请你在图1中,求的度数)(用含有的式子表示).
30.(2023上·山西运城·七年级统考期末)如图,将直角三角板的直角顶点O放在直线上,射线平分.
(1)如图(1),若,求的度数;
(2)如图(2)若,求的度数;
(3)将直角三角板绕顶点O按逆时针方向旋转一周,在旋转过程中:当时,求的度数.
31.(2023上·山西晋中·七年级统考期末)综合与探究
问题情境:
数学活动课上,老师带领学生用一副直角三角尺进行“玩转三角尺”的探究活动.
问题实践:
(1)老师将三角尺和三角尺按如图1所示摆放在直线上,边落在直线上,,,,则 ;
操作探究:
(2)奋进小组将图1中三角尺绕点逆时针旋转进行探究,当边首次落在直线上时停止旋转,若以每秒的速度旋转,设三角尺旋转时间为秒,提出下列问题,请你帮忙解答.
_____秒,边落在边上;
当边平分时, _______秒;
深度探究:
(3)如图2,腾飞小组受奋进小组的启发继续进行探究:在三角尺绕点以每秒的速度逆时针旋转的同时,将三角尺也绕点以每秒的速度顺时针旋转,当三角尺的边首次落在直线上时停止旋转,同时三角尺也停止旋转,求为何值时,.
32.(2023上·山西大同·七年级统考期末)综合与探究
阅读材料:如图是七年级上册课本135页的探究,将纸片折叠使与重合,是折痕,此时与重合,所以,射线是的平分线.
知识初探:
(1)如图1,已知是锐角内部的一条射线,将折叠,使射线和射线重合,为折痕,将折叠,使射线和射线重合,为折痕,若,,求的度数.
类比探究:
(2)如图2,在长方形纸片中,点E,F分别在边,上,连接,将折叠,使点A落在点G处,平分,若,求的度数(用含的式子表示).
参考答案:
1.C
【分析】本题考查的是数学归纳思想的运用,理解归纳思想的应用是解本题的关键.
【详解】解:设球的半径为,
根据题意得:一个球的体积,
圆柱体盒子容积,
∴三个球的体积与整个盒子容积之比为,
∴球半径的大小,没有影响体积占盒子容积的比例,
这种解决问题的过程中,用到的数学思想是归纳思想.
故选C.
2.D
【分析】通过展开图的面数,展开图的各个面的形状进行判断即可.
【详解】解:从展开图可知,该几何体有七个面,两个五边形的底面,五个长方形的侧面,
因此该几何体是五棱柱,
故选:D.
【点睛】本题考查棱柱的展开与折叠,掌握棱柱展开图的特征是正确判断的关键.
3.D
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:这是一个正方体的平面展开图,共有六个面,
其中有“和”字的一面相对面上的字是“义”,
“孝”字的一面相对面上的字是“丽”,
“谐”字的一面相对面上的字是“美”.
故选:D.
【点睛】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
4.C
【分析】根据直线、射线与线段的定义,结合图形解答.
【详解】解:A、直线和直线相交于点C,此选项正确,故不符合题意;
B、点D在直线外,此选项正确,故不符合题意;
C、线段是直线的一部分,射线不是直线的一部分,此选项错误,故符合题意;
D、直线不经过点A,此选项正确,故不符合题意,
故选:C.
【点睛】本题考查了直线、射线、线段,解题的关键是掌握直线、射线、线段的定义,注意它们之间的区别与联系.
5.D
【分析】根据可知,由题意是北偏东方向的一条射线,可得,再根据方位角的定义即可得出答案.
【详解】如图,对图形进行标注,
∵,
∴,
∴,
即射线的方位角是北偏西.
故选.
【点睛】本题主要考查方位角的定义以及余角的计算方法,熟练掌握方位角的基础知识是解决本题的关键.
6.C
【分析】由题意得,,从而可求的度数.
【详解】一副三角尺拼成如图所示的图案,
,,
∴,
故选:C.
【点睛】本题考查了角的计算,结合图形分析清楚各角之间的关系是解题的关键.
7.C
【分析】根据三角尺中角的大小关系计算即可,注意的换算.
【详解】解:,
,
,
,
故选:C.
【点睛】本题考查了三角板中角度的计算,掌握角度制的换算是解题关键.
8.C
【分析】根据题意得出或,再根据角之间的数量关系,得出,综合即可得出答案.
【详解】解:∵,射线为的三等分线.
∴或,
∴,
∴的度数为或.
故选:C.
【点睛】本题考查了角度的计算,理解题意,分类讨论是解本题的关键.
9.B
【分析】利用角的和差关系和平角的定义,先求出,再得结论.
【详解】解:∵O为直线上一点,,
∴,
又∵,
∴,
∴,
故选:B.
【点睛】本题主要考查了角的计算,掌握平角的定义和角的和差关系是解决本题的关键.
10.
【分析】将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到之间的距离.
【详解】解:将图1折成正方体后点A和点B为同一条棱的两个端点,故此.
故答案为:.
【点睛】本题主要考查的是展开图折成几何体,判断出点A和点B在几何体中的位置关系是解题的关键.
11.21
【分析】根据两点确定一条线段进行求解即可.
【详解】解:由题意得,图中的线段有,,,,,,
∴一共有21条线段,
故答案为:21.
【点睛】本题主要考出来数线段的条数,熟知两点确定一条线段是解题的关键.
12.6或18/18或6
【分析】根据线段中点的性质,可得的长,设,根据线段的和差列出方程解答便可.
【详解】解:∵,点D是线段的中点,
∴,
设,则,
当C点在B、D之间时,
∵,
∴,
解得,
∴;
当C点在的延长线上时,
∵,
∴,
解得,
∴;
故答案为:6或18.
【点睛】本题考查了两点间的距离,以及线段的中点,利用线段的和差是解题关键,要分类讨论以防遗漏.
13.两点之间,线段最短
【分析】根据两点之间,线段最短即可求解.
【详解】解:剩下的银杏叶的一边是线段,原先是曲线,
剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是:两点之间,线段最短,
故答案为:两点之间,线段最短.
【点睛】题目主要考查两点之间,线段最短,理解题意是解题关键.
14./107度
【分析】根据题意可得,,从而即可解答.
【详解】
如图,∵在灯塔处观测到轮船A位于北偏东的方向,
∴,
∵轮船B在灯塔的南偏东的方向,
∴,
∴.
故答案为:
【点睛】此题主要考查了方向角,根据题意找出图中对应角的度数是解题的关键.
15./165度
【分析】时针在钟面上每分钟转,分针每分钟转,钟表上12:30时,时针与分针的夹角可以看成时针转过12时,分针在数字6上,由此进行计算即可得到答案.
【详解】解:时针在钟面上每分钟转,分针每分钟转,
钟表上12:30时,时针与分针的夹角可以看成时针转过12时,分针在数字6上,
钟表12个数字,每相邻两个数字之间的夹角为,
12:30时针与分针的夹角为:,
小明到家时时针和分针夹角的度数是,
故答案为:.
【点睛】本题考查的是钟表表盘与角度相关的特征,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为,在钟表问题中,常利用时针与分针转动的度数关系:分针每转动时针转动,并且利用起点时针和分针的位置关系建立角的图形.
16.或
【分析】根据角平分线的定义求出的度数,再分两种情况求出.
【详解】解: ∵,平分,
∴,
∵,平分,
∴,
当在内部时,如图,
;
当在外部时,如图,
,
故答案为:或
【点睛】此题考查了角平分线的定义,几何图形中求角的度数,正确掌握角平分线的定义是解题的关键.
17./65度
【分析】根据等角(或同角)的余角相等,得到,即可得到答案.
【详解】解:,
,
,
,
,
故答案为:.
【点睛】本题考查了余角的概念,解题关键是掌握等角的余角相等.
18.
【分析】利用题中的关系“一个角的补角等于这个角的余角的5倍”作为相等关系列方程求解即可.
【详解】解:设这个角为x,则它的补角为,余角为,由题意得:
,
解得:.
即这个角的度数为.
故答案为:.
【点睛】本题主要考查了余角和补角的定义,一元一次方程的应用.解此题的关键是能准确的从题中找出各个量之间的数量关系,找出等量关系列方程,从而计算出结果.互为余角的两角的和为,互为补角的两角之和为.
19.见解析
【分析】画出从从正面,左面和上面看到的这个几何体的形状图即可.
【详解】解:如图所示,
【点睛】此题考查了从不同方向看几何体,准确画出看到的形状是解题的关键.
20.观察判断:8;动手操作:见解析;解决问题:这个长方体纸盒的体积为:.
【分析】观察判断:根据图形回答即可;
动手操作:根据长方体的展开图的情况可知有四种情况;
解决问题:设高为,则正方形边长为,根据棱长的和是列出方程,据此可求出长、宽、高,因而求出长方体纸盒的体积.
【详解】解:观察判断:
小明总共剪开了8条棱;
故答案为:8;
动手操作:如图,有四种情况:
;
解决问题:因为长方体纸盒的底面是一个正方形,
所以设高为,则正方形边长为.
因为长方体纸盒所有棱长的和是,
所以,
解得,
所以这个长方体纸盒的体积为:.
【点睛】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
21.见解析
【分析】先作射线,再以A为圆心,以线段a的长为半径画弧交射线于B,再以B为圆心,以线段c的长为半径画弧交射线于C,再以C为圆心,以线段b的长为半径画弧交线段于D,则线段即为所求.
【详解】解:如图,为所作.
【点睛】本题主要考查了线段的尺规作图,正确理清线段之间的关系是解题的关键.
22.见解析
【分析】根据直线、射线、线段的定义画图,再在射线上取,则.
【详解】解:如图,即为所求.
【点睛】本题考查作图复杂作图、直线、射线、线段,熟练掌握直线、射线、线段的定义以及作一条线段等于已知线段的方法是解答本题的关键.
23.,,,,
【分析】根据线段中点的性质得出,进而根据题意得出,得出,根据,即可求解.
【详解】解:∵点是线段的中点,(已知)
∴.
∵,(已知)
∴.
∵在线段上,,(已知)
∴.
∴.
∴.
故答案为:,,,,.
【点睛】本题考查了线段中点的性质,线段和差的计算,数形结合是解题的关键.
24.,图见解析
【分析】实践与操作:在射线上分别顺次截取线段,即可.
推理与计算:先求出长,再根据线段的中点求出和长,即可求出答案;
【详解】实践与操作:如图,线段即为所求线段.
推理与计算:
解:由作图可知,,,,
因为点D是的中点,点E是的中点,
所以,,
所以.
【点睛】本题主要考查两点间的距离,掌握中点的定义是解题的关键.
25.(1)《汉语成语大词典》的标价是100元,《中华上下五千年》的标价是50元;
(2)这个包装盒的表面积是;
(3)对礼品盒进行包装,她的钱不够.
【分析】(1)设《汉语成语大词典》的标价是元,则《中华上下五千年》的标价是元,依题意列出一元一次方程,求解即可;
(2)要求长方体的表面积,根据“长方体的表面积长宽长高宽高”,代入数值,进行解答即可;
(3)由包装纸每平方米10元,且包装手工费1元求出对礼品盒进行包装所需的费用,与3元钱进行比较即可.
【详解】(1)解:设《汉语成语大词典》的标价是元,则《中华上下五千年》的标价是元,
根据题意得:,解得:,
(元),
答:《汉语成语大词典》的标价是100元,《中华上下五千年》的标价是50元;
(2)解:,
答:这个包装盒的表面积是;
(3)解:∵包装纸每平方米10元,且包装手工费1元,
∴对礼品盒进行包装所需的费用是:(元),
∵,
∴对礼品盒进行包装,她的钱不够.
【点睛】本题考查了一元一次方程的应用以及代数式求值,掌握长方体的表面积公式是解题的关键.
26.(1),
(2)①5047;②100;③,
(3)①90;②135;③
【分析】(1)根据题目中的规律即可求解;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律得出方程,解方程即可求解;③根据规律即可求解;
(3)①10个城市每两个城市都要互通航班,据此即可求解;②分别计算横向和竖向的线段条数,即可求解;③利用分类的方法可求得2022年足球世界杯共进行多少场比赛.
【详解】(1)解:.
则.
故答案为:,;
(2)解:①.
②∵,
∴,解得或(舍去),
则.
③如果该班有名同学,则共击掌次,共赠送祝福语条.
故答案为:①5047;②100;③,;
(3)解:①如图,“北京——广州”航线上有A、B、C、D、E、F、G、H8个城市,如果每两个城市都要互通航班,10个城市一共需要开通架航班;
②横线上的线段有条,竖线上的线段有条,
则横线和竖线上的线段共有条;
③32支比赛分为8个小组,每个小组4支球队,共有场比赛,
16强分成8组对阵,共有8场比赛,
8强分成4组对阵,共有4场比赛,
4强分成2组对阵,共有2场比赛,
决赛有2场比赛,
故共有场比赛.
故答案为:①90;②135;③64.
【点睛】本题考查了探索规律,线段的计数,线段的计数时应注重分类讨论的方法计数,做到不遗漏,不重复,利用规律解决问题.
27.(1)
(2)8、20
【分析】(1)先根据题意算出,再根据即可解答,掌握线段的和差倍分是解题的关键;
(2)①根据P,Q两点第一次相遇时,P,Q两点所走的路程之和是的长列方程求解即可;②根据P,Q两点第二次相遇时,P 点所走的路程与的差以及Q所走的路程与的差相等列方程即可求解;根据线段的和差列出方程是解答本题的关键.
【详解】(1)解:∵,,.
∴,
∴.
故线段的长为.
(2)解:①P,Q两点第一次相遇时,点P运动的路程为,点Q运动的路程为t,
根据题意可知:P,Q两点第一次相遇时,P,Q两点所走的路程之和是,即,解得: 秒
故P,Q两点第一次相遇时,运动时间t的值是8秒;
②P,Q两点第二次相遇时,点P运动的路程为,点Q运动的路程为t,
由(1)得 ,
根据题意可知:P,Q两点第二次相遇时,P 点所走的路程与的差以及Q所走的路程与的差相等,即:,解得: 秒,
∴,
∴.
故P,Q两点第二次相遇时,与点A的距离是.
28.(1)6
(2)6.75cm
(3)3.75cm或9.75cm
【分析】(1)根据线段的定义找出线段即可;
(2)根据线段的中点和两条线段的和的定义,求出结果;
(3)由于点在直线上的具体位置不确定,故应分点在点的左边和点在点的右边两种情况分别求解.
【详解】(1)图中有6条线段,它们是线段,,,,,.
故答案为:6.
(2)点是线段的中点,,
,
点是线段的中点,
,
(3)当点在点的左边,,
,
当点在点的右边,,
故答案为:3.75cm或9.75cm.
【点睛】本题主要考查了两点间的距离,线段中点的定义和线段和差的定义,熟练掌握各线段之间的和差以及倍数关系是解本题的关键.
29.(1);(2);(3)
【分析】(1)求得,利用角平分线的定义得,据此求解即可;
(2)求得,利用角平分线的定义得,据此求解即可;
(3)求得,利用角平分线的定义得求解即可.
【详解】解:(1)因为,所以,
因为平分,平分,
所以,,
所以
;
故答案为:;
(2)因为,所以,
因为平分,ON平分,
所以,,
所以
;
(3)因为,所以,
因为平分,平分,
所以,,
所以
.
【点睛】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
30.(1)
(2)
(3)的度数为或
【分析】(1)为直角三角板,所以,又因为,所以;
(2)平分,所以,又因为,根据,得到,,即可得到;
(3)分类讨论,当OQ在直线AB上方时并做图;当OQ在直线AB下方时并做图,根据图形信息和条件信息进行列式计算即可.
【详解】(1)∵ 为直角三角板,
∴ ,
∵,,
∴ ;
(2)∵平分,
∴ ,
∵ ,
设,则,
∵ ,
∴,,
∴ ,,
由(1)得,
∴ ,
(3)①如图,当在直线上方时,
∵ ,∴ ,
∵ 平分,∴,
∵ ,∴,
②如图,当在直线下方时,
∵ ,∴ ,
∵ 平分,∴ ,
∵ ,∴ ;
综上所述:的度数为或.
【点睛】本题主要考查了角平分线的定义及角的计算,熟练掌握角平分线的定义及角的计算的方法进行求解是解决本题的关键.
31.(1)
(2)5;10.5
(3)3或4.5秒
【分析】(1)由计算即可得到答案;
(2)由(1)得,,当边落在边上,刚好旋转的度数为的度数,
因此;
先求出旋转的角度,再根据时间=路程÷速度,进行计算即可求解;
(3)分两种情况:边与边相遇前;边与边相遇后,列方程进行计算即可得到
答案.
【详解】(1)解:,,,
,
故答案为:;
(2)解:由(1)得,,
当边落在边上,刚好旋转的度数为的度数,
三角尺绕点逆时针旋转的速度为以每秒,
,
故答案为:5;
当边平分时,画出图如图所示,
边平分,
,
旋转角度为,
,
故答案为:10.5;
(3)解:由(1)可知,两个三角尺旋转前,,边旋转的角度为,边旋转的角度为,
边与边相遇前,可得:,
解得:;
边与边相遇后,可得:,
解得:,
为3或4.5秒时,.
【点睛】本题考查了几何图形中角度的计算、与角平分线有关的角度的计算、旋转的性质、一元一次方程的应用,熟练掌握以上知识点,采用分类讨论的思想解题,是解题的关键.
32.(1)
(2)
【分析】(1)根据折叠的性质得出,,求解即可;
(2)由折叠知,再由角平分线及邻补角得出,结合图形,进行等量代换求解即可.
【详解】(1)解:由折叠知,
同理:
∴
(2)由折叠知,
又∵
∴
∵平分
∴
∵
∴
∴
∴.
【点睛】题目主要考查角平分线及角度的计算,结合图形,找准各角之间的关系是解题关键.
一、单选题
1.(2023下·山西运城·七年级山西省运城市实验中学校考期末)朵朵在学习整式的除法时,遇到这样一个问题:如图所示,三个大小相同的球恰好放在一个圆柱形盒子里,三个球的体积之和占整个盒子容积的几分之几?
她不知道从何下手,去请教老师.老师让她先思考以下问题:
如图所示,三个半径大小均为2cm的球恰好放在一个圆柱形盒子里.三个球的体积和为多少?整个盒子容积是多少?三个球的体积占整个盒子容积的几分之几?
三个半径大小均为5cm的球恰好放在一个圆柱形盒子里,三个球的体积占整个盒子容积的几分之几?三个球的半径为10cm呢?
朵朵通过具体数值的运算发现:球半径的大小,没有影响体积占盒子容积的比例,自然联想到将球的半径设为cm,再用关于的代数式分别表示出三个球的体积之和与盒子容积,进而通过单项式除以单项式的运算解决问题.
以上解决问题的过程中,用到的数学思想是( )
A.分类思想 B.转化思想 C.归纳思想 D.方程思想
2.(2023上·山西太原·七年级统考期末)如图是某个几何体的平面展开图,该几何体可能是( )
A. B. C. D.
3.(2022上·山西吕梁·七年级统考期末)如图是一个正方体的平面展开图,把展开图折叠成正方体后,“孝”字一面相对面上的字是( )
A.和 B.谐 C.美 D.丽
4.(2022上·山西吕梁·七年级统考期末)如图,下列表述不正确的是( )
A.直线和直线相交于点C
B.点D在直线外
C.线段和射线都是直线的一部分
D.直线不经过点A
5.(2023上·山西临汾·七年级统考期末)如图,是北偏东30°方向的一条射线,,则表示的方位角是( )
A.西偏北 B.西偏北 C.北偏西 D.北偏西
6.(2023上·山西太原·七年级校考期末)一副三角尺拼成如图所示的图案,的度数为( )
A. B. C. D.
7.(2023上·山西临汾·七年级统考期末)将一副三角板如图摆放,,,已知,则的度数是( )
A. B. C. D.
8.(2023上·山西大同·七年级统考期末)在的内部作射线,射线把分成两个角,分别为和,若或,则称射线为的三等分线.若,射线为的三等分线,则的度数为( )
A. B. C.或 D.或
9.(2023上·山西临汾·七年级山西省临汾市第三中学校校考期末)如图,O为直线上一点,,,则的度数为( )
A. B. C. D.
二、填空题
10.(2023上·山西朔州·七年级校考期末)如图①是边长为的六个小正方形组成的图形,它可以围成如图②所示的正方体,则图①中小正方形的顶点A,B在围成的正方体上的距离是 .
11.(2023上·山西阳泉·七年级统考期末)如图,点A,B,C,D,E在线段MN上,则图中共有 条线段.
12.(2023上·山西运城·七年级统考期末)已知线段,点D是线段的中点,直线上有一点C,且,则线段 .
13.(2023上·山西大同·七年级统考期末)金秋十月,大同公园色彩斑斓.小明同学捡到一片沿直线被折断了的银杏叶(如图),他发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
14.(2023上·山西晋中·七年级校考期末)如图,在灯塔处观测到轮船A位于北偏东的方向,同时轮船B在南偏东的方向,那么 .
15.(2023上·山西晋城·七年级统考期末)小明利用星期天搞社会调查活动,早晨8:00出发,中午12:30到家,小明到家时时针和分针夹角的度数是 .
16.(2023上·山西晋中·七年级统考期末)已知,平分,,平分,则 .
17.(2023上·山西太原·七年级校考期末)如图,将一副三角板的直角顶点重合在一起,其中和是直角.若,则的度数 .
18.(2023上·山西大同·七年级统考期末)若一个角的补角等于这个角的余角的5倍,则这个角为 .(用度、分、秒的形式表示)
三、作图题
19.(2023上·山西晋中·七年级统考期末)观察下面由若干个大小相同的小立方体搭成的几何体,如图所示,请在网格中画出从正面,左面和上面看到的这个几何体的形状图.
20.(2022上·山西阳泉·七年级统考期末)小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下类问题:
观察判断:
小明共剪开了___________条棱;
动手操作:
现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形:
解决问题:
经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是,求这个纸盒的体积.
21.(2023上·山西晋中·七年级校考期末)已知线段,求作:线段,使.(尺规作图,保留痕迹.)
22.(2023上·山西太原·七年级统考期末)如图,已知不在同一条直线上的三点,,.按下面的要求用尺规作图(不必写出结论):连接,,作射线;在射线上取一点,使.
23.(2023上·山西晋中·七年级校考期末)补全解题过程.
如图所示点是线段的中点,点在线段上,且.若,求线段的长.
解:∵点是线段的中点,(已知)
∴.
∵,(已知)
∴_________.
∵在线段上,,(已知)
∴_________.
∴_________.
∴__________________.
24.(2022上·山西吕梁·七年级统考期末)如图,已知线段a,b.射线.
实践与操作:在射线上作线段,.(要求:尺规作图,保留作图痕迹,不写作法).
推理与计算:若线段的中点是点D,线段的中点是点E.请在上图中标出点D,E.当,时,求线段的长度.
四、计算题
25.(2023上·山西晋中·七年级统考期末)4月23日是世界读书日,新华书店举办“书香”图书展,已知《汉语成语大词典》和《世界历史》两本书的标价总和为150元,《汉语成语大词典》按标价的五折出售,《世界历史》按标价的六折出售.
(1)小明花80元买了这两本书,问这两本书的标价各为多少元?
(2)学校组织向“同心小学”献爱心的捐赠活动,小明决定将这两本书进行捐赠,于是他找来一个长方体纸盒包装,量得纸盒的长、宽、高分别为,计算此包装盒的表面积.
(3)礼品店内包装纸每平方米10元,且包装的手工费1元,而他只有3元,那么对该纸盒进行包装,他的钱够吗?
26.(2023上·山西临汾·七年级统考期末)主题式学习:数形规律探究学习
(1)发现规律,猜想说理.
............
以此类推,我们发现的和与第一个数、最后一个数及数的个数有关.
如果,我们设
则
我们可以看出此等式的右边是若干个的和,
∴_________.
则_______.
(2)运用规律,计算表达.
①求_____________.
②若,则__________.
③某校为庆祝2023年元旦,活跃学生文化生活,举行歌咏比赛.七年级(9)班获得第一名,该班学生列队以“单击掌”形式(每两个学生击掌一次)祝贺获奖;活动结束后该班同学又互赠“元旦祝福语”.如果该班有名同学,则共击掌_____________次,共赠送祝福语___________条.
(3)迁移规律,解决问题.
①如图,“北京——广州”航线上有A、B、C、D、E、F、G、H8个城市,如果每两个城市都要互通航班,那么这条航线上一共需要开通_____架航班.
②如图,在的方格中,横线和竖线上的线段共有___________条.
③2022年足球世界杯在卡塔尔举行(如图是足球世界杯奖杯“大力神杯”和卡塔尔世界杯会徽、吉祥物),共有32支国家足球队参赛.比赛分小组赛、1/8决赛、1/4决赛、半决赛、三四名决赛、决赛六个阶段进行.32支球队平均分成8个进行小组循环赛(小组内每两支球队举行一场比赛);每小组前两名球队进入1/8决赛,然后实行淘汰赛,胜者进入1/4决赛......请你计算2022年足球世界杯共进行多少场比赛?
五、问答题
27.(2023上·山西太原·七年级校考期末)如图,直线上有A,B,,四个点,,,.
(1)线段 ______
(2)动点P,Q分别从A点,点同时出发,点P沿线段以/秒的速度,向右运动,到达点后立即按原速向A点返回;点Q沿线段以/秒的速度,向左运动;P点再次到达A点时,两点同时停止运动.设运动时间为t(单位:秒)
①求P,Q两点第一次相遇时,运动时间t的值;
②求P,Q两点第二次相遇时,与点A的距离.
28.(2023上·山西晋城·七年级统考期末)如图,点是线段的中点,点是线段的中点,且.
(1)图中共有___________条线段;
(2)求的长;
(3)若点在直线上,且,直接写出的长.
29.(2022上·山西吕梁·七年级统考期末)综合与探究
问题情境:
数学活动课上,老师以直线上一点O为端点作射线,,,,使平分,平分,若,求的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当时,则的度数为______;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺角的顶点放在点O处,即当时,请你在图3中求的度数;
数学思考:
(3)请你在图1中,求的度数)(用含有的式子表示).
30.(2023上·山西运城·七年级统考期末)如图,将直角三角板的直角顶点O放在直线上,射线平分.
(1)如图(1),若,求的度数;
(2)如图(2)若,求的度数;
(3)将直角三角板绕顶点O按逆时针方向旋转一周,在旋转过程中:当时,求的度数.
31.(2023上·山西晋中·七年级统考期末)综合与探究
问题情境:
数学活动课上,老师带领学生用一副直角三角尺进行“玩转三角尺”的探究活动.
问题实践:
(1)老师将三角尺和三角尺按如图1所示摆放在直线上,边落在直线上,,,,则 ;
操作探究:
(2)奋进小组将图1中三角尺绕点逆时针旋转进行探究,当边首次落在直线上时停止旋转,若以每秒的速度旋转,设三角尺旋转时间为秒,提出下列问题,请你帮忙解答.
_____秒,边落在边上;
当边平分时, _______秒;
深度探究:
(3)如图2,腾飞小组受奋进小组的启发继续进行探究:在三角尺绕点以每秒的速度逆时针旋转的同时,将三角尺也绕点以每秒的速度顺时针旋转,当三角尺的边首次落在直线上时停止旋转,同时三角尺也停止旋转,求为何值时,.
32.(2023上·山西大同·七年级统考期末)综合与探究
阅读材料:如图是七年级上册课本135页的探究,将纸片折叠使与重合,是折痕,此时与重合,所以,射线是的平分线.
知识初探:
(1)如图1,已知是锐角内部的一条射线,将折叠,使射线和射线重合,为折痕,将折叠,使射线和射线重合,为折痕,若,,求的度数.
类比探究:
(2)如图2,在长方形纸片中,点E,F分别在边,上,连接,将折叠,使点A落在点G处,平分,若,求的度数(用含的式子表示).
参考答案:
1.C
【分析】本题考查的是数学归纳思想的运用,理解归纳思想的应用是解本题的关键.
【详解】解:设球的半径为,
根据题意得:一个球的体积,
圆柱体盒子容积,
∴三个球的体积与整个盒子容积之比为,
∴球半径的大小,没有影响体积占盒子容积的比例,
这种解决问题的过程中,用到的数学思想是归纳思想.
故选C.
2.D
【分析】通过展开图的面数,展开图的各个面的形状进行判断即可.
【详解】解:从展开图可知,该几何体有七个面,两个五边形的底面,五个长方形的侧面,
因此该几何体是五棱柱,
故选:D.
【点睛】本题考查棱柱的展开与折叠,掌握棱柱展开图的特征是正确判断的关键.
3.D
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:这是一个正方体的平面展开图,共有六个面,
其中有“和”字的一面相对面上的字是“义”,
“孝”字的一面相对面上的字是“丽”,
“谐”字的一面相对面上的字是“美”.
故选:D.
【点睛】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
4.C
【分析】根据直线、射线与线段的定义,结合图形解答.
【详解】解:A、直线和直线相交于点C,此选项正确,故不符合题意;
B、点D在直线外,此选项正确,故不符合题意;
C、线段是直线的一部分,射线不是直线的一部分,此选项错误,故符合题意;
D、直线不经过点A,此选项正确,故不符合题意,
故选:C.
【点睛】本题考查了直线、射线、线段,解题的关键是掌握直线、射线、线段的定义,注意它们之间的区别与联系.
5.D
【分析】根据可知,由题意是北偏东方向的一条射线,可得,再根据方位角的定义即可得出答案.
【详解】如图,对图形进行标注,
∵,
∴,
∴,
即射线的方位角是北偏西.
故选.
【点睛】本题主要考查方位角的定义以及余角的计算方法,熟练掌握方位角的基础知识是解决本题的关键.
6.C
【分析】由题意得,,从而可求的度数.
【详解】一副三角尺拼成如图所示的图案,
,,
∴,
故选:C.
【点睛】本题考查了角的计算,结合图形分析清楚各角之间的关系是解题的关键.
7.C
【分析】根据三角尺中角的大小关系计算即可,注意的换算.
【详解】解:,
,
,
,
故选:C.
【点睛】本题考查了三角板中角度的计算,掌握角度制的换算是解题关键.
8.C
【分析】根据题意得出或,再根据角之间的数量关系,得出,综合即可得出答案.
【详解】解:∵,射线为的三等分线.
∴或,
∴,
∴的度数为或.
故选:C.
【点睛】本题考查了角度的计算,理解题意,分类讨论是解本题的关键.
9.B
【分析】利用角的和差关系和平角的定义,先求出,再得结论.
【详解】解:∵O为直线上一点,,
∴,
又∵,
∴,
∴,
故选:B.
【点睛】本题主要考查了角的计算,掌握平角的定义和角的和差关系是解决本题的关键.
10.
【分析】将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到之间的距离.
【详解】解:将图1折成正方体后点A和点B为同一条棱的两个端点,故此.
故答案为:.
【点睛】本题主要考查的是展开图折成几何体,判断出点A和点B在几何体中的位置关系是解题的关键.
11.21
【分析】根据两点确定一条线段进行求解即可.
【详解】解:由题意得,图中的线段有,,,,,,
∴一共有21条线段,
故答案为:21.
【点睛】本题主要考出来数线段的条数,熟知两点确定一条线段是解题的关键.
12.6或18/18或6
【分析】根据线段中点的性质,可得的长,设,根据线段的和差列出方程解答便可.
【详解】解:∵,点D是线段的中点,
∴,
设,则,
当C点在B、D之间时,
∵,
∴,
解得,
∴;
当C点在的延长线上时,
∵,
∴,
解得,
∴;
故答案为:6或18.
【点睛】本题考查了两点间的距离,以及线段的中点,利用线段的和差是解题关键,要分类讨论以防遗漏.
13.两点之间,线段最短
【分析】根据两点之间,线段最短即可求解.
【详解】解:剩下的银杏叶的一边是线段,原先是曲线,
剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是:两点之间,线段最短,
故答案为:两点之间,线段最短.
【点睛】题目主要考查两点之间,线段最短,理解题意是解题关键.
14./107度
【分析】根据题意可得,,从而即可解答.
【详解】
如图,∵在灯塔处观测到轮船A位于北偏东的方向,
∴,
∵轮船B在灯塔的南偏东的方向,
∴,
∴.
故答案为:
【点睛】此题主要考查了方向角,根据题意找出图中对应角的度数是解题的关键.
15./165度
【分析】时针在钟面上每分钟转,分针每分钟转,钟表上12:30时,时针与分针的夹角可以看成时针转过12时,分针在数字6上,由此进行计算即可得到答案.
【详解】解:时针在钟面上每分钟转,分针每分钟转,
钟表上12:30时,时针与分针的夹角可以看成时针转过12时,分针在数字6上,
钟表12个数字,每相邻两个数字之间的夹角为,
12:30时针与分针的夹角为:,
小明到家时时针和分针夹角的度数是,
故答案为:.
【点睛】本题考查的是钟表表盘与角度相关的特征,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为,在钟表问题中,常利用时针与分针转动的度数关系:分针每转动时针转动,并且利用起点时针和分针的位置关系建立角的图形.
16.或
【分析】根据角平分线的定义求出的度数,再分两种情况求出.
【详解】解: ∵,平分,
∴,
∵,平分,
∴,
当在内部时,如图,
;
当在外部时,如图,
,
故答案为:或
【点睛】此题考查了角平分线的定义,几何图形中求角的度数,正确掌握角平分线的定义是解题的关键.
17./65度
【分析】根据等角(或同角)的余角相等,得到,即可得到答案.
【详解】解:,
,
,
,
,
故答案为:.
【点睛】本题考查了余角的概念,解题关键是掌握等角的余角相等.
18.
【分析】利用题中的关系“一个角的补角等于这个角的余角的5倍”作为相等关系列方程求解即可.
【详解】解:设这个角为x,则它的补角为,余角为,由题意得:
,
解得:.
即这个角的度数为.
故答案为:.
【点睛】本题主要考查了余角和补角的定义,一元一次方程的应用.解此题的关键是能准确的从题中找出各个量之间的数量关系,找出等量关系列方程,从而计算出结果.互为余角的两角的和为,互为补角的两角之和为.
19.见解析
【分析】画出从从正面,左面和上面看到的这个几何体的形状图即可.
【详解】解:如图所示,
【点睛】此题考查了从不同方向看几何体,准确画出看到的形状是解题的关键.
20.观察判断:8;动手操作:见解析;解决问题:这个长方体纸盒的体积为:.
【分析】观察判断:根据图形回答即可;
动手操作:根据长方体的展开图的情况可知有四种情况;
解决问题:设高为,则正方形边长为,根据棱长的和是列出方程,据此可求出长、宽、高,因而求出长方体纸盒的体积.
【详解】解:观察判断:
小明总共剪开了8条棱;
故答案为:8;
动手操作:如图,有四种情况:
;
解决问题:因为长方体纸盒的底面是一个正方形,
所以设高为,则正方形边长为.
因为长方体纸盒所有棱长的和是,
所以,
解得,
所以这个长方体纸盒的体积为:.
【点睛】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
21.见解析
【分析】先作射线,再以A为圆心,以线段a的长为半径画弧交射线于B,再以B为圆心,以线段c的长为半径画弧交射线于C,再以C为圆心,以线段b的长为半径画弧交线段于D,则线段即为所求.
【详解】解:如图,为所作.
【点睛】本题主要考查了线段的尺规作图,正确理清线段之间的关系是解题的关键.
22.见解析
【分析】根据直线、射线、线段的定义画图,再在射线上取,则.
【详解】解:如图,即为所求.
【点睛】本题考查作图复杂作图、直线、射线、线段,熟练掌握直线、射线、线段的定义以及作一条线段等于已知线段的方法是解答本题的关键.
23.,,,,
【分析】根据线段中点的性质得出,进而根据题意得出,得出,根据,即可求解.
【详解】解:∵点是线段的中点,(已知)
∴.
∵,(已知)
∴.
∵在线段上,,(已知)
∴.
∴.
∴.
故答案为:,,,,.
【点睛】本题考查了线段中点的性质,线段和差的计算,数形结合是解题的关键.
24.,图见解析
【分析】实践与操作:在射线上分别顺次截取线段,即可.
推理与计算:先求出长,再根据线段的中点求出和长,即可求出答案;
【详解】实践与操作:如图,线段即为所求线段.
推理与计算:
解:由作图可知,,,,
因为点D是的中点,点E是的中点,
所以,,
所以.
【点睛】本题主要考查两点间的距离,掌握中点的定义是解题的关键.
25.(1)《汉语成语大词典》的标价是100元,《中华上下五千年》的标价是50元;
(2)这个包装盒的表面积是;
(3)对礼品盒进行包装,她的钱不够.
【分析】(1)设《汉语成语大词典》的标价是元,则《中华上下五千年》的标价是元,依题意列出一元一次方程,求解即可;
(2)要求长方体的表面积,根据“长方体的表面积长宽长高宽高”,代入数值,进行解答即可;
(3)由包装纸每平方米10元,且包装手工费1元求出对礼品盒进行包装所需的费用,与3元钱进行比较即可.
【详解】(1)解:设《汉语成语大词典》的标价是元,则《中华上下五千年》的标价是元,
根据题意得:,解得:,
(元),
答:《汉语成语大词典》的标价是100元,《中华上下五千年》的标价是50元;
(2)解:,
答:这个包装盒的表面积是;
(3)解:∵包装纸每平方米10元,且包装手工费1元,
∴对礼品盒进行包装所需的费用是:(元),
∵,
∴对礼品盒进行包装,她的钱不够.
【点睛】本题考查了一元一次方程的应用以及代数式求值,掌握长方体的表面积公式是解题的关键.
26.(1),
(2)①5047;②100;③,
(3)①90;②135;③
【分析】(1)根据题目中的规律即可求解;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律得出方程,解方程即可求解;③根据规律即可求解;
(3)①10个城市每两个城市都要互通航班,据此即可求解;②分别计算横向和竖向的线段条数,即可求解;③利用分类的方法可求得2022年足球世界杯共进行多少场比赛.
【详解】(1)解:.
则.
故答案为:,;
(2)解:①.
②∵,
∴,解得或(舍去),
则.
③如果该班有名同学,则共击掌次,共赠送祝福语条.
故答案为:①5047;②100;③,;
(3)解:①如图,“北京——广州”航线上有A、B、C、D、E、F、G、H8个城市,如果每两个城市都要互通航班,10个城市一共需要开通架航班;
②横线上的线段有条,竖线上的线段有条,
则横线和竖线上的线段共有条;
③32支比赛分为8个小组,每个小组4支球队,共有场比赛,
16强分成8组对阵,共有8场比赛,
8强分成4组对阵,共有4场比赛,
4强分成2组对阵,共有2场比赛,
决赛有2场比赛,
故共有场比赛.
故答案为:①90;②135;③64.
【点睛】本题考查了探索规律,线段的计数,线段的计数时应注重分类讨论的方法计数,做到不遗漏,不重复,利用规律解决问题.
27.(1)
(2)8、20
【分析】(1)先根据题意算出,再根据即可解答,掌握线段的和差倍分是解题的关键;
(2)①根据P,Q两点第一次相遇时,P,Q两点所走的路程之和是的长列方程求解即可;②根据P,Q两点第二次相遇时,P 点所走的路程与的差以及Q所走的路程与的差相等列方程即可求解;根据线段的和差列出方程是解答本题的关键.
【详解】(1)解:∵,,.
∴,
∴.
故线段的长为.
(2)解:①P,Q两点第一次相遇时,点P运动的路程为,点Q运动的路程为t,
根据题意可知:P,Q两点第一次相遇时,P,Q两点所走的路程之和是,即,解得: 秒
故P,Q两点第一次相遇时,运动时间t的值是8秒;
②P,Q两点第二次相遇时,点P运动的路程为,点Q运动的路程为t,
由(1)得 ,
根据题意可知:P,Q两点第二次相遇时,P 点所走的路程与的差以及Q所走的路程与的差相等,即:,解得: 秒,
∴,
∴.
故P,Q两点第二次相遇时,与点A的距离是.
28.(1)6
(2)6.75cm
(3)3.75cm或9.75cm
【分析】(1)根据线段的定义找出线段即可;
(2)根据线段的中点和两条线段的和的定义,求出结果;
(3)由于点在直线上的具体位置不确定,故应分点在点的左边和点在点的右边两种情况分别求解.
【详解】(1)图中有6条线段,它们是线段,,,,,.
故答案为:6.
(2)点是线段的中点,,
,
点是线段的中点,
,
(3)当点在点的左边,,
,
当点在点的右边,,
故答案为:3.75cm或9.75cm.
【点睛】本题主要考查了两点间的距离,线段中点的定义和线段和差的定义,熟练掌握各线段之间的和差以及倍数关系是解本题的关键.
29.(1);(2);(3)
【分析】(1)求得,利用角平分线的定义得,据此求解即可;
(2)求得,利用角平分线的定义得,据此求解即可;
(3)求得,利用角平分线的定义得求解即可.
【详解】解:(1)因为,所以,
因为平分,平分,
所以,,
所以
;
故答案为:;
(2)因为,所以,
因为平分,ON平分,
所以,,
所以
;
(3)因为,所以,
因为平分,平分,
所以,,
所以
.
【点睛】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
30.(1)
(2)
(3)的度数为或
【分析】(1)为直角三角板,所以,又因为,所以;
(2)平分,所以,又因为,根据,得到,,即可得到;
(3)分类讨论,当OQ在直线AB上方时并做图;当OQ在直线AB下方时并做图,根据图形信息和条件信息进行列式计算即可.
【详解】(1)∵ 为直角三角板,
∴ ,
∵,,
∴ ;
(2)∵平分,
∴ ,
∵ ,
设,则,
∵ ,
∴,,
∴ ,,
由(1)得,
∴ ,
(3)①如图,当在直线上方时,
∵ ,∴ ,
∵ 平分,∴,
∵ ,∴,
②如图,当在直线下方时,
∵ ,∴ ,
∵ 平分,∴ ,
∵ ,∴ ;
综上所述:的度数为或.
【点睛】本题主要考查了角平分线的定义及角的计算,熟练掌握角平分线的定义及角的计算的方法进行求解是解决本题的关键.
31.(1)
(2)5;10.5
(3)3或4.5秒
【分析】(1)由计算即可得到答案;
(2)由(1)得,,当边落在边上,刚好旋转的度数为的度数,
因此;
先求出旋转的角度,再根据时间=路程÷速度,进行计算即可求解;
(3)分两种情况:边与边相遇前;边与边相遇后,列方程进行计算即可得到
答案.
【详解】(1)解:,,,
,
故答案为:;
(2)解:由(1)得,,
当边落在边上,刚好旋转的度数为的度数,
三角尺绕点逆时针旋转的速度为以每秒,
,
故答案为:5;
当边平分时,画出图如图所示,
边平分,
,
旋转角度为,
,
故答案为:10.5;
(3)解:由(1)可知,两个三角尺旋转前,,边旋转的角度为,边旋转的角度为,
边与边相遇前,可得:,
解得:;
边与边相遇后,可得:,
解得:,
为3或4.5秒时,.
【点睛】本题考查了几何图形中角度的计算、与角平分线有关的角度的计算、旋转的性质、一元一次方程的应用,熟练掌握以上知识点,采用分类讨论的思想解题,是解题的关键.
32.(1)
(2)
【分析】(1)根据折叠的性质得出,,求解即可;
(2)由折叠知,再由角平分线及邻补角得出,结合图形,进行等量代换求解即可.
【详解】(1)解:由折叠知,
同理:
∴
(2)由折叠知,
又∵
∴
∵平分
∴
∵
∴
∴
∴.
【点睛】题目主要考查角平分线及角度的计算,结合图形,找准各角之间的关系是解题关键.
