人教版数学九年级全册 期末知识点 复习课件(共102张PPT)
文档属性
| 名称 | 人教版数学九年级全册 期末知识点 复习课件(共102张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 11:35:14 | ||
图片预览










文档简介
(共102张PPT)
八年级上册数学期末
各单元整合复习
整册复习讲评
二十一章、一元二次方程
一、一元二次方程的基本概念
1.定义:
只含有一个未知数的整式方程,并且都可以化为 ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
要点梳理
3.项数和系数:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
一次项: ax2 一次项系数:a
二次项: bx 二次项系数:b
常数项:c
4.注意事项:
(1)含有一个未知数; (2)未知数的最高次数为2;
(3)二次项系数不为0; (4)整式方程.
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
各种一元二次方程的解法及使用类型
三、一元二次方程在生活中的应用
列方程解应用题的一般步骤:
审
设
列
解
检
答
(1)审题:通过审题弄清已知量与未知量之间的数量关系.
(2)设元:就是设未知数,分直接设与间接设,应根据实际需要恰当选取设元法.
(3)列方程:就是建立已知量与未知量之间的等量关系.列方程这一环节最重要,决定着能否顺利解决实际问题.
(4)解方程:正确求出方程的解并注意检验其合理性.
(5)作答:即写出答语,遵循问什么答什么的原则写清答语.
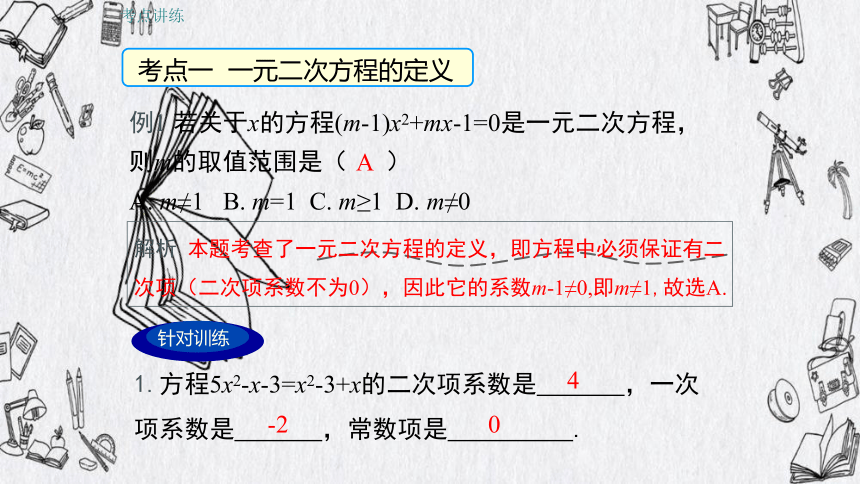
考点一 一元二次方程的定义
例1 若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m≥1 D. m≠0
解析 本题考查了一元二次方程的定义,即方程中必须保证有二次项(二次项系数不为0),因此它的系数m-1≠0,即m≠1,故选A.
A
1.方程5x2-x-3=x2-3+x的二次项系数是 ,一次项系数是 ,常数项是 .
4
-2
0
考点讲练
针对训练
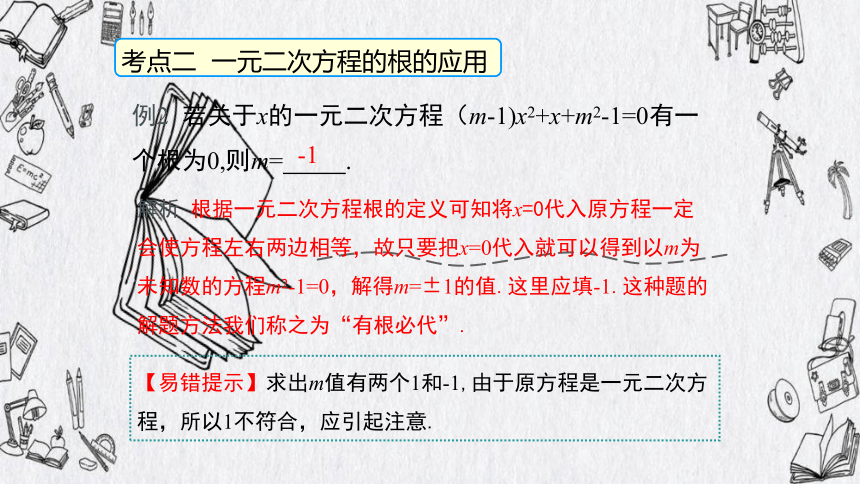
考点二 一元二次方程的根的应用
解析 根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2 若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
【易错提示】求出m值有两个1和-1,由于原方程是一元二次方程,所以1不符合,应引起注意.
-1
【易错提示】(1)配方法的前提是二次项系数是1;(a-b)2与(a+b)2 要准确区分;(2)求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否成三角形的好习惯
解析 (1)配方法的关键是配上一次项系数一半的平方;
(2)先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系定理,得到符合题意的边,进而求得三角形周长.
考点三 一元二次方程的解法
例3 (1)用配方法解方程x2-2x-5=0时,原方程应变为( )
A. (x-1)2=6 B.(x+2)2=9
C. (x+1)2=6 D.(x-2)2=9
(2) (易错题)三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的根,则该三角形的周长为( )
A.13 B. 15 C.18 D.13或18
A
A
考点四 一元二次方程的根的判别式的应用
例4 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数根,则m的取值范围是( )
A. B. m<2 C. m ≥0 D. m<0
A
【易错提示】应用根的判别式之前务必将方程化为一般形式,这样能帮助我们正确确定a,b,c的值.
解析 根据方程根的情况可知,此方程的根的判别式 >0,即42-4×1×(-3m)=16+12m>0,解得 ,故选A.
Δ
考点五 一元二次方程的根与系数的关系
例5 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
【重要变形】
考点六 一元二次方程的应用
例6 某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
市场销售问题
解析 本题为销售中的利润问题,其基本本数量关系用表析分如下:设公司每天的销售价为x元.
单件利润 销售量(件) 每星期利润(元)
正常销售
涨价销售
4
32
x-20
32-2(x-24)
150
其等量关系是:总利润=单件利润×销售量.
解:(1)32-(x-24) ×2=80-2x;
(2)由题意可得(x-20)(80-2x)=150.
解得 x1=25, x2=35.
由题意x≤28, ∴x=25,即售价应当为25元.
【易错提示】销售量在正常销售的基础上进行减少.要注意验根.
128
例7 菜农小王种植的某种蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该种蔬菜滞销.小王为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少?
解:设平均每次下调的百分率是x,根据题意得
5(1-x)2=3.2
解得 x1=1.8 (舍去), x2=0.2=20%.
答:平均每次下调的百分率是20%.
平均变化率问题
例8 为了响应市委政府提出的建设绿色家园的号召,我市某单位准备将院内一个长为30m,宽为20m的长方形空地,建成一个矩形的花园,要求在花园中修两条纵向平行和一条弯折的小道,剩余的地方种植花草,如图所示,要是种植花草的面积为532m2,,那么小道的宽度应为多少米?(所有小道的进出口的宽度相等,且每段小道为平行四边形)
解:设小道进出口的宽为xcm
(30-2x)(20-x)=532
x2-35x+34=0
x1=1 x2=34(舍去)
答:小道进出口的宽度应为1米.
解决有关面积问题时,除了对所学图形面积公式熟悉外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(注意:这里的横坚斜小路的的宽度都相等)
平移转化
方法总结
一元二次方程
一元二次方
程的定义
概念:①整式方程; ②一元; ③二次.
一般形式:ax2+bx+c=0 (a≠0)
一元二次方程的解法
直接开平方法
配方法
公式法
因式分解法
根的判别式及
根与系数的关系
根的判别式: Δ=b2-4ac
根与系数的关系
一元二次方程的应用
营销问题、平均变化率问题
几何问题、数字问题
二十二 章、二次函数
要点梳理
一般地,形如 (a,b,c是常数, __)的函数,叫做二次函数.
y=ax2+bx+c
a ≠0
[注意] (1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
1.二次函数的概念
二次函数 y=a(x-h)2+k y=ax2+bx+c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 2.二次函数的图象与性质:
a>0 开口向上
a < 0 开口向下
x=h
(h , k)
y最小=k
y最大=k
在对称轴左边,x↗ y↘;在对称轴右边, x↗ y↗
在对称轴左边,x↗ y↗;在对称轴右边, x↗ y↘
y最小=
y最大=
3.二次函数图像的平移
y=ax2
左、右平移 左加右减
上、下平移 上加下减
y=-ax2
写成一般形式
沿x轴翻折
4.二次函数表达式的求法
1.一般式法:y=ax2+bx+c (a≠ 0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
5.二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有两个重合的交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图像和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有两个重合的交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
6.二次函数的应用
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图像求一元二次方程的近似解.
2.一般步骤:(1)找出问题中的变量和常量以及它们之间 的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
考点一 求抛物线的顶点、对称轴、最值
考点讲练
例1 抛物线y=x2-2x+3的顶点坐标为________.
【解析】
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二代入公式 , ,
则顶点坐标为(1,2).
(1,2)
方法归纳解决此类题目可以先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);也可以直接利用公式求解.
考点二 二次函数的图像与性质及函数值的大小比较
例2 二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数图像上,且x1A. y1≤y2 B.y1C.y1≥y2 D.y1>y2
【解析】由图像看出,抛物线开口向下,对称轴是x=1,当x<1时,y随x的增大而增大.
∵x1B
考点三 二次函数 y=ax2+bx+c(a≠0)的图像与
系数a,b,c的关系
例3 已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是( )
A.1 B.2 C.3 D.4
D
考点四 抛物线的几何变换
例4 将抛物线y=x2-6x+5向上平移 2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
【解析】因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的解析式为y=(x-3-1)2-4+2,即y= (x-4)2-2.故选B.
考点五 二次函数表达式的确定
例5 已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
待定系数法
解:设所求的二次函数为y=ax2+bx+c, 由题意得:
解得, a=2,b=-3,c=5.
∴ 所求的二次函数为y=2x2-3x+5.
例6 若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6 B.x1=1,x2=7
C.x1=1,x2=﹣7 D.x1=﹣1,x2=7
解析:∵二次函数y=x2+mx的对称轴是x=3,
∴ =3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
考点六 二次函数与一元二次方程
例7 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
考点七 二次函数的应用
解:(1)根据题意,得
解得k=-1,b=120.故所求一次函数的表达式为y=-x+120.
(2)W=(x-60) (-x+120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下, ∴当x<90时,W随x的增大而增大,
而60≤x≤60×(1+45%),即60≤x≤87,
∴当x=87时,W有最大值,此时W=-(87-90)2+900=891.
例8 如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长;
(2)设四边形DEBG的面积为S,求S与x的函数关系式;
(3)当x为何值时,S有最大值?并求出这个最大值.
解:(1)由题意,得EF=AE=DE=BC=x,AB=30.
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF-=∠ABC=90°,
∴∠BGF=∠F=45°,BG=BF=2x-30.
所以S△DEF-S△GBF= DE2- BF2= x2- (2x-30)2=
x2+60x-450.
(3)S= x2+60x-450= (x-20)2+150.
∵a= <0,15<20<30,
∴当x=20时,S有最大值,
最大值为150.
二次函数
二次函数的概念
二次函数与一元二次方程的联系
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数的应用
二十三 章、旋 转
一、旋转的特征
1.旋转过程中,图形上______________________
按 旋转 .
2.任意一对对应点与旋转中心的连线所成的角都是
________,对应点到旋转中心的距离都________.
3.旋转前后对应线段、对应角分别____,图形的大小、形状_________.
每一点都绕旋转中心
同一旋转方向
同样大小的角度
旋转角
相等
相等
不变
要点梳理
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
二、中心对称
2.中心对称的特征
中心对称的特征:在成中心对称的两个图形中,对应点所连线段都经过 ,并且被对称中心________.
3.中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称中心
平分
考点一 旋转的概念及性质的应用
例1 (1)如图a,将三角形AOB绕点O按逆时针方
向旋转60 °后得到三角形COD,若∠AOB=15 °,
则∠AOD的度数是( )
A. 15 ° B. 60 °
C. 45 ° D. 75 °
A
B
O
D
C
图a
C
【解析】关键找出旋转角∠BOD=60 °;
考点讲练
(2) 如图b ,4 ×4的正方形网格中, 三角形MNP绕某
点旋转一定的角度,得到三角形M1N1P1,其旋转中
心是( )
A. 点A B. 点B C. 点C D. 点D
N1
M1
N
M
P1
D
P
A
B
图b
C
B
【解析】作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
1.如图,在4×4的正方形网格中,每个小正方形的边长均为1,将三角形AOB绕点O逆时针旋转90°得到三角形COD,则旋转过程中形成的阴影部分的面积为________.
针对训练
考点二 旋转变换
例2 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
解析:(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
例3 如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
例4 如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它
把纸片分成面积相等的两部分.
l
考点三 中心对称
例5 下列图形中,既是轴对称图形,又是中心对称图形的是( ).
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
方法总结
例6:如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法.
m
考点四 图形变换的简单应用
解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是 .
m
旋转的概念
旋转中心
旋转方向
旋转角度
旋转的三要素
基本
性质
①旋转前后的图形全等
②对应点到旋转中心的距离相等
旋 转
图形的旋转
③对应点与旋转中心所连线段的夹角等于旋转角
旋转
作图
定
找
旋
连
中心对称
中心对称
定义
旋转180 °
性质
对称中心是对称点连线段的中点(即两个对称点与对称中心三点共线
中心对称图形
性质
经过对称中心的直线把原图形面积平分
第二十四章 圆
·
一.与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
4.劣弧:小于半圆周的圆弧.
5.优弧:大于半圆周的圆弧.
要点梳理
6.等弧:在同圆或等圆中,能够互相重合的弧.
7.圆心角:顶点在圆心,角的两边与圆相交.
8.圆周角:顶点在圆上,角的两边与圆相交.
[注意] (1)确定圆的要素:圆心决定位置,半径决定大小.(2)不在同一条直线上的三个点确定一个圆.
·
9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆.
10.三角形的外接圆
外心:三角形的外接圆的圆心叫做这个这个三角形的外心.
[注意] (1)三角形的外心是三角形三条边的垂直平分线的交点.(2)一个三角形的外接圆是唯一的.
11.三角形的内切圆
内心:三角形的内切圆的圆心叫做这个这个三角形的内心.
[注意] (1)三角形的内心是三角形三条角平分线的交点.(2)一个三角形的内切圆是唯一的.
12.正多边形的相关概念
(1)中心:正多变形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
(2)半径:外接圆的半径叫做正多边形的半径.
(3)边心距:中心到正多边形一边的距离叫做正多边形的边心距.
(4)中心角:正多边形每一条边对应所对的外接圆的圆心角都相等,叫做正多边形的中心角.
二、与圆有关的位置关系
1.点与圆的位置关系
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.
设☉O的半径是r,点P到圆心的距离为d,则有
点P在圆内;
d<r
点P在圆上;
d=r
点P在圆外.
d>r
[注意]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反过来,也可以通过这种数量关系判断点与圆的位置关系.
2.直线与圆的位置关系
设r为圆的半径,d为圆心到直线的距离
直线与圆的 位置关系
图形
d与r的关系
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
d>r
d=r
d<r
三、 圆的基本性质
1. 圆的对称性
圆是轴对称图形,它的任意一条_______所在的直线都是它的对称轴.
直径
2. 有关圆心角、弧、弦的性质.
(1)在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
圆心角
相等
弧
相等
弦
相等
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
三、 有关定理及其推论
1.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的 .
[注意] ①条件中的“弦”可以是直径;②结论中的“平分弧”指平分弦所对的劣弧、优弧.
两条弧
2.圆周角定理
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
(3)推论2:90°的圆周角所对的弦是直径.
[注意] “同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
(4)推论3:圆的内接四边形的对角互补.
(2)推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对弧相等.
3.与切线相关的定理
(1)判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
(2)性质定理:圆的切线垂直于经过切点的半径.
(3)切线长定理:经过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
四、 圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S= ____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
(3)圆锥的侧面积为 .
(4)圆锥的全面积为 .
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个 .
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为 .
扇形
l
5.圆内接正多边形的计算
(1)正n边形的中心角为
(2)正n边形的边长a,半径R,边心距r之间的关系
(3)边长a,边心距r的正n边形的面积为
其中l为正n边形的周长.
考点一 圆周角定理
例1 在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
B
考点二 垂径定理
例2 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
8mm
A
B
8
C
D
O
解析 设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
例3 如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.
(1)求证:CD与☉O相切;
A
B
C
D
O
M
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,
∴ CD与☉O相切.
N
考点三 与圆有关的位置关系
A
B
C
D
O
M
(2)解: ∵正方形ABCD的边长为1,AC= .
设☉O的半径为r,则OC= .
又易知△OMC是等腰直角三角形, ∴OC=
因此有 ,解得 .
(2)若正方形ABCD的边长为1,求☉O的半径.
方法归纳
(1)证切线时添加辅助线的解题方法有两种: ①有公共点,连半径,证垂直; ②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;
(2)设未知数,通常利用勾股定理建立方程.
例4 已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∵⊙O分别切PA、PB、DE于点A、B、C,∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∴∠DOE= ∠AOB.
∵∠P+∠AOB=180°,∠P=70°,
∴∠DOE=55°.
(2)∵⊙O分别切PA、PB、DE于A、B、C,
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
(2)若PA=4 cm,求△PDE的周长.
例5 如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?
解:∵四边形OABC为菱形
∴OC=OA=1
∵ ∠AOC=120°,∠1=∠2
∴ ∠FOE=120°
又∵点C在以点O为圆心的圆上
考点四 圆中的计算问题
例6 如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
当图中出现圆的直径时,一般方法是作出直径所对的圆周角,从而利用“直径所对的圆周角等于 ”构造出直角三角形,为进一步利用勾股定理或锐角三角函数提供了条件.
方法总结
考点五 与圆有关的作图
·
a
b
c
d
a
例7 如何解决“破镜重圆”的问题:
O
·
例8 如何作圆内接正五边形怎么作?
·
O
E
72°
B
A
D
C
(1)用量角器作72°的中心角,得圆的五等分点;
(2)依次连接各等分点,得圆的内接正五边形.
圆
圆的性质
与圆有关的位置关系
弧长与扇形面积的计算
圆的对称性
圆是中心对称图形
垂径定理
四边形的内接圆、三角形的外接圆
直线与圆的位置的关系
切线长定理
圆的概念
圆心角、圆周角、弧与弦之间的关系
圆是轴对称图形,任意一条直径所在直线都是它的对称轴
切线
三角形的内切圆
正多边形与圆
作图
第二十五章 概率初步
一、事件的分类及其概念
要点梳理
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随
机事件.
1.概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
二、概率的概念
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
2.
三、随机事件的概率的求法
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件
可能性的大小,但频率具有随机性,概率是自身固有
的性质,不具有随机性.
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)= + +…+
n
1
n
1
n
1
m个
=
n
m
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
四、列表法
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
五、树状图法
考点一 事件的判断和概率的意义
考点讲练
例1 下列事件是随机事件的是( )
A.明天太阳从东方升起
B.任意画一个三角形,其内角和是360°
C.通常温度降到0℃以下,纯净的水结冰
D.射击运动员射击一次,命中靶心
D
1.“闭上眼睛从布袋中随机地摸出1个球,恰是红球的概率是 ”的意思是( )
A.布袋中有2个红球和5个其他颜色的球
B.如果摸球次数很多,那么平均每摸7次,就有2次摸中红球
C.摸7次,就有2次摸中红球
D.摸7次,就有5次摸不中红球
B
针对训练
2.下列事件中是必然事件的是( )
A.从一个装有蓝、白两色球的缸里摸出一个球,摸出的球是白球
B.小丹的自行车轮胎被钉子扎坏
C.小红期末考试数学成绩一定得满分
D.将油滴入水中,油会浮在水面上
D
考点二 用列举法求概率
例2 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A. B. C. D.
C
例3 如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象经过
二、三、四象限的概率.
解:(1)P(k为负数)= .
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为 ;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,
所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
(2)画树状图如右:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)= .
考点三 用频率估计概率
例4 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
例5 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数最有可能是( )
A.24个 B.18个 C.16个 D.6个
C
考点五 用概率作决策
例6 在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)列表如下
6 7 8
2 (6,2) (7,2) (8,2)
4 (6,4) (7,4) (8,4)
6 (6,6) (7,6) (8,6)
卡片
小球
共有9种等可能结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
规则1:P(小红赢)= ;
规则2:P(小红赢)=
∵ , ∴小红选择规则1.
概率初步
随机事件与概率
事件
必然事件
不可能事件
随机事件
概率
定义
刻画随机事件发生可能性大小的数值
计算公式
列举法求概率
直接列举法
列表法
画树状图法
适合于两个试验因素或分两步进行
适合于三个试验因素或分三步进行
用频率估计概率
频率与概率的关系
在大量重复试验中,频率具有
稳定性时才可以用来估计概率
八年级上册数学期末
各单元整合复习
整册复习讲评
二十一章、一元二次方程
一、一元二次方程的基本概念
1.定义:
只含有一个未知数的整式方程,并且都可以化为 ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
要点梳理
3.项数和系数:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
一次项: ax2 一次项系数:a
二次项: bx 二次项系数:b
常数项:c
4.注意事项:
(1)含有一个未知数; (2)未知数的最高次数为2;
(3)二次项系数不为0; (4)整式方程.
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
各种一元二次方程的解法及使用类型
三、一元二次方程在生活中的应用
列方程解应用题的一般步骤:
审
设
列
解
检
答
(1)审题:通过审题弄清已知量与未知量之间的数量关系.
(2)设元:就是设未知数,分直接设与间接设,应根据实际需要恰当选取设元法.
(3)列方程:就是建立已知量与未知量之间的等量关系.列方程这一环节最重要,决定着能否顺利解决实际问题.
(4)解方程:正确求出方程的解并注意检验其合理性.
(5)作答:即写出答语,遵循问什么答什么的原则写清答语.
考点一 一元二次方程的定义
例1 若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m≥1 D. m≠0
解析 本题考查了一元二次方程的定义,即方程中必须保证有二次项(二次项系数不为0),因此它的系数m-1≠0,即m≠1,故选A.
A
1.方程5x2-x-3=x2-3+x的二次项系数是 ,一次项系数是 ,常数项是 .
4
-2
0
考点讲练
针对训练
考点二 一元二次方程的根的应用
解析 根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2 若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
【易错提示】求出m值有两个1和-1,由于原方程是一元二次方程,所以1不符合,应引起注意.
-1
【易错提示】(1)配方法的前提是二次项系数是1;(a-b)2与(a+b)2 要准确区分;(2)求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否成三角形的好习惯
解析 (1)配方法的关键是配上一次项系数一半的平方;
(2)先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系定理,得到符合题意的边,进而求得三角形周长.
考点三 一元二次方程的解法
例3 (1)用配方法解方程x2-2x-5=0时,原方程应变为( )
A. (x-1)2=6 B.(x+2)2=9
C. (x+1)2=6 D.(x-2)2=9
(2) (易错题)三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的根,则该三角形的周长为( )
A.13 B. 15 C.18 D.13或18
A
A
考点四 一元二次方程的根的判别式的应用
例4 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数根,则m的取值范围是( )
A. B. m<2 C. m ≥0 D. m<0
A
【易错提示】应用根的判别式之前务必将方程化为一般形式,这样能帮助我们正确确定a,b,c的值.
解析 根据方程根的情况可知,此方程的根的判别式 >0,即42-4×1×(-3m)=16+12m>0,解得 ,故选A.
Δ
考点五 一元二次方程的根与系数的关系
例5 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
【重要变形】
考点六 一元二次方程的应用
例6 某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
市场销售问题
解析 本题为销售中的利润问题,其基本本数量关系用表析分如下:设公司每天的销售价为x元.
单件利润 销售量(件) 每星期利润(元)
正常销售
涨价销售
4
32
x-20
32-2(x-24)
150
其等量关系是:总利润=单件利润×销售量.
解:(1)32-(x-24) ×2=80-2x;
(2)由题意可得(x-20)(80-2x)=150.
解得 x1=25, x2=35.
由题意x≤28, ∴x=25,即售价应当为25元.
【易错提示】销售量在正常销售的基础上进行减少.要注意验根.
128
例7 菜农小王种植的某种蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该种蔬菜滞销.小王为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少?
解:设平均每次下调的百分率是x,根据题意得
5(1-x)2=3.2
解得 x1=1.8 (舍去), x2=0.2=20%.
答:平均每次下调的百分率是20%.
平均变化率问题
例8 为了响应市委政府提出的建设绿色家园的号召,我市某单位准备将院内一个长为30m,宽为20m的长方形空地,建成一个矩形的花园,要求在花园中修两条纵向平行和一条弯折的小道,剩余的地方种植花草,如图所示,要是种植花草的面积为532m2,,那么小道的宽度应为多少米?(所有小道的进出口的宽度相等,且每段小道为平行四边形)
解:设小道进出口的宽为xcm
(30-2x)(20-x)=532
x2-35x+34=0
x1=1 x2=34(舍去)
答:小道进出口的宽度应为1米.
解决有关面积问题时,除了对所学图形面积公式熟悉外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(注意:这里的横坚斜小路的的宽度都相等)
平移转化
方法总结
一元二次方程
一元二次方
程的定义
概念:①整式方程; ②一元; ③二次.
一般形式:ax2+bx+c=0 (a≠0)
一元二次方程的解法
直接开平方法
配方法
公式法
因式分解法
根的判别式及
根与系数的关系
根的判别式: Δ=b2-4ac
根与系数的关系
一元二次方程的应用
营销问题、平均变化率问题
几何问题、数字问题
二十二 章、二次函数
要点梳理
一般地,形如 (a,b,c是常数, __)的函数,叫做二次函数.
y=ax2+bx+c
a ≠0
[注意] (1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
1.二次函数的概念
二次函数 y=a(x-h)2+k y=ax2+bx+c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 2.二次函数的图象与性质:
a>0 开口向上
a < 0 开口向下
x=h
(h , k)
y最小=k
y最大=k
在对称轴左边,x↗ y↘;在对称轴右边, x↗ y↗
在对称轴左边,x↗ y↗;在对称轴右边, x↗ y↘
y最小=
y最大=
3.二次函数图像的平移
y=ax2
左、右平移 左加右减
上、下平移 上加下减
y=-ax2
写成一般形式
沿x轴翻折
4.二次函数表达式的求法
1.一般式法:y=ax2+bx+c (a≠ 0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
5.二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有两个重合的交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图像和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有两个重合的交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
6.二次函数的应用
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图像求一元二次方程的近似解.
2.一般步骤:(1)找出问题中的变量和常量以及它们之间 的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
考点一 求抛物线的顶点、对称轴、最值
考点讲练
例1 抛物线y=x2-2x+3的顶点坐标为________.
【解析】
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二代入公式 , ,
则顶点坐标为(1,2).
(1,2)
方法归纳解决此类题目可以先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);也可以直接利用公式求解.
考点二 二次函数的图像与性质及函数值的大小比较
例2 二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数图像上,且x1
【解析】由图像看出,抛物线开口向下,对称轴是x=1,当x<1时,y随x的增大而增大.
∵x1
考点三 二次函数 y=ax2+bx+c(a≠0)的图像与
系数a,b,c的关系
例3 已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是( )
A.1 B.2 C.3 D.4
D
考点四 抛物线的几何变换
例4 将抛物线y=x2-6x+5向上平移 2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
【解析】因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的解析式为y=(x-3-1)2-4+2,即y= (x-4)2-2.故选B.
考点五 二次函数表达式的确定
例5 已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
待定系数法
解:设所求的二次函数为y=ax2+bx+c, 由题意得:
解得, a=2,b=-3,c=5.
∴ 所求的二次函数为y=2x2-3x+5.
例6 若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6 B.x1=1,x2=7
C.x1=1,x2=﹣7 D.x1=﹣1,x2=7
解析:∵二次函数y=x2+mx的对称轴是x=3,
∴ =3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
考点六 二次函数与一元二次方程
例7 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
考点七 二次函数的应用
解:(1)根据题意,得
解得k=-1,b=120.故所求一次函数的表达式为y=-x+120.
(2)W=(x-60) (-x+120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下, ∴当x<90时,W随x的增大而增大,
而60≤x≤60×(1+45%),即60≤x≤87,
∴当x=87时,W有最大值,此时W=-(87-90)2+900=891.
例8 如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长;
(2)设四边形DEBG的面积为S,求S与x的函数关系式;
(3)当x为何值时,S有最大值?并求出这个最大值.
解:(1)由题意,得EF=AE=DE=BC=x,AB=30.
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF-=∠ABC=90°,
∴∠BGF=∠F=45°,BG=BF=2x-30.
所以S△DEF-S△GBF= DE2- BF2= x2- (2x-30)2=
x2+60x-450.
(3)S= x2+60x-450= (x-20)2+150.
∵a= <0,15<20<30,
∴当x=20时,S有最大值,
最大值为150.
二次函数
二次函数的概念
二次函数与一元二次方程的联系
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数的应用
二十三 章、旋 转
一、旋转的特征
1.旋转过程中,图形上______________________
按 旋转 .
2.任意一对对应点与旋转中心的连线所成的角都是
________,对应点到旋转中心的距离都________.
3.旋转前后对应线段、对应角分别____,图形的大小、形状_________.
每一点都绕旋转中心
同一旋转方向
同样大小的角度
旋转角
相等
相等
不变
要点梳理
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
二、中心对称
2.中心对称的特征
中心对称的特征:在成中心对称的两个图形中,对应点所连线段都经过 ,并且被对称中心________.
3.中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称中心
平分
考点一 旋转的概念及性质的应用
例1 (1)如图a,将三角形AOB绕点O按逆时针方
向旋转60 °后得到三角形COD,若∠AOB=15 °,
则∠AOD的度数是( )
A. 15 ° B. 60 °
C. 45 ° D. 75 °
A
B
O
D
C
图a
C
【解析】关键找出旋转角∠BOD=60 °;
考点讲练
(2) 如图b ,4 ×4的正方形网格中, 三角形MNP绕某
点旋转一定的角度,得到三角形M1N1P1,其旋转中
心是( )
A. 点A B. 点B C. 点C D. 点D
N1
M1
N
M
P1
D
P
A
B
图b
C
B
【解析】作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
1.如图,在4×4的正方形网格中,每个小正方形的边长均为1,将三角形AOB绕点O逆时针旋转90°得到三角形COD,则旋转过程中形成的阴影部分的面积为________.
针对训练
考点二 旋转变换
例2 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
解析:(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
例3 如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
例4 如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它
把纸片分成面积相等的两部分.
l
考点三 中心对称
例5 下列图形中,既是轴对称图形,又是中心对称图形的是( ).
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
方法总结
例6:如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法.
m
考点四 图形变换的简单应用
解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是 .
m
旋转的概念
旋转中心
旋转方向
旋转角度
旋转的三要素
基本
性质
①旋转前后的图形全等
②对应点到旋转中心的距离相等
旋 转
图形的旋转
③对应点与旋转中心所连线段的夹角等于旋转角
旋转
作图
定
找
旋
连
中心对称
中心对称
定义
旋转180 °
性质
对称中心是对称点连线段的中点(即两个对称点与对称中心三点共线
中心对称图形
性质
经过对称中心的直线把原图形面积平分
第二十四章 圆
·
一.与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
4.劣弧:小于半圆周的圆弧.
5.优弧:大于半圆周的圆弧.
要点梳理
6.等弧:在同圆或等圆中,能够互相重合的弧.
7.圆心角:顶点在圆心,角的两边与圆相交.
8.圆周角:顶点在圆上,角的两边与圆相交.
[注意] (1)确定圆的要素:圆心决定位置,半径决定大小.(2)不在同一条直线上的三个点确定一个圆.
·
9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆.
10.三角形的外接圆
外心:三角形的外接圆的圆心叫做这个这个三角形的外心.
[注意] (1)三角形的外心是三角形三条边的垂直平分线的交点.(2)一个三角形的外接圆是唯一的.
11.三角形的内切圆
内心:三角形的内切圆的圆心叫做这个这个三角形的内心.
[注意] (1)三角形的内心是三角形三条角平分线的交点.(2)一个三角形的内切圆是唯一的.
12.正多边形的相关概念
(1)中心:正多变形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
(2)半径:外接圆的半径叫做正多边形的半径.
(3)边心距:中心到正多边形一边的距离叫做正多边形的边心距.
(4)中心角:正多边形每一条边对应所对的外接圆的圆心角都相等,叫做正多边形的中心角.
二、与圆有关的位置关系
1.点与圆的位置关系
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.
设☉O的半径是r,点P到圆心的距离为d,则有
点P在圆内;
d<r
点P在圆上;
d=r
点P在圆外.
d>r
[注意]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反过来,也可以通过这种数量关系判断点与圆的位置关系.
2.直线与圆的位置关系
设r为圆的半径,d为圆心到直线的距离
直线与圆的 位置关系
图形
d与r的关系
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
d>r
d=r
d<r
三、 圆的基本性质
1. 圆的对称性
圆是轴对称图形,它的任意一条_______所在的直线都是它的对称轴.
直径
2. 有关圆心角、弧、弦的性质.
(1)在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
圆心角
相等
弧
相等
弦
相等
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
三、 有关定理及其推论
1.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的 .
[注意] ①条件中的“弦”可以是直径;②结论中的“平分弧”指平分弦所对的劣弧、优弧.
两条弧
2.圆周角定理
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
(3)推论2:90°的圆周角所对的弦是直径.
[注意] “同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
(4)推论3:圆的内接四边形的对角互补.
(2)推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对弧相等.
3.与切线相关的定理
(1)判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
(2)性质定理:圆的切线垂直于经过切点的半径.
(3)切线长定理:经过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
四、 圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S= ____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
(3)圆锥的侧面积为 .
(4)圆锥的全面积为 .
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个 .
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为 .
扇形
l
5.圆内接正多边形的计算
(1)正n边形的中心角为
(2)正n边形的边长a,半径R,边心距r之间的关系
(3)边长a,边心距r的正n边形的面积为
其中l为正n边形的周长.
考点一 圆周角定理
例1 在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
B
考点二 垂径定理
例2 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
8mm
A
B
8
C
D
O
解析 设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
例3 如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.
(1)求证:CD与☉O相切;
A
B
C
D
O
M
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,
∴ CD与☉O相切.
N
考点三 与圆有关的位置关系
A
B
C
D
O
M
(2)解: ∵正方形ABCD的边长为1,AC= .
设☉O的半径为r,则OC= .
又易知△OMC是等腰直角三角形, ∴OC=
因此有 ,解得 .
(2)若正方形ABCD的边长为1,求☉O的半径.
方法归纳
(1)证切线时添加辅助线的解题方法有两种: ①有公共点,连半径,证垂直; ②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;
(2)设未知数,通常利用勾股定理建立方程.
例4 已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∵⊙O分别切PA、PB、DE于点A、B、C,∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∴∠DOE= ∠AOB.
∵∠P+∠AOB=180°,∠P=70°,
∴∠DOE=55°.
(2)∵⊙O分别切PA、PB、DE于A、B、C,
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
(2)若PA=4 cm,求△PDE的周长.
例5 如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?
解:∵四边形OABC为菱形
∴OC=OA=1
∵ ∠AOC=120°,∠1=∠2
∴ ∠FOE=120°
又∵点C在以点O为圆心的圆上
考点四 圆中的计算问题
例6 如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
当图中出现圆的直径时,一般方法是作出直径所对的圆周角,从而利用“直径所对的圆周角等于 ”构造出直角三角形,为进一步利用勾股定理或锐角三角函数提供了条件.
方法总结
考点五 与圆有关的作图
·
a
b
c
d
a
例7 如何解决“破镜重圆”的问题:
O
·
例8 如何作圆内接正五边形怎么作?
·
O
E
72°
B
A
D
C
(1)用量角器作72°的中心角,得圆的五等分点;
(2)依次连接各等分点,得圆的内接正五边形.
圆
圆的性质
与圆有关的位置关系
弧长与扇形面积的计算
圆的对称性
圆是中心对称图形
垂径定理
四边形的内接圆、三角形的外接圆
直线与圆的位置的关系
切线长定理
圆的概念
圆心角、圆周角、弧与弦之间的关系
圆是轴对称图形,任意一条直径所在直线都是它的对称轴
切线
三角形的内切圆
正多边形与圆
作图
第二十五章 概率初步
一、事件的分类及其概念
要点梳理
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随
机事件.
1.概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
二、概率的概念
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
2.
三、随机事件的概率的求法
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件
可能性的大小,但频率具有随机性,概率是自身固有
的性质,不具有随机性.
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)= + +…+
n
1
n
1
n
1
m个
=
n
m
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
四、列表法
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
五、树状图法
考点一 事件的判断和概率的意义
考点讲练
例1 下列事件是随机事件的是( )
A.明天太阳从东方升起
B.任意画一个三角形,其内角和是360°
C.通常温度降到0℃以下,纯净的水结冰
D.射击运动员射击一次,命中靶心
D
1.“闭上眼睛从布袋中随机地摸出1个球,恰是红球的概率是 ”的意思是( )
A.布袋中有2个红球和5个其他颜色的球
B.如果摸球次数很多,那么平均每摸7次,就有2次摸中红球
C.摸7次,就有2次摸中红球
D.摸7次,就有5次摸不中红球
B
针对训练
2.下列事件中是必然事件的是( )
A.从一个装有蓝、白两色球的缸里摸出一个球,摸出的球是白球
B.小丹的自行车轮胎被钉子扎坏
C.小红期末考试数学成绩一定得满分
D.将油滴入水中,油会浮在水面上
D
考点二 用列举法求概率
例2 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A. B. C. D.
C
例3 如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象经过
二、三、四象限的概率.
解:(1)P(k为负数)= .
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为 ;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,
所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
(2)画树状图如右:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)= .
考点三 用频率估计概率
例4 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
例5 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数最有可能是( )
A.24个 B.18个 C.16个 D.6个
C
考点五 用概率作决策
例6 在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)列表如下
6 7 8
2 (6,2) (7,2) (8,2)
4 (6,4) (7,4) (8,4)
6 (6,6) (7,6) (8,6)
卡片
小球
共有9种等可能结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
规则1:P(小红赢)= ;
规则2:P(小红赢)=
∵ , ∴小红选择规则1.
概率初步
随机事件与概率
事件
必然事件
不可能事件
随机事件
概率
定义
刻画随机事件发生可能性大小的数值
计算公式
列举法求概率
直接列举法
列表法
画树状图法
适合于两个试验因素或分两步进行
适合于三个试验因素或分三步进行
用频率估计概率
频率与概率的关系
在大量重复试验中,频率具有
稳定性时才可以用来估计概率
同课章节目录
