第11章 三角形 单元复习题 2023-2024学年上学期人教版数学八年级上册(含解析)
文档属性
| 名称 | 第11章 三角形 单元复习题 2023-2024学年上学期人教版数学八年级上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 14:31:35 | ||
图片预览



文档简介
第11章 三角形
一、单选题
1.(2023上·山西阳泉·八年级统考期末)下列图形中,具有稳定性的是( )
A.六边形 B.五边形 C.正方形 D.三角形
2.(2023上·山西运城·八年级统考期末)在探究证明“三角形的内角和等于”时,飞翔班的同学作了如下四种辅助线,其中不能证明“三角形的内角和等于”的是( )
A.延长至D过C作 B.过A作
C.过D作 D.过P作,,
3.(2023上·山西运城·八年级统考期末)把一副三角板放在水平桌面上,摆放成如图所示形状,若,则的度数为( )
A. B. C. D.
4.(2022上·山西朔州·八年级校联考期末)已知等腰三角形一腰上的高与另一腰的夹角为,那么这个等腰三角形的顶角等于( )
A.或 B. C. D.或
5.(2023上·山西晋中·八年级统考期末)如图,的角平分线相交于点O,,则( )
A. B. C. D.
6.(2023上·山西运城·八年级统考期末)下列命题,属于真命题的是( )
A.三角形的外角等于两个内角的和 B.内错角相等,两直线平行
C.一个定理的逆命题就是这个定理的逆定理 D.三角形的一个外角大于任何一个内角
7.(2023上·山西太原·八年级校考期末)如图,已知点是内的一点,连接并延长交于点,连接,给出下列结论:①;②;③,其中正确的为( )
A.只有① B.只有② C.只有①② D.①②③
8.(2023上·山西太原·八年级校考期末)如图,,,则的度数为( )
A. B. C. D.
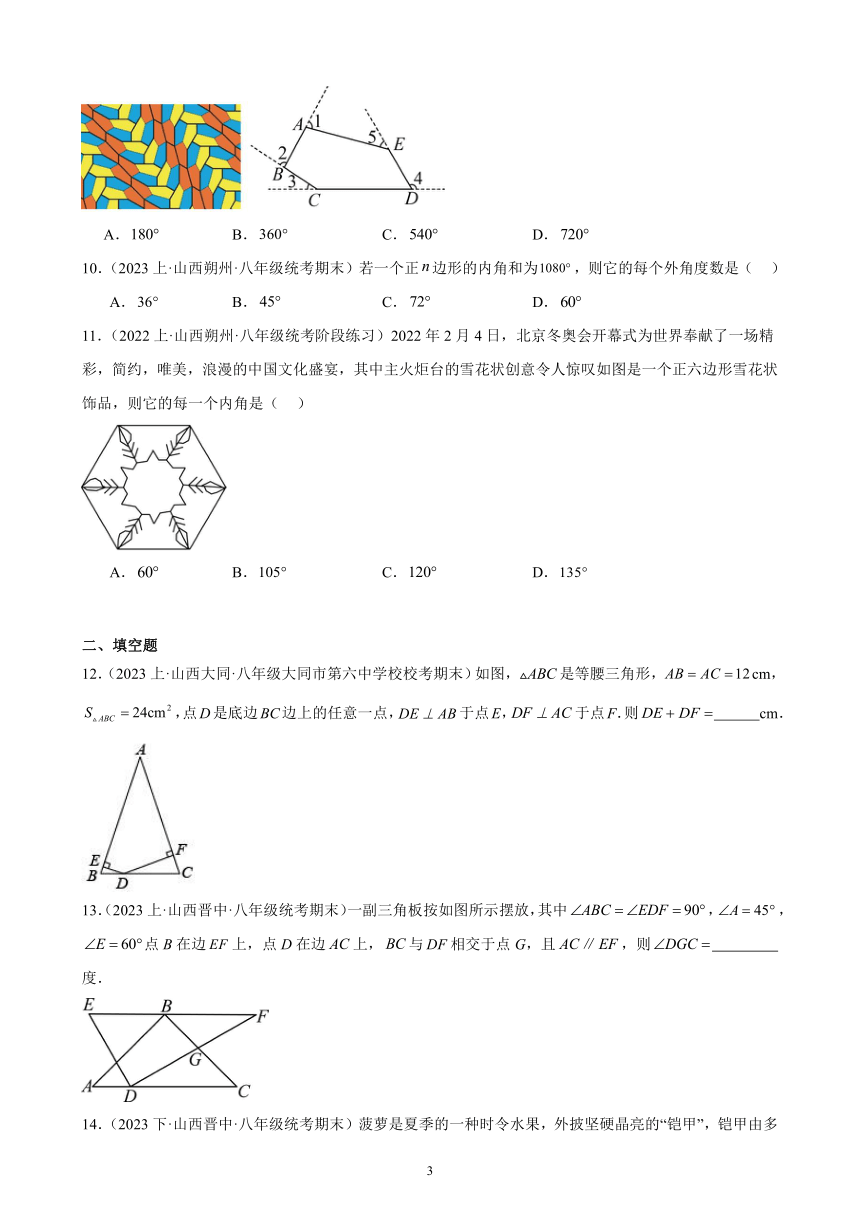
9.(2023下·山西太原·八年级统考期末)完美五边形是指可以无重叠、无间隙铺满整个平面的凸五边形.如图的五边形是迄今为止人类发现的第15种完美五边形,其中的度数和为( )
A. B. C. D.
10.(2023上·山西朔州·八年级统考期末)若一个正边形的内角和为,则它的每个外角度数是( )
A. B. C. D.
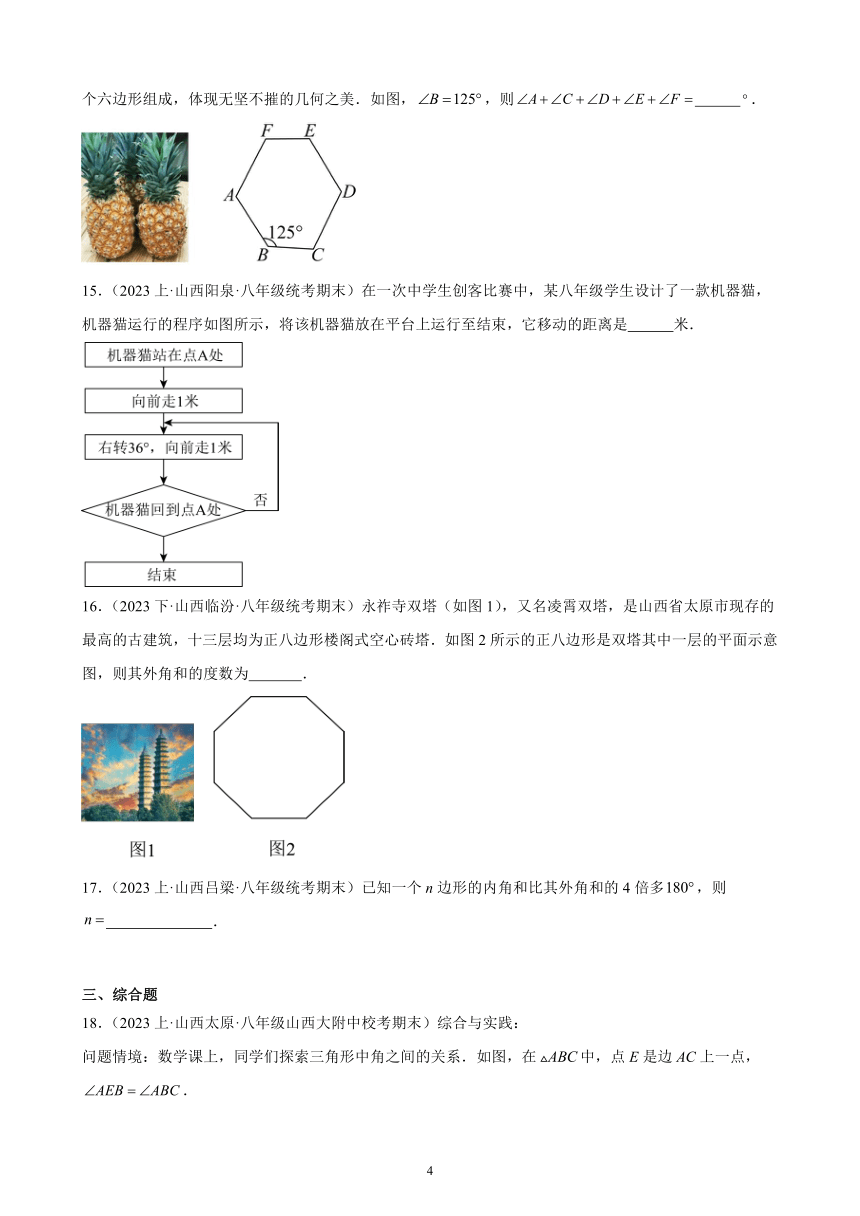
11.(2022上·山西朔州·八年级统考阶段练习)2022年2月4日,北京冬奥会开幕式为世界奉献了一场精彩,简约,唯美,浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A. B. C. D.
二、填空题
12.(2023上·山西大同·八年级大同市第六中学校校考期末)如图,是等腰三角形,cm,,点D是底边BC边上的任意一点,于点E,于点F.则 cm.
13.(2023上·山西晋中·八年级统考期末)一副三角板按如图所示摆放,其中,,点B在边上,点D在边上,与相交于点G,且,则 度.
14.(2023下·山西晋中·八年级统考期末)菠萝是夏季的一种时令水果,外披坚硬晶亮的“铠甲”,铠甲由多个六边形组成,体现无坚不摧的几何之美.如图,,则 .
15.(2023上·山西阳泉·八年级统考期末)在一次中学生创客比赛中,某八年级学生设计了一款机器猫,机器猫运行的程序如图所示,将该机器猫放在平台上运行至结束,它移动的距离是 米.
16.(2023下·山西临汾·八年级统考期末)永祚寺双塔(如图1),又名凌霄双塔,是山西省太原市现存的最高的古建筑,十三层均为正八边形楼阁式空心砖塔.如图2所示的正八边形是双塔其中一层的平面示意图,则其外角和的度数为 .
17.(2023上·山西吕梁·八年级统考期末)已知一个n边形的内角和比其外角和的4倍多,则 .
三、综合题
18.(2023上·山西太原·八年级山西大附中校考期末)综合与实践:
问题情境:数学课上,同学们探索三角形中角之间的关系.如图,在中,点E是边AC上一点,.
特例分析:
(1)如图1,作的平分线交CB、BE于D、F两点.若,,求和.
类比猜想:
(2)奋斗小组在(1)的基础上,改变的大小,经过探究,他们发现与之间存在特定的等量关系,请直接写出这一等量关系.
拓展探究:
(3)如图2,作的外角的平分线,交CB的延长线于点D,延长BE、DA交于点F,请在图2中画出符合题意的图形,并探究(2)中的结论是否成立?若成立,请说明理由;若不成立,请写出结论并说明理由.
19.(2023上·山西太原·八年级校考期末)已知:如图,是内一点,连接,.
(1)猜想:与、、存在怎样的等量关系?证明你的猜想.
(2)若,、分别是、的三等分线,直接利用(1)中结论,可得的度数为 .
20.(2023上·山西晋中·八年级统考期末)请阅读下列材料,并完成相应任务.
在数学探究课上,老师出了这样一个题:如图1,锐角内部有一点D,在其两边和上各取任意一点E,F,连接.
求证:.
小丽的证法 小红的证法
证明: 如图2,连接并延长至点M, , ( 依据 ), 又∵, , ∴. 证明: ∵, (量角器测量所得), ∴, (计算所得). ∴(等量代换).
任务:
(1)小丽证明过程中的“依据”是指数学定理:________________________;
(2)下列说法正确的是____________.
A.小丽的证法用严谨的推理证明了该定理
B.小丽的证法还需要改变的大小,再进行证明,该定理的证明才完整
C.小红的证法用特殊到一般的方法证明了该定理
D.小红的证法只要将点D在的内部任意移动100次,重新测量进行验证,就能证明该定理
(3)如图,若点D在锐角外部,与相交于点G,其余条件不变,原题中结论还成立吗?若成立,请说明理由;若不成立,请探索之间的关系.
21.(2023上·山西太原·八年级校考期末)问题情境:如图1,将含 角的三角板 和含角的三角板 叠放在一起,使直角顶点重合,点 D 落在直线 上,点 E 落在直线 上. 绕点 A 旋转, 边 与 、 分别相交与点 F、点N,边 与 相交于点 M.
(1)如图 2,当 时:
①求的度数.
②判断 与的数量关系,并说明理由.
(2)如图 3,当 平分 时:
①求的度数;
②判断 与 的位置关系,并说明理由.
22.(2023上·山西太原·八年级校考期末)如图,若,垂直为点 D,,,试判断直线与 的位置关系,并说明理由.
参考答案:
1.D
【分析】直接根据三角形的稳定性解答即可.
【详解】解:A、B、C选项中都有四边形,只有D选项中只有三角形,
根据四边形的不稳定性和三角形的稳定性可知:D选项的图形具有稳定性.
故选:D.
【点睛】本题主要考查了三角形的稳定性,掌握组成的所有的图形都是三角形,则具有稳定性是解答本题的关键.
2.C
【分析】根据平行线性质和三角形内角和定理即可求解.
【详解】A、,,,由 ,得 ,故A不符合题意;
B、,,,由 ,得 ,故B不符合题意;
C、,,,无法证得三角形的内角和等于,故C符合题意;
D、如图,,,,,,,,故D不符合题意.
故选:C.
【点睛】本题考查了三角形内角和定理和平行线的性质的知识点,熟悉以上知识点是解题关键.
3.A
【分析】根据三角板得到,,再根据平行线的性质得到,最后利用三角形内角和定理计算即可.
【详解】解:如图,和交于点G,
由三角板可知:,,
∵,
∴,
∴,
故选A.
【点睛】本题考查平行线的性质,三角板的性质,三角形内角和,解题关键是结合图形利用平行线的性质进行角的转化和计算.
4.A
【分析】分别从是锐角三角形与钝角三角形去分析求解即可求得答案.
【详解】解:如图(1),当是锐角三角形时,
,,
,
,
;
如图(2),当是钝角三角形时,
,,
,
,
,;
综上所述,它的顶角度数为:或,
故选:A.
【点睛】此题考查了等腰三角形的性质,三角形内角和定理,采用分类讨论的思想是解此题的关键.
5.C
【分析】根据三角形内角和定理可得,从而得到,再由三角形外角的性质,即可求解.
【详解】解:∵,
∴,
∵的角平分线相交于点O,
∴,
∴.
故选C.
【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,熟练掌握三角形内角和定理,三角形外角的性质是解题的关键.
6.B
【分析】根据三角形外角的性质,平行线的判定,定理与逆定理,逐一进行判断即可.
【详解】解A.三角形的外角等于与它不相邻的两个内角的和,原说法错误,不符合题意;
B.内错角相等,两直线平行,是真命题,符合题意;
C.一个定理的逆命题是真命题,逆命题就是这个定理的逆定理,原说法错误,不符合题意;
D.三角形的一个外角大于任何一个与它不相邻的内角,原说法错误,不符合题意;
故选B.
【点睛】本题考查命题的真假.熟练掌握三角形外角的性质,平行线的判定,定理与逆定理,是解题的关键.
7.D
【分析】由三角形外角的性质可得、、和之间大小关系,即可得到答案.
【详解】解:是的外角,
,,
故①正确;
是的外角,
,
故②③正确;
综上,①②③正确;
故选:D.
【点睛】本题考查了三角形外角的性质,熟练掌握三角形的外角大于不相邻的每一个内角是解题的关键.
8.B
【分析】根据三角形的外角定理即可求解.
【详解】解:∵,,
∴,
故选:B.
【点睛】本题主要考查了三角形的外角定理,解题的关键是掌握三角形的一个外角等于与它不相邻的两个内角之和.
9.B
【分析】直接利用多边形的外角和为即可得出答案.
【详解】解:∵多边形的外角和为,
∴.
故选:B.
【点睛】本题考查了多边形的外角和,熟知多边形的外角和是是解题关键.
10.B
【分析】根据多边形内角和公式列出方程,求出的值,即可求出多边形的边数,再根据多边形的外角和是,利用除以边数可得外角度数.
【详解】解:根据题意,可得,
解得,
所以,外角的度数为.
故选:B.
【点睛】此题主要考查了多边形的内角与外角,解题关键是根据多边形的内角和公式和多边形的外角和为进行解答.
11.C
【分析】根据多边形的内角和公式:多边形的内角和=和正多边形的性质即可求解.
【详解】解:∵正六边形的内角和为:,
又∵正六边形的6个内角都相等,
∴它的每一个内角=.
故选C.
【点睛】本题考查多边形的内角和公式和正多边形的性质.掌握多边形的内角和=与正多边形的每一个内角都相等是解题关键.
12.4
【分析】根据图形可知三角形的面积等于三角形的面积加上三角形的面积,根据面积公式变形计算即可.
【详解】解:∵,
又∵,
,
∴,
∵,
,
,
故答案为:4.
【点睛】本题考查三角形的面积公式,三角形的高,能够熟练掌握割补法求面积是解决本题的关键.
13.105
【分析】根据平行线的性质及三角形内角和定理,即可求解.
【详解】解:,,,
,
,
,
,
故答案为:105.
【点睛】本题主要考查了平行线的性质,三角形内角和定理,解题时注意:两直线平行,内错角相等.
14.
【分析】先求出六边形的内角和,问题即可得解.
【详解】六边形的内角和为:,
即:,
故答案为:.
【点睛】本题主要考查了多边形内角和的计算公式,n边形内角和为:,掌握多边形内角和的计算公式,是解答本题的关键.
15.10
【分析】根据多边形的外角和等于360度除以每次转的角度,得到转的次数,即可计算.
【详解】解:经分析,机器猫回到点,总共转了360度.
机器猫转了(次).
机器猫移动的距离是(米).
故答案为:10.
【点睛】本题主要考查多边形的外角,熟练掌握任意多边形的外角和是360度是解决本题的关键.
16.
【分析】直接根据多边形的外角和为即可得到答案.
【详解】解:根据题意可得:
外角和的度数为:,
故答案为:.
【点睛】本题考查了多边形的外角和,熟练掌握多边形的外角和为是解题的关键.
17.11
【分析】根据多边形内角和公式及外角和,即可列出方程,解方程即可求解.
【详解】解:根据题意得:,
解得,
故答案为:.
【点睛】本题考查了多边形内角和公式及外角和,熟练掌握和运用多边形内角和公式及外角和是解决本题的关键.
18.(1),
(2)
(3)成立,理由见解析
【分析】(1)利用三角形内角和定理先求得,利用角平分线的定义求得,再利用三角形的外角性质即可求解;
(2)同(1)的方法即可求解;
(3)根据角平分线的定义推出,再根据三角形的外角性质即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴,
∵是的平分线,
∴,
∴,
∴;
(2)解:∵是的平分线,
∴,
∵,,
又∵,
∴;
(3)解:成立.
理由如下:画出符合题意的图形,如图,
∵是的角平分线,
∴,
∵是的外角,
∴,
∵是的外角,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】本题考查了三角形的外角性质,角平分线的定义,熟记各图形的性质并准确识图是解题的关键.
19.(1),证明见解析
(2)
【分析】(1)根据三角形内角和定理得到,,再结合,即可得到结论;
(2)先根据三角形内角和定理和角三等分线的定义得到,,,再代入(1)中结论求解即可.
【详解】(1)解:猜想:,
证明:由题意得:,,
∵,,
∴,
∴,
∴,
∴;
(2)解:∵,、分别是、的三等分线,
∴,,,
∴.
故答案为:.
【点睛】本题主要考查了三角形内角和定理,角三等分线的定义,熟知三角形内角和为度是解题的关键.
20.(1)三角形的一个外角等于和它不相邻的两个内角的和
(2)A
(3)不成立,
【分析】(1)连接并延长至点M,根据三角形外角的性质解答即可;
(2)按照定理的证明的一般步骤,从已知出发经过量角器测量,计算,证明,即可得答案;
(3)根据三角形外角的性质得,,整理可得答案
【详解】(1)解:小丽证明过程中的“依据”是指数学定理:三角形的一个外角等于和它不相邻的两个内角的和;
(2)根据定理证明的一般步骤,从已知出发经过量角器测量,计算,证明,故A正确;
(3)不成立,
是的一个外角,
,
为的一个外角,
,
(或).
【点睛】本题考查了三角形的外角,解题的关键是掌握三角形外角的性质:三角形的一个外角等于和它不相邻的两个内角的和.
21.(1)①;②
(2)①;②
【分析】(1)①根据平行线的性质可得,再根据三角形的内角定理即可求解;②根据平行线的性质可得,再求出的度数,最后求出的度数即可;
(2)①根据角平分线的性质,先求出的度数,再求出的度数,最后根据三角形的外角定理即可求解;②根据角平分线的性质,可求出的度数,即可得到,即可得出结论.
【详解】(1)解:①∵,
∴,
∵,
∴;
②由①得,
∴,
∴,
∴.
(2)①∵ 平分,
∴,
∴,
∵,
∴;
②由①可得,
∵,
∴,
∴.
【点睛】本题主要考查了平行线的性质和判定,三角形的外角定理,角平分线的定义,解题的关键是掌握三角形的各个角的度数.
22.,理由见解析
【分析】延长交于D,依据,,即可得到,进而得出.
【详解】解:.理由:
如图,延长交于D,
∵,,
∴,
∵,
∴,
∴,
∴.
【点睛】此题主要考查了平行线的性质与判定,关键是掌握两条直线都和第三条直线平行,那么这两条直线平行.
一、单选题
1.(2023上·山西阳泉·八年级统考期末)下列图形中,具有稳定性的是( )
A.六边形 B.五边形 C.正方形 D.三角形
2.(2023上·山西运城·八年级统考期末)在探究证明“三角形的内角和等于”时,飞翔班的同学作了如下四种辅助线,其中不能证明“三角形的内角和等于”的是( )
A.延长至D过C作 B.过A作
C.过D作 D.过P作,,
3.(2023上·山西运城·八年级统考期末)把一副三角板放在水平桌面上,摆放成如图所示形状,若,则的度数为( )
A. B. C. D.
4.(2022上·山西朔州·八年级校联考期末)已知等腰三角形一腰上的高与另一腰的夹角为,那么这个等腰三角形的顶角等于( )
A.或 B. C. D.或
5.(2023上·山西晋中·八年级统考期末)如图,的角平分线相交于点O,,则( )
A. B. C. D.
6.(2023上·山西运城·八年级统考期末)下列命题,属于真命题的是( )
A.三角形的外角等于两个内角的和 B.内错角相等,两直线平行
C.一个定理的逆命题就是这个定理的逆定理 D.三角形的一个外角大于任何一个内角
7.(2023上·山西太原·八年级校考期末)如图,已知点是内的一点,连接并延长交于点,连接,给出下列结论:①;②;③,其中正确的为( )
A.只有① B.只有② C.只有①② D.①②③
8.(2023上·山西太原·八年级校考期末)如图,,,则的度数为( )
A. B. C. D.
9.(2023下·山西太原·八年级统考期末)完美五边形是指可以无重叠、无间隙铺满整个平面的凸五边形.如图的五边形是迄今为止人类发现的第15种完美五边形,其中的度数和为( )
A. B. C. D.
10.(2023上·山西朔州·八年级统考期末)若一个正边形的内角和为,则它的每个外角度数是( )
A. B. C. D.
11.(2022上·山西朔州·八年级统考阶段练习)2022年2月4日,北京冬奥会开幕式为世界奉献了一场精彩,简约,唯美,浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A. B. C. D.
二、填空题
12.(2023上·山西大同·八年级大同市第六中学校校考期末)如图,是等腰三角形,cm,,点D是底边BC边上的任意一点,于点E,于点F.则 cm.
13.(2023上·山西晋中·八年级统考期末)一副三角板按如图所示摆放,其中,,点B在边上,点D在边上,与相交于点G,且,则 度.
14.(2023下·山西晋中·八年级统考期末)菠萝是夏季的一种时令水果,外披坚硬晶亮的“铠甲”,铠甲由多个六边形组成,体现无坚不摧的几何之美.如图,,则 .
15.(2023上·山西阳泉·八年级统考期末)在一次中学生创客比赛中,某八年级学生设计了一款机器猫,机器猫运行的程序如图所示,将该机器猫放在平台上运行至结束,它移动的距离是 米.
16.(2023下·山西临汾·八年级统考期末)永祚寺双塔(如图1),又名凌霄双塔,是山西省太原市现存的最高的古建筑,十三层均为正八边形楼阁式空心砖塔.如图2所示的正八边形是双塔其中一层的平面示意图,则其外角和的度数为 .
17.(2023上·山西吕梁·八年级统考期末)已知一个n边形的内角和比其外角和的4倍多,则 .
三、综合题
18.(2023上·山西太原·八年级山西大附中校考期末)综合与实践:
问题情境:数学课上,同学们探索三角形中角之间的关系.如图,在中,点E是边AC上一点,.
特例分析:
(1)如图1,作的平分线交CB、BE于D、F两点.若,,求和.
类比猜想:
(2)奋斗小组在(1)的基础上,改变的大小,经过探究,他们发现与之间存在特定的等量关系,请直接写出这一等量关系.
拓展探究:
(3)如图2,作的外角的平分线,交CB的延长线于点D,延长BE、DA交于点F,请在图2中画出符合题意的图形,并探究(2)中的结论是否成立?若成立,请说明理由;若不成立,请写出结论并说明理由.
19.(2023上·山西太原·八年级校考期末)已知:如图,是内一点,连接,.
(1)猜想:与、、存在怎样的等量关系?证明你的猜想.
(2)若,、分别是、的三等分线,直接利用(1)中结论,可得的度数为 .
20.(2023上·山西晋中·八年级统考期末)请阅读下列材料,并完成相应任务.
在数学探究课上,老师出了这样一个题:如图1,锐角内部有一点D,在其两边和上各取任意一点E,F,连接.
求证:.
小丽的证法 小红的证法
证明: 如图2,连接并延长至点M, , ( 依据 ), 又∵, , ∴. 证明: ∵, (量角器测量所得), ∴, (计算所得). ∴(等量代换).
任务:
(1)小丽证明过程中的“依据”是指数学定理:________________________;
(2)下列说法正确的是____________.
A.小丽的证法用严谨的推理证明了该定理
B.小丽的证法还需要改变的大小,再进行证明,该定理的证明才完整
C.小红的证法用特殊到一般的方法证明了该定理
D.小红的证法只要将点D在的内部任意移动100次,重新测量进行验证,就能证明该定理
(3)如图,若点D在锐角外部,与相交于点G,其余条件不变,原题中结论还成立吗?若成立,请说明理由;若不成立,请探索之间的关系.
21.(2023上·山西太原·八年级校考期末)问题情境:如图1,将含 角的三角板 和含角的三角板 叠放在一起,使直角顶点重合,点 D 落在直线 上,点 E 落在直线 上. 绕点 A 旋转, 边 与 、 分别相交与点 F、点N,边 与 相交于点 M.
(1)如图 2,当 时:
①求的度数.
②判断 与的数量关系,并说明理由.
(2)如图 3,当 平分 时:
①求的度数;
②判断 与 的位置关系,并说明理由.
22.(2023上·山西太原·八年级校考期末)如图,若,垂直为点 D,,,试判断直线与 的位置关系,并说明理由.
参考答案:
1.D
【分析】直接根据三角形的稳定性解答即可.
【详解】解:A、B、C选项中都有四边形,只有D选项中只有三角形,
根据四边形的不稳定性和三角形的稳定性可知:D选项的图形具有稳定性.
故选:D.
【点睛】本题主要考查了三角形的稳定性,掌握组成的所有的图形都是三角形,则具有稳定性是解答本题的关键.
2.C
【分析】根据平行线性质和三角形内角和定理即可求解.
【详解】A、,,,由 ,得 ,故A不符合题意;
B、,,,由 ,得 ,故B不符合题意;
C、,,,无法证得三角形的内角和等于,故C符合题意;
D、如图,,,,,,,,故D不符合题意.
故选:C.
【点睛】本题考查了三角形内角和定理和平行线的性质的知识点,熟悉以上知识点是解题关键.
3.A
【分析】根据三角板得到,,再根据平行线的性质得到,最后利用三角形内角和定理计算即可.
【详解】解:如图,和交于点G,
由三角板可知:,,
∵,
∴,
∴,
故选A.
【点睛】本题考查平行线的性质,三角板的性质,三角形内角和,解题关键是结合图形利用平行线的性质进行角的转化和计算.
4.A
【分析】分别从是锐角三角形与钝角三角形去分析求解即可求得答案.
【详解】解:如图(1),当是锐角三角形时,
,,
,
,
;
如图(2),当是钝角三角形时,
,,
,
,
,;
综上所述,它的顶角度数为:或,
故选:A.
【点睛】此题考查了等腰三角形的性质,三角形内角和定理,采用分类讨论的思想是解此题的关键.
5.C
【分析】根据三角形内角和定理可得,从而得到,再由三角形外角的性质,即可求解.
【详解】解:∵,
∴,
∵的角平分线相交于点O,
∴,
∴.
故选C.
【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,熟练掌握三角形内角和定理,三角形外角的性质是解题的关键.
6.B
【分析】根据三角形外角的性质,平行线的判定,定理与逆定理,逐一进行判断即可.
【详解】解A.三角形的外角等于与它不相邻的两个内角的和,原说法错误,不符合题意;
B.内错角相等,两直线平行,是真命题,符合题意;
C.一个定理的逆命题是真命题,逆命题就是这个定理的逆定理,原说法错误,不符合题意;
D.三角形的一个外角大于任何一个与它不相邻的内角,原说法错误,不符合题意;
故选B.
【点睛】本题考查命题的真假.熟练掌握三角形外角的性质,平行线的判定,定理与逆定理,是解题的关键.
7.D
【分析】由三角形外角的性质可得、、和之间大小关系,即可得到答案.
【详解】解:是的外角,
,,
故①正确;
是的外角,
,
故②③正确;
综上,①②③正确;
故选:D.
【点睛】本题考查了三角形外角的性质,熟练掌握三角形的外角大于不相邻的每一个内角是解题的关键.
8.B
【分析】根据三角形的外角定理即可求解.
【详解】解:∵,,
∴,
故选:B.
【点睛】本题主要考查了三角形的外角定理,解题的关键是掌握三角形的一个外角等于与它不相邻的两个内角之和.
9.B
【分析】直接利用多边形的外角和为即可得出答案.
【详解】解:∵多边形的外角和为,
∴.
故选:B.
【点睛】本题考查了多边形的外角和,熟知多边形的外角和是是解题关键.
10.B
【分析】根据多边形内角和公式列出方程,求出的值,即可求出多边形的边数,再根据多边形的外角和是,利用除以边数可得外角度数.
【详解】解:根据题意,可得,
解得,
所以,外角的度数为.
故选:B.
【点睛】此题主要考查了多边形的内角与外角,解题关键是根据多边形的内角和公式和多边形的外角和为进行解答.
11.C
【分析】根据多边形的内角和公式:多边形的内角和=和正多边形的性质即可求解.
【详解】解:∵正六边形的内角和为:,
又∵正六边形的6个内角都相等,
∴它的每一个内角=.
故选C.
【点睛】本题考查多边形的内角和公式和正多边形的性质.掌握多边形的内角和=与正多边形的每一个内角都相等是解题关键.
12.4
【分析】根据图形可知三角形的面积等于三角形的面积加上三角形的面积,根据面积公式变形计算即可.
【详解】解:∵,
又∵,
,
∴,
∵,
,
,
故答案为:4.
【点睛】本题考查三角形的面积公式,三角形的高,能够熟练掌握割补法求面积是解决本题的关键.
13.105
【分析】根据平行线的性质及三角形内角和定理,即可求解.
【详解】解:,,,
,
,
,
,
故答案为:105.
【点睛】本题主要考查了平行线的性质,三角形内角和定理,解题时注意:两直线平行,内错角相等.
14.
【分析】先求出六边形的内角和,问题即可得解.
【详解】六边形的内角和为:,
即:,
故答案为:.
【点睛】本题主要考查了多边形内角和的计算公式,n边形内角和为:,掌握多边形内角和的计算公式,是解答本题的关键.
15.10
【分析】根据多边形的外角和等于360度除以每次转的角度,得到转的次数,即可计算.
【详解】解:经分析,机器猫回到点,总共转了360度.
机器猫转了(次).
机器猫移动的距离是(米).
故答案为:10.
【点睛】本题主要考查多边形的外角,熟练掌握任意多边形的外角和是360度是解决本题的关键.
16.
【分析】直接根据多边形的外角和为即可得到答案.
【详解】解:根据题意可得:
外角和的度数为:,
故答案为:.
【点睛】本题考查了多边形的外角和,熟练掌握多边形的外角和为是解题的关键.
17.11
【分析】根据多边形内角和公式及外角和,即可列出方程,解方程即可求解.
【详解】解:根据题意得:,
解得,
故答案为:.
【点睛】本题考查了多边形内角和公式及外角和,熟练掌握和运用多边形内角和公式及外角和是解决本题的关键.
18.(1),
(2)
(3)成立,理由见解析
【分析】(1)利用三角形内角和定理先求得,利用角平分线的定义求得,再利用三角形的外角性质即可求解;
(2)同(1)的方法即可求解;
(3)根据角平分线的定义推出,再根据三角形的外角性质即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴,
∵是的平分线,
∴,
∴,
∴;
(2)解:∵是的平分线,
∴,
∵,,
又∵,
∴;
(3)解:成立.
理由如下:画出符合题意的图形,如图,
∵是的角平分线,
∴,
∵是的外角,
∴,
∵是的外角,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】本题考查了三角形的外角性质,角平分线的定义,熟记各图形的性质并准确识图是解题的关键.
19.(1),证明见解析
(2)
【分析】(1)根据三角形内角和定理得到,,再结合,即可得到结论;
(2)先根据三角形内角和定理和角三等分线的定义得到,,,再代入(1)中结论求解即可.
【详解】(1)解:猜想:,
证明:由题意得:,,
∵,,
∴,
∴,
∴,
∴;
(2)解:∵,、分别是、的三等分线,
∴,,,
∴.
故答案为:.
【点睛】本题主要考查了三角形内角和定理,角三等分线的定义,熟知三角形内角和为度是解题的关键.
20.(1)三角形的一个外角等于和它不相邻的两个内角的和
(2)A
(3)不成立,
【分析】(1)连接并延长至点M,根据三角形外角的性质解答即可;
(2)按照定理的证明的一般步骤,从已知出发经过量角器测量,计算,证明,即可得答案;
(3)根据三角形外角的性质得,,整理可得答案
【详解】(1)解:小丽证明过程中的“依据”是指数学定理:三角形的一个外角等于和它不相邻的两个内角的和;
(2)根据定理证明的一般步骤,从已知出发经过量角器测量,计算,证明,故A正确;
(3)不成立,
是的一个外角,
,
为的一个外角,
,
(或).
【点睛】本题考查了三角形的外角,解题的关键是掌握三角形外角的性质:三角形的一个外角等于和它不相邻的两个内角的和.
21.(1)①;②
(2)①;②
【分析】(1)①根据平行线的性质可得,再根据三角形的内角定理即可求解;②根据平行线的性质可得,再求出的度数,最后求出的度数即可;
(2)①根据角平分线的性质,先求出的度数,再求出的度数,最后根据三角形的外角定理即可求解;②根据角平分线的性质,可求出的度数,即可得到,即可得出结论.
【详解】(1)解:①∵,
∴,
∵,
∴;
②由①得,
∴,
∴,
∴.
(2)①∵ 平分,
∴,
∴,
∵,
∴;
②由①可得,
∵,
∴,
∴.
【点睛】本题主要考查了平行线的性质和判定,三角形的外角定理,角平分线的定义,解题的关键是掌握三角形的各个角的度数.
22.,理由见解析
【分析】延长交于D,依据,,即可得到,进而得出.
【详解】解:.理由:
如图,延长交于D,
∵,,
∴,
∵,
∴,
∴,
∴.
【点睛】此题主要考查了平行线的性质与判定,关键是掌握两条直线都和第三条直线平行,那么这两条直线平行.
